Похожие презентации:
Интерполяция. Определитель Вандермонда
1.
ИнтерполяцияИнтерполяция - это способ нахождения
промежуточных
значений
величины
по
имеющемуся дискретному набору известных
значений.
Интерполяция
использует
значения
некоторой функции, заданные в ряде точек,
чтобы предсказать значения функции между
ними.
2.
Перечисленныениже
методы
предназначены для создания ряда с более
высокой частотой наблюдений на основе
ряда с низкой частотой. Например,
вычислить ряд с квартальной динамикой
на основе ряда годовых данных.
3.
Предположим,что
есть
система
несовпадающих точек xi (i ϵ 0, 1, …, N) из
некоторой области G.
Значения функции f известны только в этих
точках: yi = f(xi), i = 1, …, N.
Процесс интерполяции состоит в поиске
такой функции f из заданного класса функций,
что F(xi) = yi, i = 1, …, N.
Точки xi являются узлами интерполяции, а их
совокупность - интерполяционной сеткой.
4.
Пары (xi, yi) являются точками данных (базовымиточками).
Разность между «соседними» значениями ∆xi = xi -xi - 1 называют шагом интерполяционной сетки.
Шаг может быть переменным или постоянным.
Функцию
F(x)
интерполирующей
функцией
(интерполянтой).
Линейная интерполяция
При линейной интерполяции существующие точки
данных М(xi, yi) (i = 0, 1, ..., n) соединяются прямыми
линиями и функция f(x) приближается к ломаной с
вершинами в данных точках.
Уравнения каждого отрезка ломаной линии в общем
случае разные.
5.
Поскольку имеется n интервалов (xi, xi+1), то длякаждого
из
них
в
качестве
уравнения
интерполяционного полинома используется уравнение
прямой, проходящей через две точки. В частности,
для i-го интервала можно написать уравнение прямой,
проходящей через точки (xi, yi) и (xi+1, yi+1), в виде:
6.
7.
Пусть известные значения некоторой функции fобразуют следующую таблицу.
При этом требуется получить значение функции f для
такого значения x, который входит в интервал x0, xn ,
но не совпадает ни с одним значением xi (i=0,1,…,n).
x
f(x)
x0
y0
x1
y1
x2
y2
x3
y3
…
…
…
…
xn
yn
Очевидный прием – вычислить значение функции f(x),
используя аналитического выражение функции.
8.
Особый прием – построение по исходной информацииприближающей функции F(x), которая в некотором
смысле близка к функции f(x) и аналитическим
выражением которого можно воспользоваться для
вычислений, считая приближенно, что f(x)=F(x).
(1)
Классический прием – построение приближающей
функции, основывается на требовании строгого
совпадении
значении f(x) и F(x) в точках xi , то есть
F ( x 0 ) y 0 , F ( x1 ) y1 ,..., F ( x n ) y n .
(2)
9.
В этом случае нахождение приближенной функцииназывается интерполяцией (или интерполированием),
а точки xi (i=0,1,…,n) – узлами интерполяции.
Интерполирующую функцию F(x) будем искать в виде
многочлена степени n
P n ( x) a0 x a1 x
n
n 1
a n 1 x a n
(3)
10.
Этот многочлен имеет n+1 коэффициентов. Естественнопредполагаем, что n+1 условий (2) наложенные на
многочлен, позволят однозначно определить его
коэффициенты. Действительно, требуя для многочлена
n(x) выполнение условий (2), получаем систему n+1
уравнений с n+1 неизвестными
n
a x
k 0
k
n k
i
yi
(i 0,1,..., n)
(4)
11.
Решая эту систему относительно неизвестных a 0 , a1 ,..., a n , мы и получиманалитическое выражение полинома (3). Система (4) всегда имеет
единственное решение, так как ее определитель
n n 1
x0 x0 x0 1
n 1
1
x x x1 1
n
1
n 1
n
x x xn 1
n
n
известный как определитель Вандермонда, отличен от нуля.
12.
Интерполяционный многочлен ЛагранжаПусть функция f(x) задана таблицей. Построим
интерполяционный многочлен Ln(x), степень которого не
больше n и для которого выполнены условия (2). Будем
искать многочлен Ln(x) в виде:
Ln(x)=l0(x)+l1(x)+...+ln(x)
(5),
где li(x) – многочлены степени n, причем
yi , i k
li ( xk )
0, i k
(6).
13.
Многочленыli(x)
составим
следующим
образом
l i ( x) ci ( x x 0 )( x x1 ) ( x xi 1 )( x xi 1 ) ( x x n )
(7),
Где сi – постоянный коэффициент, значение которого находим из первой части
yi
ci
условия (6)
. Подставим
( xi x 0 ) ( x xi 1 )( xi xi 1 ) ( x x n )
значение сi в условие (7), получим
14.
yil i ( x)
( x x 0 ) ( x x n ) и с учетом
( x i x 0 ) ( x i x i 1 )( x i x i 1 ) ( x i x n )
(5), окончательно имеем
n
( x x 0 ) ( x x i 1 )( x x i 1 ) ( x x n )
Ln ( x) y i
(8)
i 0
( x i x 0 ) ( x i x i 1 )( x i x i 1 ) ( x i x n )
Используя обозначение
n 1 ( x) ( x x0 )( x x1 ) ( x xn ) формуле Лагранжа можно придать более
сжатый вид. Продифференцируем n 1 ( x) по x :
15.
n( x) ( x x0 ) ( x xi 1 )( x xi 1 ) ( x xn ) при x xi (i 0,1,...,n)
'
n 1
i 0
n
( x) ( xi x0 ) ( xi xi 1 )( xi xi 1 ) ( xi xn ) следовательно
'
n 1
i 0
yi
Ln ( x) n 1 ( x)
.
'
i 0 ( x xi ) n 1 ( xi )
n
16.
x x0 x0 x1 x0 xnx1 x0 x x1 x1 xn
D
произведение
элементов
строк
(i=0,1,…,n).
i
x x x x x x
n 0 n 1
n
n 1 ( x) - произведение элементов главной диагонали.
n
yi
Ln ( x) n 1 ( x) .
i 0 Di
17.
Пример: Пусть дана таблицаx
1
3
4
f(x) 12 4
6
Построите многочлен Лагранжа. Для решения используем формулу (8),
получаем
n 2 x0 1, x1 3, x2 4
( x 3)( x 4) ( x 1)( x 4) ( x 1)( x 3)
2
L2 ( x) 12
4
6
2 x 12 x 22
(1 3)(1 4) (3 1)(3 4) (4 1)(4 3)














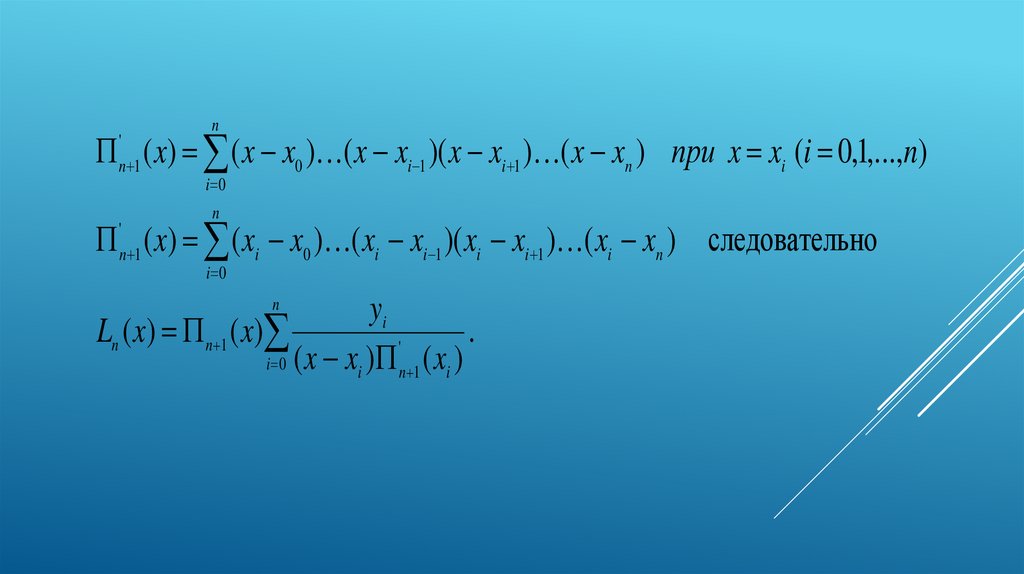


 Математика
Математика








