Похожие презентации:
Подобие треугольников
1.
2.
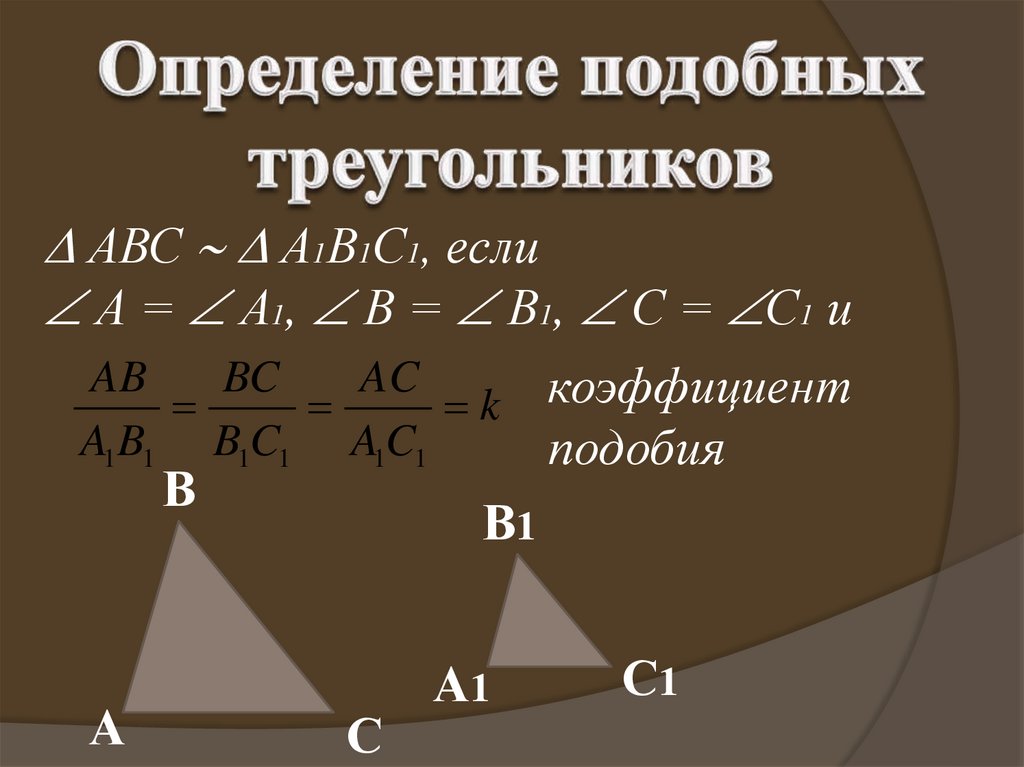
АВС А1В1С1, еслиА = А1, В = В1, С = С1 и
AB
BC
AC
k
A1 B1 B1C1 A1C1
В
А
коэффициент
подобия
В1
С
А1
С1
3.
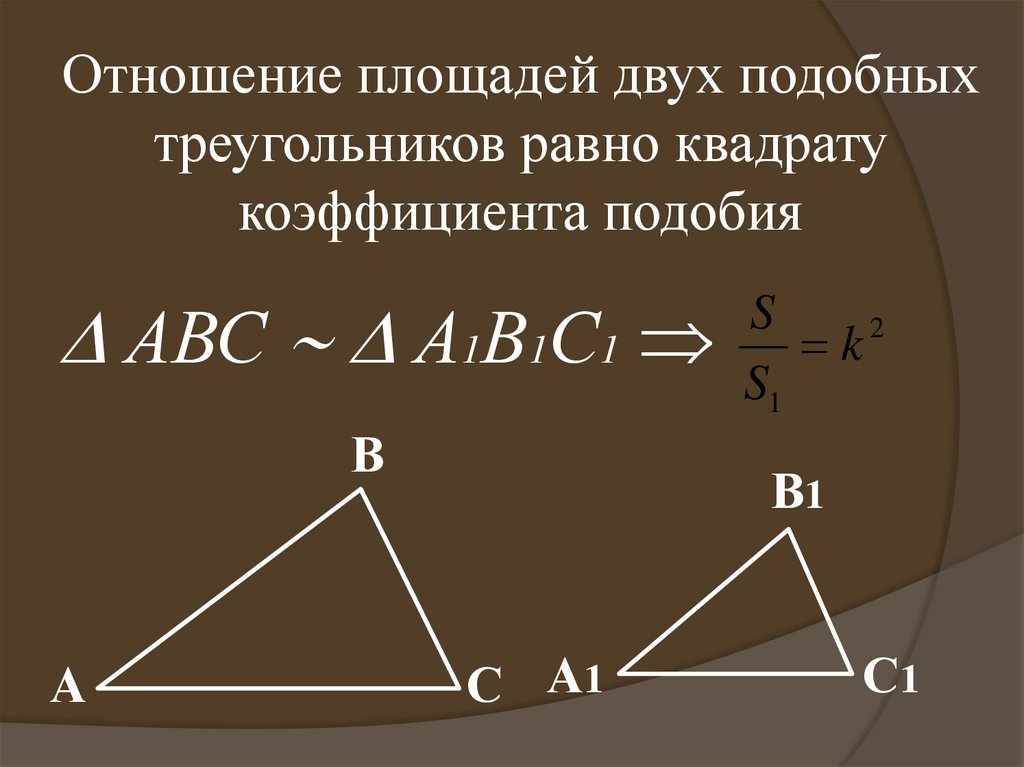
Отношение площадей двух подобныхтреугольников равно квадрату
коэффициента подобия
АВС
S
2
А1 В1 С 1 S k
1
В
А
В1
С А1
С1
4.
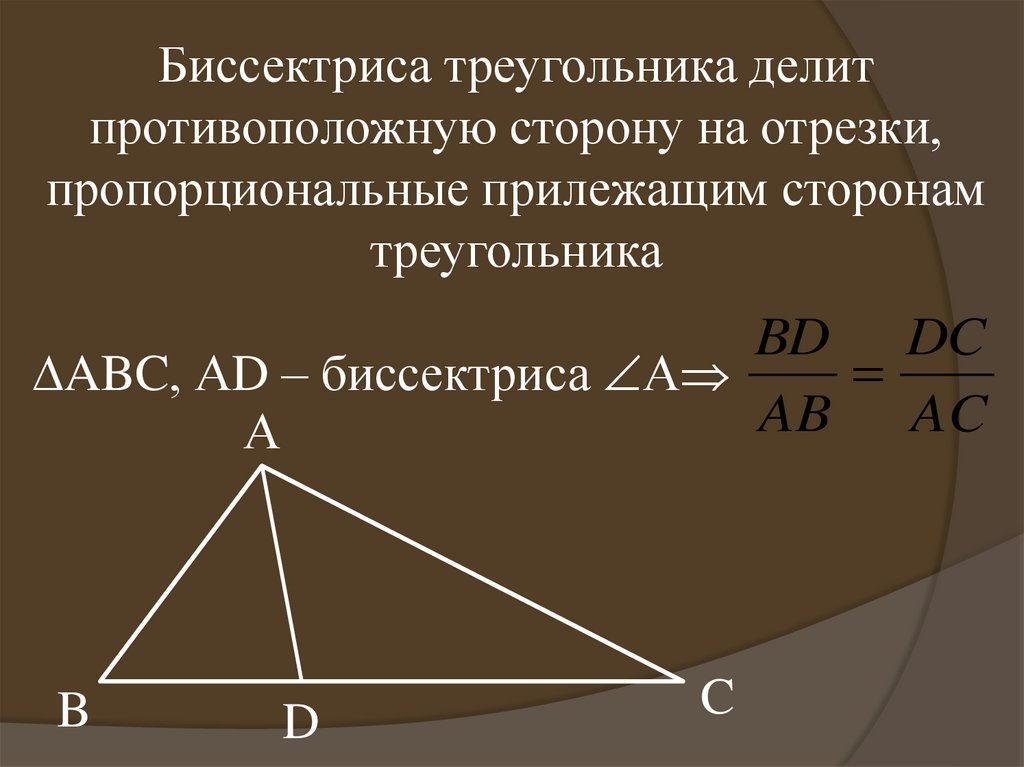
Биссектриса треугольника делитпротивоположную сторону на отрезки,
пропорциональные прилежащим сторонам
треугольника
BD DC
ABC, АD – биссектриса А
AB AC
А
B
D
C
5.
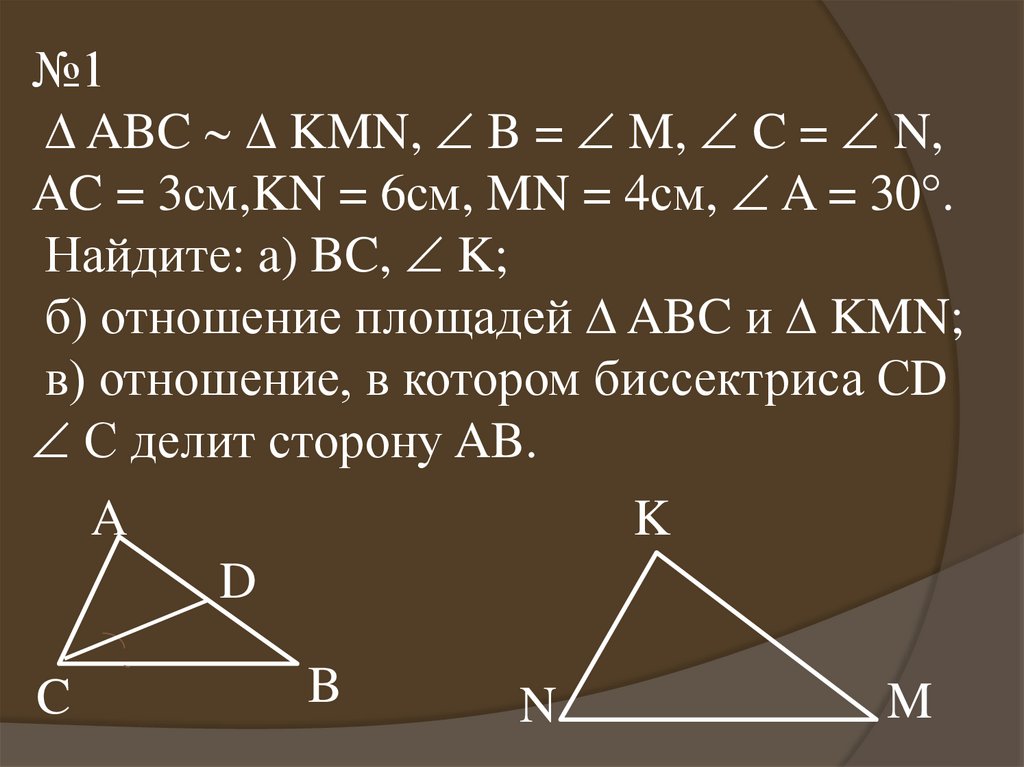
№1ABC KMN, B = M, C = N,
AC = 3см,KN = 6см, MN = 4см, A = 30°.
Найдите: a) BC, K;
б) отношение площадей ABC и KMN;
в) отношение, в котором биссектриса СD
С делит сторону AB.
A
K
D
C
B
N
M
6.
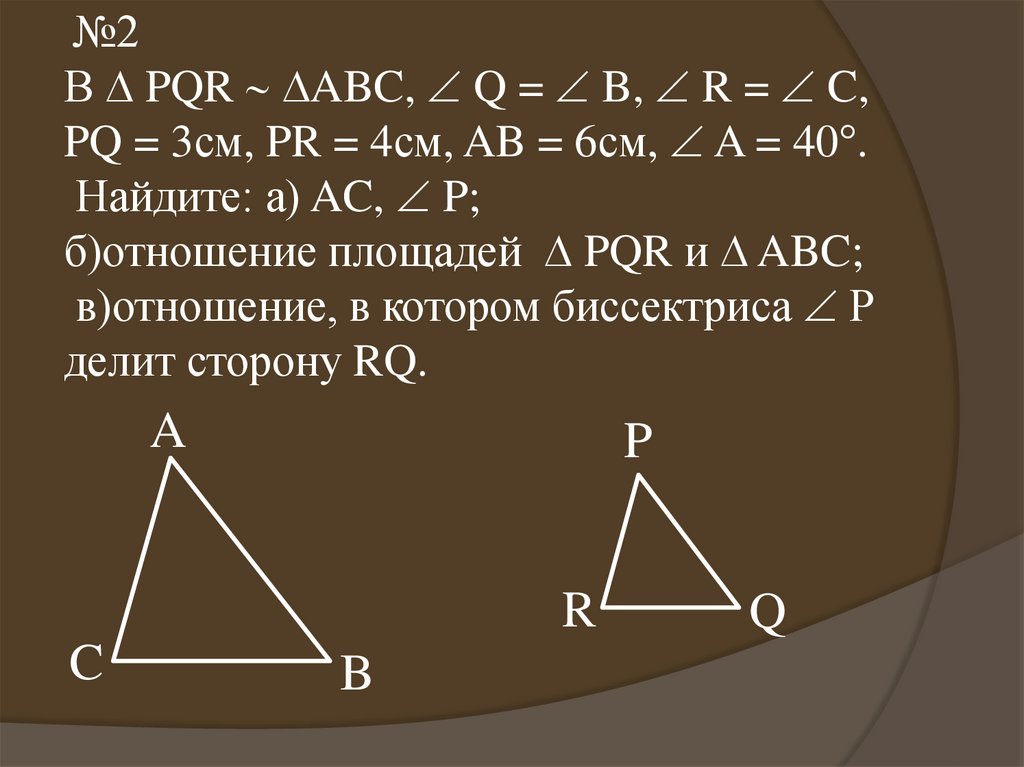
№2В PQR ABC, Q = B, R = C,
PQ = 3см, PR = 4см, AB = 6см, A = 40°.
Найдите: а) AC, P;
б)отношение площадей PQR и ABC;
в)отношение, в котором биссектриса Р
делит сторону RQ.
A
P
R
C
B
Q
7.
№ 332 (а)Стороны треугольника равны 2,5 см, 4 см,
5 см. Найдите стороны треугольника,
подобного данному, если его периметр
равен 46 см.
8.
По двумсторонам и углу
между ними
По двум
углам
По трем
сторонам
9.
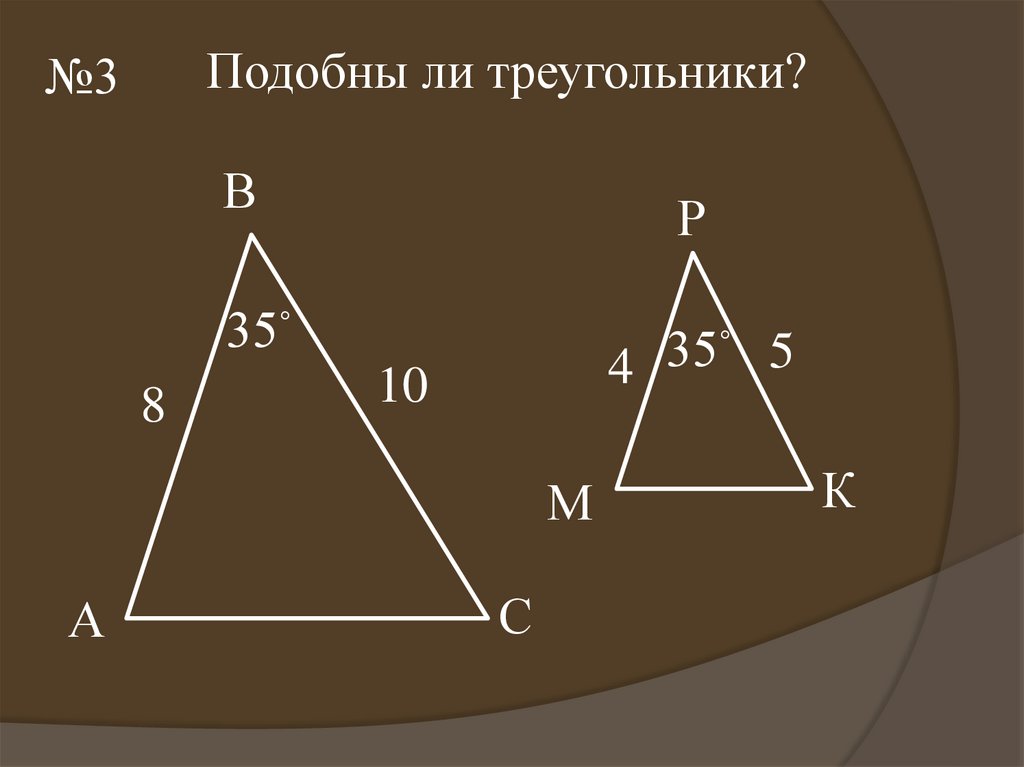
Подобны ли треугольники?№3
В
Р
35˚
8
4 35˚ 5
10
М
А
С
К
10.
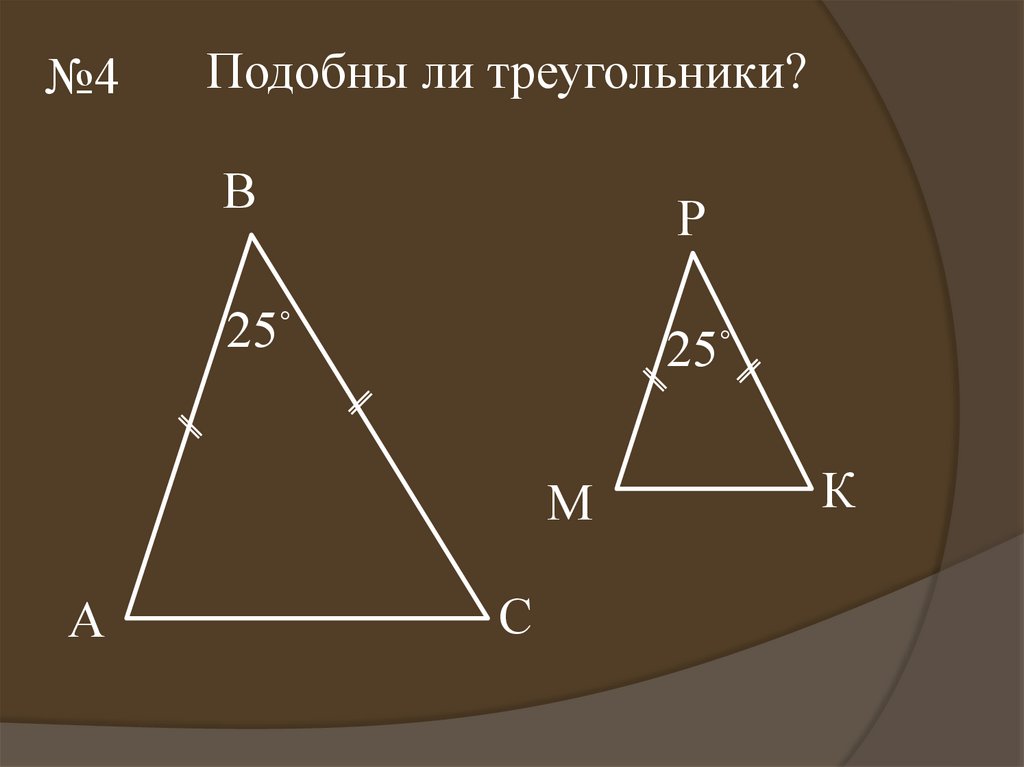
№4Подобны ли треугольники?
В
Р
25˚
25˚
М
А
С
К
11.
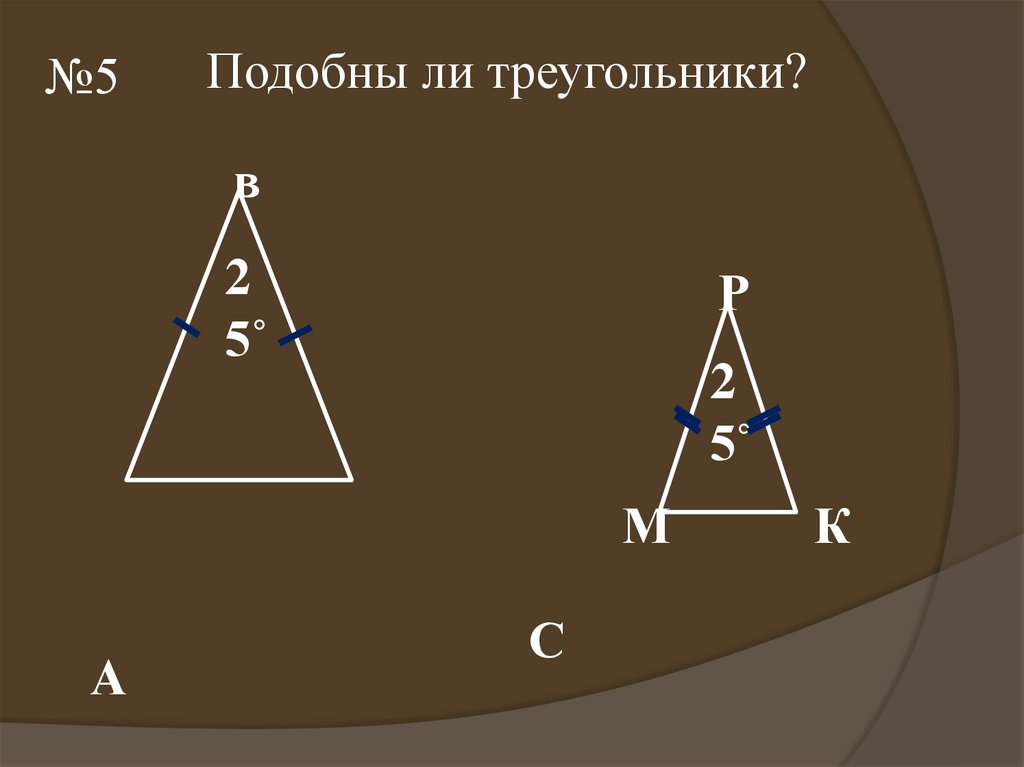
№5Подобны ли треугольники?
в
2
5˚
Р
2
5˚
М
А
С
К
12.
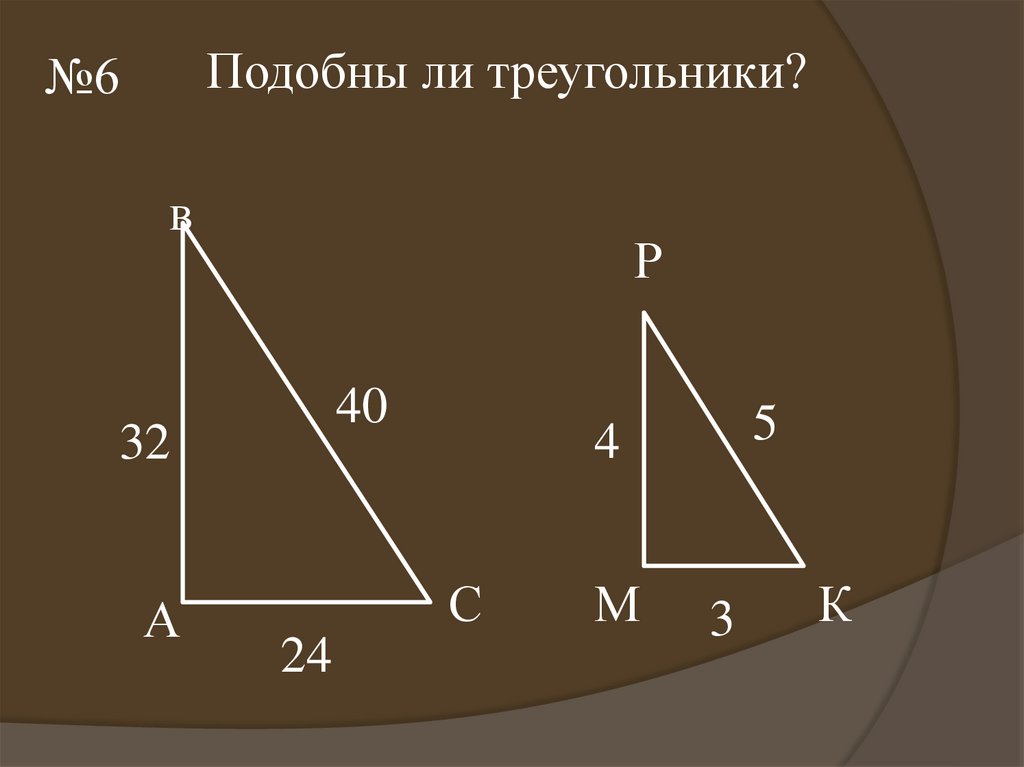
Подобны ли треугольники?№6
в
Р
40
32
А
С
24
5
4
М
3
К
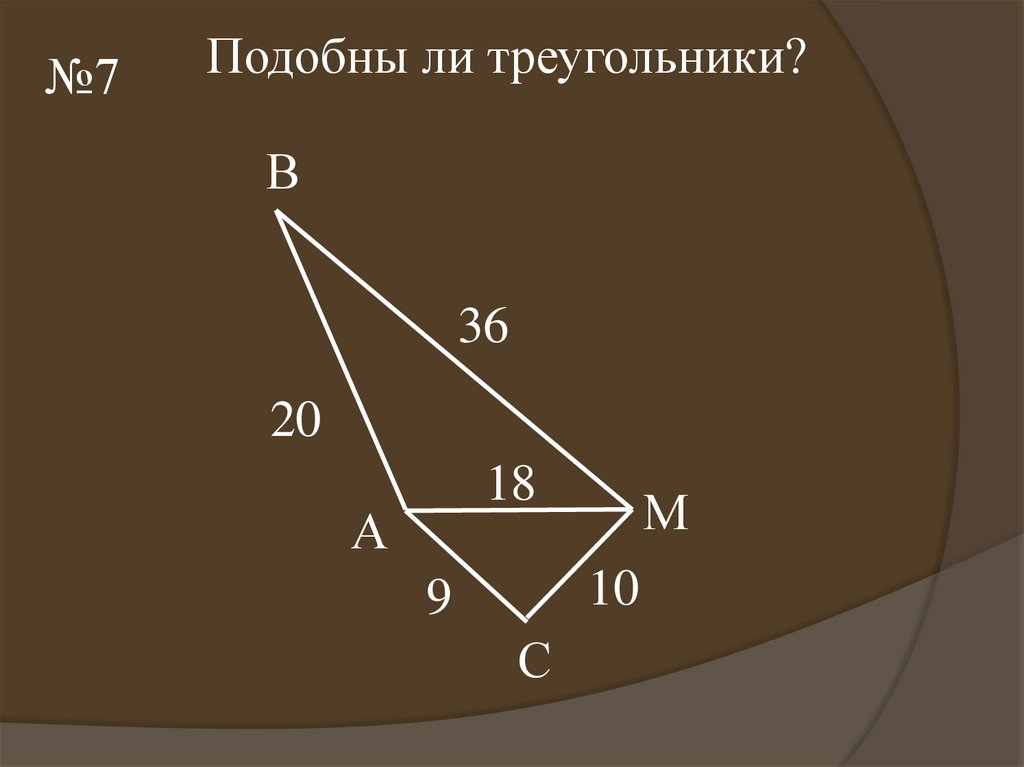
13.
№7Подобны ли треугольники?
В
36
20
18
А
М
10
9
С
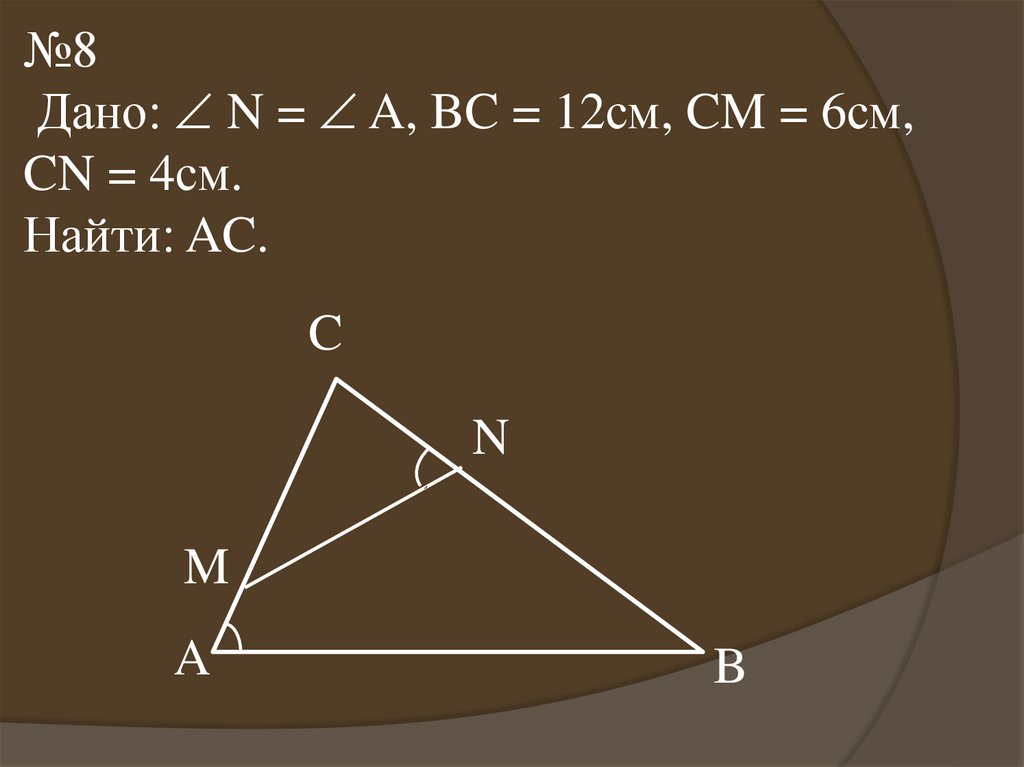
14.
№8Дано: N = A, BC = 12см, CM = 6см,
CN = 4см.
Найти: AC.
C
N
M
A
B
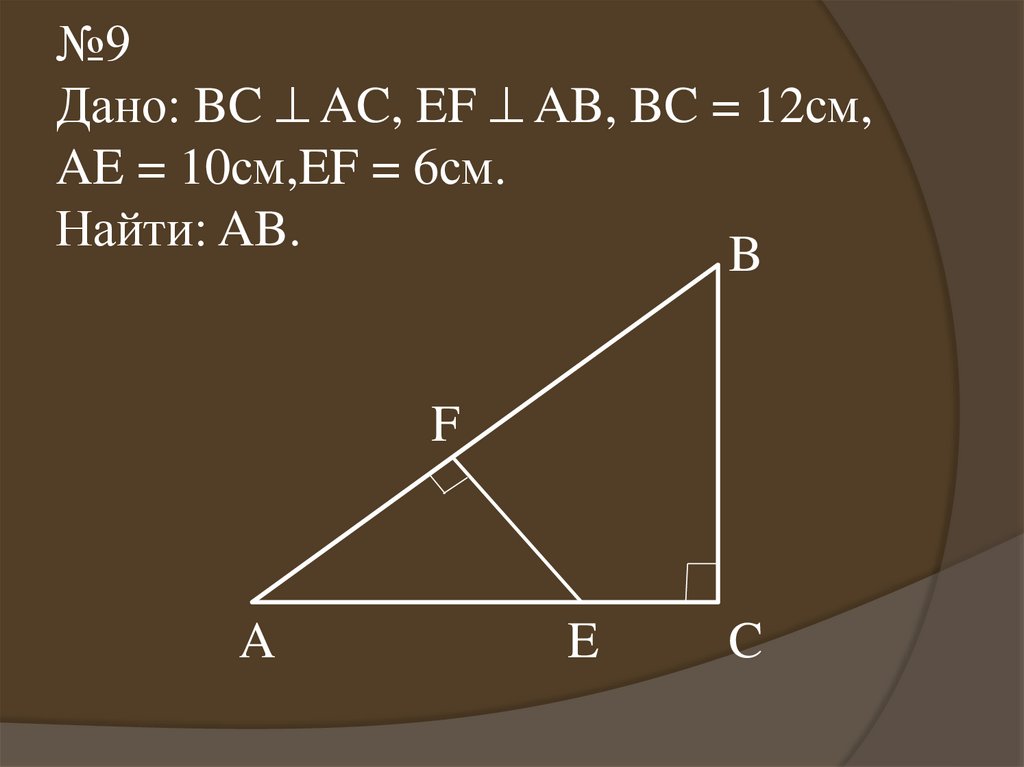
15.
№9Дано: BC AC, EF AB, BC = 12см,
AE = 10см,EF = 6см.
Найти: AB.
B
F
A
E
C
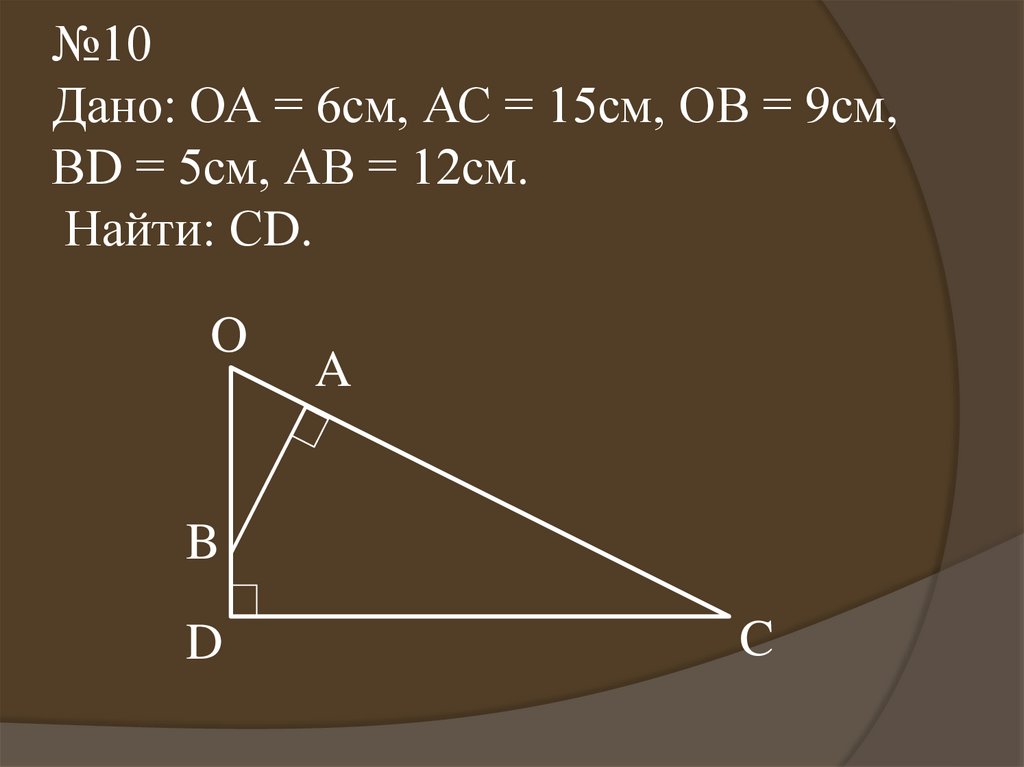
16.
№10Дано: ОА = 6см, АС = 15см, ОВ = 9см,
ВD = 5см, АВ = 12см.
Найти: СD.
O
A
B
D
C
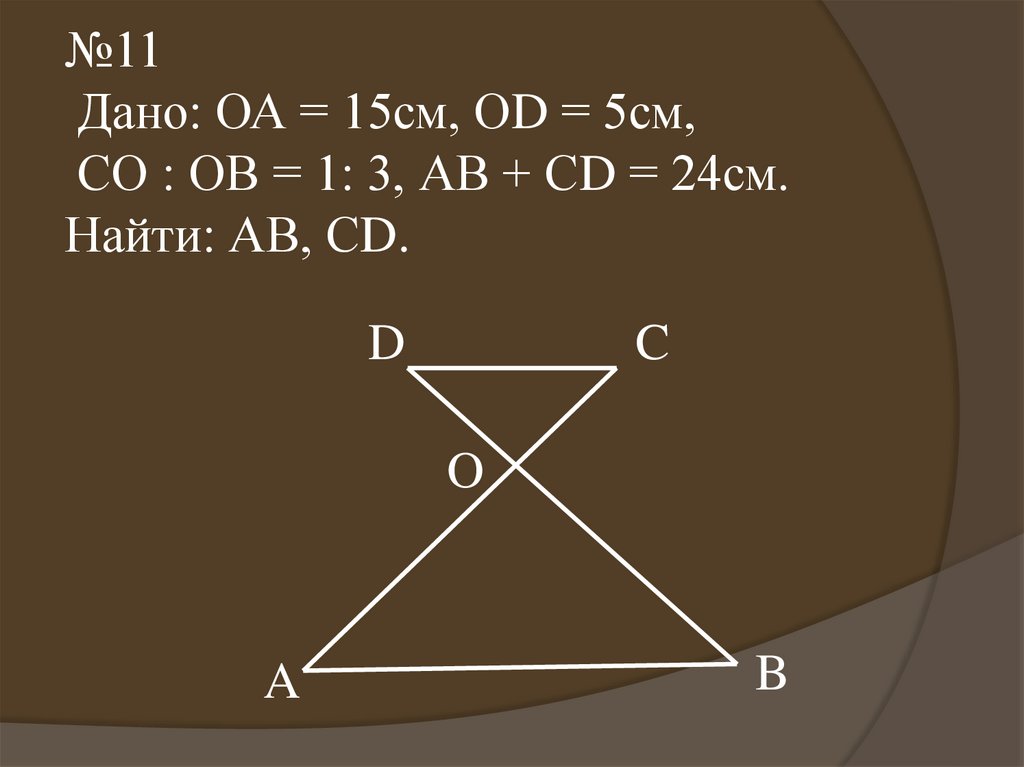
17.
№11Дано: ОА = 15см, ОD = 5см,
СО : ОВ = 1: 3, АВ + СD = 24см.
Найти: АВ, СD.
D
C
O
A
B
18.
№ 551(б)На стороне СD параллелограмма ABCD
отмечена точка Е. Прямые АЕ и ВС
пересекаются в точке F. Найдите DЕ и ЕС,
если АВ = 8 см, AD = 5см, CF = 2см
19.
№554В
М
5
С
3,9
3,6
А
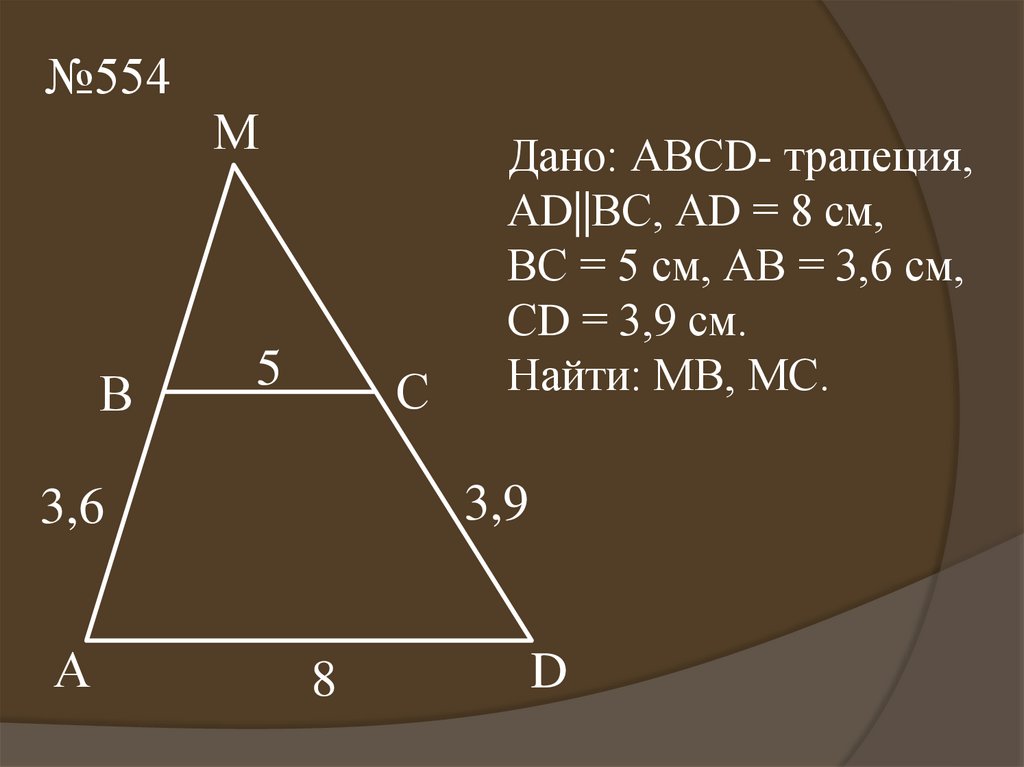
Дано: АВСD- трапеция,
АD||ВС, АD = 8 см,
ВС = 5 см, АВ = 3,6 см,
СD = 3,9 см.
Найти: МВ, МС.
8
D




 Математика
Математика








