Похожие презентации:
Примеры применения теории Онзагера
1.
ПРИМЕРЫ ПРМЕНЕНИЯ ТЕОРИИОНЗАГЕРА
2.
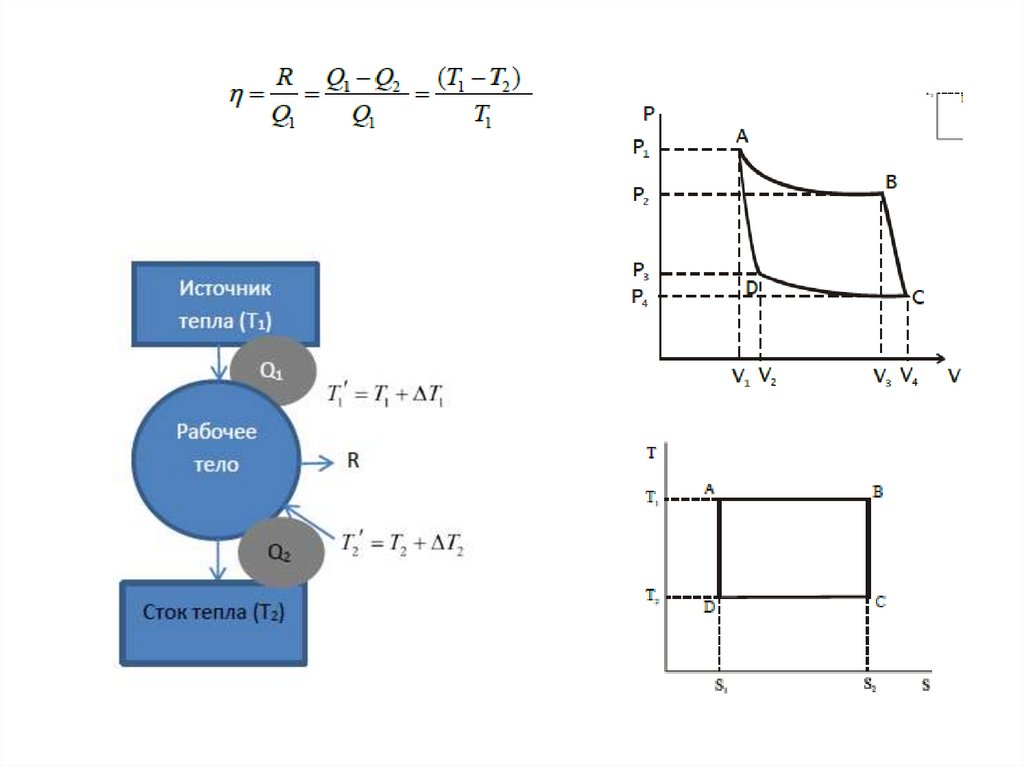
Формула Курзона и АльборнаСкорость генерации энтропии, некомпенсированной обменом
тепла между тепловым резервуаром и рабочим телом, в будет
определяется разностью между скоростью прибыли энтропии
рабочего тела:
di SQ
dt
dSin dSout dQ 1 1
J QYQ
dt
dt
dt T T0
dQ
JQ
T0 T
dt
di SW dWlost P P0 dV
YW JW
dt
dt
T
dt
dV
JW
P P0
dt
JQ
dQ
dt
1 1
YQ
T T
1 1
T T 0
T0 T 0
dt
T0T
T T0
2
d i SQ
YW
P P0
dV
; JW
T
dt
P P0 0
di SW
dt
T
2
3.
4.
Разность температур между тепловым резервуаром и рабочим телом при постояннойтемпературе последнего может вызывать не только поток тепла, но и движение
поршня (расширение рабочего тела). Точно также сила, приложенная к поршню,
вызывает не только изменение объёма рабочего тела, но и тепловой поток от рабочего
тела к тепловому резервуару.
dQ
JQ
T T P P0 YQ YW
dt
dW
JW
P P0 (T T ) YW YQ
dt
полная скорость генерации энтропии представляется в виде:
di S di SQ di SW
J QYQ JWYW YQ2 2 YQYW YW2 0
dt
dt
dt
Мощность машины Карно зависит от соответствующих разностей температур
рабочего тела, нагревалеля и холодильника
W ( T1 , T0 ) Q1 Q0
dW
0;
d ( T1 )
dW
0
d ( T0 )
CA 1
T0
T1
; Wmax
T1 T0
2
5.
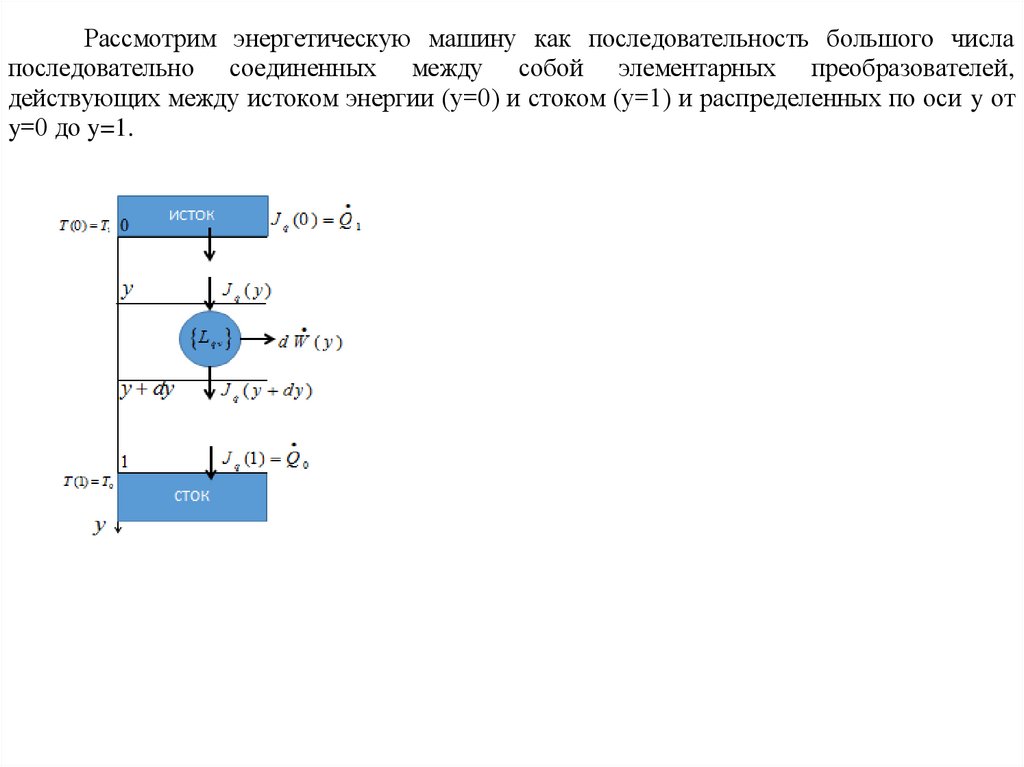
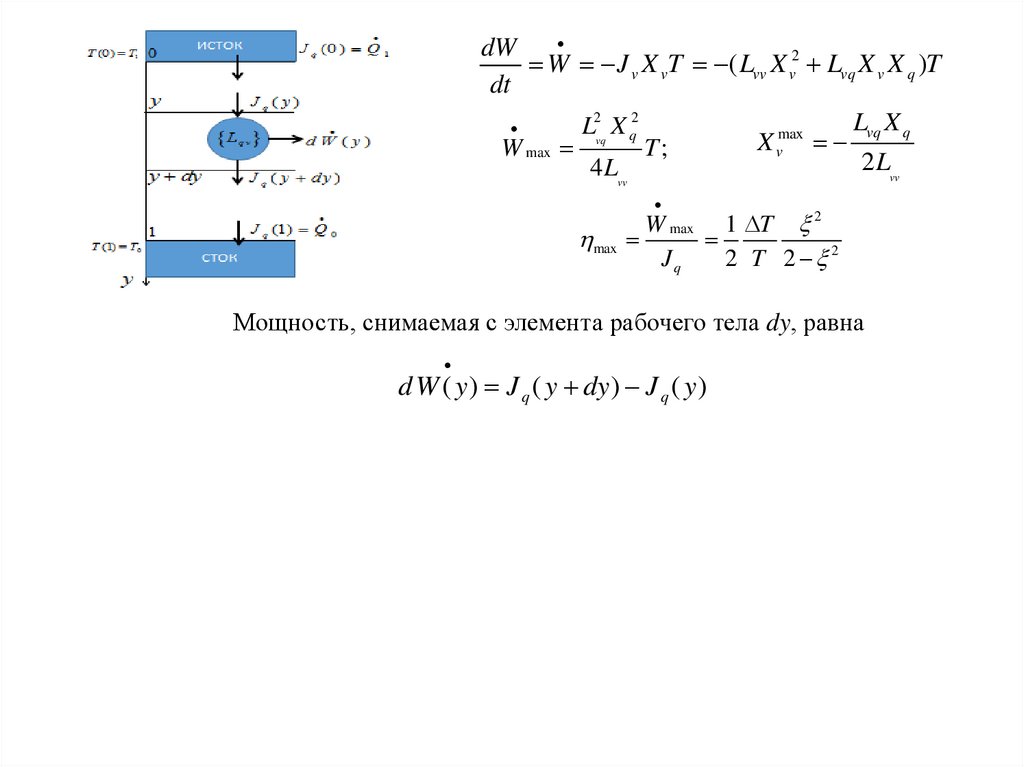
Рассмотрим энергетическую машину как последовательность большого числапоследовательно соединенных между собой элементарных преобразователей,
действующих между истоком энергии (у=0) и стоком (у=1) и распределенных по оси y от
y=0 до y=1.
6.
Рассмотрим энергетическую машину как последовательность большого числапоследовательно соединенных между собой элементарных преобразователей,
действующих между истоком энергии (у=0) и стоком (у=1) и распределенных по оси y от
y=0 до y=1.
Пусть J q -входящий поток энергии (например, тепловой J q Q ) и J - исходящий поток, в
качестве которого может быть изменение объема J V рабочего тела, выполняющего
механическую работу. В соответствии с теорией Онсагера, потоки связаны линейным
соотношением с термодинамическими силами.
J q Lqq X q Lqv X v
J v Lvq X q Lvv X v
7.
Рассмотрим энергетическую машину как последовательность большого числапоследовательно соединенных между собой элементарных преобразователей,
действующих между истоком энергии (у=0) и стоком (у=1) и распределенных по оси y от
y=0 до y=1.
Пусть J q -входящий поток энергии (например, тепловой J q Q ) и J - исходящий поток, в
качестве которого может быть изменение объема J V рабочего тела, выполняющего
механическую работу. В соответствии с теорией Онсагера, потоки связаны линейным
соотношением с термодинамическими силами.
J q Lqq X q Lqv X v
J v Lvq X q Lvv X v
В случае преобразования тепла в механическую работу X q T , X F , где F –
внешняя сила, против которой совершается работа W, а Lij -кинетические коэффициенты
Онсагера, удовлетворяющие следующим условиям:
Lqq 0; Lvv 0; Lvq Lqv ;
8.
Рассмотрим энергетическую машину как последовательность большого числапоследовательно соединенных между собой элементарных преобразователей,
действующих между истоком энергии (у=0) и стоком (у=1) и распределенных по оси y от
y=0 до y=1.
Пусть J q -входящий поток энергии (например, тепловой J q Q ) и J - исходящий поток, в
качестве которого может быть изменение объема J V рабочего тела, выполняющего
механическую работу. В соответствии с теорией Онсагера, потоки связаны линейным
соотношением с термодинамическими силами.
J q Lqq X q Lqv X v
J v Lvq X q Lvv X v
В случае преобразования тепла в механическую работу X q T , X F , где F –
внешняя сила, против которой совершается работа W, а Lij -кинетические коэффициенты
Онсагера, удовлетворяющие следующим условиям:
Lqq 0; Lvv 0; Lvq Lqv ;
Lqq Lvv L2qv 0; q 2
L2qv
Lqq Lvv
1
9.
Рассмотрим энергетическую машину как последовательность большого числапоследовательно соединенных между собой элементарных преобразователей,
действующих между истоком энергии (у=0) и стоком (у=1) и распределенных по оси y от
y=0 до y=1.
Пусть J q -входящий поток энергии (например, тепловой J q Q ) и J - исходящий поток, в
качестве которого может быть изменение объема J V рабочего тела, выполняющего
механическую работу. В соответствии с теорией Онсагера, потоки связаны линейным
соотношением с термодинамическими силами.
J q Lqq X q Lqv X v
J v Lvq X q Lvv X v
В случае преобразования тепла в механическую работу X q T , X F , где F –
внешняя сила, против которой совершается работа W, а Lij -кинетические коэффициенты
Онсагера, удовлетворяющие следующим условиям:
Lqq 0; Lvv 0; Lvq Lqv ;
Lq q Lvv L2qv 0; 2
L2qv
Lq q Lvv
1
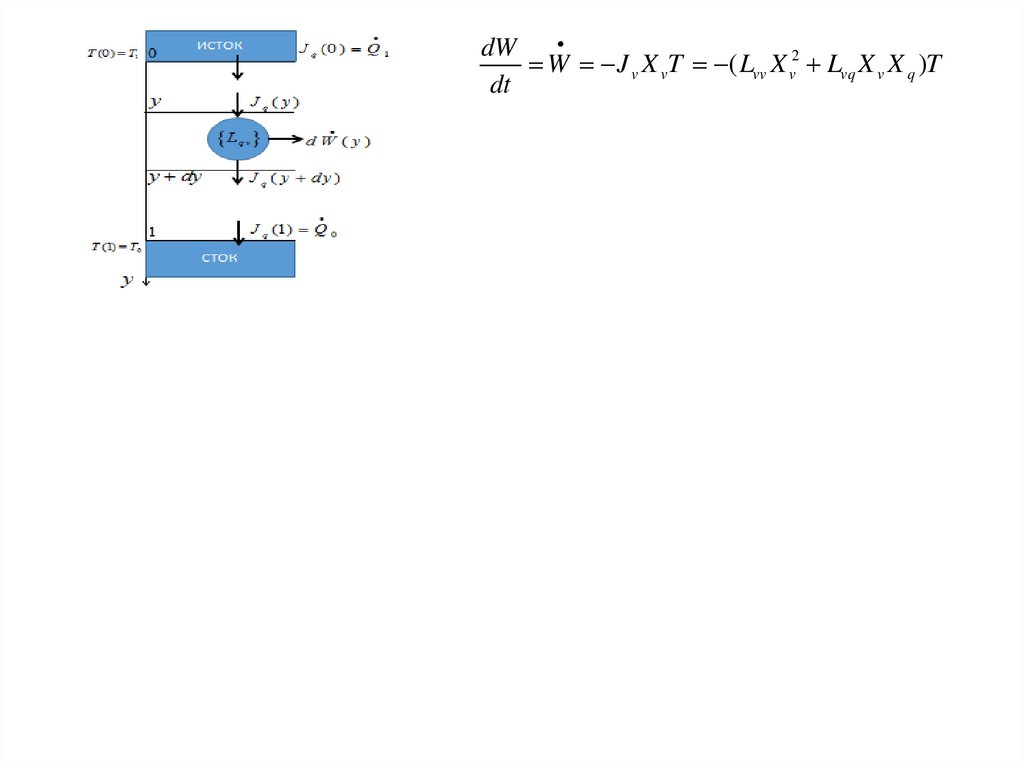
Мощность преобразования энергии представляется в виде
dW
W J v X vT ( Lvv X v2 Lvq X v X q )T
dt
10.
dWW J v X vT ( Lvv X v2 Lvq X v X q )T
dt
11.
dWW J v X vT ( Lvv X v2 Lvq X v X q )T
dt
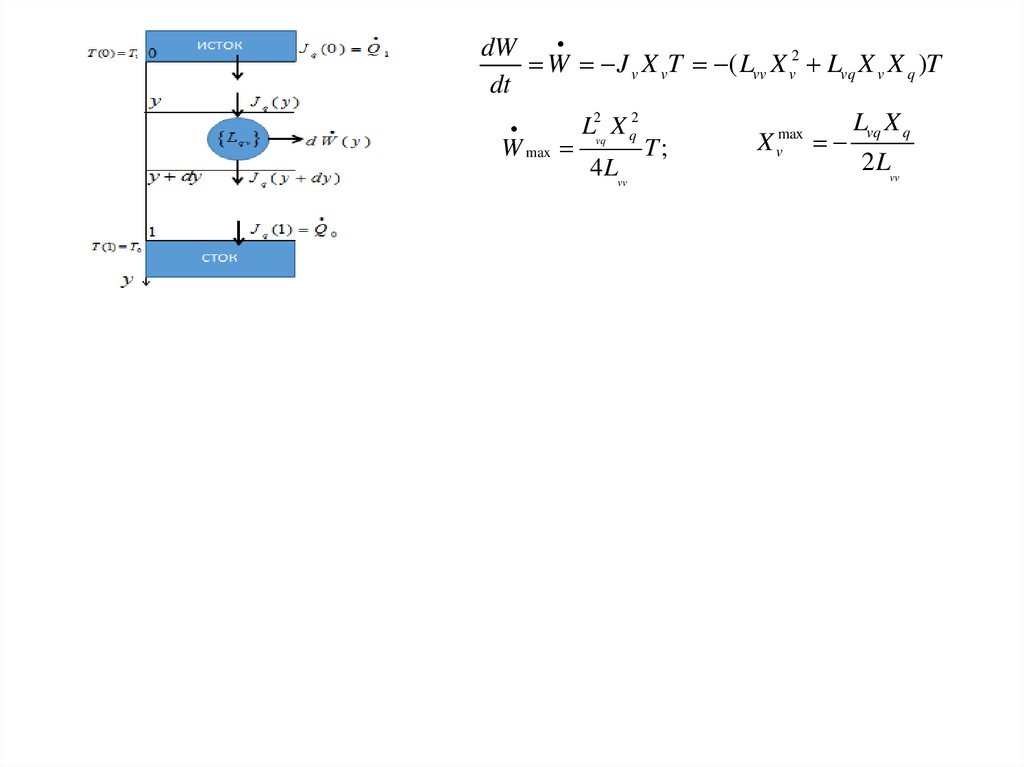
Lvq X q
L2 X q2
max
X
W max
T;
v
2 Lvv
4L
vq
vv
12.
dWW J v X vT ( Lvv X v2 Lvq X v X q )T
dt
Lvq X q
L2 X q2
max
X
W max
T;
v
2 Lvv
4L
vq
vv
W max 1 T 2
max
Jq
2 T 2 2
Мощность, снимаемая с элемента рабочего тела dy, равна
d W ( y ) J q ( y dy ) J q ( y )
13.
dWW J v X vT ( Lvv X v2 Lvq X v X q )T
dt
Lvq X q
L2 X q2
max
X
W max
T;
v
2 Lvv
4L
vq
vv
W max 1 T q 2
max
Jq
2 T 2 q2
Мощность, снимаемая с элемента рабочего тела dy, равна
d W ( y ) J q ( y dy ) J q ( y )
Интегрируя это выражение по y
y
J q ( y ) J q (0) d W ( y )
0
Приходим к следующему выражению для КПД.
T
T1
(W Wmax ) 1 0
2
2(2 2 )
,
L12
L11 L22
При 1 приходим к формуле Курзона-Альборна. Более подробный вывод можно
посмотреть в оригинальной работе Ван-дер-Броека.















 Физика
Физика








