Lektsia_10_Uravnenie_pryamoy_na_ploskosti

1. Прямая на плоскости

Общее уравнение прямой
Уравнение прямой в отрезках
Параметрическое уравнение прямой
Векторное уравнение прямой
Каноническое уравнение прямой
Нормальное уравнение прямой
Уравнение прямой с угловым коэффициентом
Угол между двумя прямыми
Расстояние от точки до прямой
Биссектриса углов между прямыми

2.

Кривые, которые в заданной прямоугольной системе
координат описываются алгебраическим
уравнением первого порядка Ах+Ву+С=0 , где хотя
бы один из коэффициентов А или В отличен от нуля,
называются алгебраическими кривыми первого
порядка. А само уравнение - линейным
уравнением.
Теорема
Любая прямая на плоскости представляет
собой алгебраическую кривую первого порядка
и любая алгебраическая кривая первого
порядка на плоскости есть прямая.

3. Общее уравнение прямой

Уравнение вида:
Ax By C 0
с произвольными коэффициентами А; В; С такими , что А и В не
равны нулю одновременно, называется общим уравнением
прямой.
М0(х0; у0 )
Теорема
Если точка М0(х0; у0 ) принадлежит прямой, то
общее уравнение прямой превращается в
тождество: Ax0 By 0 C 0
Пусть задана прямая: Ax By C 0
Вектор n
A; B будет ортогонален этой прямой.
Доказательство:
Пусть некоторая точка М0(х0; у0 ) принадлежит прямой:
Ax0 By 0 C 0
(2)
(1)

4. Общее уравнение прямой

Найдем разность уравнений (1) и (2):
Ax By C 0
Ax0 By 0 C 0
n
М (х; у )
М0(х0; у0 )
A x x0 B y y 0 0 (3)
Пусть точки М0(х0; у0 ) и М (х; у ) лежат на данной прямой.
Рассмотрим векторы: n
A; B и M M x x ; y y
0
0
0
Равенство (3) представляет собой скалярное произведение этих
векторов, которое равно нулю:
n M0M 0
n M0 M
Таким образом, вектор n перпендикулярен прямой и называется
нормальным вектором прямой.
Равенство (3) также является уравнением
прямой,проходящей через точку перпендикулярно вектору

5.

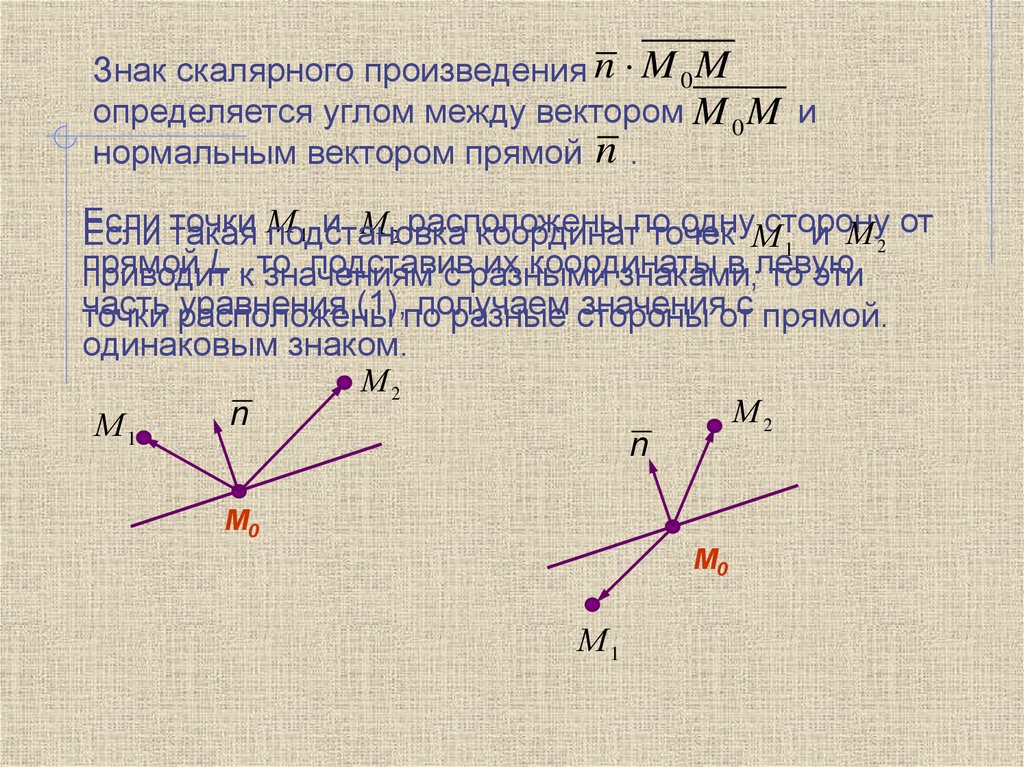
Знак скалярного произведения n M 0 M
определяется углом между вектором M 0 M и
нормальным вектором прямой n .
М 1 и М 2 расположены
Если
точки подстановка
однуМсторону
от
М
Если такая
координатпо
точек
и
2
1
прямой
L
,
то,
подставив
их
координаты
в
левую
приводит к значениям с разными знаками, то эти
часть
уравнения (1),по
получаем
значенияотс прямой.
точки расположены
разные стороны
одинаковым знаком.
М2
М2
n
М1
n
М0
М0
М1

6.

Пример
Выяснить, как по отношению к прямой
расположены точки А (4;4) и В (6;6)
Подставив координаты точки А в левую часть
общего уравнения прямой, получим
положительное число 1, а подстановка координат
точки В приводит к отрицательному числу -1.
Значит, точки А и В расположены по разные
стороны от данной прямой.

7. Исследование общего уравнения прямой

Общее уравнение прямой называется полным, если все
коэффициенты А, В, и С отличны от нуля.
В противном случае уравнение называется неполным.
Виды неполных уравнений:
A
1) C 0 Ax By 0 y x
B
C
2) B 0 Ax C 0 x
A
C
3) A 0 By C 0 y
B
4) B C 0 Ax 0 x 0
5) A C 0 By 0 y 0
y
0
х

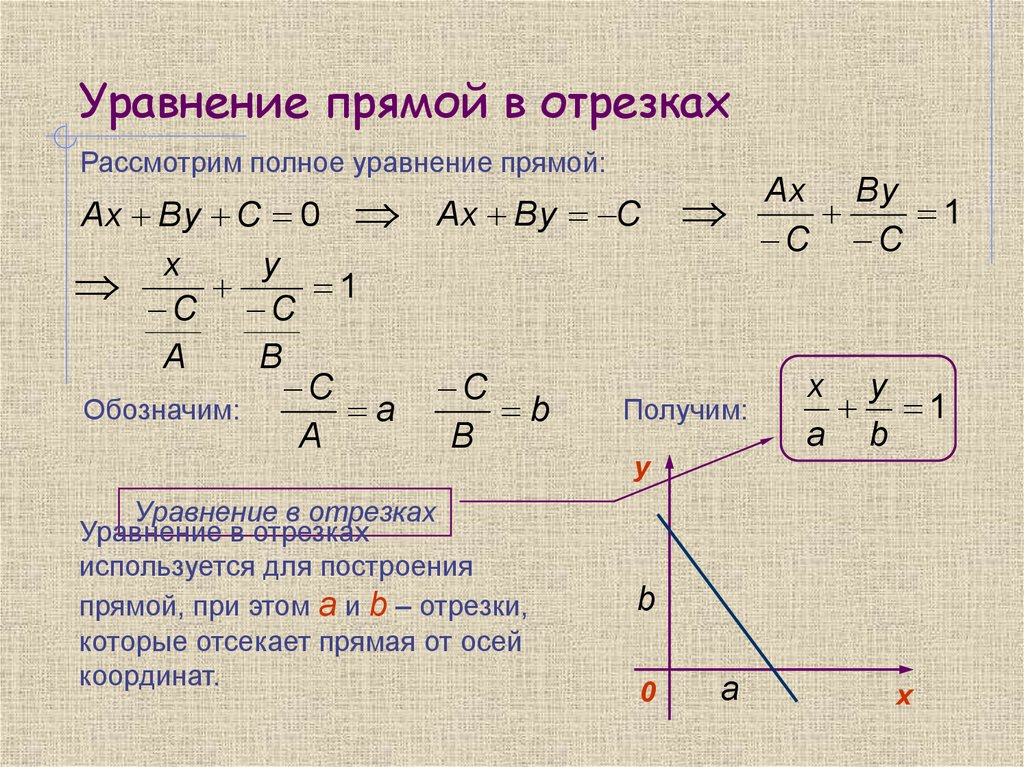
8. Уравнение прямой в отрезках

Рассмотрим полное уравнение прямой:
Ax By C 0
x
y
C C 1
A
B
C
Обозначим:
a
A
Ax By
1
C C
Получим:
x y
1
a b
Ax By C
C
b
B
y
Уравнение в отрезках
Уравнение в отрезках
используется для построения
прямой, при этом a и b – отрезки,
которые отсекает прямая от осей
координат.
b
0
a
х

9.

Параметрическое уравнение прямой
Любой ненулевой вектор, параллельный данной прямой,
называется направляющим вектором этой прямой.
Требуется найти уравнение прямой, проходящей через заданную
точку М0(х0; у0 ) и параллельно заданному вектору q l; m
Очевидно, что точка М (х; у ) лежит на
прямой, только в том случае, если
векторы
q l; m и M 0 M x x0 ; y y0
q
М (х; у )
М0(х0; у0 )
коллинеарны. Тогда по лемме о коллинеарных векторах
имеем M 0 M tq Запишем это равенство в координатах
или
x x0 lt ,
y y0 mt.
Параметрическое
уравнение прямой

10.

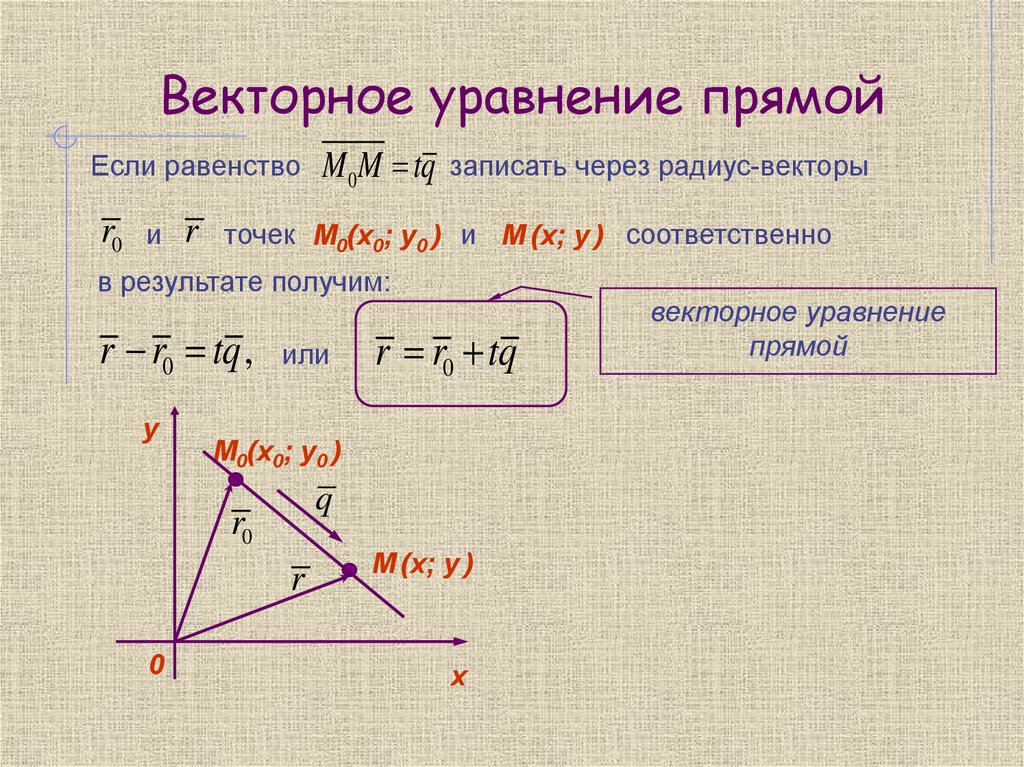
Векторное уравнение прямой
Если равенство
r0 и r
M 0 M tq записать через радиус-векторы
точек М0(х0; у0 ) и М (х; у ) соответственно
в результате получим:
r r0 tq , или
y
М0(х0; у0 )
q
r0
r
0
r r0 tq
М (х; у )
х
векторное уравнение
прямой

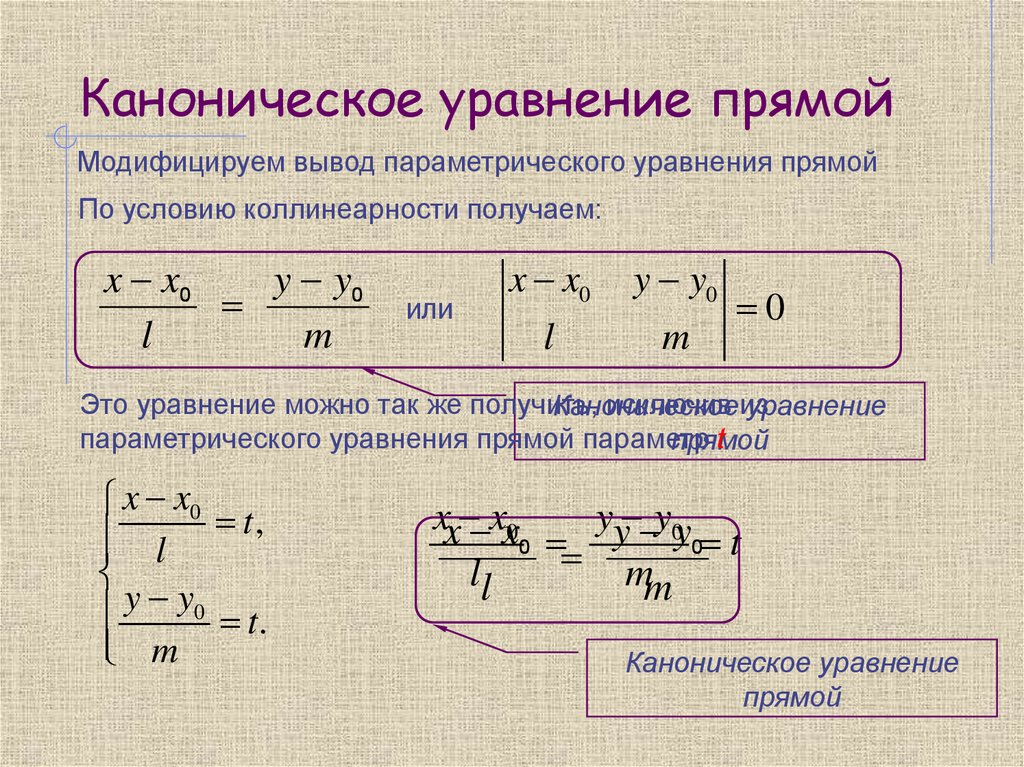
11. Каноническое уравнение прямой

Модифицируем вывод параметрического уравнения прямой
По условию коллинеарности получаем:
x x0
y y0
l
m
или
x x0
l
y y0
0
m
Это уравнение можно так же получить,
исключив из
Каноническое
уравнение
параметрического уравнения прямой параметр
t
прямой
x x0
l t ,
y y0 t.
m
xx xx0
yy y0y
0
0 t
ll
mm
Каноническое уравнение
прямой

12.

Связь координат вектора - нормали
с направляющим вектором прямой
A x x0 B y y 0 0
сравнивая с
x x0
l
имеем
m x x0 l y y0 0
y y0
0
m
q B; A
Координаты
направляющего вектора
через координаты векторанормали

13.

Нормальное уравнение прямой
y
М
n
Определим прямую при помощи
перпендикулярного ей единичного
вектора n
и расстояния р>0 до
прямой от начала системы координат.
Вектор n
однозначно
n cos
, sin определяется
своим углом с осью ОХ, который
отсчитывается
часовой
M ( x, y) L против
хода
прn OM
p
стрелки.
Координаты
его
х
определяются
этот
пр OMчерез
OM
nугол.
0
n
Итак, OM n p
Перейдем к равенству координат
x cos y sin p 0
Нормальное уравнение
прямой

14.

Преобразование общего уравнения прямой в
её нормальное уравнение
Ax By C 0
x cos y sin p 0
Путем деления общего уравнения прямой на нормирующий
множитель A2 B 2 , знак которого выбирается
противоположным знаку С.
Пример
Написать нормальное уравнение прямой, если 3 х 4 у 10 0
Вычислим нормирующий множитель А В 3 ( 4) 5
3
4
х у 2 0
В данном случае имеем
5
5
2
3
4
р 2, cos , sin
5
5
,а arccos
2
3
5
2
2

15. Уравнение прямой, проходящей через две точки

Пусть прямая проходит через две заданные и отличные друг от
друга точки: М1(х1; у1 ) и М2(х2; у2 ).
q
М2(х2; у2 )
М1(х1; у1 )
Тогда в качестве направляющего вектора в каноническом
уравнении можно взять вектор:
q M1M 2 x 2 x1; y 2 y 1
x x1
y y1
y2m
y1
x2 l x1
Уравнение прямой,
проходящей через две
заданные точки

16. Уравнение прямой с угловым коэффициентом

Если прямая не параллельна оси OY и имеет направляющий
вектор q l; m , то угловой коэффициент k этой прямой
равен тангенсу угла наклона прямой к оси OX.
y
mq
0
m
k tg
l
l
x x0
y y0
l
m
х
Уравнение прямой по точке
и угловому коэффициенту
m
y y0 k ( x x0 )
l
y y0 kx kx0 y kx yb0 kx0
Уравнение прямой с
=b
угловым
коэффициентом

17. Пример

Прямая проходит через точку М(1; 2 ) и имеет направляющий
вектор: q { 1; 3 }
Написать: каноническое, общее уравнение прямой, уравнение
прямой в отрезках, уравнение с угловым коэффициентом.
Найти нормальный вектор прямой, отрезки, которые отсекает
прямая от осей координат и угол, который составляет прямая с
осью OX.
1. Каноническое уравнение:
2. Общее уравнение:
3x y 5 0
x 1 y 2
1
3
x 1 y 2
1
3
3 ( x 1) ( y 2 )

18. Пример

3. Уравнение в отрезках: 3 x y 5 0
3x y
1
5 5
x y
1
5
5
3
a
5
3
4. Уравнение с угловым коэффициентом:
b 5
3x y 5 0
y 3 x 5
y
b
М
q
0
a
х
3x y 5
k tg 3

19. Угол между двумя прямыми

Пусть две прямые L1 и L2 заданы общими уравнениями:
L1 :
L2 :
A1x B1y C1 0
A2 x B2 y C2 0
L2
Угол между этими прямыми
определяется как угол между
нормальными векторами к этим прямым:
n1 A1;B1
n2
n1
n2 A2 ;B2
n1 n2
cos cos(n1; n2 )
n1 n2
A1 A2 B1 B2
A12 B12 A22 B22
A1 A2 B1 B2 0
L1 L2
A1 B1
A2 B2
L1 ll L2
L1

20. Угол между двумя прямыми

Пусть две прямые L1 и L2 заданы каноническими уравнениями:
L1 :
L2 :
x x1 y y 1
l1
m1
x x2 y y 2
l2
m2
L2
q2
Угол между этими прямыми определяется
как угол между направляющими векторами
к этим прямым: q1 l1;m1
q2 l 2 ;m2
cos cos(q1; q2 )
l1 l 2 m1 m2 0
l1 m1
l 2 m2
q1
q1 q2
q1 q2
l1 l 2 m1 m2
l12 m12 l 22 m22
L1 L2
L1 ll L2
L1

21. Угол между двумя прямыми

Пусть две прямые L1 и L2 заданы уравнениями с угловыми
коэффициентами:
y
L
L1 :
y k1x b1
L2 :
y k2 x b2
2
2 1
k1 tg 1
1
k2 tg 2
2
0
tg 2 tg 1
k 2 k1
tg tg ( 2 1 )
1 tg 2 tg 1
1 k 2 k1
k1 k2 1
k1 k2
L1 L2
L1 ll L2
х
L1

22. Расстояние от точки до прямой

Пусть необходимо найти расстояние от точки М0(х0; у0 ) до
прямой, заданной общим уравнением: Ax By C 0
М0(х0; у0 )
n
Пусть М1(х1; у1 ) – основание
перпендикуляра, опущенного из
точки М0 на прямую L.
d
М1(х1; у1 )
d M1M0 x0 x1; y 0 y1
L
Найдем скалярное произведение векторов n
A; B и M M
n M1M0 n M1M0 cos
0
или
n M1M0 n M1M0
cos 1
n d
Найдем скалярное произведение в координатной форме:
1
0

23. Расстояние от точки до прямой

n M1M0 A( x0 x1 ) B( y 0 y1 ) Ax0 Ax1 By0 By1
Ax0 By 0 Ax1 By1
Точка М1(х1; у1 ) принадлежит прямой L , следовательно:
Ax1 By1 C 0
n M1M0 Ax0 By 0 C
n M1M0 n d
Ax0 By 0 C
d
n
Ax1 By1 C
n d Ax By C
0
d
Ax0 By 0 C
A2 B 2
0

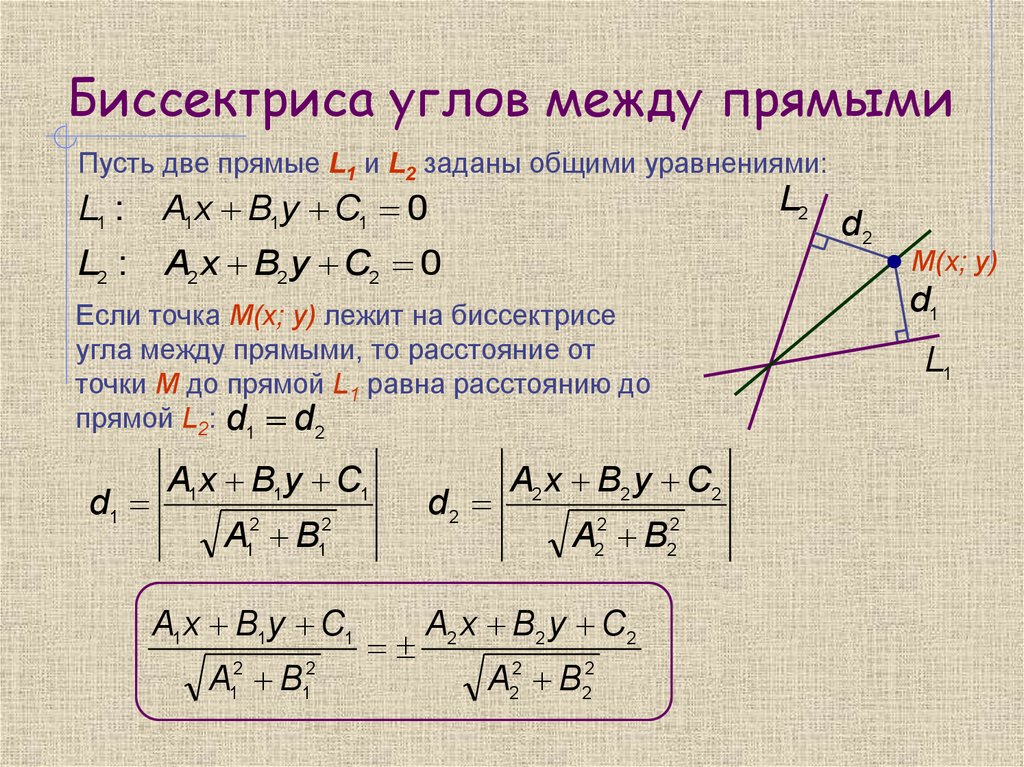
24. Биссектриса углов между прямыми

Пусть две прямые L1 и L2 заданы общими уравнениями:
L1 :
A1x B1y C1 0
L2 :
A2 x B2 y C2 0
L2
M(x; y)
Если точка M(x; y) лежит на биссектрисе
угла между прямыми, то расстояние от
точки М до прямой L1 равна расстоянию до
прямой L2: d1 d2
d1
A1x B1y C1
A B
2
1
2
1
d2
d2
A2 x B2 y C2
A22 B22
A1A
x1
y1y C
xB
1B
1C1 AA2 x2 x BB2 y2 y CC2 2
2 2
2 2
A1A 1 B
AA2222 BB2222
1B1
d1
L1

25. Пример

Даны вершины треугольника: А(1; 1); В(10; 13); С(13; 6)
Найти: Уравнения высоты, медианы и биссектрисы,
проведенных из вершины А.
1. Уравнение высоты:
x 10 y 13
(ВС):
13 10 6 13
x 10 y 13
3
7
А
7x 70 3y 39 7x 3y 109 0
n {7;3}
(АН):
q {7; 3 }
3x 7y 4 0
x 1 y 1
7
3
В
Н
С
3x 3 7y 7

26. Пример

В
2. Уравнение медианы:
т. М:
xM
yM
BM
MC
x B xC
2
yB yC
2
1
А
10 13
11 . 5
2
13 6
9 .5
2
x 1
y 1
11 . 5 1 9 . 5 1
M (1 1 . 5 ; 9 . 5 )
С
x 1 y 1
10 . 5 8 . 5
8,5x 10,5 y 2 0
М
8 .5 x 8 .5 1 0 .5 y 1 0 .5
1 7 x 2 1y 4 0

27. Пример

В
4. Уравнение биссектрисы:
(АВ):
x 1 y 1
10 1 13 1
x 1 y 1
9
12
12x 9y 3 0
12x 12 9y 9
4x 3y 1 0
x 1 y 1
x 1 y 1
(АС):
13 1 6 1
12
5
4x 3y 1
5 x 12 y 7
4 ( 3 )
5 ( 12 )
2
К
С
5x 12y 7 0
5x 5 12y 12
2
А
2
2
4x 3y 1
5 x 12 y 7
5
13
5 2 x 3 9 y 1 3 2 5 x 6 0 y 3 5

28. Пример

Для биссектрисы внутреннего угла треугольника должно
выполняться условие:
k AB k AK k AC
или
4x 3y 1 0
5x 12y 7 0
k AC k AK k AB
4
1
y x
3
4
5
7
y x
12
12
4
3
5
k AC
12
k AB
2 7 x 2 1y 4 8 0
9
16
9
y
x
9x 7y 16 0
k AK
7
9
7
2) 5 2 x 3 9 y 1 3 ( 2 5 x 6 0 y 3 5 ) 7 7 x 9 9 y 2 2 0
1) 5 2 x 3 9 y 1 3 2 5 x 6 0 y 3 5
7x 9y 2 0
7
2
y x
9
9
7
k AK
9
5 7 4
12 9 3