Похожие презентации:
Геометрические приложения определенного интеграла
1. Геометрические приложения определенного интеграла
Схемы применения определенного интегралаВычисление площадей плоских фигур
Полярная система координат
Вычисление длины дуги плоской кривой
Вычисление объема тела вращения
Площадь поверхности вращения
2. Схемы применения определенного интеграла
Пусть требуется найти значение какой либо геометрической илифизической величины А (площадь, фигуры, объем тела, давление
жидкости на вертикальную пластину и т. д.), связанной с отрезком
[a; b] изменения независимой переменной x.
Для нахождения этой величины можно руководствоваться одной из
двух схем:
1 схема ( метод интегральных сумм)
Схема основана на определении определенного интеграла.
Точками xi разбить отрезок на n частей, в связи с этим
интересующая нас величина разобьется на n элементарных
слагаемых:ΔАi.
Представить каждое элементарное слагаемое в виде
произведения некоторой функции, вычисленной в произвольной
точке элементарного отрезка на его длину : Ai f (ci ) xi
При нахождении ΔАi допускаются упрощения (площадь
криволинейной трапеции заменяем площадью прямоугольника).
3. Схемы применения определенного интеграла
nПолучаем приближенное значение
A
f ( c i ) x i
величины в виде интегральной суммы:
i 1
Искомая величина равна пределу интегральной суммы:
n
b
n
( 0 ) i 1
a
A lim f (ci ) xi f ( x )dx
2 схема ( метод дифференциала)
На отрезке [a; b] выбираем значение х и рассматриваем
переменный отрезок [a; x] . На этом отрезке величина А
становится функцией А(х).
Находим дифференциал функции dA = f(x)dx, где f(x) –
определяемая из условия задачи функция переменной x. Здесь
также возможны различные упрощения.
Находим искомую величину, путем
интегрирования dA в пределах от a до b. A
b
b
a
a
dA f ( x )dx
4. Вычисление площадей плоских фигур
По геометрическому смыслу определенногоинтеграла, площадь криволинейной
трапеции, расположенной выше оси ОХ
равна соответствующему определенному
интегралу :
f (x) 0
y
S
0
a
b
a
b
b
S f ( x )dx (1)
a
Если криволинейная трапеция
расположена ниже оси ОХ, то ее площадь
может быть найдена по формуле:
y
0
x
S
b
f (x) 0
x
S f ( x )dx (2)
a
Формулы (1) и (2) можно объединить в
одну для случая, когда функция f(x)
сохраняет знак на [a; b]
b
S f ( x )dx
a
5. Вычисление площадей плоских фигур
Площадь фигуры, ограниченнойкривыми y = f1(x) и y = f2(x), прямыми
x = a, x = b при условии f2 ( x ) f1( x )
находится по формуле:
b
y
f2(x)
S
0
a
S f2 ( x ) f1( x ) dx
a
Если плоская фигура имеет «сложную»
форму, то прямыми, параллельными оси OY,
ее следует разбить на части так, чтобы можно
было применить известные формулы.
Замечание. Иногда удобно
использовать приведенные
формулы по переменной y
(считая x функцией от y)
b
x
f1(x)
y
S3
S1
0 a
S2
S4
bx
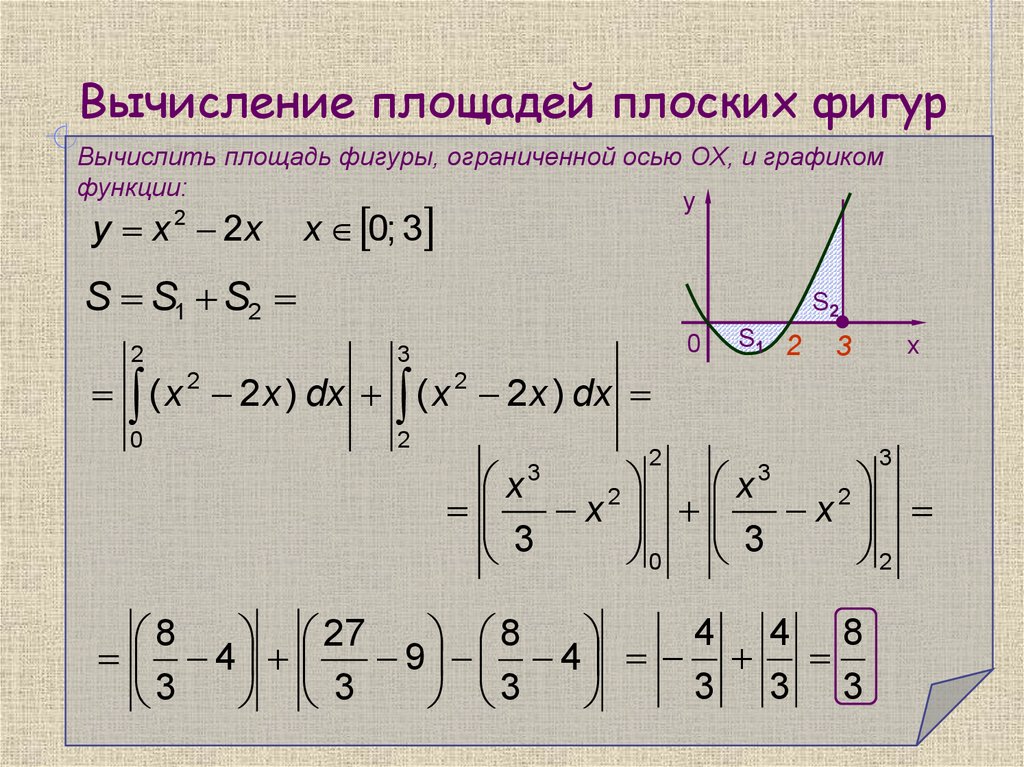
6. Вычисление площадей плоских фигур
Вычислить площадь фигуры, ограниченной осью OX, и графикомфункции:
y
y x 2 2x
x 0; 3
S S1 S2
S2
2
3
0
2
0
S1 2
3
x
( x 2 2 x ) dx ( x 2 2 x ) dx
2
3
x
x
2
2
x
x
3
0 3
2
3
3
4 4 8
8
27
8
4
9 4
3 3 3
3
3
3
7. Вычисление площадей плоских фигур
Найти площадь фигуры, ограниченной линиямиy x2 2 и y x
Найдем точки пересечения данных линий
x 1
x 1
2
2
y x 2
x x 2 0
y 1
x 2 x 2
y x
y x
y x
y 2
A(-1;-1), B(2;2) - точки пересечения данных линий.
2
S
x ( x 2) dx x x 2 dx
2
2
1
2
1
x 2 x3
2
8
1 1
2 x 2 4 2
3
2 3
2 3
1
4,5
8. Вычисление площадей плоских фигур
Если криволинейная трапеция ограничена кривой, заданнойпараметрически, прямыми x = a, x = b и осью OX:
x x(t ),
t ; ,
y y(t );
S y (t ) x (t ) dt
Найти площадь фигуры, ограниченной первой аркой циклоиды
x a(t sin t ),
y a 1 cos t и отрезком оси абсцисс
Найдем пределы изменения
параметра t
0 a t sin t ; sin t t t1 0
2 a a t sin t ; t sin t 2 t2 2
9. Вычисление площадей плоских фигур
22
0
0
S a 1 cost a t sin t dt a 2
a2
2
2
0
2
0
1 cost 1 cost dt
2
2
2
1 cost dt a 1 2 cost cos t dt
1
1 cos 2t
2
2 3
a 1 2 cost
dt a t 2 sin t sin 2t
4
2
0
2
0
2
3 a 2
10. Полярная система координат
Полярная система координат задается точкой О, называемойполюсом и полярной осью р.
М
Положение точки М на плоскости
r
определяется двумя числами: ее
расстоянием r от полюса О,
φ
и углом φ, образованным отрезком ОМ
с полярной осью, отсчитываемый
против часовой стрелки.
0
Числа r и φ называют полярными координатами точки М ,
записывают: М(r ; φ).
; - полярный угол
r 0;
- полярный радиус
р
11. Полярная система координат
Установим связь между прямоугольнымии полярными координатами.
Для этого совместим полюс О с
началом координат системы координат
XOY, а полярную ось с положительным
направлением оси OX.
Y
М
y
r
φ
0
X
х
р
Прямоугольные координаты точки M выражаются через полярные
координаты следующим образом:
x r cos ,
y r sin .
Полярные координаты выражаются через декартовы по формулам:
r x 2 y 2 ,
y
tg x .
Определяя величину φ следует установить
четверть , в которой лежит угол и учитывать,
что .
12. Полярная система координат
Найдем площадь S криволинейного сектора, то есть плоскойфигуры, ограниченной непрерывной линией r = r(φ) и двумя
лучами: φ = α и φ = β (α< β).
Для решения задачи используем схему 2 – метод дифференциалов.
B
Будем считать часть искомой
площади S, как функцию угла φ, то
есть S = S(φ), где α < φ < β
A
dφ
β
α
0
φ
р
Если текущий полярный угол φ
получит приращение Δφ = dφ, то
приращение площади ΔS равно
площади криволинейного сектора
OAB.
13. Полярная система координат
Дифференциал dS, представляетсобой главную часть приращения
ΔS и равен площади кругового
сектора OAC радиуса r(φ) с
центральным углом dφ.
C
B
A
dS
dφ
β
α
φ
р
0
1 2
dS r d
2
Интегрируя полученное равенство в пределах от α до β, получим
искомую площадь:
1 2
S r ( ) d
2
14. Полярная система координат
Вычислить площадь фигуры, ограниченной кардиоидой r 1 cosКардиоида симметрична относительно
полярной оси, поэтому найдем площадь
половины кардиоиды.
0
р
2
1
1
2
S 1 cos d
2
20
S 1 2 cos cos2 d
0
3
1 1
1 2 cos cos 2 d d 2 cos d
20
2 2
0
0
1
3
1
3
cos 2 d 2 sin 0 sin 2 0
20
2 0
4
2
15. Полярная система координат
Найти площадь фигуры, заключенной внутри лемнискаты Бернуллиr 2 a 2 cos2
В силу симметрии достаточно вычислить
одну четверть искомой площади и
умножить ее на четыре.
1
S 4
2
/4
0
/4
1
a cos 2 d 2a sin 2
0
2
2
2
a sin sin 0 a
2
2
2
16. Вычисление длины дуги плоской кривой
Пусть в прямоугольной системе координат задана плоская криваяy = f(x), где a x b .
N
y
B
M
Найдем формулу длины дуги L,
Δy
используя метод дифференциалов.
Δx
Возьмем на отрезке [a; b]
произвольное значение x и рассмотрим
переменный отрезок [a; x] . На нем
величина L становится функцией от x.
A
0
аx
x+Δx b
Найдем дифференциал dL функции L = L(x) при изменении x
на маленькую величину Δx = dx: dL L ( x )dx
Найдем L (x ) заменяя бесконечно малую дугу MN хордой L
2
2
2
L
x y
y
L ( x ) lim
lim
lim 1
x 0 x
x 0
x 0
x
x
1 y 2 dL 1 y 2 dx
x
17. Вычисление длины дуги плоской кривой
Интегрируя dL в пределах от а до bполучим:
b
L 1 y 2 dx
a
Если уравнение кривой AB задано в параметрической форме:
x x(t ),
t ;
y y(t );
x( ) a,
то длина дуги кривой находится по
формуле:
x( ) b,
L x 2 y 2 dt
Если кривая AB задана в полярных координатах:
r r ( ), ,
то длина дуги кривой находится по
формуле:
L r 2 r 2 d
18. Вычисление длины дуги плоской кривой
Вычислить длину дуги окружности, заданной уравнением: x 2 cost ;от точки А(2; 0) до точки B(1;
y 2 sin t
3)
Найдем как изменяется параметр t при
переходе от точки А к точке В:
y
В
А
2
0
2 2 cost;
t 0
0 2 sin t
x
1 2 cost;
t
3
3 2 sin t
3
3
2
2
L (2 cos t ) 2 (2 sin t ) 2 dt 4 sin t 4 cos t dt
0
3
2dt 2t
0
3
0
2
3
0
19. Вычисление длины дуги плоской кривой
Вычислить длину астроидыx a cos3 t ,
y a sin 3 t
Кривая симметрична относительно
обеих координатных осей, поэтому
найдем длину ее четвертой части и
результат умножим на четыре.
2
L 4
(a cos t ) (a sin t ) dt
2
3
3
2
0
2
4
a 3cos t sin t a 3sin t cost dt 12a cos t sin t sin t cos t dt
2
2
2
2
2
2
4
0
0
12a
4
2
2
0
cos2 t sin 2 t cos2 t sin 2 t dt 12a cost sin tdt 12 a
0
sin t / 2
2 0
6a
2
20. Вычисление объема тела вращения
Пусть вокруг оси OX вращается криволинейная трапеция,ограниченная непрерывной линией y = f(x) > 0, отрезком [a; b] и
прямыми x = a, x = b.
. при вращении фигура
Полученная
y
называется телом вращения.
Объем полученного тела
вычисляется по формуле:
b
0
а
b
x
Vx y 2dx
a
Если криволинейная трапеция, ограниченная
графиком функции x = q(y) > 0, прямыми y = c,
y = d и осью OY, то объем тела, образованного
вращением этой фигуры вокруг оси OY равен:
d
Vy x 2dy
c
21. Вычисление объема тела вращения
Вычислить объем тела, образованного вращениемфигуры, ограниченной линиями:
y x 2;
x 0;
y 4
вокруг оси OY.
y
4
4
0
0
2
0
4
Vy y dy ydy
2
x
4
y
8
2 0
22. Площадь поверхности вращения
Площадь поверхности, образованной вращением вокруг оси ОХдуги кривой y=f(x) между точками с абсциссами а и b выражается
b
формулой
2
S 2 f x 1 f x dx
a
Если кривая задана параметрическими уравнениями
x x(t ),
t ,
y y(t );
то
S 2 y x 2 y 2 dt
Если кривая задана в полярных координатах
r r ( ), ,
то
S 2 r sin r 2 r 2 d
23. Площадь поверхности вращения
Вычислить площадь S поверхности, полученной вращением одной аркициклоиды
x a t sin t ,
y a 1 cos t , 0 t 2
вокруг оси ОХ.
2
S 2 a 1 cost a t sin t a 1 cost dt
2
2
0
2
2 a 2
2
2
1 cost 1 cost sin t dt
0
2
2 a 2
1 cost 1 2 cost cos2 t sin 2 t dt
0
2
2 2 a
2
1 cost
3/ 2
0
2
2
2 t
2
2
a
2
sin
dt
2
0
3/ 2
dt
24. Площадь поверхности вращения
28 a
2
0
2
t t
t
2
2 t
16
a
sin
sin
d
sin dt
2
2 2
2
0
3
3 t
cos
2
t
t
2
2 t
2
2
16 a 1 cos d cos 16 a cos
2
2
2
3 0
0
2
1
1
16 a 2 cos cos3 cos0 cos3 0
3
3
2
64
a
1
1
4
16 a 2 1 1 16 a 2
3
3 3
3























 Математика
Математика








