Lecture 5. Application of derivatives

1.

CALCULUS 1
Lecture 5
Application of derivatives
Aigul Myrzagaliyeva
aigul.myrzagalieva@astanait.edu.kz
Astana IT University

2.

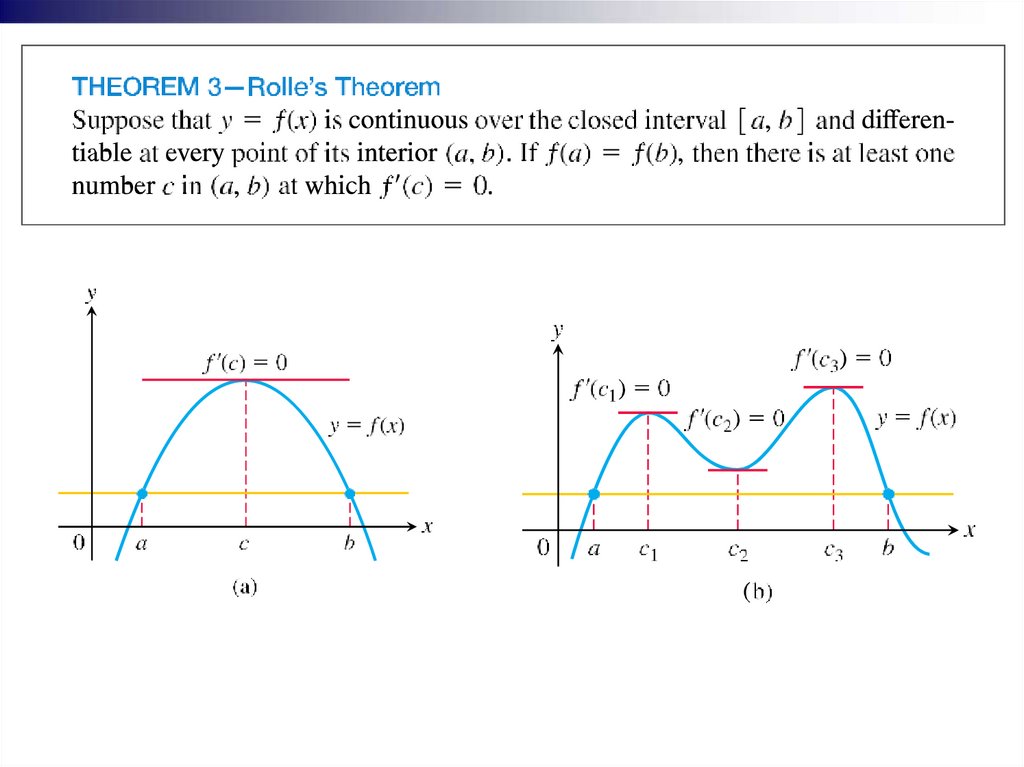
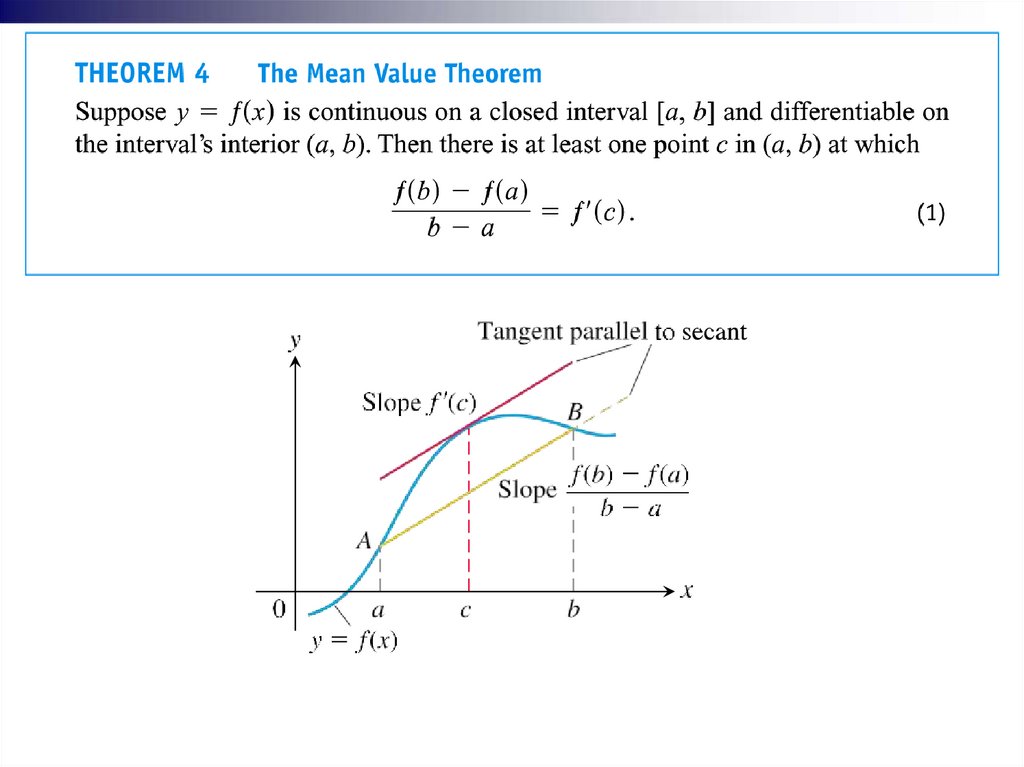
Lecture overview
Extreme Values of Functions
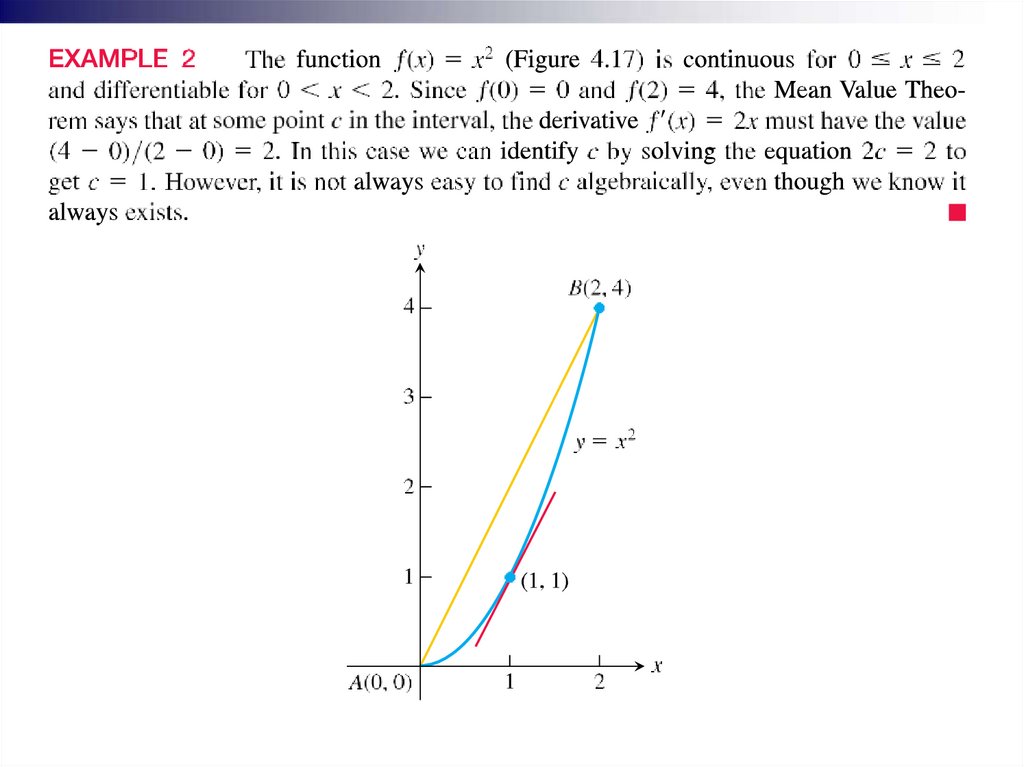
The Mean Value Theorem
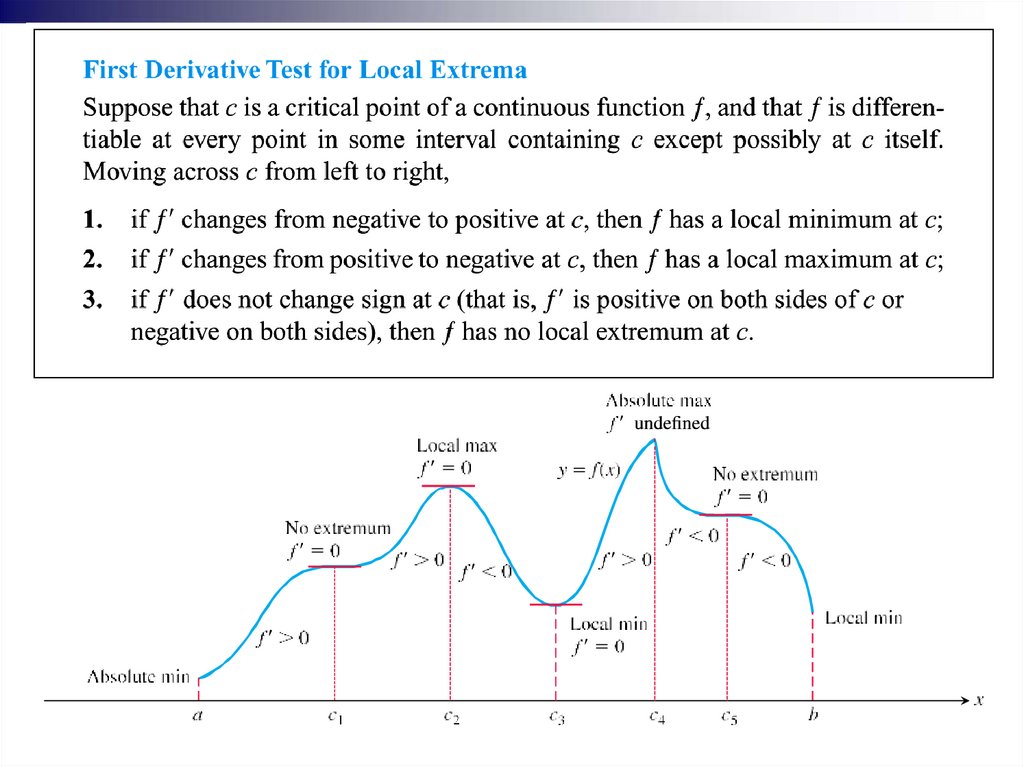
The First Derivative Test
Concavity
Asymptotes
Curve Sketching
Indeterminate Forms and L’Hôpital’s Rule
Applied Optimization Problems

3.

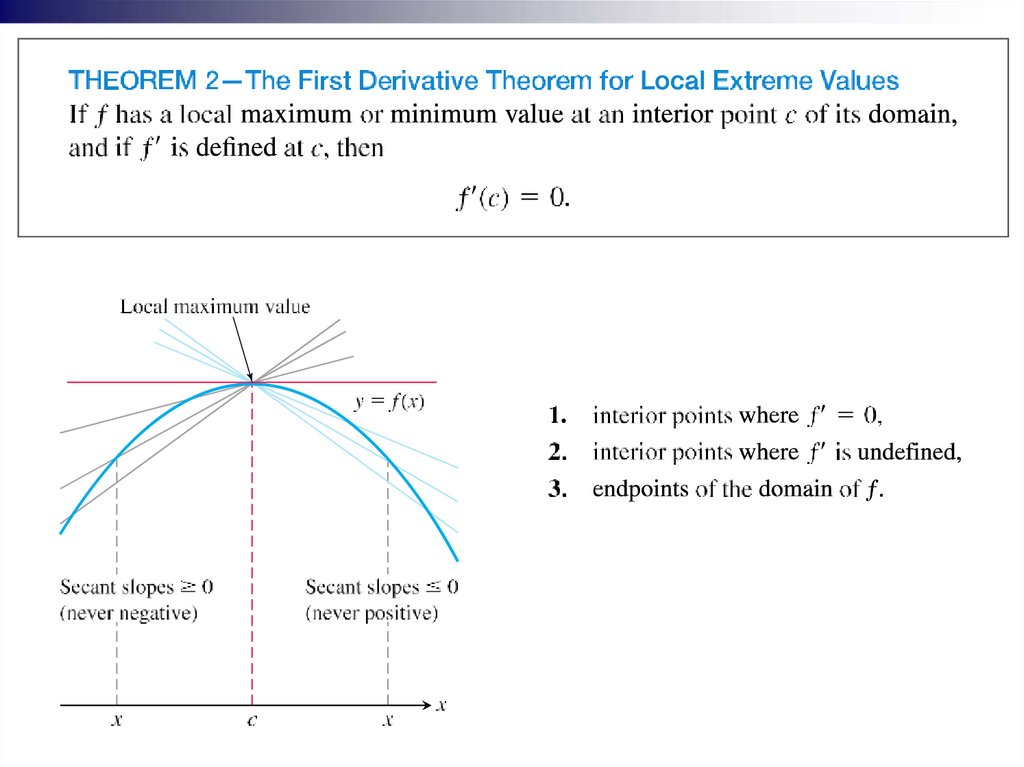
The important application of
derivatives is to find extreme
values
of
functions,
to
determine
and analyze the
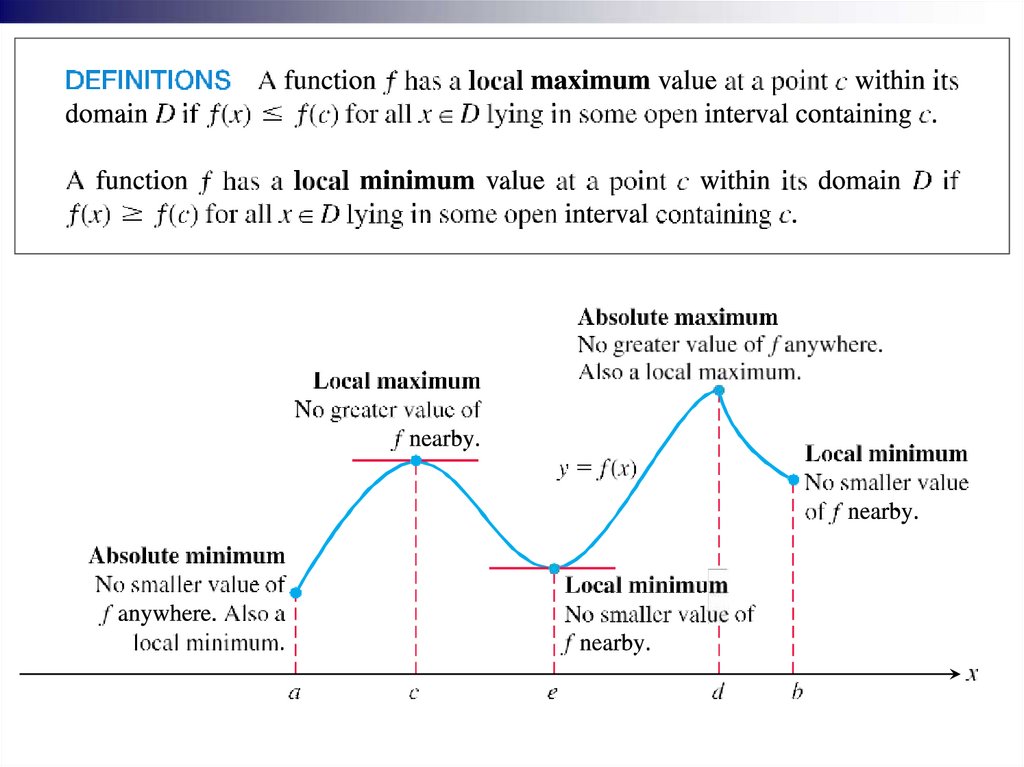
shapes of graphs. Maximum
and minimum values are called
extreme values of the function ƒ.
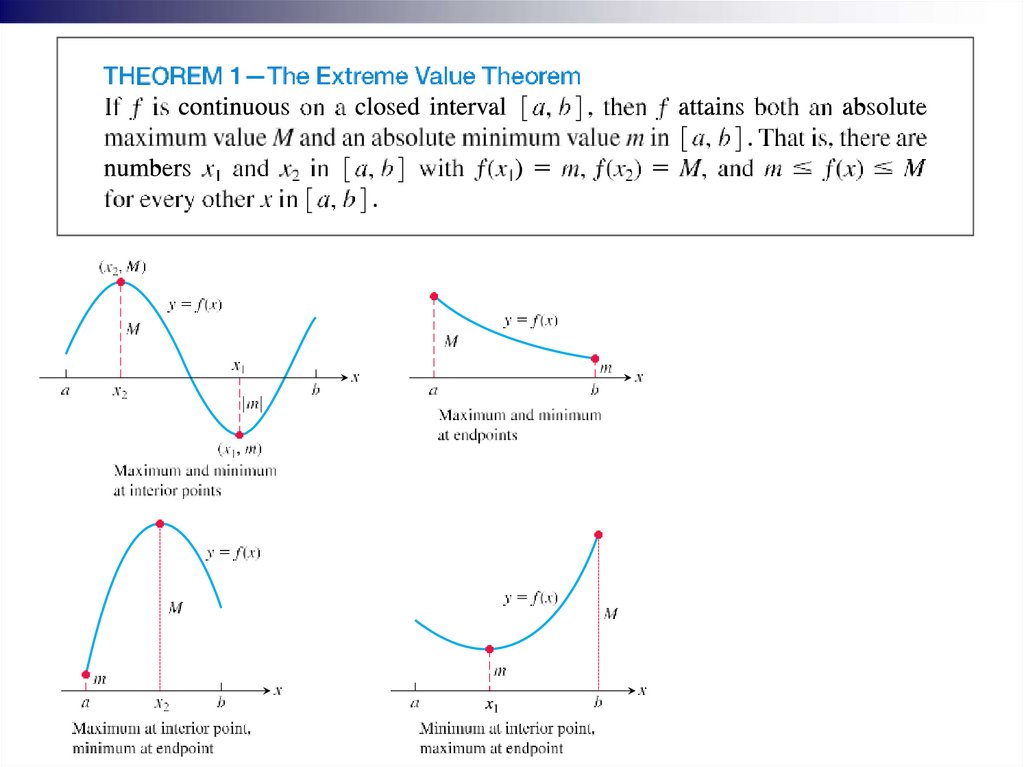
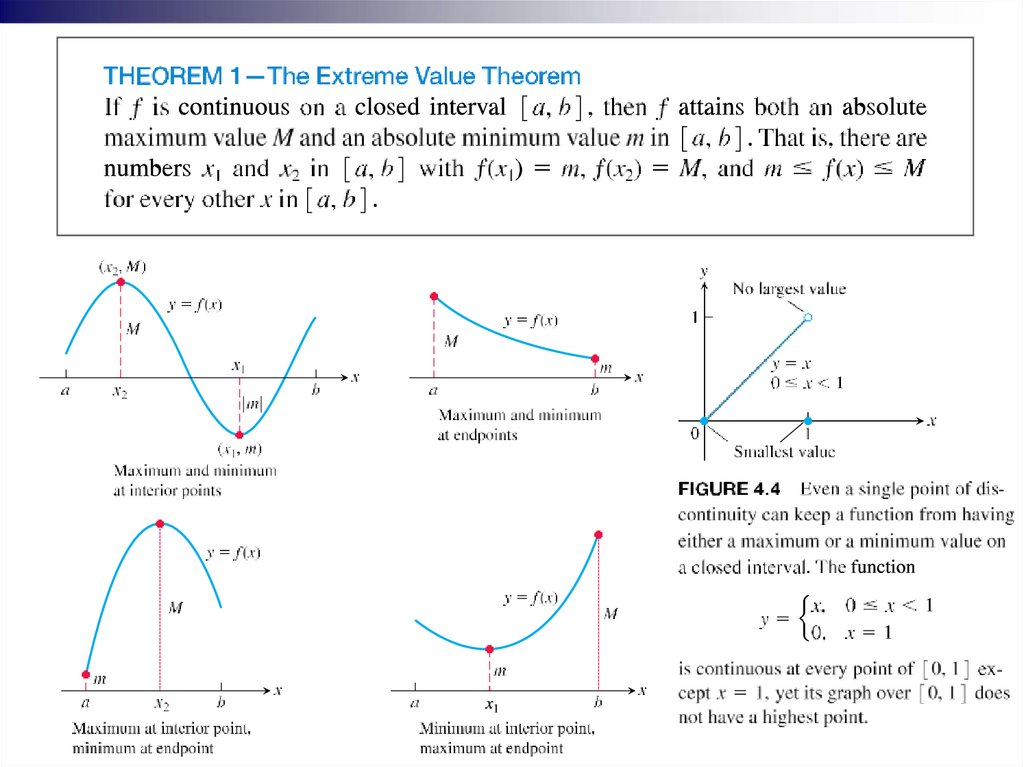
Absolute maxima or minima are
also referred to as global maxima
or minima.

4.

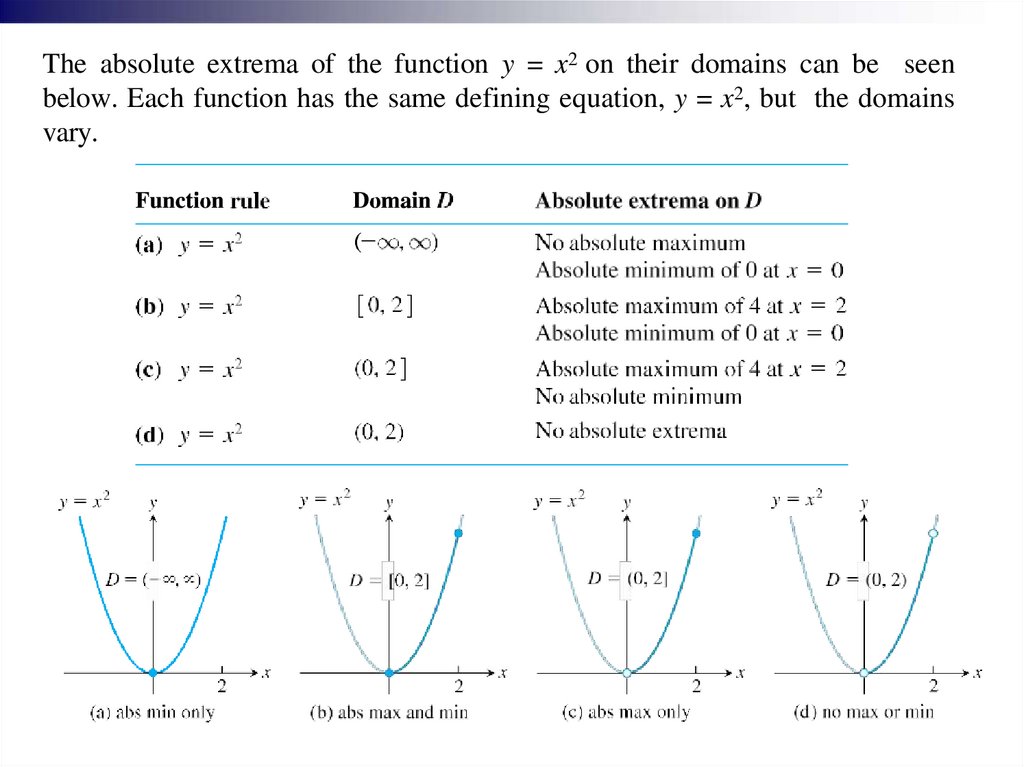
The absolute extrema of the function y = x2 on their domains can be seen
below. Each function has the same defining equation, y = x2, but the domains
vary.

5.

6.

7.

8.

9.

10.

11.

12.

13.

14.

15.

Proofs of the Laws of Logarithms
Proof that ln bx = ln b + ln x

16.

In sketching the graph of a differentiable function, it is useful to know where it
increases (rises from left to right) and where it decreases (falls from left to right)
over an interval.

17.

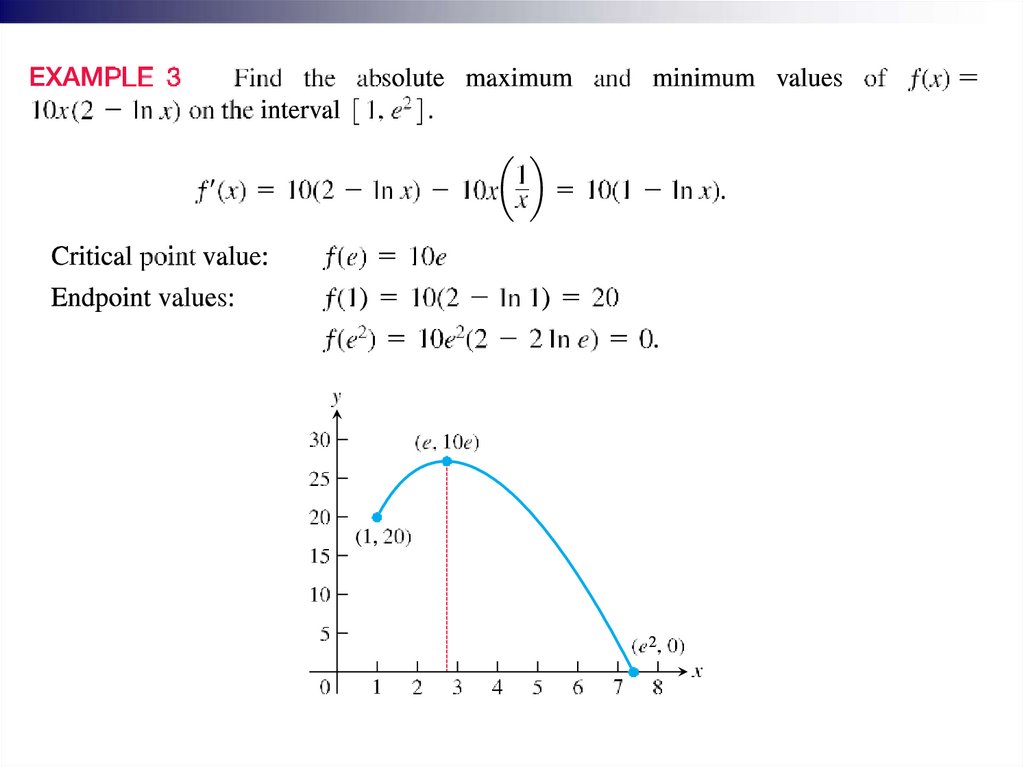
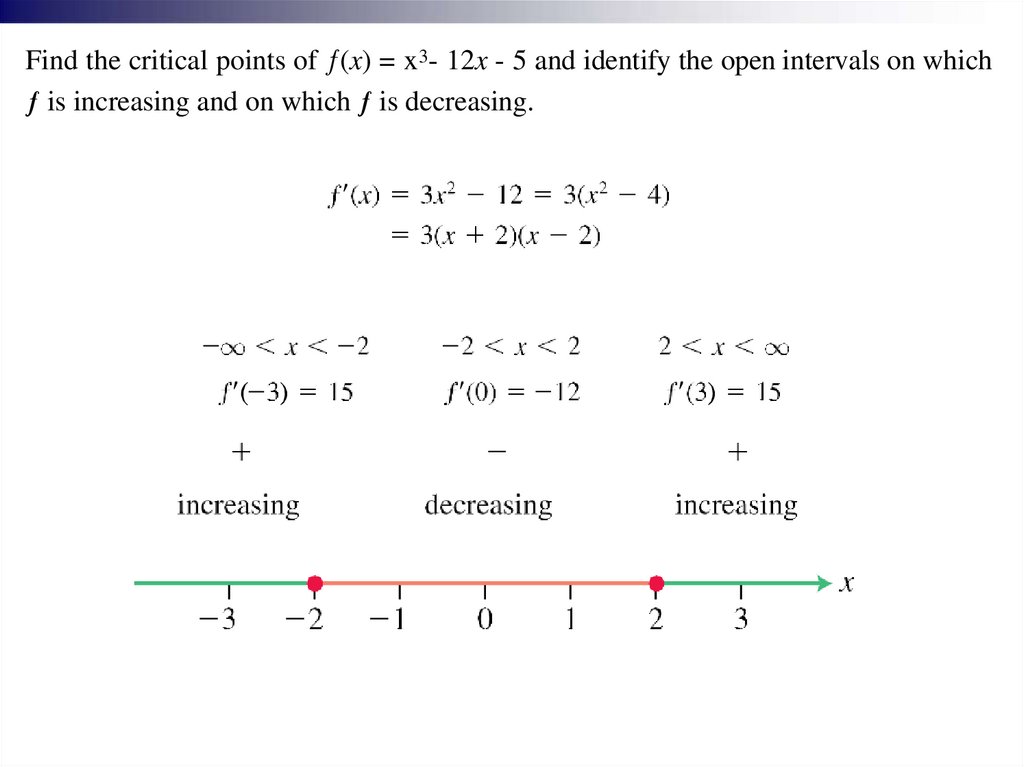
Find the critical points of ƒ(x) = x3- 12x - 5 and identify the open intervals on which
ƒ is increasing and on which ƒ is decreasing.

18.

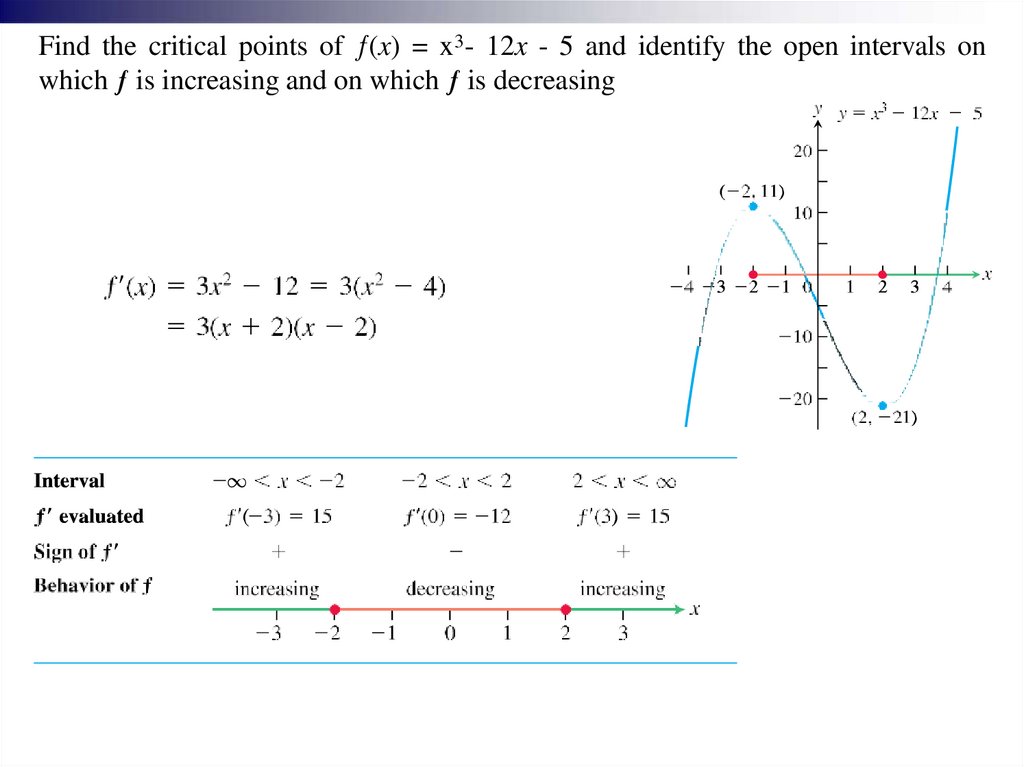
Find the critical points of ƒ(x) = x3- 12x - 5 and identify the open intervals on
which ƒ is increasing and on which ƒ is decreasing

19.

20.

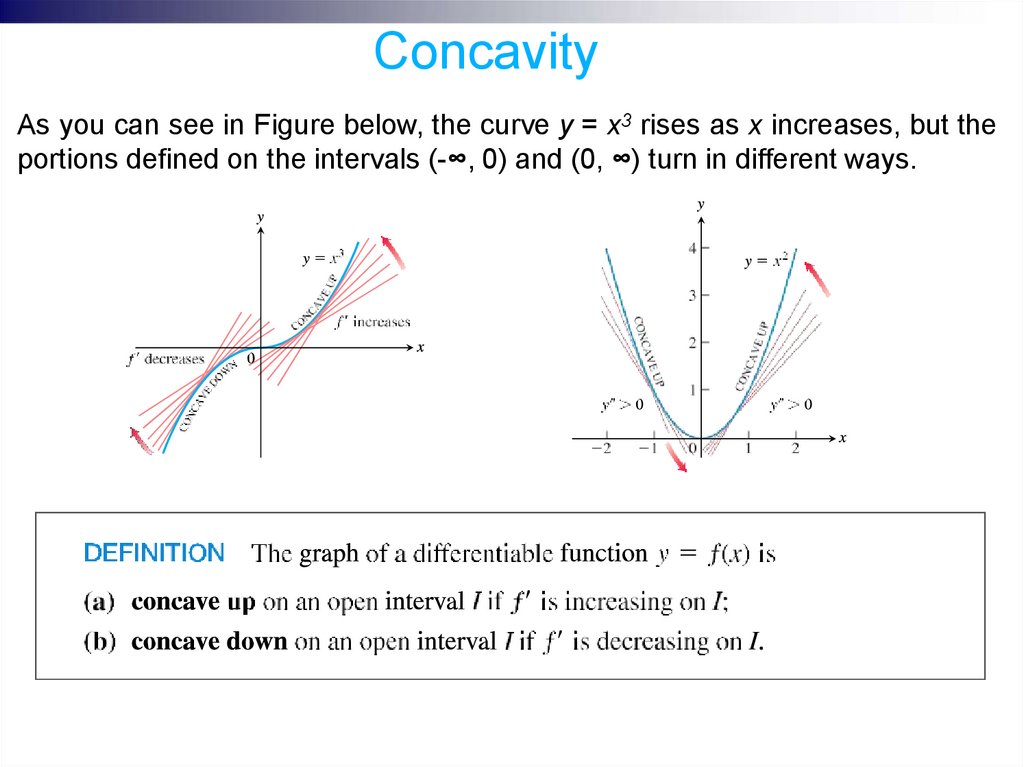
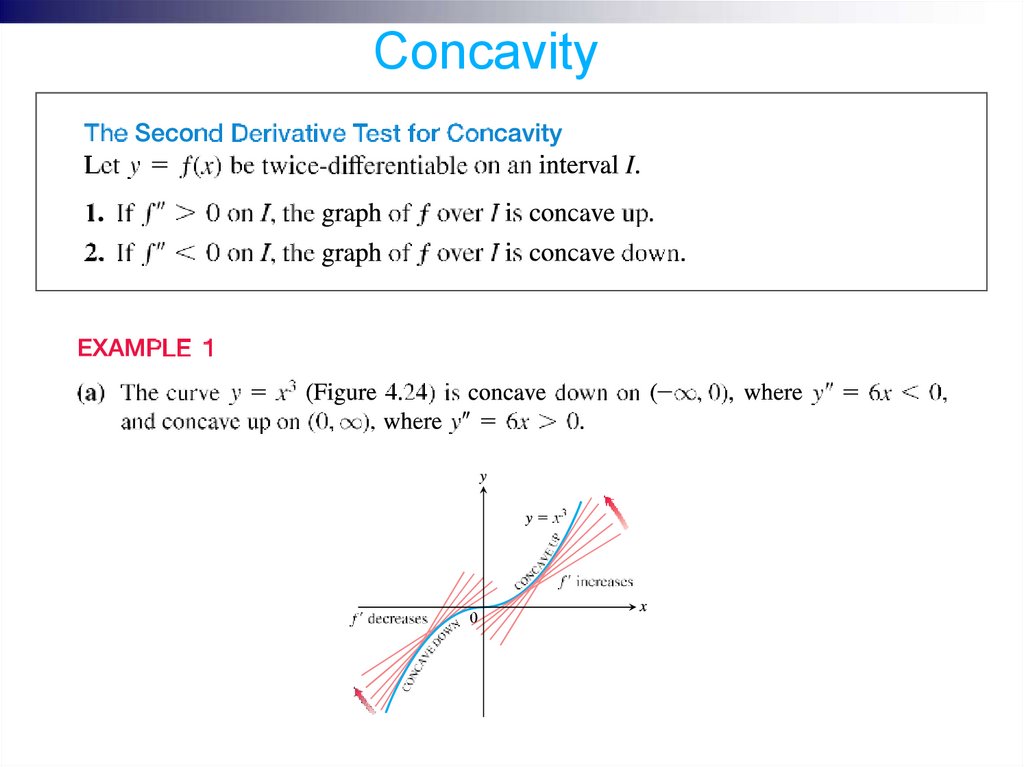
Concavity
As you can see in Figure below, the curve y = x3 rises as x increases, but the
portions defined on the intervals (-∞, 0) and (0, ∞) turn in different ways.

21.

Concavity

22.

23.

24.

25.

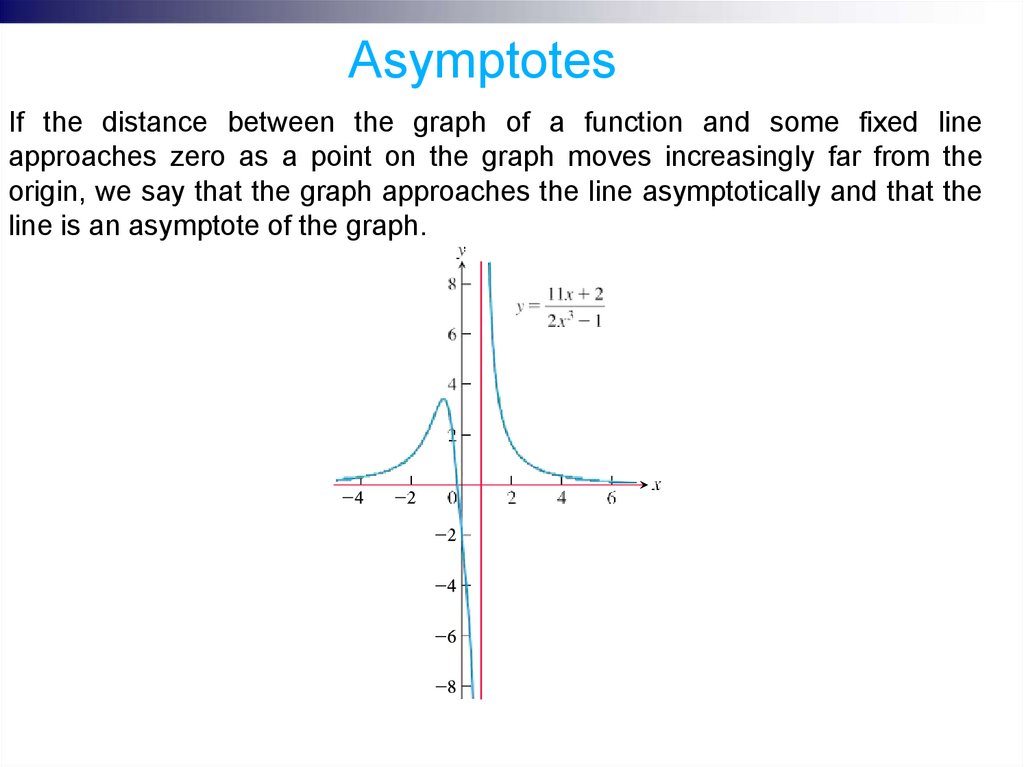
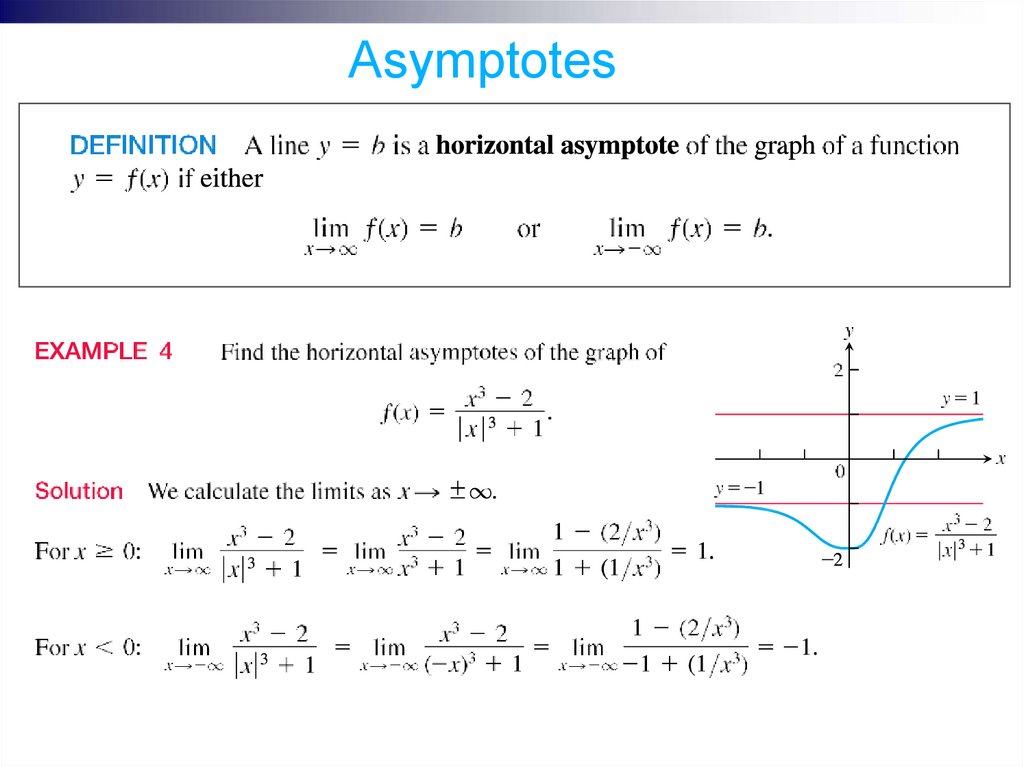
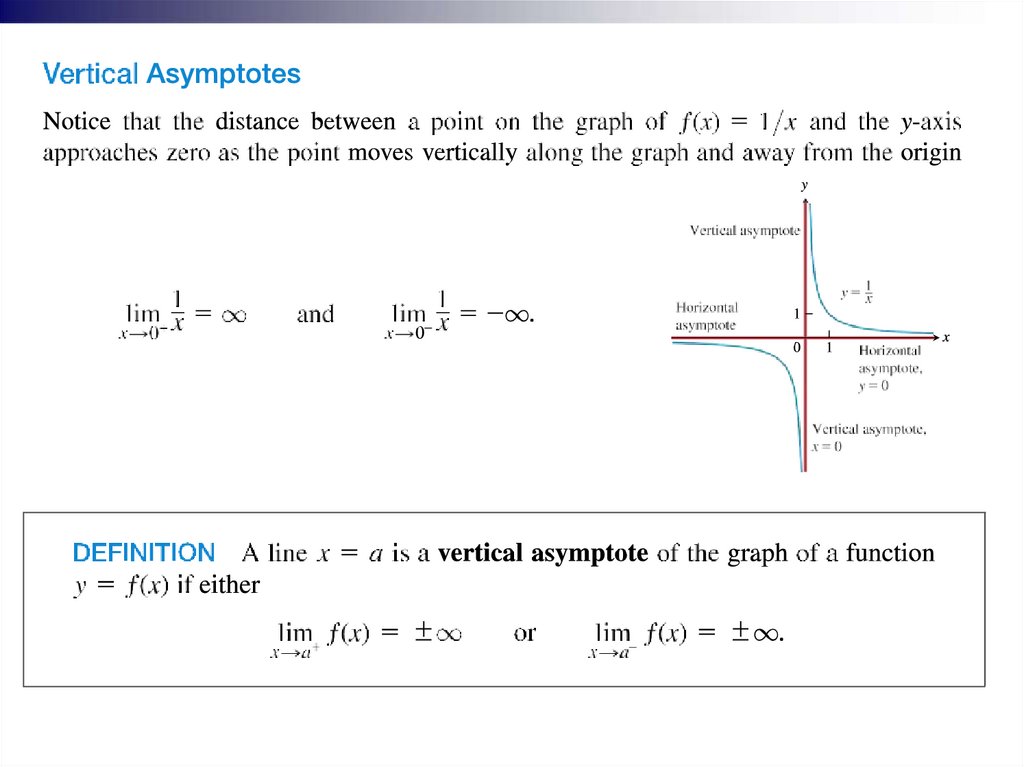
Asymptotes
If the distance between the graph of a function and some fixed line
approaches zero as a point on the graph moves increasingly far from the
origin, we say that the graph approaches the line asymptotically and that the
line is an asymptote of the graph.

26.

Asymptotes

27.

Asymptotes

28.

29.

30.

31.

Sketch a graph of the function

32.

33.

34.

35.

Indeterminate Forms and L’Hôpital’s Rule
Expressions such as “0/0” and “∞/ ∞” look something like ordinary numbers. We
say that they have the form of a number. But values cannot be assigned to them in
a way that is consistent with the usual rules to add and multiply numbers. We are
led to call them “indeterminate forms.”

36.

37.

Indeterminate Powers
Limits that lead to the indeterminate forms 1∞, 00, and ∞0 can sometimes be handled
by first taking the logarithm of the function.

38.

39.

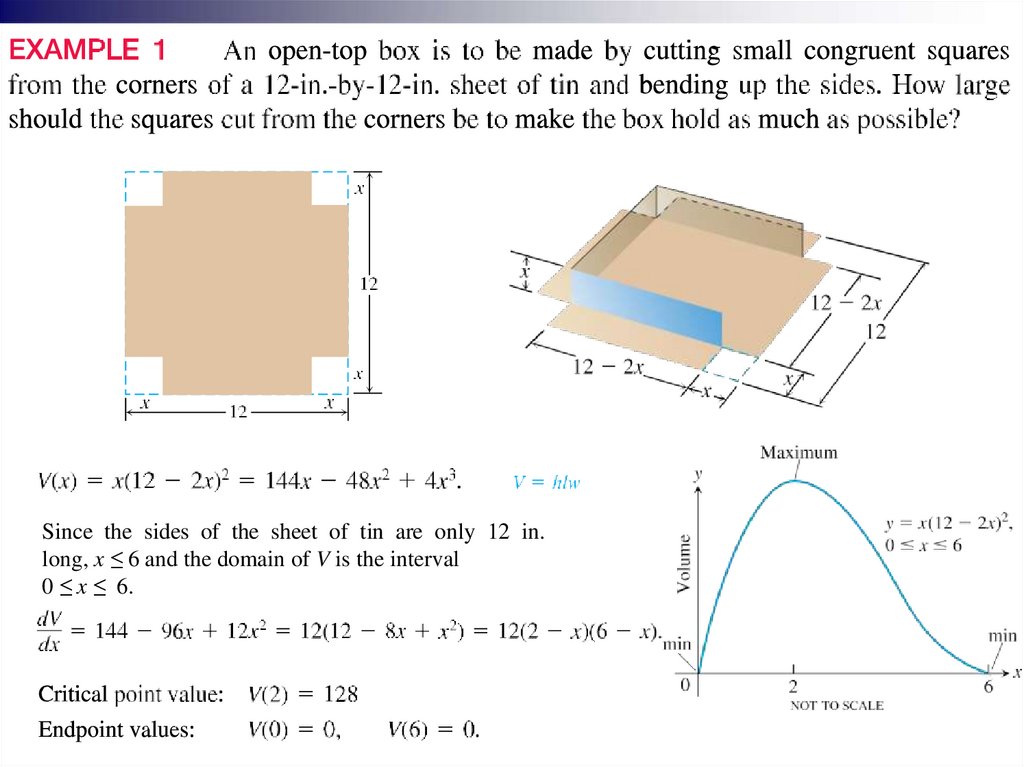
Applied Optimization Problems
What are the dimensions of a rectangle with fixed perimeter having maximum
area? What are the dimensions for the least expensive cylindrical can of a given
volume? Each of these questions asks for the best, or optimal, value of a given
function. We use derivatives to solve a variety of optimization problems.

40.

41.

Since the sides of the sheet of tin are only 12 in.
long, x ≤ 6 and the domain of V is the interval
0 ≤ x ≤ 6.

42.

Since the sides of the sheet of tin are only 12 in.
long, x ≤ 6 and the domain of V is the interval
0 ≤ x ≤ 6.