Matematika fani bo‘yicha ko‘nikmalarni rivojlantirish

1.

Matematika fani bo‘yicha
master-trenerlar uchun
malaka oshirish treningi
Modul 5: Matematika fani bo‘yicha ko‘nikmalarni
rivojlantirish

2.

Bugungi darsning maqsadlari:
Algebraik tugmalar yordamida musbat va manfiy
sonlarni ifodalash va ular ustida amallar bajarish.
Butun sonlar ustida amallarni yechishda nolli
juftliklar va sonning manfiysi tushunchalarini
qo‘llash.
Matematikaga oid ko‘rgazmali qurollardan
foydalanib algebraik ifodalarni tushunishni
ko‘rsatish.
Algebraik tugmalar va muvozanat yondashuvidan
foydalanib, chiziqli tenglamalarni yechish.
Source: Used with permission – Microsoft Stock Image

3.

Algebraik va sonli tugmalar

4.

Keyingi navbatda nimani ko‘rib chiqamiz?
Bilim va ko‘nikmalar
Sonlar va Algebra
Geometriya va
o‘lchashlar
Statistika va ehtimollik
O‘rganish tajribalari
(Matematik jarayonlar, metaanglash va munosabatlar)

5.

Sonlar va Algebra
Sinf: 7 (O‘rta Maktab)
Mavzu: Sonlar va ularning xossalari
Mazmun: manfiy sonlar, butun sonlar, ratsional sonlar, haqiqiy sonlar va ular
ustida to‘rt amal.
O‘rganish tajribasi
O‘quvchilarga quyidagi imkoniyatlar berilishi kerak:
• Algebraik tugmalar yoki boshqa moddiy o’quv qurollari yordamida manfiy
butun sonlarni qo‘shish, ayirish va ko‘paytirishni o`rganish va butun sonlar
ustida to‘rt amalni bajarish bo’yicha ko’nikmalarni hosil qilish.

6.

Oldingi bilimlar
Quyidagilarni tushinish:
• Manfiy sonlar
• Butun sonlar
• Ratsional sonlar
• Haqiqiy sonlar
• Qo‘shish – “birlashtirish, jamlash” degani.
• Ayirish – “olib tashlash” degani.
Source: Used with permission – Microsoft Stoc

7.

Algebraiki va sonli tugmalar
• Biz sonli tugmalar sonini oshiramiz, chunki manfiy sonlarni
qo`shishimiz kerak .
• Masalan, 5 va -5 sonlari mos ravishda quyidagicha ifodalanadi:
1
1
–1
–1
–1
1
1
5
–1
–1
–5

8.

Algebraik va sonli tugmalar
• Tugma
1
sonli tugma deb ataladi.
• Har bir sonli tugmaning quyida ko‘rsatilganidek ikkita tomoni bor :
1
–1
old
orqa
• Biz tugmani aylantirib, uning old yoki orqa tomonini ko‘rsatishimiz mumkin.

9.

Asosiy tushunchalar
Source: Used with permission – Microsoft Stoc

10.

Asosiy tushunchalar
1. Sonning manfiysi
2. Nolli juftlik

11.

1. Songa qarama-qarshi son
• 1 ning manfiysi, ya’ni unga qarama-qarshi son -1 dir. Buni -(1) = -1 deb yozamiz.
• -1 ning manfiysi, ya’ni unga qarama-qarshi son 1 dir. Buni -(-1) = 1 deb yozamiz.
• Sonning qarama-qarshisini uning ishorasini o‘zgartirish orqali olamiz.
Shunday qilib, 4 ning manfiysi (qarama-qarshisi) -4 dir. Masalan: –(4) = –4
Aksincha, -4 ning manfiysi (qarama-qarshisi) 4 dir.
Masalan: – (–4) = 4
• Sonning qarama-qarshisini olish uchun biz uni ifodalovchi tugmani aylantirib,
uning ishorasini o‘zgartiramiz.
• Misol uchun:
- –1 –1 –1
1
1
1
–(–3) = 3

12.

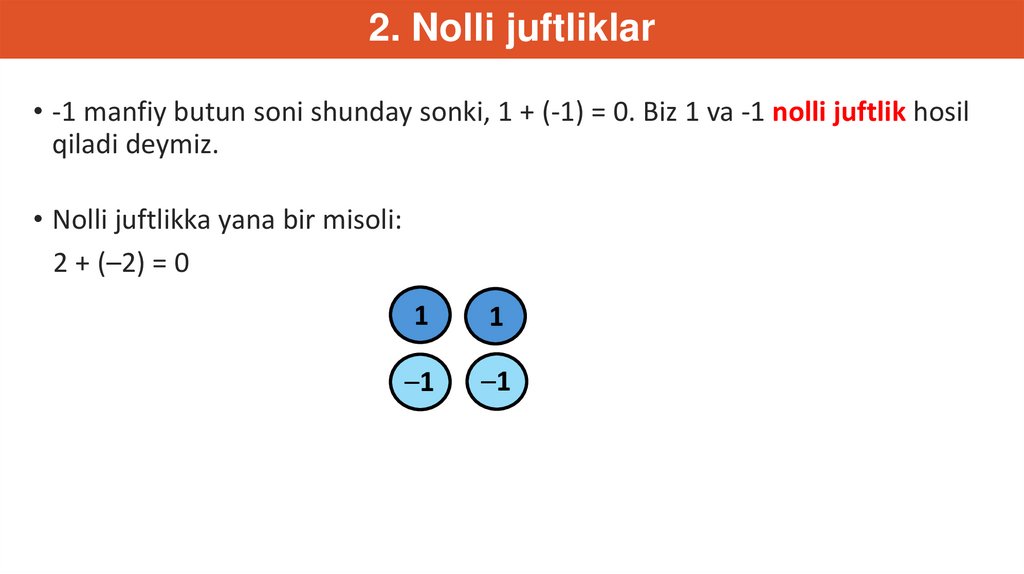
2. Nolli juftliklar
• -1 manfiy butun soni shunday sonki, 1 + (-1) = 0. Biz 1 va -1 nolli juftlik hosil
qiladi deymiz.
• Nolli juftlikka yana bir misoli:
2 + (–2) = 0
1
1
–1
–1

13.

Butun sonlarni qo‘shish va ayirish
Source: Used with permission – Microsoft Stoc

14.

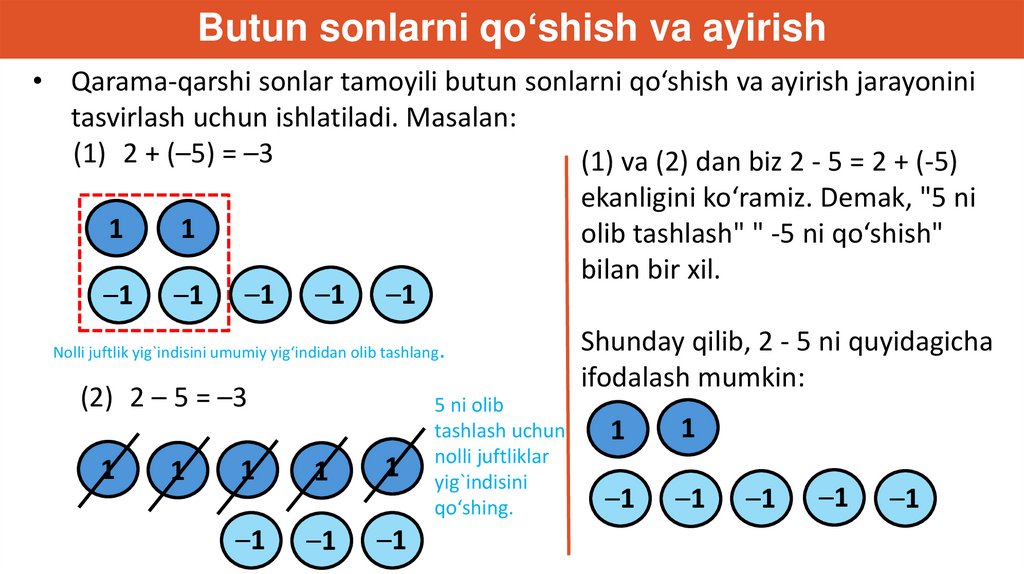
Butun sonlarni qo‘shish va ayirish
• Qarama-qarshi sonlar tamoyili butun sonlarni qo‘shish va ayirish jarayonini
tasvirlash uchun ishlatiladi. Masalan:
(1) 2 + (–5) = –3
(1) va (2) dan biz 2 - 5 = 2 + (-5)
ekanligini ko‘ramiz. Demak, "5 ni
1
1
olib tashlash" " -5 ni qo‘shish"
bilan bir xil.
–1 –1 –1 –1 –1
Nolli juftlik yig`indisini umumiy yig‘indidan olib tashlang.
(2) 2 – 5 = –3
1
1
1
1
1
© All rights reserved
–1
–1
–1
5 ni olib
tashlash uchun
nolli juftliklar
yig`indisini
qo‘shing.
Shunday qilib, 2 - 5 ni quyidagicha
ifodalash mumkin:
1
1
–1
–1
–1
–1
–1

15.

Keling, qo‘llab ko‘ramiz!
3 - 5 ayirmani hisoblang?
Javob berish uchun algebraik va
sonli tugmalardan foydalaning.

16.

Bir xil ishorali ikkita butun sonni
qo‘shish
Source: Used with permission – Microsoft Stoc

17.

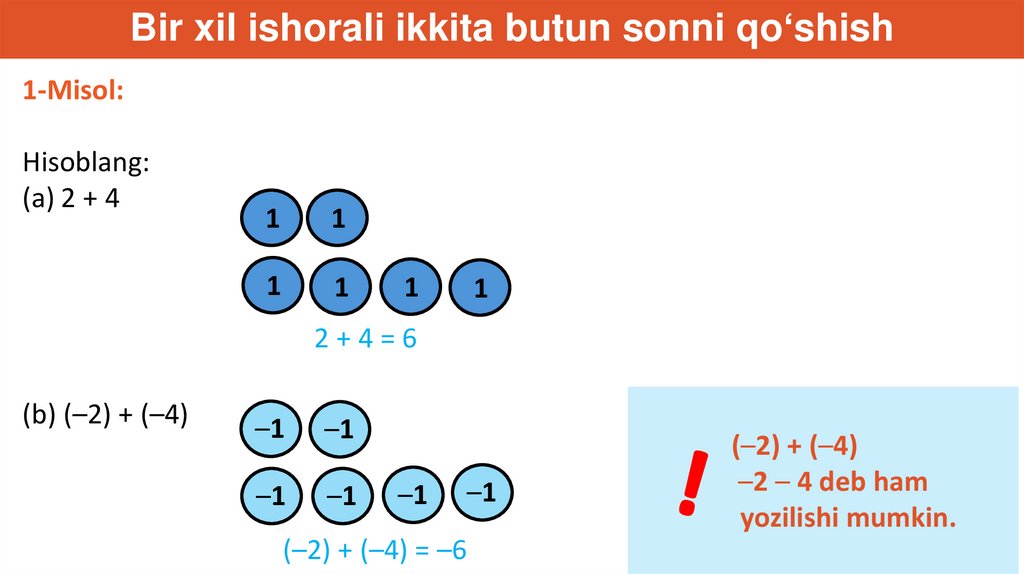
Bir xil ishorali ikkita butun sonni qo‘shish
1-Misol:
Hisoblang:
(a) 2 + 4
1
1
1
1
1
1
2+4=6
(b) (–2) + (–4)
© All rights reserved
–1
–1
–1
–1
–1
–1
(–2) + (–4) = –6
(–2) + (–4)
–2 – 4 deb ham
yozilishi mumkin.

18.

Keling, sinab ko‘ramiz!
(–2) + (–5) ni hisoblang?
Javob berish uchun algebraik va
sonli tugmalardan foydalaning.
Source: Used with permission – Microsoft Stoc

19.

Turli ishorali ikkita butun sonni
qo‘shish
Source: Used with permission – Microsoft Stoc

20.

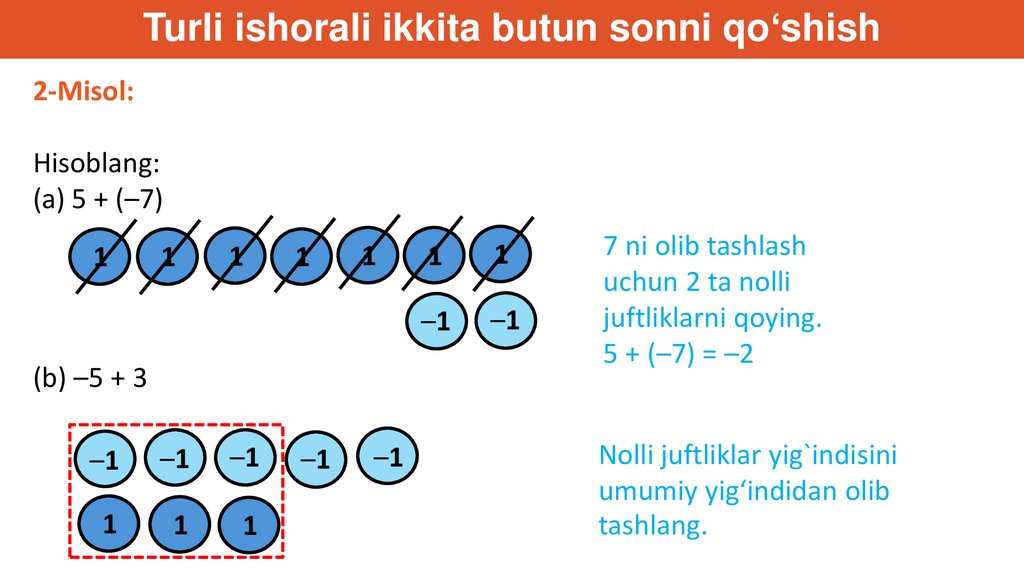
Turli ishorali ikkita butun sonni qo‘shish
2-Misol:
Hisoblang:
(a) 5 + (–7)
1
1
1
1
1
(b) –5 + 3
–1
–1
–1
1
1
1
–1
–1
1
1
–1
–1
7 ni olib tashlash
uchun 2 ta nolli
juftliklarni qoying.
5 + (–7) = –2
Nolli juftliklar yig`indisini
umumiy yig‘indidan olib
tashlang.

21.

Keling, sinab ko‘ramiz!
3 + (–4) ni hisoblang?
Javob berish uchun algebraik va
sonli tugmalardan foydalaning.
5 min
Source: Used with permission – Microsoft Stoc

22.

Musbat butun sonni ayirish
Source: Used with permission – Microsoft Stoc

23.

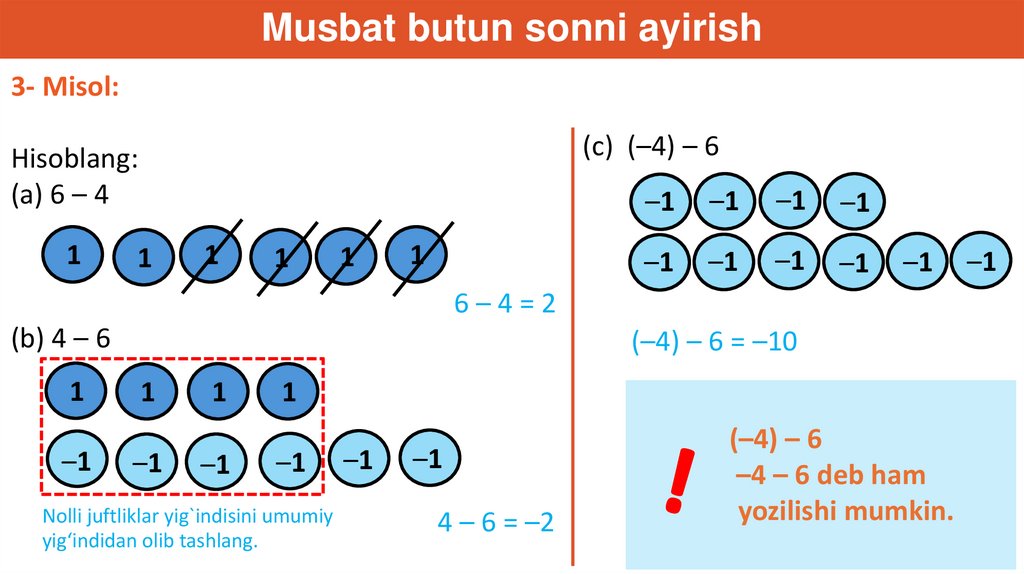
Musbat butun sonni ayirish
3- Misol:
(c) (–4) – 6
Hisoblang:
(a) 6 – 4
1
1
1
1
1
1
–1
–1
–1
–1
–1
–1
–1
–1
–1
6–4=2
(b) 4 – 6
1
–1
(–4) – 6 = –10
1
–1
1
–1
1
–1
Nolli juftliklar yig`indisini umumiy
yig‘indidan olib tashlang.
–1
–1
4 – 6 = –2
(–4) – 6
–4 – 6 deb ham
yozilishi mumkin.
–1

24.

Keling, sinab ko‘ramiz!
2 – 6 ni hisoblang?
Javob berish uchun algebraik va
sonli tugmalardan foydalaning.
5 min
Source: Used with permission – Microsoft Stoc

25.

Manfiy butun sonni ayirish

26.

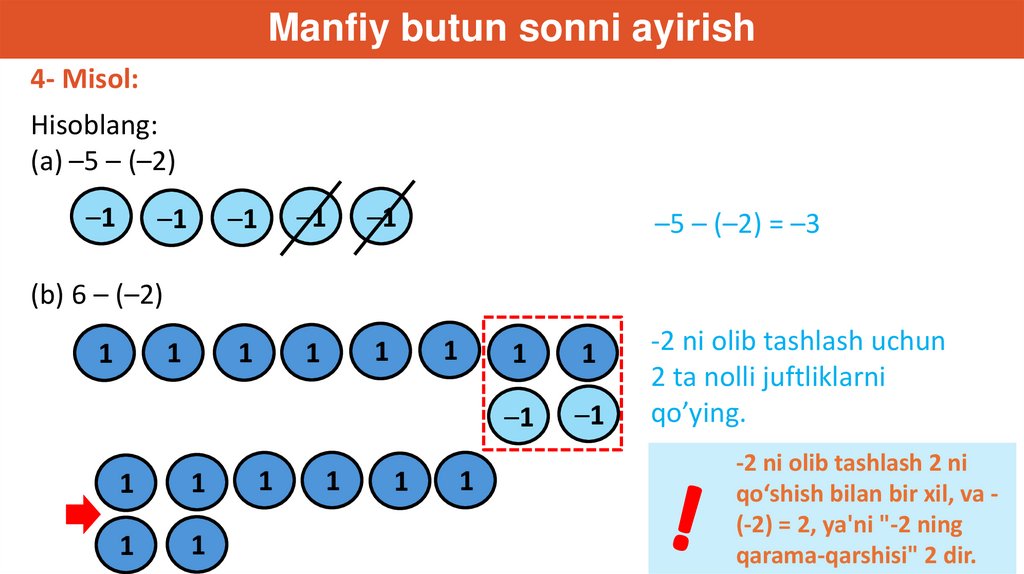
Example 4
Manfiy butun sonni ayirish
4- Misol:
Hisoblang:
(a) –5 – (–2)
–1
–1
–1
–1
–1
1
1
1
–5 – (–2) = –3
(b) 6 – (–2)
1
1
1
1
1
1
1
1
1
1
1
1
1
–1
–1
-2 ni olib tashlash uchun
2 ta nolli juftliklarni
qo’ying.
-2 ni olib tashlash 2 ni
qo‘shish bilan bir xil, va (-2) = 2, ya'ni "-2 ning
qarama-qarshisi" 2 dir.

27.

Keling, sinab ko‘ramiz!
5 – (–7) ni hisoblang?
Javob berish uchun algebraik va
sonli tugmalardan foydalaning.
5 min
Source: Used with permission – Microsoft Stoc

28.

Tanaffus
Source: Used with permission – Microsoft Stoc

29.

Butun sonlarni ko‘paytirish
Source: Used with permission – Microsoft Stoc

30.

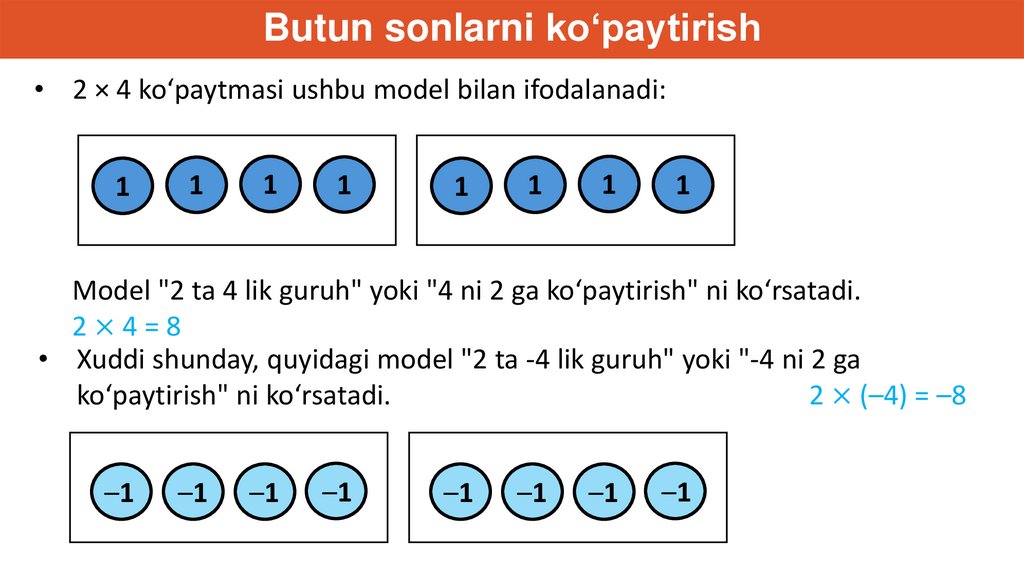
Butun sonlarni ko‘paytirish
• 2 × 4 ko‘paytmasi ushbu model bilan ifodalanadi:
1
1
1
1
1
1
1
1
Model "2 ta 4 lik guruh" yoki "4 ni 2 ga ko‘paytirish" ni ko‘rsatadi.
2×4=8
• Xuddi shunday, quyidagi model "2 ta -4 lik guruh" yoki "-4 ni 2 ga
ko‘paytirish" ni ko‘rsatadi.
2 × (–4) = –8
–1
–1
–1
–1
–1
–1
–1
–1

31.

Butun Sonlarni Ko‘paytirish
• Keling, quyidagilarning har birida topilgan o`zaro bog`liqlikni ko‘rib
chiqaylik:
(B)
(A)
3 × (–4) = –12
3 × 4 = 12
2 × (–4) = –8
2×4=8
1 × (–4) = –4
1×4=4
0 × (–4) = 0
0×4=0
(–1) × (–4) = ?
(–1) × 4 = ?
(–2) × (–4) = ?
(–2) × 4 = ?
(–3) × (–4) = ?
(–3) × 4 = ?
(A) dagi bog`liqlik shuni ko‘rsatadiki, (-1) × 4 = -4.
(B) dagi bog`liqlik shuni ko‘rsatadiki, (-1) × (-4) = 4.

32.

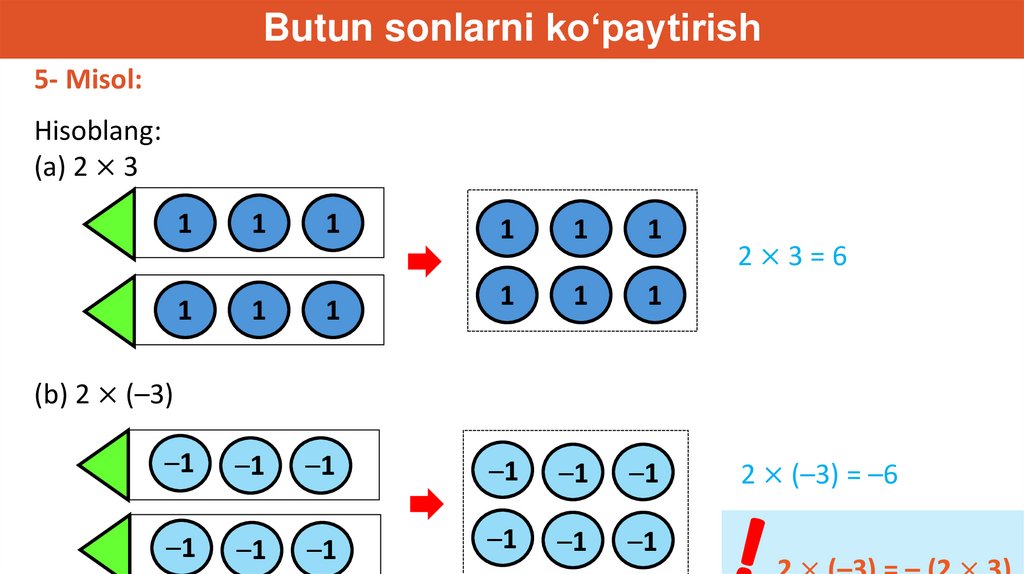
Butun sonlarni ko‘paytirish
5- Misol:
Hisoblang:
(a) 2 × 3
1
1
1
1
1
1
1
1
1
1
1
1
–1
–1
–1
–1
–1
–1
2×3=6
(b) 2 × (–3)
- –1 –1 –1
- –1 –1 –1
2 × (–3) = –6

33.

Keling, qo‘llab ko‘ramiz!
2 × (–4) ko’paytmani hisoblang?
Javob berish uchun algebraik va
sonli tugmalardan foydalaning.
Source: Used with permission – Microsoft Stoc

34.

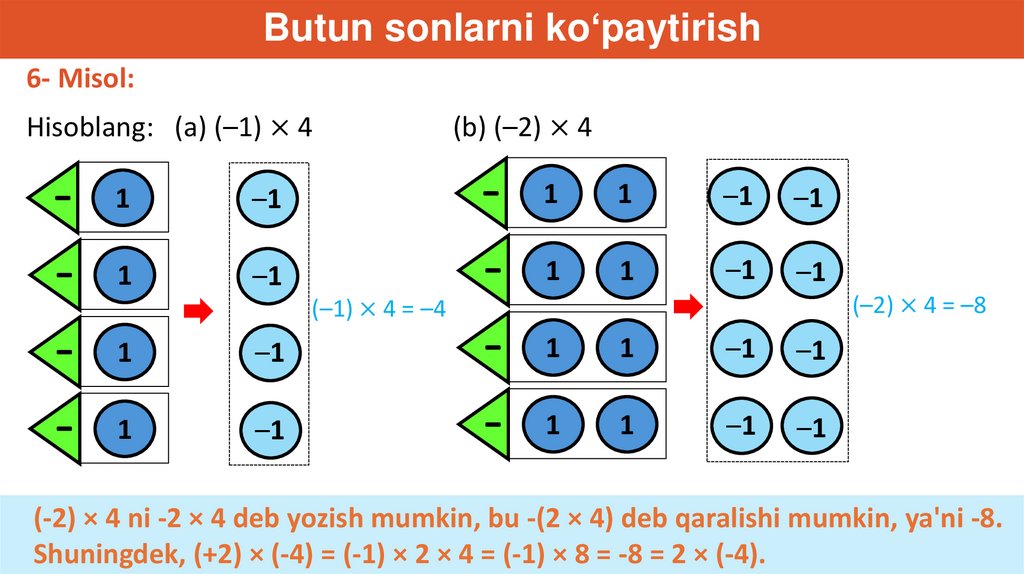
Butun sonlarni ko‘paytirish
6- Misol:
Hisoblang: (a) (–1) × 4
- 1
- 1
- 1
- 1
(b) (–2) × 4
- 1
1
–1
(–1) × 4 = –4
–1
- 1
–1
- 1
–1
1
–1
–1
1
–1
–1
(–2) × 4 = –8
1
–1
–1
1
–1
–1
(-2) × 4 ni -2 × 4 deb yozish mumkin, bu -(2 × 4) deb qaralishi mumkin, ya'ni -8.
Shuningdek, (+2) × (-4) = (-1) × 2 × 4 = (-1) × 8 = -8 = 2 × (-4).

35.

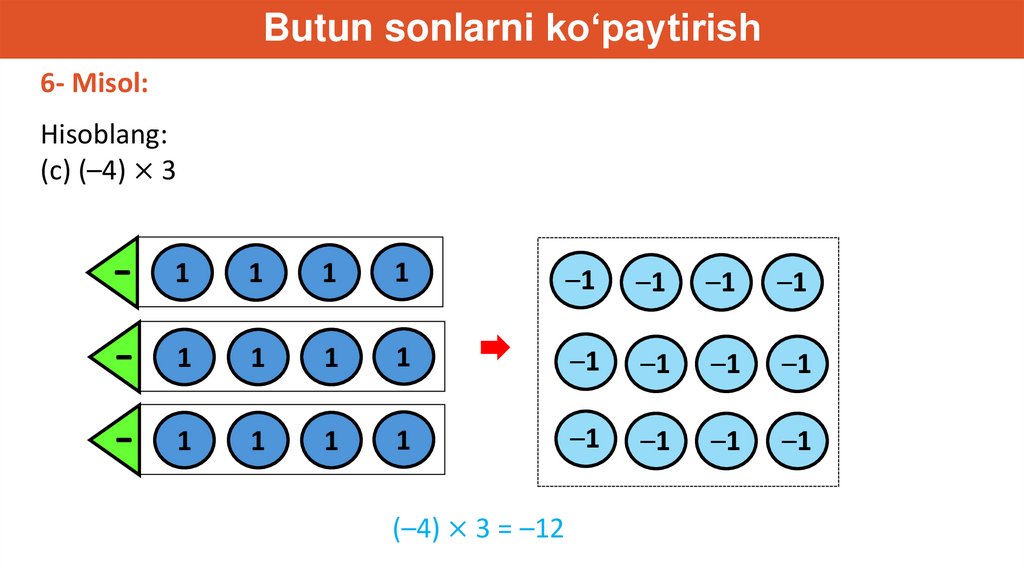
Butun sonlarni ko‘paytirish
6- Misol:
Hisoblang:
(c) (–4) × 3
- 1
- 1
- 1
1
1
1
–1
–1
–1
–1
1
1
1
–1
–1
–1
–1
1
1
1
–1
–1
–1
–1
(–4) × 3 = –12

36.

Keling, qo‘llab ko‘ramiz!
(–3) × 3 ni hisoblang?
Javob berish uchun algebraik va
sonli tugmalardan foydalaning.
Source: Used with permission – Microsoft Stoc

37.

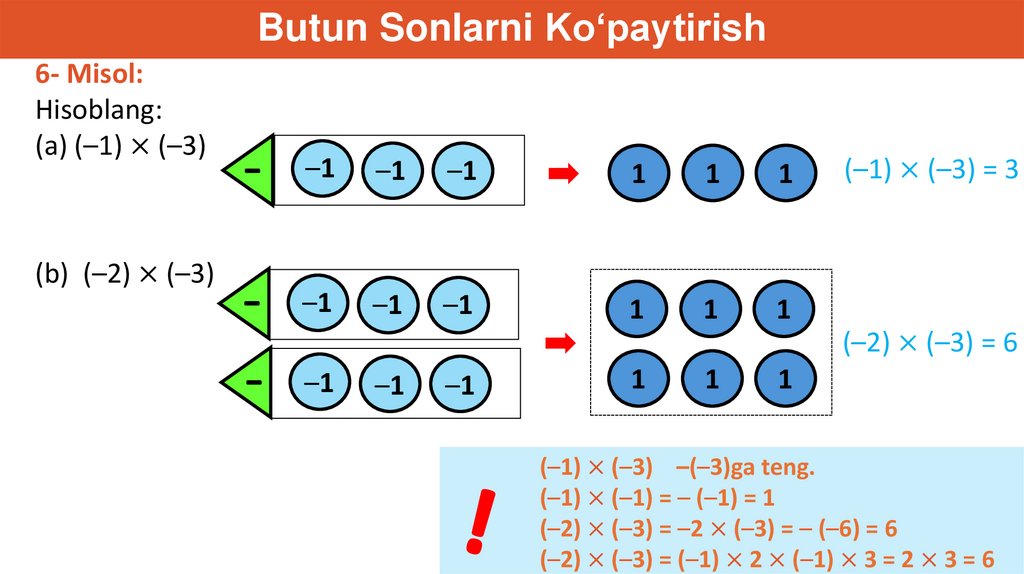
Butun Sonlarni Ko‘paytirish
6- Misol:
Hisoblang:
(a) (–1) × (–3)
(b) (–2) × (–3)
- –1 –1 –1
- –1 –1 –1
- –1 –1 –1
1
1
1
1
1
1
(–1) × (–3) = 3
(–2) × (–3) = 6
1
1
1
(–1) × (–3) –(–3)ga teng.
(–1) × (–1) = – (–1) = 1
(–2) × (–3) = –2 × (–3) = – (–6) = 6
(–2) × (–3) = (–1) × 2 × (–1) × 3 = 2 × 3 = 6

38.

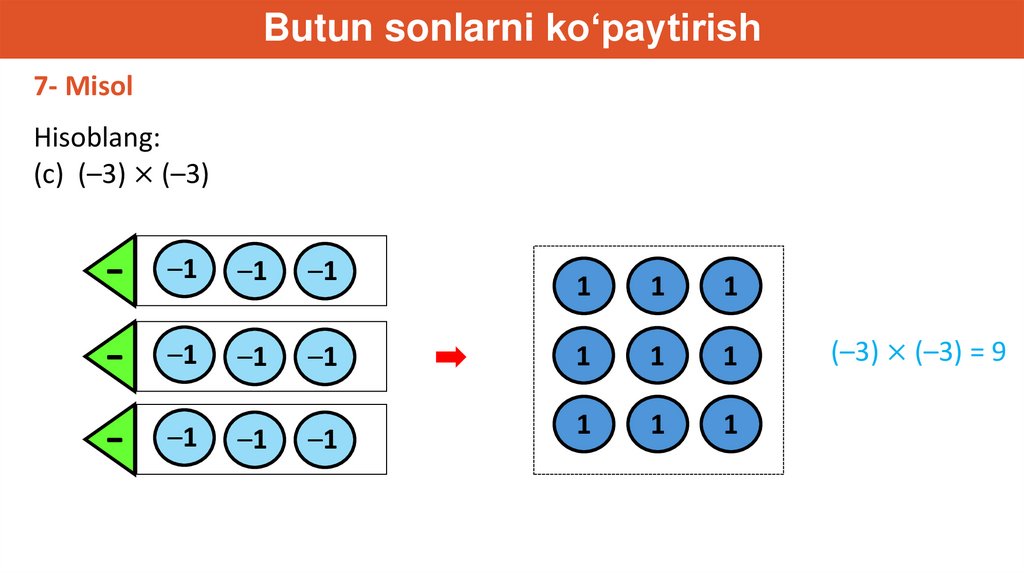
Butun sonlarni ko‘paytirish
7- Misol
Hisoblang:
(c) (–3) × (–3)
- –1 –1 –1
- –1 –1 –1
- –1 –1 –1
1
1
1
1
1
1
1
1
1
(–3) × (–3) = 9

39.

Keling, qo’llab ko‘ramiz!
(–3) × (–4) ni hisoblang?
Javob berish uchun algebraik va
sonli tugmalardan foydalaning.
Source: Used with permission – Microsoft Stoc

40.

Algebraik Ifodalar
Source: Used with permission – Microsoft Stoc

41.

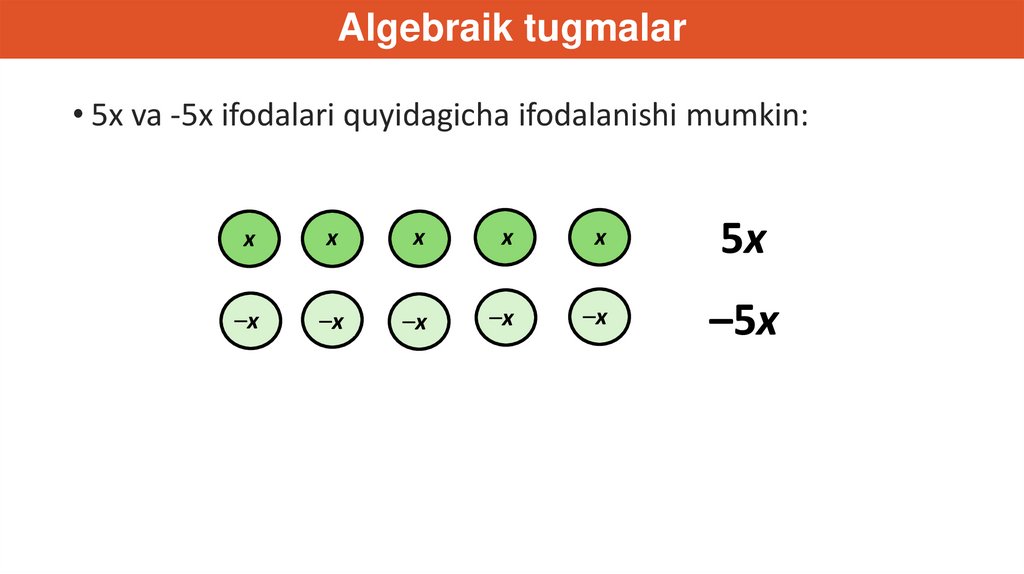
Algebraik tugmalar
• 5x va -5x ifodalari quyidagicha ifodalanishi mumkin:
x
x
x
x
x
5x
–x
–x
–x
–x
–x
–5x

42.

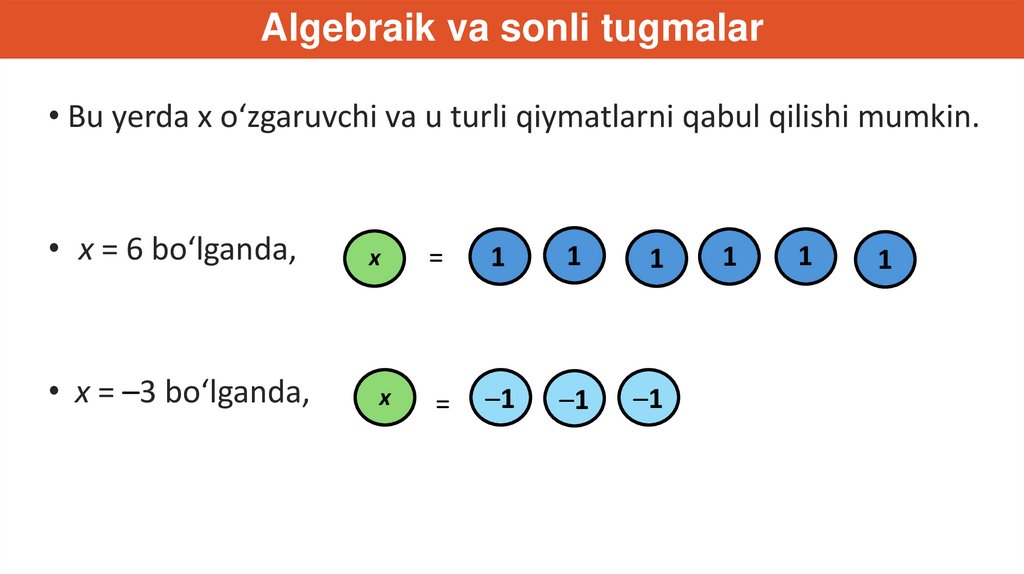
Algebraik va sonli tugmalar
• Bu yerda x o‘zgaruvchi va u turli qiymatlarni qabul qilishi mumkin.
• x = 6 bo‘lganda,
x
=
1
1
1
• x = –3 bo‘lganda,
x
=
–1
–1
–1
1
1
1

43.

Algebra va Sonli tugmalar
x
va
1
kabi tugmalar algebraik tugmalar deb ataladi
• Har bir tugmaning quyida ko‘rsatilganidek ikkita tomoni bor, :
x
–x
1
–1
old
orqa
old
orqa
• Biz tugmani aylantirib, uning old yoki orqa tomonini
ko‘rsatishimiz mumkin.

44.

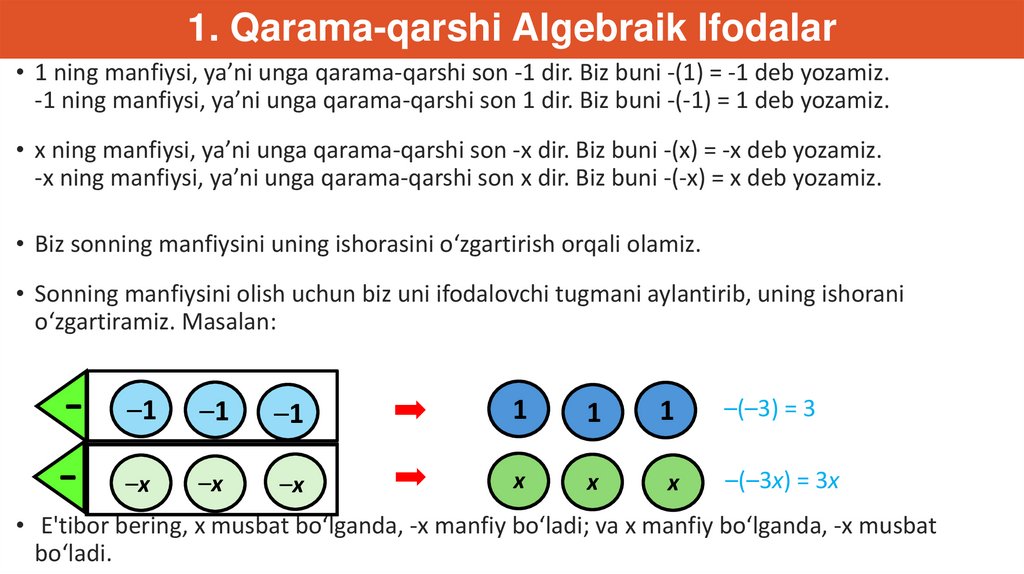
1. Qarama-qarshi Algebraik Ifodalar
• 1 ning manfiysi, ya’ni unga qarama-qarshi son -1 dir. Biz buni -(1) = -1 deb yozamiz.
-1 ning manfiysi, ya’ni unga qarama-qarshi son 1 dir. Biz buni -(-1) = 1 deb yozamiz.
• x ning manfiysi, ya’ni unga qarama-qarshi son -x dir. Biz buni -(x) = -x deb yozamiz.
-x ning manfiysi, ya’ni unga qarama-qarshi son x dir. Biz buni -(-x) = x deb yozamiz.
• Biz sonning manfiysini uning ishorasini o‘zgartirish orqali olamiz.
• Sonning manfiysini olish uchun biz uni ifodalovchi tugmani aylantirib, uning ishorani
o‘zgartiramiz. Masalan:
- –1 –1 –1
–x
–x
–x
1
1
1
–(–3) = 3
x
x
x
–(–3x) = 3x
• E'tibor bering, x musbat bo‘lganda, -x manfiy bo‘ladi; va x manfiy bo‘lganda, -x musbat
bo‘ladi.

45.

2. Yig`indisi nolga teng nolli jurtliklar
• -1 manfiy butun soni shunday sonki, 1 + (-1) = 0. 1 va -1 ni nolli jurtliklar deb ataymiz.
• Umuman olganda, x soni va uning –x manfiysi nolli jurtlikni hosil qiladi, ya'ni x + (-x) = 0.
• Nolli jurtliklarga misollar:
(a) 2 + (–2) = 0
(b) 3x + (–3x) = 0
1
1
x
x
x
–1
–1
–x
–x
–x

46.

Chiziqli Ifodalar
Source: Used with permission – Microsoft Stoc

47.

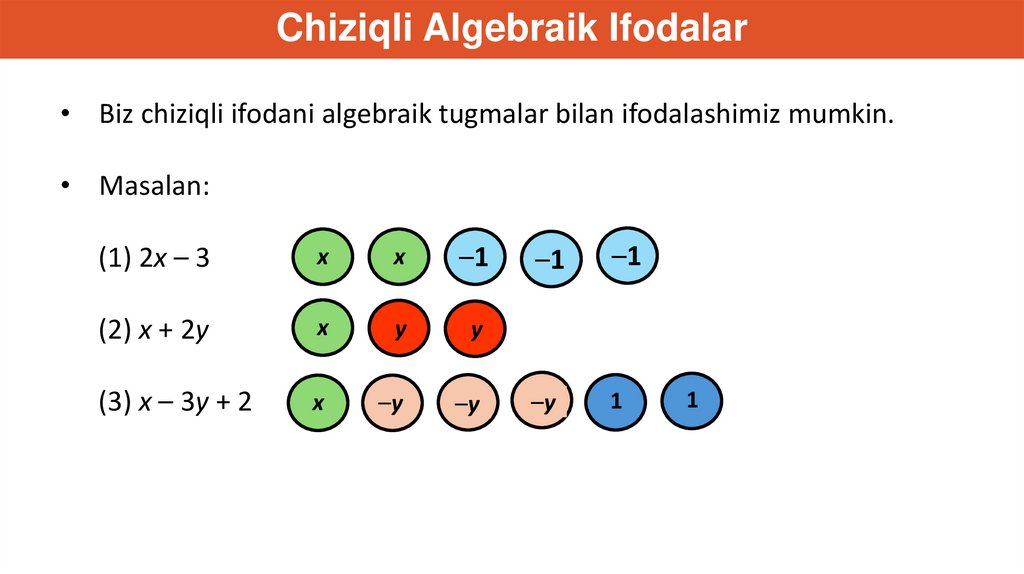
Chiziqli Algebraik Ifodalar
• Biz chiziqli ifodani algebraik tugmalar bilan ifodalashimiz mumkin.
• Masalan:
(1) 2x – 3
x
x
–1
(2) x + 2y
x
y
y
(3) x – 3y + 2
x
–y
–y
–1
–1
–y
1
1

48.

Algebraik ifodaning qaramaqarshisini topish
Source: Used with permission – Microsoft Stoc

49.

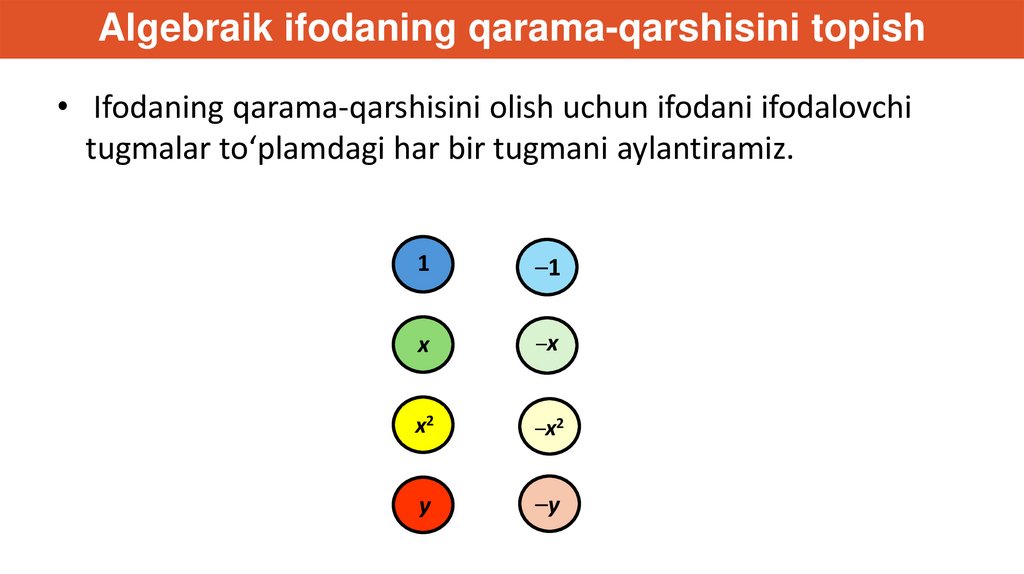
Algebraik ifodaning qarama-qarshisini topish
• Ifodaning qarama-qarshisini olish uchun ifodani ifodalovchi
tugmalar to‘plamdagi har bir tugmani aylantiramiz.
1
–1
x
–x
x2
–x2
y
–y

50.

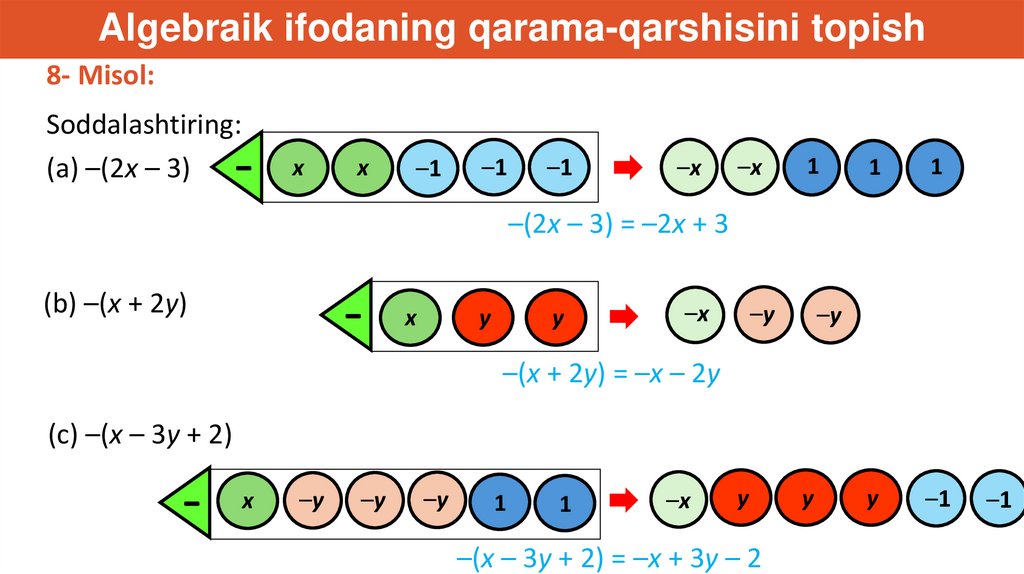
Algebraik ifodaning qarama-qarshisini topish
8- Misol:
Soddalashtiring:
(a) –(2x – 3)
-
x
x
–1
–1
–1
–x
–x
1
–y
–y
1
1
y
–1
–(2x – 3) = –2x + 3
-
(b) –(x + 2y)
x
y
y
–x
–(x + 2y) = –x – 2y
(c) –(x – 3y + 2)
-
x
–y
–y
–y
1
1
–x
y
–(x – 3y + 2) = –x + 3y – 2
y
–1

51.

Keling, qo‘llab ko‘ramiz!
Soddalashtiring:
(a) –(x + 1)
(b) –(x – 1)
(c) –(–x + 1)
(d) –(–x – 1)
Javob berish uchun algebraik va
sonli tugmalardan foydalaning.
Source: Used with permission – Microsoft Stoc

52.

Keling, qo‘llab ko‘ramiz!
Soddalashtiring:
(a) –(x + y)
(b) –(x – y)
(c) –(–x + y)
(d) –(–x – y)
Javob berish uchun algebraik va
sonli tugmalardan foydalaning.
Source: Used with permission – Microsoft Stoc

53.

Keling, qo‘llab ko‘ramiz!
Soddalashtiring:
(a) –(3x – 2)
(b) –(–2x – 3)
(c) –(–3x + 2y)
(d) –(2x – 3y + 1)
Javob berish uchun algebraik va sonli
tugmalardan foydalaning.
Source: Used with permission – Microsoft Stoc

54.

Tanaffus
Source: Used with permission – Microsoft Stoc

55.

Birhadlarni qo‘shish va ayirish
Source: Used with permission – Microsoft Stoc

56.

Birhadlarni qo‘shish va ayirish
• Birhadlarni qo‘shish va ayirishni tasvirlash uchun algebraik
tugmalardan foydalanamiz, bu yerda a butun son va x
o‘zgaruvchidir.

57.

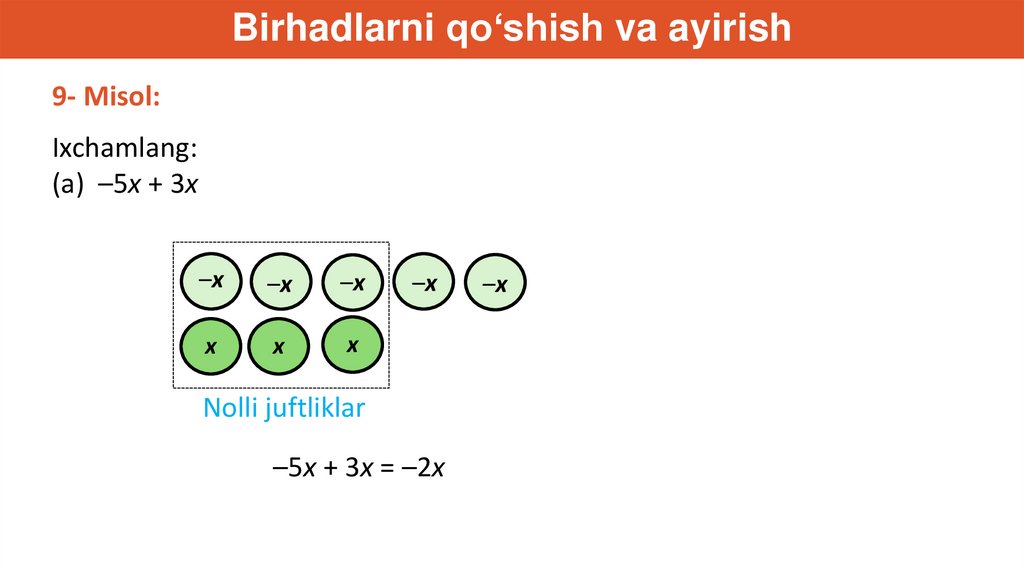
Birhadlarni qo‘shish va ayirish
9- Misol:
Ixchamlang:
(a) –5x + 3x
–x
–x
–x
x
x
x
–x
Nolli juftliklar
–5x + 3x = –2x
–x

58.

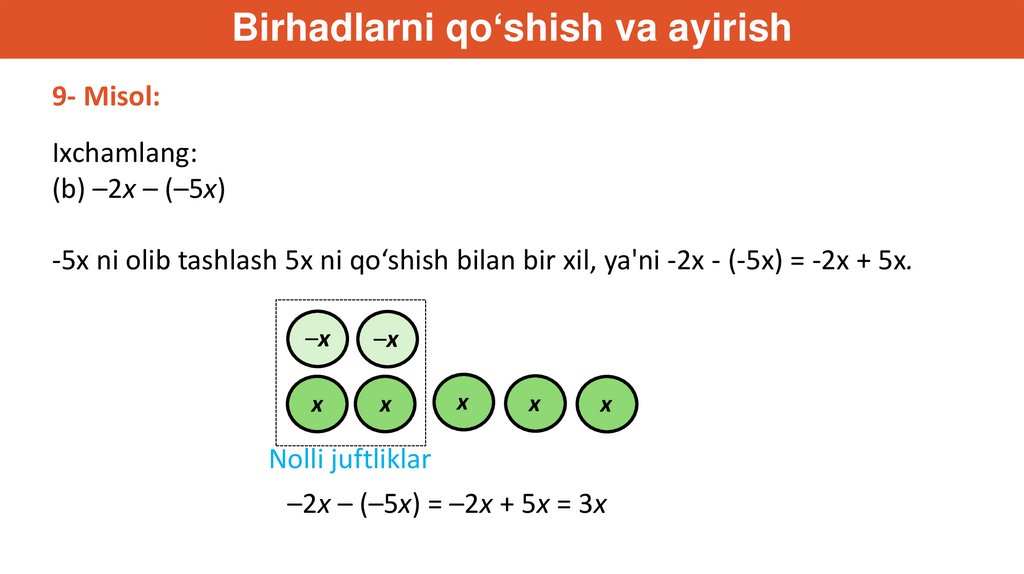
Birhadlarni qo‘shish va ayirish
9- Misol:
Ixchamlang:
(b) –2x – (–5x)
-5x ni olib tashlash 5x ni qo‘shish bilan bir xil, ya'ni -2x - (-5x) = -2x + 5x.
–x
–x
x
x
x
x
x
Nolli juftliklar
–2x – (–5x) = –2x + 5x = 3x

59.

Keling, sinab ko‘ramiz!
Soddalashtiring:
(a) 3x + 4x
(b) 3x – 4x
(c) –3x + 4x
(d) –3x – 4x
Javob berish uchun algebraik va
sonli tugmalardan foydalaning.
Source: Used with permission – Microsoft Stoc

60.

Keling, sinab ko‘ramiz!
Soddalashtiring:
(a) 3x + (–4x)
(b) 3x – (–4x)
(c) –3x + (–4x)
(d) –3x – (–4x)
Javob berish uchun algebraik va
sonli tugmalardan foydalaning.
Source: Used with permission – Microsoft Stoc

61.

O‘xshash hadlarni ixchamlash
Source: Used with permission – Microsoft Stoc

62.

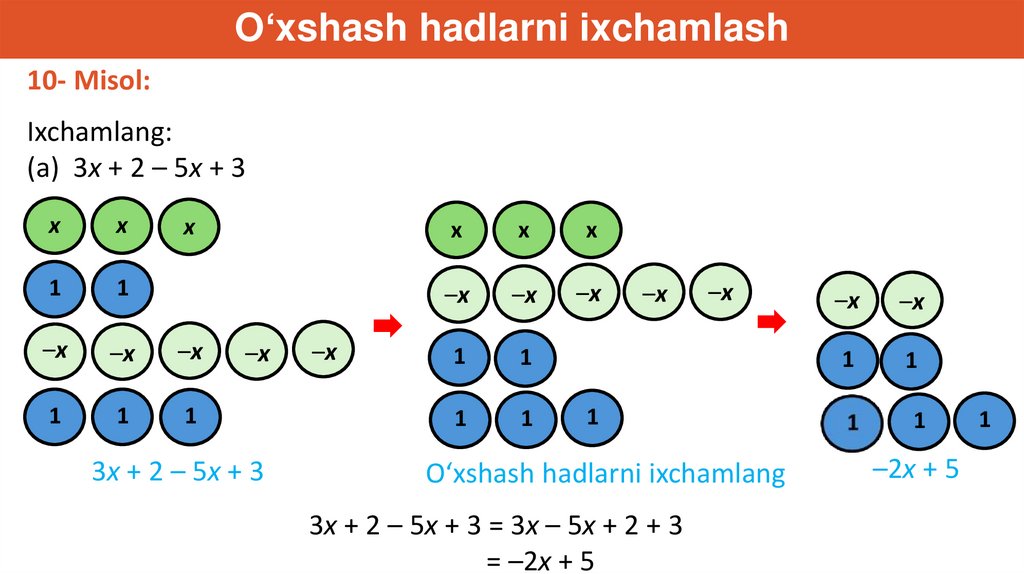
O‘xshash hadlarni ixchamlash
10- Misol:
Ixchamlang:
(a) 3x + 2 – 5x + 3
x
x
1
1
–x
–x
–x
1
1
1
x
–x
3x + 2 – 5x + 3
–x
x
x
x
–x
–x
–x
1
1
1
1
–x
–x
–x
–x
1
1
1
1
O‘xshash hadlarni ixchamlang
–2x + 5
3x + 2 – 5x + 3 = 3x – 5x + 2 + 3
= –2x + 5
1

63.

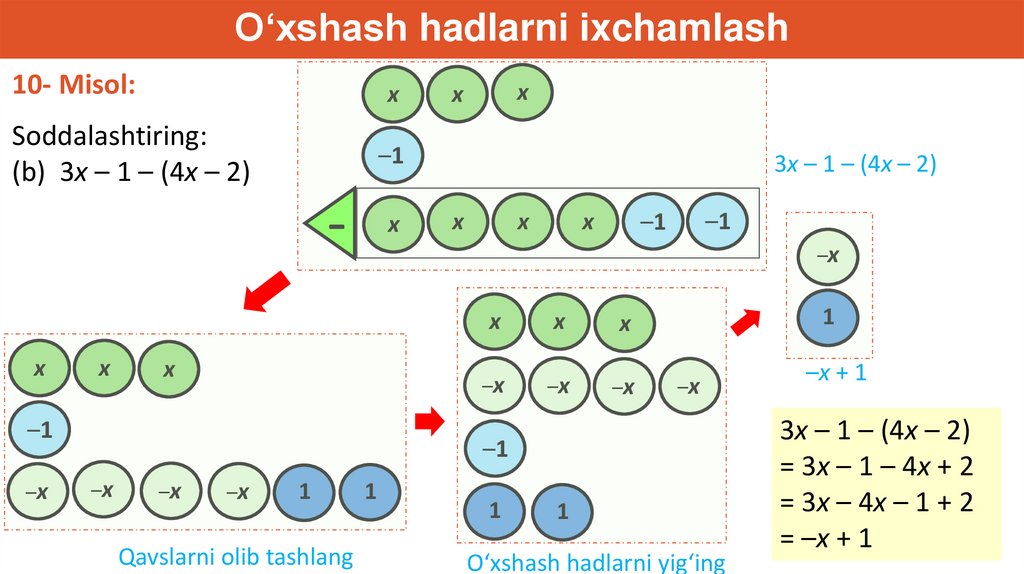
O‘xshash hadlarni ixchamlash
10- Misol:
x
Soddalashtiring:
(b) 3x – 1 – (4x – 2)
–1
x
x
x
3x – 1 – (4x – 2)
x
x
–1
–1
x
–x
x
–1
–x
x
x
x
x
x
–x
–x
–x
1
–x
–1
–x
–x
–x
1
Qavslarni olib tashlang
1
1
1
O‘xshash hadlarni yig‘ing
–x + 1
3x – 1 – (4x – 2)
= 3x – 1 – 4x + 2
= 3x – 4x – 1 + 2
= –x + 1

64.

Algebraik ifodalarni butun songa
ko‘paytirish
Source: Used with permission – Microsoft Stoc

65.

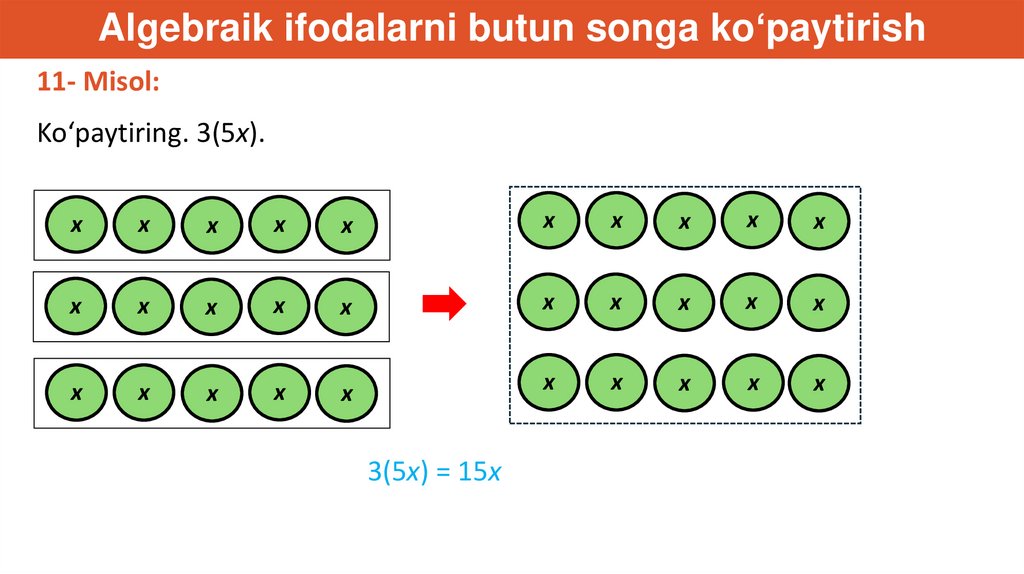
Algebraik ifodalarni butun songa ko‘paytirish
11- Misol:
Ko‘paytiring. 3(5x).
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
3(5x) = 15x

66.

Keling, qo’llab ko‘ramiz!
• Ko‘paytiring:
(a) 2(–2x)
Javob berish uchun algebraik va
sonli tugmalardan foydalaning.
Source: Used with permission – Microsoft Stoc

67.

Keling, qo’llab ko‘ramiz!
Ko‘paytiring:
(b) –3(–2x)
Javob berish uchun algebraik va
sonli tugmalardan foydalaning.
Source: Used with permission – Microsoft Stoc

68.

Chiziqli tenglamalarni yechish
Source: Used with permission – Microsoft Stoc

69.

Chiziqli tenglamalarni yechish
• Chiziqli tenglamalarni yechish jarayonini tasvirlash uchun
algebraik tugmalardan foydalanamiz.

70.

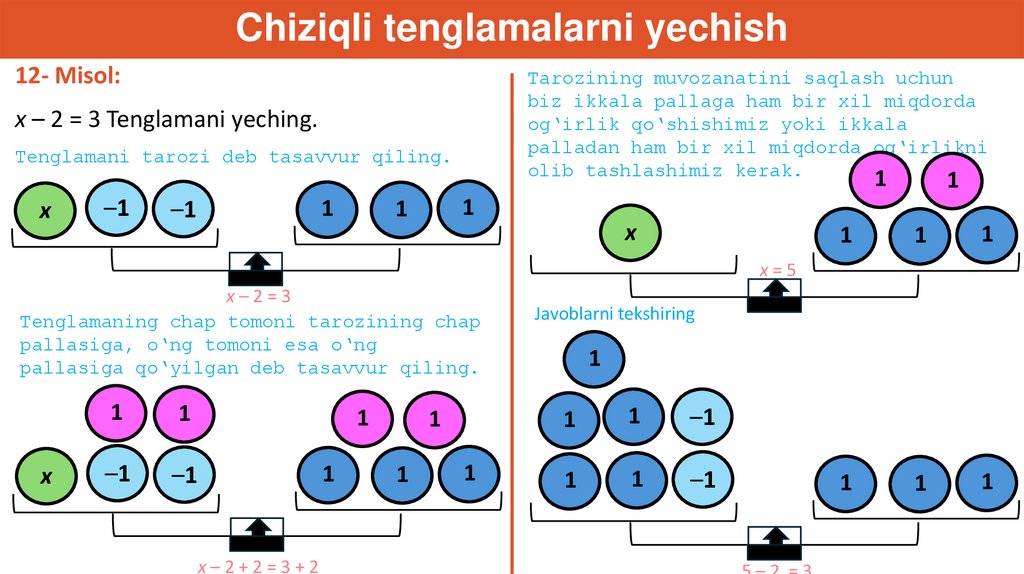
Chiziqli tenglamalarni yechish
12- Misol:
Tarozining muvozanatini saqlash uchun
biz ikkala pallaga ham bir xil miqdorda
og‘irlik qo‘shishimiz yoki ikkala
palladan ham bir xil miqdorda og‘irlikni
olib tashlashimiz kerak.
x – 2 = 3 Tenglamani yeching.
Tenglamani tarozi deb tasavvur qiling.
1
x
–1
1
–1
1
1
1
x
1
1
1
1
1
1
x=5
x–2=3
Tenglamaning chap tomoni tarozining chap
pallasiga, o‘ng tomoni esa o‘ng
pallasiga qo‘yilgan deb tasavvur qiling.
x
1
1
–1
–1
1
x–2+2=3+2
1
1
1
1
Javoblarni tekshiring
1
1
1
–1
1
1
–1

71.

Keling, qo’llab ko‘ramiz!
Tenglamani yeching:
(a) 2x + 3 = 1
Javob berish uchun algebraik va
sonli tugmalardan foydalaning.
Source: Used with permission – Microsoft Stoc

72.

Keling, qo’llab ko‘ramiz!
Tenglamani yeching:
(b) 3x – 2 = –2x + 1
Javob berish uchun algebraik va
sonli tugmalardan foydalaning.
Source: Used with permission – Microsoft Stoc

73.

Tanaffus
Source: Used with permission – Microsoft Stoc

74.

Mustahkamlash
Source: Used with permission – Microsoft Stoc

75.

Ortga nazar – tushunchalarini qo‘llash
• O‘qitishni amaliyotga tadbiq etish
• Bugungi mavzuyimiz o‘qituvchilarni tayyorlashga qanday ta'sir qilishini o‘rganing.
• Mulohaza yuritish uchun savollar:
• Bugun o‘rgangan eng muhim uchta tushuncha yoki strategiya qaysilar?
• Bu tushunchalar matematika o‘qitish va o‘rganish haqidagi hozirgi qarashlaringizga qanchalik
qarshi yoki mos keladi?
• Bugungi muhokamalar yoki mashg‘ulotlar davomida siz uchun eng “ajoyib" lahza qaysi bo‘ldi?
• Faoliyat (O‘ylang-yozing-mulohaza qiling-baham ko‘ring):
• O‘ylang: Javoblaringizni yozib olish uchun 5 daqiqa vaqt ajrating.
• Mulohaza qiling: Fikrlaringizni yoningizdagi sherigingiz bilan muhokama qiling.
• Baham ko‘ring: Stol atrofidagi guruh sifatida fikrlarni birlashtiring va qolganlar bilan baham
ko‘rish uchun umumiy xulosa chiqaring.

76.

Oldinga nazar – tushunchalarini qo‘llash
• Yo‘naltiruvchi savollar:
• Ushbu strategiyalarni tumaningizdagi o‘qituvchilar bilan baham ko‘rishda qanday
qiyinchiliklarga uchrash mumkin deb o`ylaysiz?
• Bugungi mashg’ulotdagi qaysi misollar, vositalar yoki o‘xshatishlar o‘qituvchilarga bu
tushunchalarni samaraliroq tushunishga yordam berishi mumkin?
• Bugungi o`rganganlaringizni o‘quv rejalaringizga kiritish uchun qanday aniq harakatlar
qilasiz?
• Keyingi qadamlar (individual ish):
• O‘qituvchilaringizga bitta tushuncha yoki strategiyani (masalan, Frayer modelini) qanday
tanishtirishingiz mumkinligi haqida qisqacha reja tuzing.
• Un kontseptual tushunishni qanday qo‘llab-quvvatlashini yoki o‘qitishdagi umumiy
muammolarni qanday hal qilishi mumkinligiga aniqlik kiriting.

77.

Guruh Taqdimotlari

78.

Bugungi sessiyaning maqsadlari
Ishtirokchilarning matematikada tushuncha va bosqichmabosqich ishlash qobiliyatini oshirish maqsadida amaliy
mashg’ulotlar va vizual ifodalardan foydalanish orqali ishlash.
Venn diagrammalari, daraxt diagrammalari va kontseptual
xaritalar kabi turli xil grafik vositlarning matematik
munosabatlar va tushunchalarni muloqotda hamda
mustahkamlashda qo‘llanilishi.
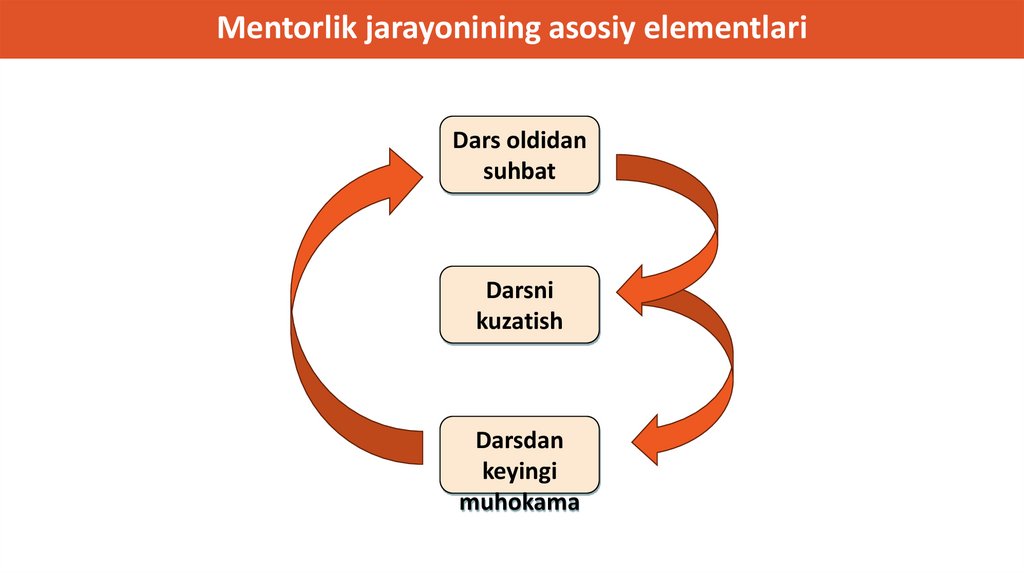
Matematika o‘qituvchilarini qo‘llab-quvvatlash uchun
samarali mentorlik ko‘nikmalarini rivojlantirish, jumladan,
o‘rgatishdan oldin muhokamalar o‘tkazish, o‘quv jarayonini
kuzatish va darsdandan keyin tahlillar o‘tkazish.
Source: Used with permission – Microsoft Stock Image

79.

1-Mashg‘ulot
Source: Used with permission – Microsoft Stoc

80.

1-Mashg‘ulot – Uchburchak
Materials Required:
• Six tayoqchalar
• Tayoqchalar uzunligini o'lchash uchun o‘lchagich
• Tayoqchalarni joylashtirish uchun tekis sirt

81.

Ko'rsatmalar
1. Tayyorlanishi
• Belgilangan uzunlikdagi 3 ta tayoqchani kesib oling: 5 sm, 8 sm va 10 sm
• Tayoqchalar kerakli uzunliklarga to'g'ri o'lchanganligiga ishonch hosil qiling.
2. Uchburchak tuzulishi
• Uchburchak hosil qilish uchun tayoqchalardan foydalaning. tayoqchachalarni
so'nggi nuqtalari bir-biriga to'g'ri kelmasdan to'liq mos keladigan tarzda
joylashtiring.
• Bir xil tayoqchaning bir nechta joylashuvi turli uchburchaklar hosil qilishini
tekshiring.
Masalan:
• Uchburchakni aylantirish yoki o‘girishga harakat qiling.
• Ko‘rinishi o‘zgarmaganligiga ishonch hosil qiling (aynan shunday bo‘lsin).

82.

Ko‘rsatmalar
3. Berilgan uchburchak bilan solishtirish
Siz yaratgan uchburchak berilgan uchburchakka mos keladimi
(tarqatma materialga qarang)?

83.

Ko‘rsatmalar
4. Boshqa uzunliklar bilan takrorlang
• Turli uzunlikdagi uchta yangi tayoqchani tanlang.
• Uchburchak hosil qiling va har doim boshqa uchburchak hosil bo‘lganini
tekshiring.
Qo'shimcha o'rganish uchun
• Ba’zi o‘quvchilar uchburchakning 3 tomonining ixtiyoriy uzunliklarini
tanlaydilar va ular uchburchak hosil qila olmasligini tushunadilar.
• Muhokama uchun: Uchburchak tomonlari tengsizligi - Agar 2 ta qisqa
tayoqchaning uzunliklari yig‘indisi eng uzun tayoqcha uzunligidan kichik yoki
teng bo'lsa, uchburchak hosil bo‘lmaydi.
• O‘quvchilar buni tayoqchalarda tekshirishlariga undang.

84.

Tajribadan olingan xulosalar
• Agar uchburchakning 3 tomoni ham boshqa uchburchakning 3 tomoni
bilan bir xil bo‘lsa, u holda ikki uchburchak mos uchburchaklar bo‘ladi.
• Bu yerda 3ta juft mos burchak bo'ladi.
• Ikki uchburchakning 3 juft teng mos tomonlari bo'lsa, ular tomonlari (TTT)
mosligi asosida mos uchburchaklar hisoblanadi.

85.

Ushbu binoning
balandligini
aniqlash uchun
trigonometriyadan
qanday
foydalanishimiz
mumkin ?

86.

2-Mashg‘ulot
Source: Used with permission – Microsoft Stoc

87.

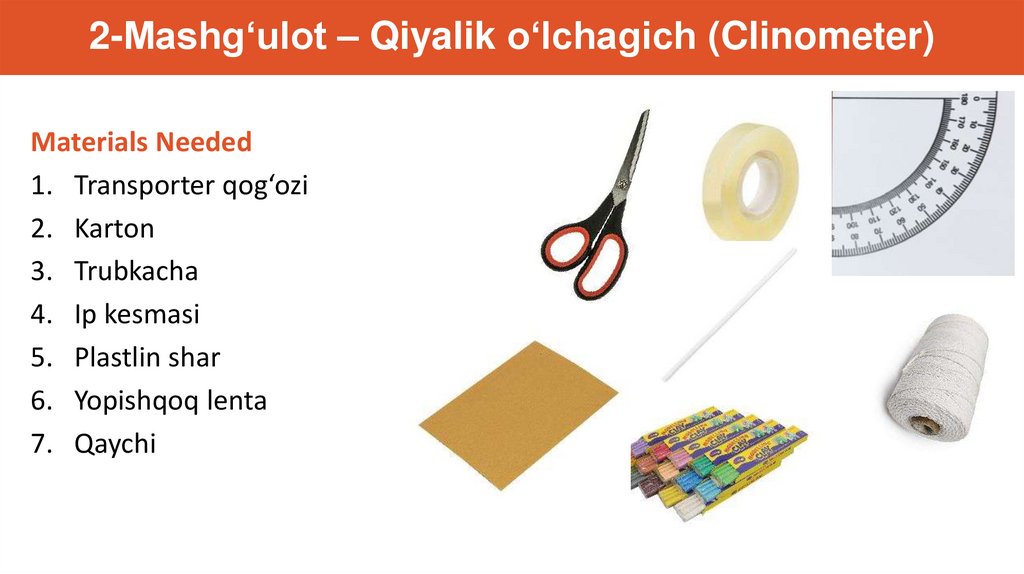
2-Mashg‘ulot – Qiyalik o‘lchagich (Clinometer)
Materials Needed
1. Transporter qog‘ozi
2. Karton
3. Trubkacha
4. Ip kesmasi
5. Plastlin shar
6. Yopishqoq lenta
7. Qaychi

88.

Qiyalik o‘lchagich yarating (Clinometer)
Make a
hole here.
1-qadam: Transpartir tayyorlang.
• Yelim yordamida karton varaq ustiga
transpartyorni yopishtiring. Uning tekis va
mahkam biriktirilganligiga ishonch hosil qiling.
• Karton klinometrning mustahkamligini ta'minlaydi.
2-qadam: Teshik hosil qiling.
• O'tkir buyumdan (masalan, qalam, igna yoki
qaychi) foydalanib, transportyor burchagiga yaqin
joydan ehtiyotkorlik bilan kichik teshik oching. Bu
teshik ipning o'tishiga imkon beradi va klinometr
ko'rsatkichi uchun o'q vazifasini bajaradi.

89.

Qiyalik o‘lchagich yarating (Clinometer)
3-qadam: Tayoqchachani mahkamlang.
• Trubkachani transpartyorning 90° li chizig‘i
bo‘ylab mahkam yopishtiring.
• Klinometr uchun tayoqcha ko'rish
vositasi sifatida ishlaydi.
• Tayoqcha tranpartyorning chetiga
to'g'ri kelishiga va yopishqoq lenta
bilan mahkam yopishtirilganligiga
ishonch hosil qiling
S
t
r
a
w

90.

Qiyalik o‘lchagich yarating (Clinometer)
4-qadam: Ip va sharchani qo'shing.
• Ipni transpartyor burchagi yonidagi kartonda qilingan teshikdan o'tkazing
• Ipning bir uchini plastilin sharga mahkam bog‘lang.
• Ipning ikkinchi uchi erkin osilib turishi va o‘tkazgich markaziga to‘g‘ri kelishi
uchun mahkamlanganligiga ishonch hosil qiling.
• Shar osilgan ip mayatnik vazifasini bajaradi va klinometr egilganida
transportyordagi ma’lum burchakka ishora qiladi.

91.

Qiyalik o‘lchagich (Clinometer) qanday ishlatiladi?
1. Balandligini o‘lchamoqchi bo‘lgan binongizdan taxminan 10 m dan 20 m
gacha bo‘lgan joyda turing. Masofani aniq o‘lchang.
2. Klinometrning trubkachasi orqali binoning yuqori qismiga qarang.
Sherigingizdandan klinometringizdagi ko‘tarilish burchagini so'rang
3. Binoning balandligini aniqlash uchun trigonometrik nisbatlardan
foydalaning. Ishingizni aniq ko'rsating. Klinometrning yerdan ma’lum
balandlikda ekanligini unutmang

92.

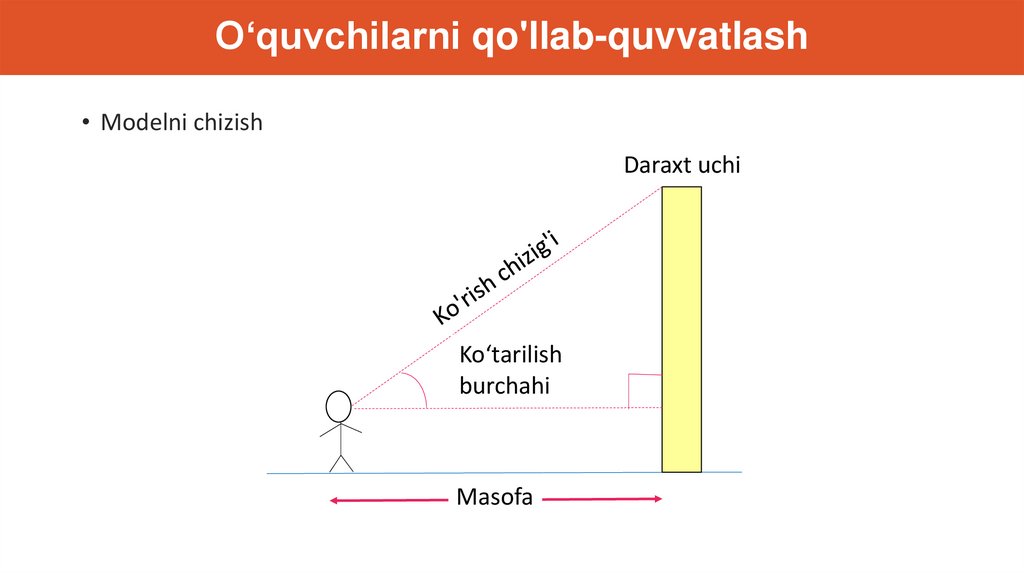
O‘quvchilarni qo'llab-quvvatlash
• Modelni chizish
Daraxt uchi
Ko‘tarilish
burchahi
Masofa

93.

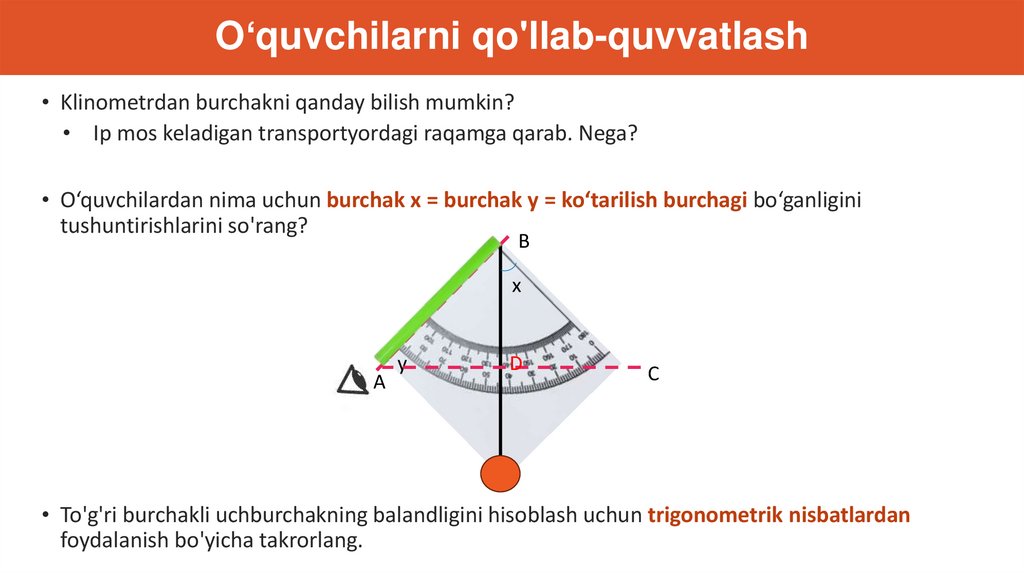
O‘quvchilarni qo'llab-quvvatlash
• Klinometrdan burchakni qanday bilish mumkin?
• Ip mos keladigan transportyordagi raqamga qarab. Nega?
• O‘quvchilardan nima uchun burchak x = burchak y = ko‘tarilish burchagi bo‘ganligini
tushuntirishlarini so'rang?
B
x
A
y
D
C
• To'g'ri burchakli uchburchakning balandligini hisoblash uchun trigonometrik nisbatlardan
foydalanish bo'yicha takrorlang.

94.

O‘quvchilarni qo'llab-quvvatlash
• To'g'ri burchakli uchburchakning balandligini hisoblash uchun
trigonometrik nisbatlardan foydalanishni takrorlang.
• Odatiy xato - Yerdan ko'z darajasigacha bo'lgan balandlikni hisobga
olmaslik.

95.

Tanaffus
Source: Used with permission – Microsoft Stoc

96.

3-Mashg‘ulot
Source: Used with permission – Microsoft Stoc

97.

Brahma afsonasi
Qadimgi hind afsonasida aytilishicha, Brahma Benaresdagi ibodatxonaga 64 ta
oltin disk qo'ygan va uni Brahma minorasi deb atagan. Ruhoniylarga disklarni bir
qoziqdan ikkinchisiga o'tkazish uchun uzluksiz ishlash kerakligi aytilgan.
Qoidalar:
1. Bir vaqtning o‘zida faqat bitta diskni
ko‘chirish mumkin.
2. Kattaroq diskni kichikroq diskka qo‘yib
bo‘lmaydi .
3. Barcha disklar tartibini saqlab, uchinchi
tayoqchaqa ko‘chirilishi kerak
Afsonada aytilishicha, oxirgi harakat qilinganda dunyo yo‘q bo'lib ketadi! Biz
shunda qancha yashashimiz kerak? Keling, hisoblaylik!

98.

Xanoy minorasi - 3 ta disk
Maqsad:
• Barcha 3 ta diskni eng kam harakat bilan birinchi
qoziqdan uchinchi qoziqqa o‘tkazish kerak.
Qoidalar:
1. Bir vaqtning o‘zida faqat bitta diskni ko‘chirish
mumkin.
2. Kattaroq diskni kichikroq diskka qo‘yib bo'lmaydi .
3. Barcha disklar tartibini saqlab, uchinchi tayoqchaqa
ko‘chirilishi kerak
Eng kam harakatlar soni qancha?

99.

Xanoy minorasi - Disklar sonining ko'payishi bilan
• Endi 4 ta disk bilan sinab ko'raylik. Eng kam harakatlar soni qancha?
• Endi 5 ta disk bilan sinab ko'raylik. Eng kam harakatlar soni qancha?
• Ketma-ketlik bormi?
Umuman olganda, n ta ob'ekt uchun 2n – 1 ta harakat kerak

100.

Brahma afsonasi
Afsonada aytilishicha, oxirgi harakat qilinganda dunyo yo'q bo'lib ketadi! Biz
shunda qancha yashashimiz kerak? Keling, hisoblaylik!
Barcha 64 ta oltin diskni uzatish uchun
minimal harakatlar soni qancha
264 – 1 = 18, 446, 744, 073, 709, 551, 615
= 1.85 × 1019
Dunyo halokatdan xavfsizdek tuyulyapdi!
.

101.

Xanoy minorasi - kontseptual tushunish va Amaliy
ko'nikma
4-modul (M4): Kontseptual tushuncha
• Shakllar va munosabatlarni aniqlash orqali algebraik fikrlashni
rivojlantirish.
• Moddiy-Rasmliy-Timsolli (M-R-T) yondashuviga mos keladi.
5-modul (M5): Amaliy ko‘nikma
• Bosqichma-bosqich algoritmik fikrlashni shakllantiradi.
• Yo‘naltirilgan amaliyot va takrorlash orqali o‘zlashtirishni
mustahkamlaydi.

102.

Kontseptual
tushunish
(takrorlash)
Source: Used with permission – Microsoft Stoc

103.

Kontseptual tushuncha
• Van De Vall, Karp, va Bay-Uilliams (2010) fikriga ko‘ra, tushunish "g'oyaning
mavjud g'oyalar bilan bog'lanish sifatining o'lchovi" kabi ta'riflanadi (23bet).
• Kontseptual tushunish - bu "munosabatlar yoki mavzuning asosiy g‘oyalari
haqidagi bilim".
• Agar o‘quvchi tushunchaning barcha kichik konstruksiyalarini (g‘oyalarini)
tushunsa va bu kichik konstruksiyalar orasidagi bog‘liklikni anglasa, shunda
o‘quvchi kontseptual tushunchaga ega bo‘lgan bo‘ladi.

104.

Richard Skempning matematikani tushunishi haqida
Richard Skemp (1976) matematikada
tushunishning ikki turini kiritdi:
Amaliyotda tushunish: nima uchun ishlashini
tushunmasdan, to'g'ri javob olish uchun
qoidalar va protseduralarni (bosqichlarni)
qanday qo'llashni bilish.
Munosabatlarni tushunish: Matematik
protseduralar va tushunchalar orqasidagi
bog‘liqliklarni nafaqat qanday, balki nima uchun
ekanligini ham tushunish.
Richard Skemp

105.

Richard Skemp – Amaliyotda tushunish
Ta'rif:
Amaliyotda (instrumental) tushunish to'g'ri javob olishga qaratilgan
muammolarni hal qilish uchun zarur bo'lgan matematik qoidalar va
protseduralarni (bosqichlarni) bilishni anglatadi.
Xususiyatlari:
Qoidalarni eslab qolishga e'tibor berish.
Asosiy tushunchalarni tushunishning ahamiyati yo'q.
Ko'pincha tushunmasdan faqatgina "qoidaga rioya qilish" ga sabab bo‘ladi.

106.

Richard Skemp – Munosabatlarni tushunish
Ta'rif:
Munosabatlarni tushunish matematikaning protsessual va kontseptual
jihatlarini tushunishni, metod nima uchun ishlashini va uning kengroq
matematik g'oyalar bilan qanday bog'lanishini bilishni o'z ichiga oladi.
Xususiyatlari:
Matematik tushunchalarning o'zaro bog'liqligini ta'kidlaydi.
Notanish kontekstlarda muammolarni hal qilishni qo'llab-quvvatlaydigan
chuqur, kontseptual tushunishni rag'batlantiradi.
Fikrlashni moslashuvchan qiladi va matematik bilimlarni uzoq muddatli
saqlash uchun asos yaratadi.

107.

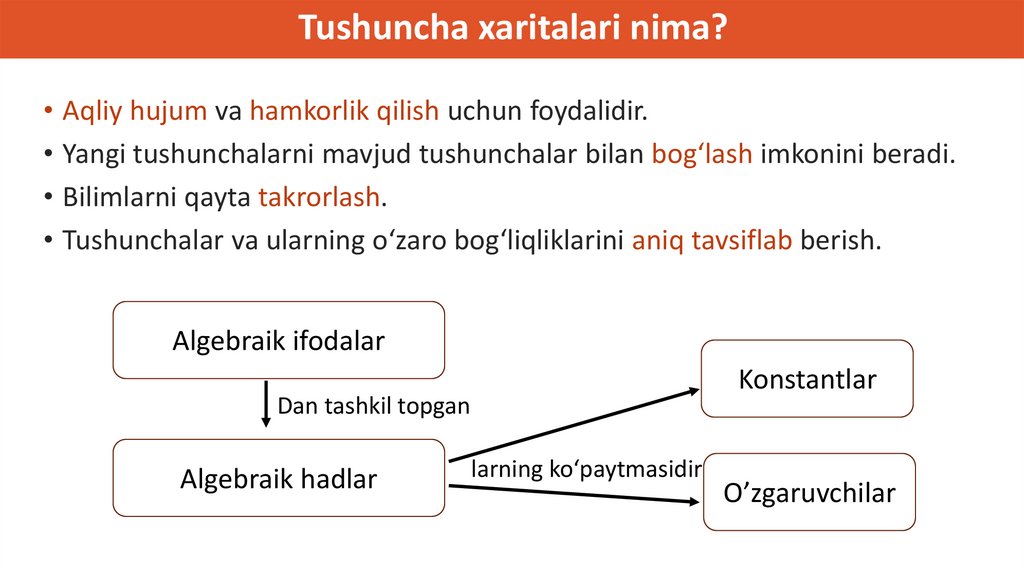
Kontseptual bilim
Hibert va Lefevrning tushuntirishi (1986):
Kontseptual bilim eng aniq munosabatlarga boy bilim sifatida tavsiflanadi.
Uni bir-biriga bog'langan bilimlar tarmog'i, bog'lovchi aloqalar
ma'lumotlarning alohida qismlari kabi muhim bo'lgan tarmoq sifatida ko'rish
mumkin.
Aloqalar individual faktlar va takliflarni qamrab oladi, shuning uchun barcha
ma'lumotlar ba'zi bir tarmoqqa bog'lanadi. (3-4-betlar)

108.

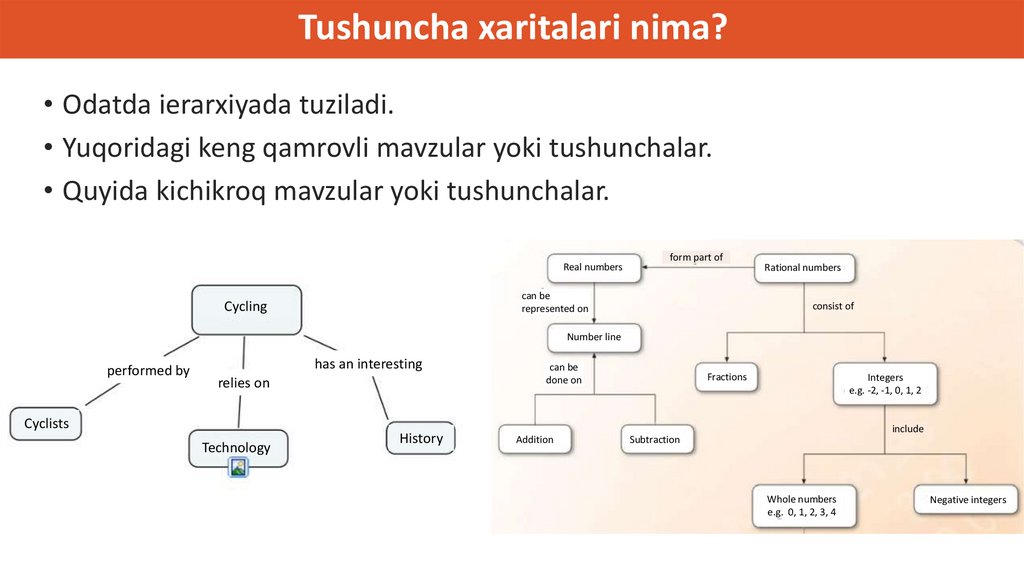
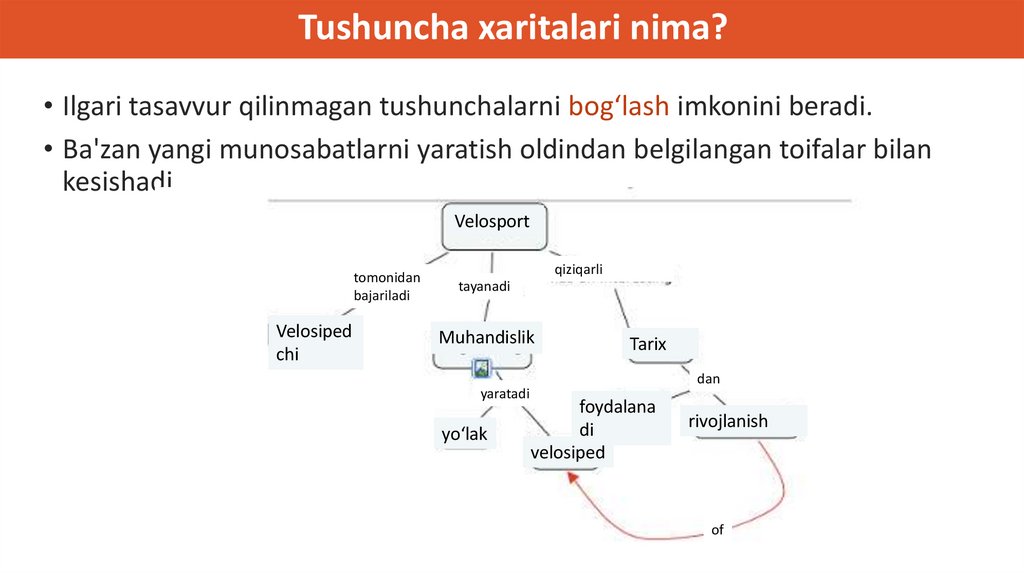
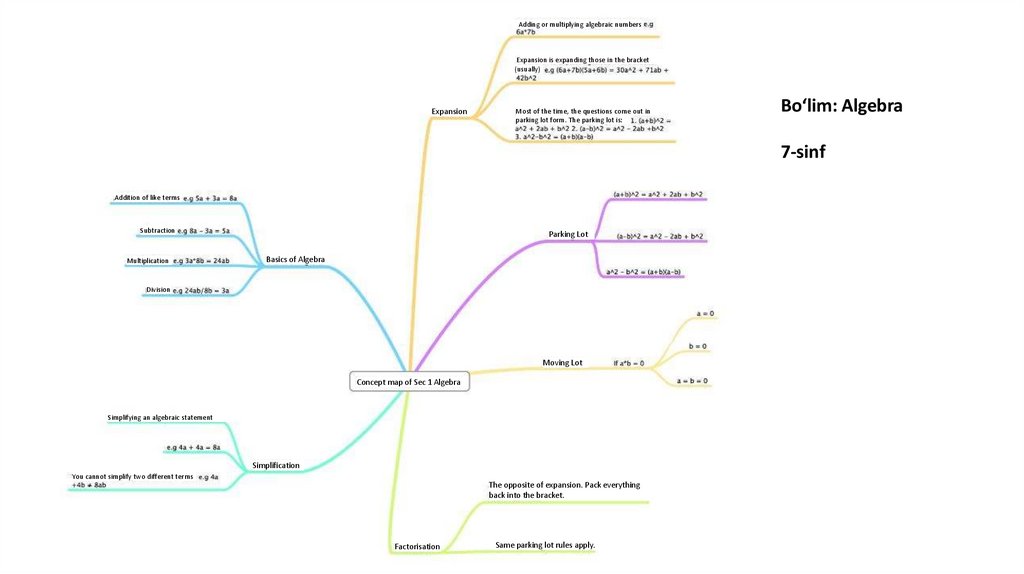
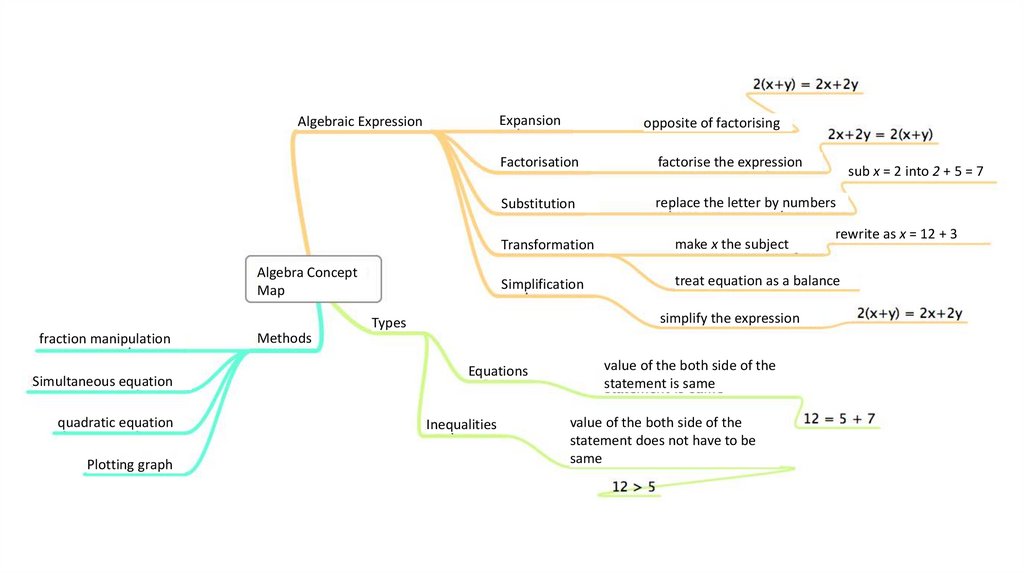
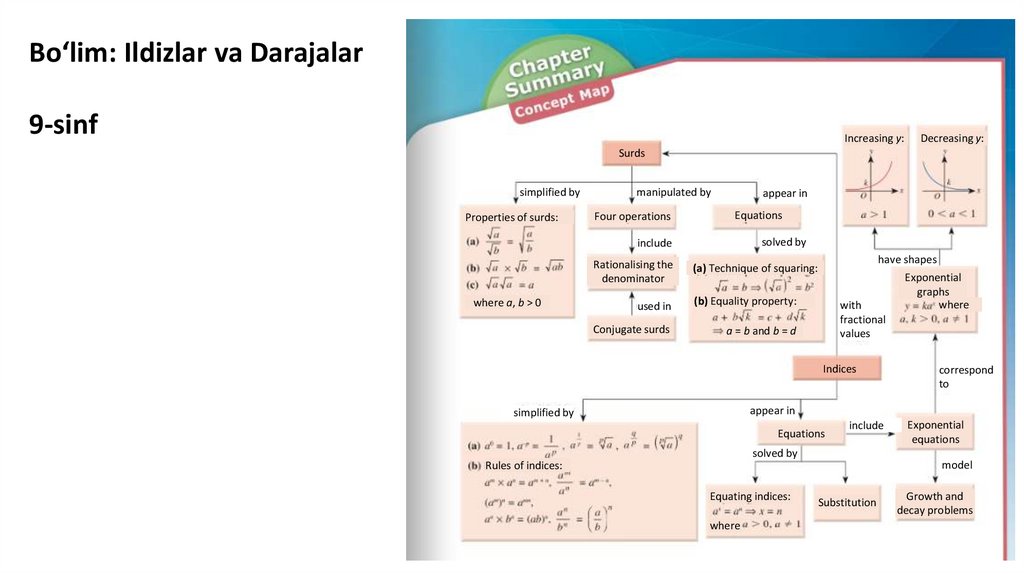
Kontseptual aloqalarni rivojlantirish
• Darslarda yoki darsliklarda tushunchalar o'rtasidagi bog'liqlik kamdankam uchraydi.
• Talabalarga kontseptual aloqalarni turli xil grafik vositalar yordamida
yetkazish mumkin:
Tushunchalar xaritasi
Venn diagrammasi
Daraxt diagrammasi
Kerol diagrammasi
Kontseptsiya xaritasi

109.

1. Venn
Diagrammasi

110.

Venn Diagram
• Ushbu mavzu o'quvchilarga to'plamlar to'g'risida qism to'plam
munosabatlarini ko'rsatish bilan o'rgatiladi: Agar A ning har bir elementi B
to‘plamda ham bo'lsa. A to'plam B to'plamining qism to'plamidir,
• Ravshanki, B to'plam kattaroq to'plamdir va bu g'oya Venn
diagrammalaridan kontseptual munosabatlarni tasvirlash uchun
foydalanilganda oson qo'llaniladi.

111.

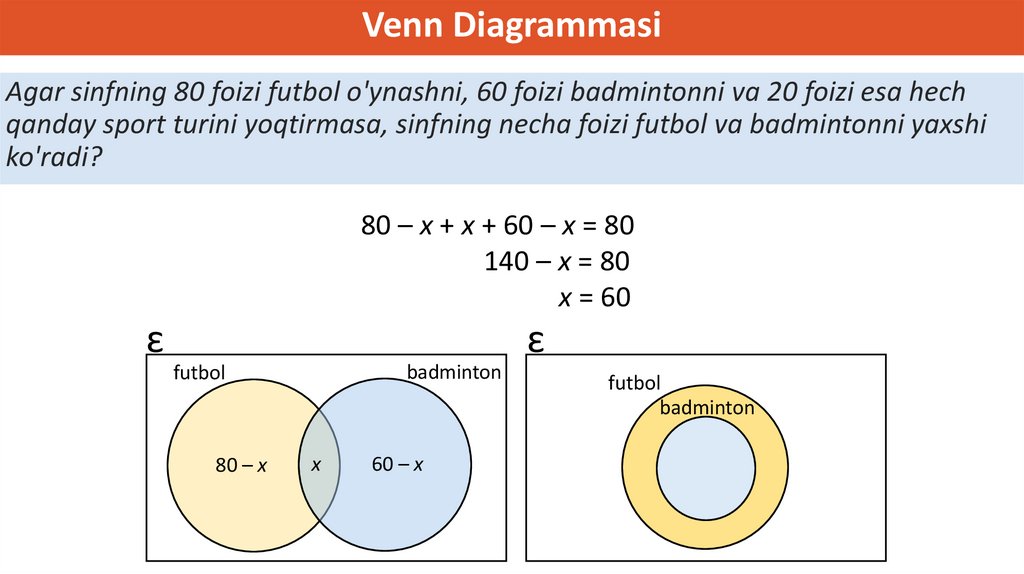
Venn Diagrammasi
Agar sinfning 80 foizi futbol o'ynashni, 60 foizi badmintonni va 20 foizi esa hech
qanday sport turini yoqtirmasa, sinfning necha foizi futbol va badmintonni yaxshi
ko'radi?
80 – x + x + 60 – x = 80
140 – x = 80
x = 60
ɛ
badminton
futbol
80 – x
x
60 – x
ɛ
futbol
badminton

112.

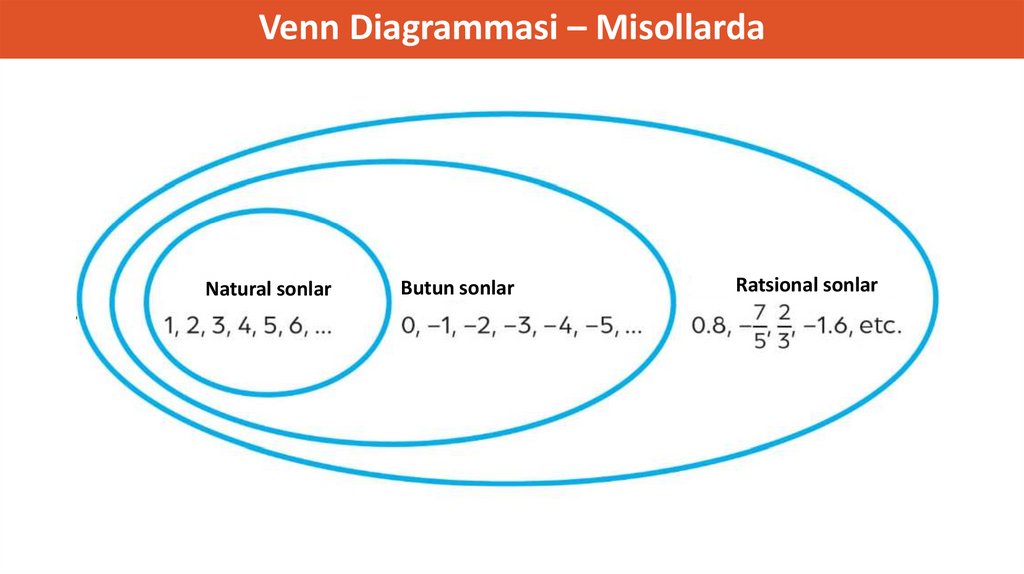
Venn Diagrammasi – Misollarda
Natural sonlar
Butun sonlar
Ratsional sonlar

113.

4-Mashg‘ulot
Source: Used with permission – Microsoft Stoc

114.

4-Mashg‘ulot – Venn Diagrammasi yaratish
Ushbu tushunchalar o'rtasidagi munosabatlarni ko'rsatish uchun Venn
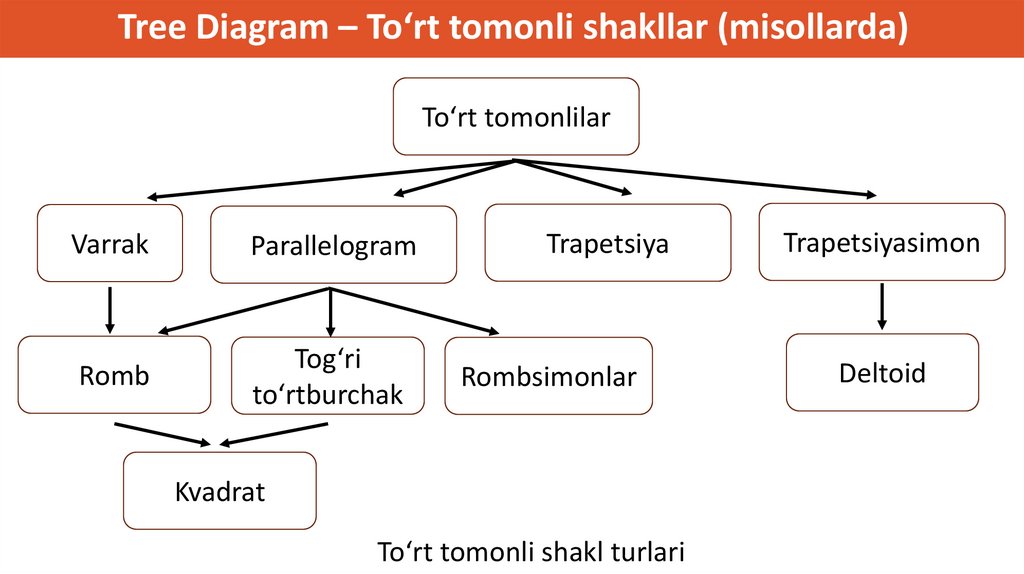
diagrammasini yarating:
Kvadrat, to'rtburchak, romb va parallelogramm (toq guruhlar uchun)
Natural sonlar, butun sonlar, ratsional, irratsional va haqiqiy sonlar (juft
guruhlar uchun)

115.

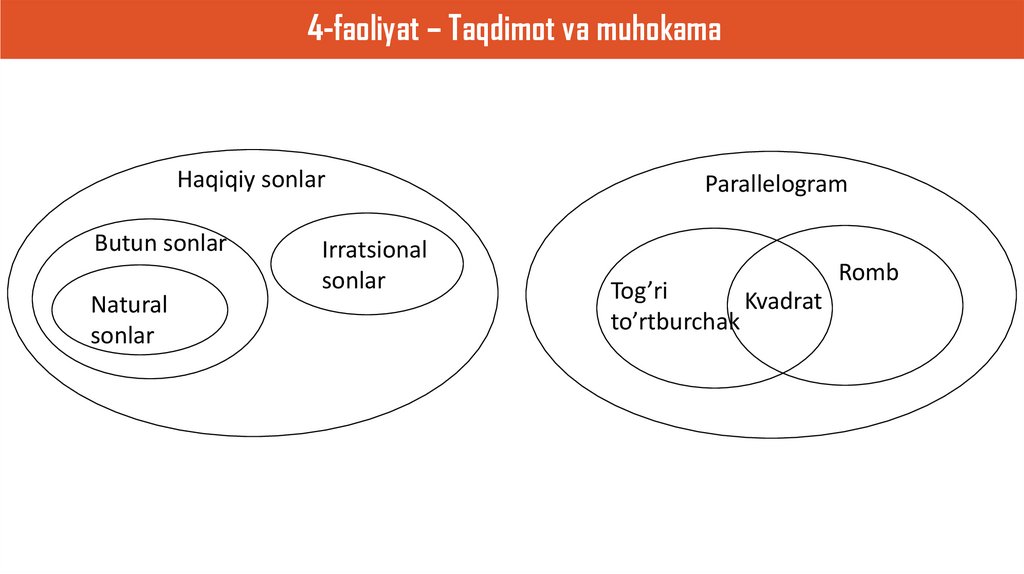
4-faoliyat – Taqdimot va muhokama
Haqiqiy sonlar
Butun sonlar
Natural
sonlar
Irratsional
sonlar
Parallelogram
Tog’ri
Kvadrat
to’rtburchak
Romb

116.

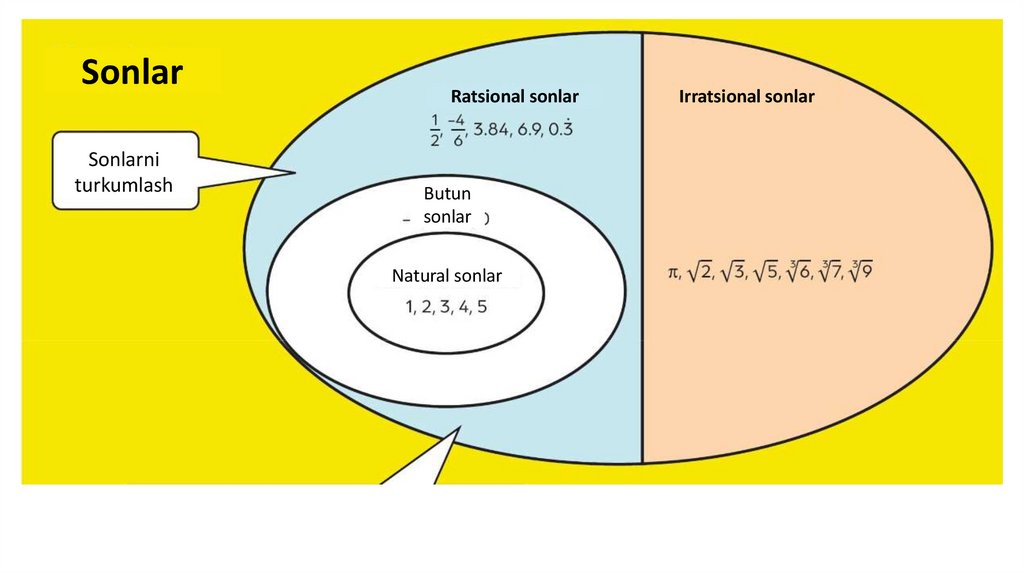
Sonlar
Sonlarni
turkumlash
Ratsional sonlar
Butun
sonlar
Natural sonlar
Irratsional sonlar

117.

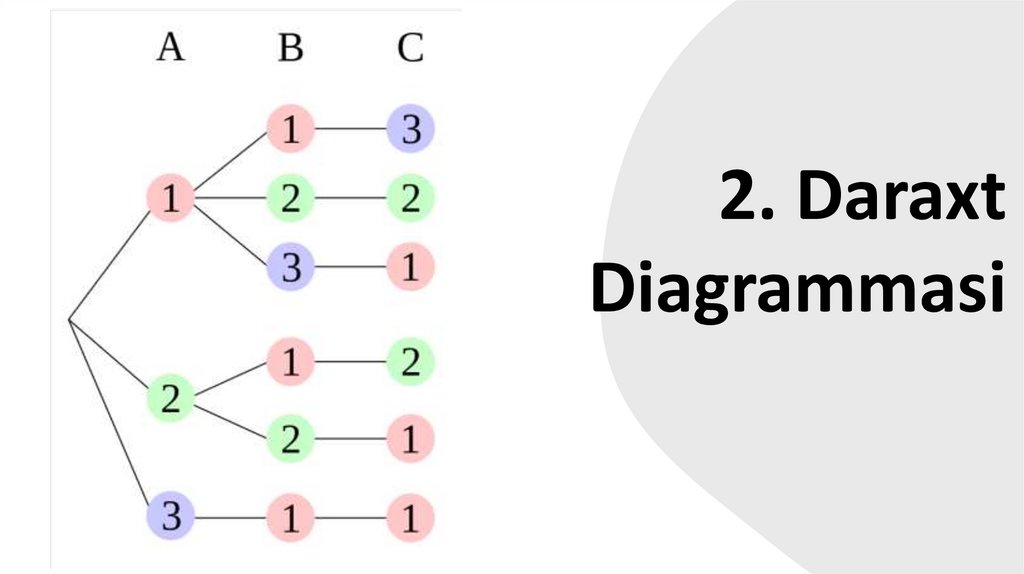
2. Daraxt
Diagrammasi

118.

Daraxt diagrammasi
Bir sumkada turli xil rangdagi 4 ta shar bor - qizil (Q), to'q sariq (T), sariq (S) va
yashil (Y). Ikkita to'p sumkadan tasodifiy ravishda, qayta joylanmasdan olinadi.
Qizil to'pni, keyin sariq to'pni chiqish ehtimolini toping.
1-olish
2-olish
Natijalar
Daraxt diagrammasidan ikkita to'pni qayta
joylanmasdan, sumkadan tasodifiy olinganda 12 ta
mumkin bo'lgan natijalar mavjud. Barcha 12 ta
natijaning yuzaga kelish ehtimolligi bir xil.
P (qizil, keyin sariq shar chiqishi) =