Amaliy ko'nikmalarni rivojlantirish

1.

Matematika fani
bo'yicha mastertrenerlar uchun malaka
oshirish treningi
Modul nomi: Amaliy ko'nikmalarni
rivojlantirish
© 2024 All rights reserved.

2.

6 – Dars

3.

Keling, eslab
olaylik!

4.

Quiz

5.

Qunt bilan
o'rganish
Qiziqish
Bilimlarni
qadrlash
O'ziga Ishonch
Fanga
munosabat
Qat'iyat
Hisoblashlarni bajara
olish
Algebraik shakl
almashtirishlar
Fazoviy tasavvur
Ma'lumotlarni tahlil qilish
O'lchash
Matematik uskunalardan
foydalanish
Baholash
O'z fikrlash (o'rganish)
jarayonini tahlil qilish
O'z organish jarayonini
tartibga solish
Mathematik
muammolarni
hal qilish
Tushuncha
lar
Sonli
tushunchalar
Algebraik
munosabatlar
Geometrik
tushunchalar
Statistik tahlil
Ehtimollik
Mulohaza yuritish, muloqot va
munosabatlar
Modellashtirish va tadbiq etish
Fikrlash qobiliyatlari va
evristika

6.

_________________, yoki fikrlash (o'rganish) jarayonini
tahlil qilish, insonning o'z fikrlash qobiliyatini anglash va
o'rganish jarayonini tartibga solish.
• Savollar o'zbek tiliga tarjima qilingan va men
Kahoot-ga ko'chirib, keyin uni slaydlarga
joylashtirganman. Demak sizlarga Kahoot havolasi
1.oldindan
Tushunchalar
beriladi va ushbu havola orqali savollarga
berishingiz mumkin bo'ladi.
2.javob
Qobiliyatlar
(Ko'nikmalar)
3. Jarayonlar
4. Metakognitiv
anglash
5. Qadriyatlar
(Munosabatlar)

7.

Singapur matematika o'quv dasturi doirasida qaysi komponenti ya’ni
tarkibiy qism (asos) laridan biri, o'quvchilarni fikrlash
jarayonlarini aks ettirish uchun ularning mustaqil jurnal yuritish
faoliyatiga jalb qilinishi muhim deb ta’kidlaydi?
1. Tushunchalar
2. Qobiliyatlar
(Ko'nikmalar)
3. Jarayonlar
4. Metakognitiv
anglash
5. Qadriyatlar
(Munosabatlar)

8.

O'quvchilarga o'z o'quv jarayonini faol
boshqarishga qanday yordam bera olamiz?
1. Ko'proq amaliy misollar berish.
2. Ko'proq uyga vazifa topshiriqlari berish.
3. Bob yoki bo'lim oxirida o'z-o'zini baholash
nazorat topshiriqlar bilan doimiy ta’minlash.
4. Matematik qo'shiq kuylash.

9.

Singapur matematika o'quv dasturi doirasida qaysi komponenti ya’ni
tarkibiy qism (asos) laridan biri, o'ziga ishonch, qiziqish va
fanga munosabat, qat'iyatlilik kabi matematikaga ijobiy munosabatni
rivojlantirishga qaratilgan?
1. Tushunchalar
2. Qobiliyatlar
(Ko'nikmalar)
3. Jarayonlar
4. Metakognitiv
anglash
5. Qadriyatlar
(Munosabatlar)

10.

O'quvchilarning o'z fikrlashlarini mustaqil
rivojlantirishlari uchun ularga qanday imkoniyat
yoki yordam bera olamiz?
1. Ko'proq matematik muammoli masalalarni berish.
2. O'quvchilarni Polyaning muammolarni hal qilish
usulidan foydalanishga jalb qilish.
3. O'quvchilarni Polyaning muammolarni hal qilish
usulidan foydalanishga jalb qilish.

11.

Bugungi darsning maqsadlari:
• O'quvchilar uchun mazmunli o'rganish, amaliy
ko'nikmalarni rivojlantirish va quyidagi
tajribalarga asoslanib amalga oshirish:
o Singapur matematika o'quv dasturining
tamoyillariga murojat qilish
o Tushunchalar, ko'nikmalar, jarayonlar,
munosabatlar va metakognitiv anglashni
o'zaro integratsiyalash
• Matematikani o'rganishda muammoni chuqur
tushunish va uni samarali hal qilish qobiliyatini
rivojlantirish
Source: Used with permission – Microsoft Stock Image

12.

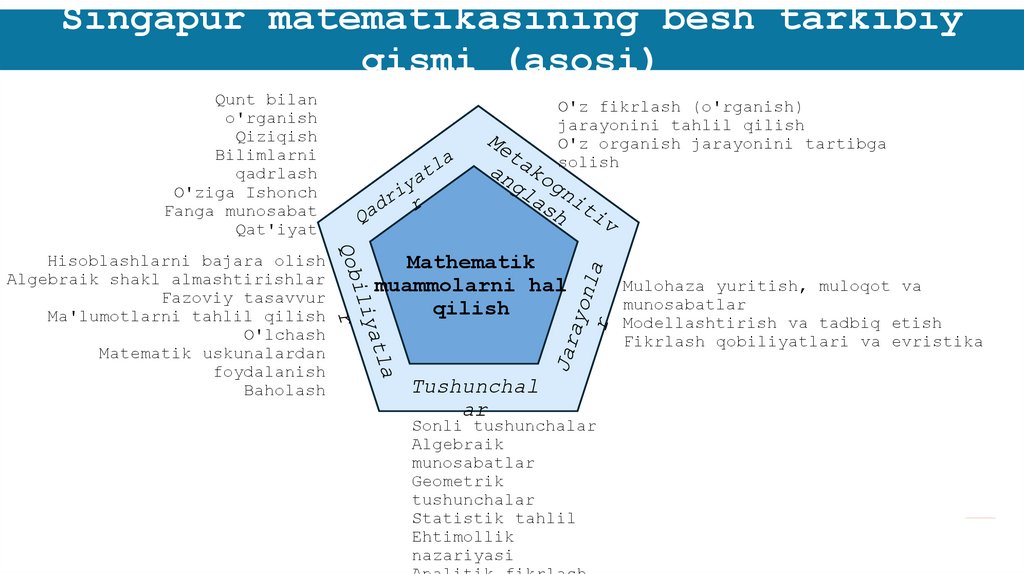
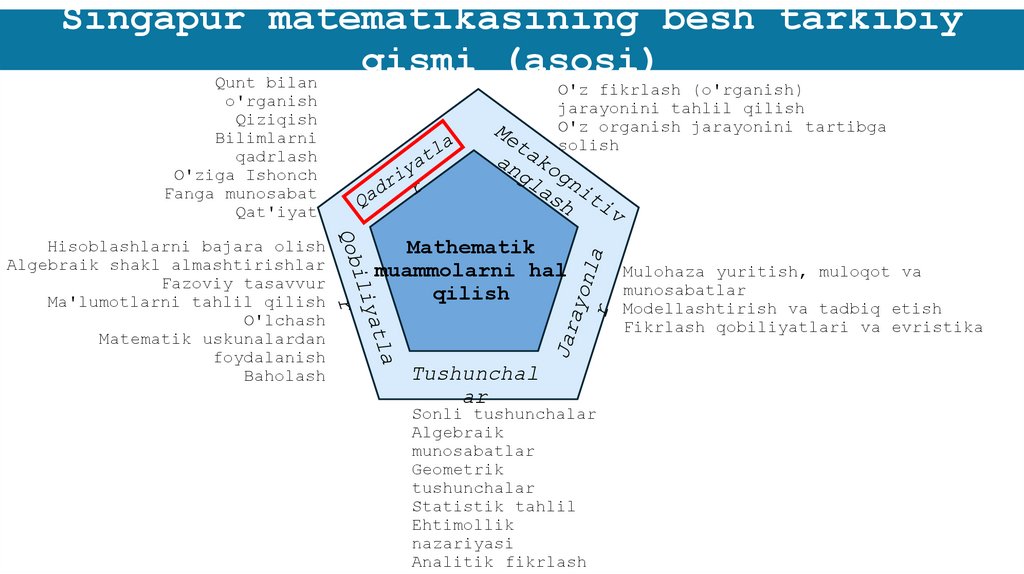
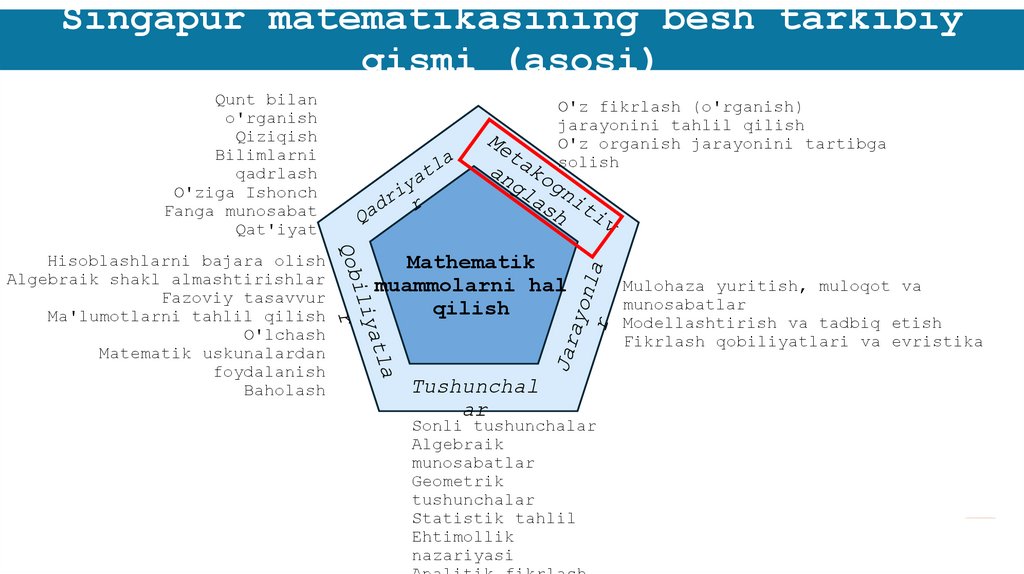
Singapur matematikasining besh tarkibiy
qismi (asosi)
Qunt bilan
o'rganish
Qiziqish
Bilimlarni
qadrlash
O'ziga Ishonch
Fanga munosabat
Qat'iyat
Hisoblashlarni bajara olish
Algebraik shakl almashtirishlar
Fazoviy tasavvur
Ma'lumotlarni tahlil qilish
O'lchash
Matematik uskunalardan
foydalanish
Baholash
O'z fikrlash (o'rganish)
jarayonini tahlil qilish
O'z organish jarayonini tartibga
solish
Mathematik
muammolarni hal
qilish
Tushunchal
ar
Sonli tushunchalar
Algebraik
munosabatlar
Geometrik
tushunchalar
Statistik tahlil
Ehtimollik
nazariyasi
Mulohaza yuritish, muloqot va
munosabatlar
Modellashtirish va tadbiq etish
Fikrlash qobiliyatlari va evristika

13.

O'quv dasturini tarkibiy qismlari
O'quv dasturida yoritilgan tushunchalar va ko'nikmalar 3 ta mazmun sohasi
bo'yicha tuzilgan. Jarayonlarning rivojlanishi, metakognitiv anglash va
munosabatlar mazmuni bilan bog'liq bo'lgan o'quv tajribalariga ajratiladi
Bilim va ko'nikmalar
Son tushunchasi va Algebra
Geometriya va o'lchashlar
Statistika va Ehtimollik
O'rganish ko'nikmalari (tajribalari)
(jarayonlar, metakognitiv anglash va munosabatlar)

14.

Amaliy
ko'nikmalarni
rivojlantirish–
Nima uchun &
Qanday qilib ?

15.

Amaliy ko'nikmalarni rivojlantirish– Nima uchun?
• Matematikani o'rganish shunchaki tushunchalar va ko'nikmalarni
o'rganish emas.
• O'rganishni anglash va metakognitiv bilish qobiliyatlar bir xil
darajada muhimdir.
• Ta'lim tajribalari o'quvchilarning XXI asr rivojlanish yutuqlariga
hissa qo'shuvchi omil bo'lib, biz bu natijaga matematikani samarali
o'qitish va o'rganish orqali erishmoqchimiz.

16.

Amaliy ko'nikmalarni rivojlantirish – Nima uchun?
• O'quvchilarni izlanuvchanlikka undash.
o O'qituvchilar o'quvchilarga matematik natijalarni mustaqil ravishda kashf qilishlari
uchun imkoniyatlar berishlari lozim.
• O'quvchilarda guruhlarda ishlash, guruh a’zolari fikrlarini hurmat qilish va muloqot qilish
qobiliyatlarini rivojlantirishga yordam berish.
o O'qituvchilar o'quvchilarga, muammo ustida birgalikda guruhda ishlash va tegishli
matematik yondashuv va usullardan foydalangan holda o'z g'oyalarini taqdim etish
imkoniyatini berishlari kerak.
• O'z-o'zini boshqarish va mustaqil o'rganish odatlarini rivojlantirish.
o O'qituvchilar o'quvchilarga o'quv maqsadlarini qo'yish va ular ustida maqsadli ishlash
imkoniyatini berishlari kerak.
Sinf xonalarida bunday imkoniyatlarga ega bo'lish, o'quvchilariga, XXI
asr rivojlantirish yangiliklarini kashf qilishlari uchun zamin yaratadi.

17.

Amaliy ko'nikmalarni rivojlantirish – Qanday qilib?
• O'quv jarayonida amaliy ko'nikmalarni rivojlantirish o'qituvchilarning dars
berish usullari hamda o'quvchilarning bilim olish jarayoniga ijobiy ta'sir
ko'rsatadi. Shu sababli, o'quv rejasida belgilangan maqsadlarga erishish uchun
matematika faniga oid o'quv dasturlari batafsil ishlab chiqilgan.
• “O'quvchilar ... imkoniyatiga ega bo'lishlari kerak" shaklida ifodalangan bu
bayonotlar o'qituvchilarga ushbu tajribalarning o'quvchi-markazda ekanligiga
qaratilganligini eslatadi.
• Ular o'qituvchilar tomonidan beriladigan ko'rsatmalar, imkoniyatlar va yo'lyo'riqlar bilan o'quvchilar bajaradigan turli mashg'ulotlar va ular namoyish qila
oladigan natijalarni tasvirlaydi.
• Ko'rsatmalar o'qituvchilarga nafaqat yo'l-yo'riq berishlariga yetarlicha aniq,
balki o'qituvchilarga moslashuvchanlikni ta'minlay olishlari uchun ham ular
ifodalay olishlari uchun qulay bo’lishi lozim.

18.

Amaliy Ko'nikmalarni Rivojlantirish (AKR)
O'quv jarayonida amaliy ko'nikmalarni rivojlantirish uchun ham aniqroq qilish
uchun:
• Har bir AKR ni o’rganishda quyidagi keltirilgan asoslarning kamida bittasi bilan
belgilanadi.
Asosiy maqsadlarni ko'rsatish uchun masalan: Jarayonlar (J), Metakognitiv
anglash (M) yoki Munosabatlar (M) va hokazo...
• O'quvchilar bajarishi kerak bo'lgan harakatlarni tavsiflovchi fe'llar har bir AKR
bayonoti uchun ajratib ko'rsatilgan harflar bilan ta'kidlangan.

19.

Kvadrat
funksiyalar
mavzusi misolida
o'rgatish va
o'rganishni
muhokama qilish

20.

Singapurda matematika ta'limining umumiy maqsadlari
1. Barcha o'quvchilarning matematika
bo'yicha o'zlashtirish va ega bo'lgan
bilimlarini, kundalik hayotda samarali
qo'llay olish darajasiga erishishlarini
ta'minlash.
2. Qiziqish va qobiliyatga ega bo'lgan
o'quvchilar uchun matematika bo'yicha
chuqur bilimga ega bo'lishlari va ular
ta'limning keyingi bosqichida murakkab
matematika masalalarini yechish uchun
tegishli kurslarni davom ettirishlariga
imkoniyat yaratish. (Qo'shimcha
matematika)

21.

O'quv dasturini tarkibiy qismlari
O'quv dasturida yoritilgan tushunchalar va ko'nikmalar 3 ta mazmun sohasi
bo'yicha tuzilgan. Jarayonlarning rivojlanishi, metakognitiv anglash va
munosabatlar mazmuni bilan bog'liq bo'lgan o'quv tajribalariga ajratiladi
Bilim va ko'nikmalar
Son tushunchasi va Algebra
Geometriya va o'lchashlar
Statistika va Ehtimollik
O'rganish ko'nikmalari (tajribalari)
(jarayonlar, metakognitiv anglash va munosabatlar)

22.

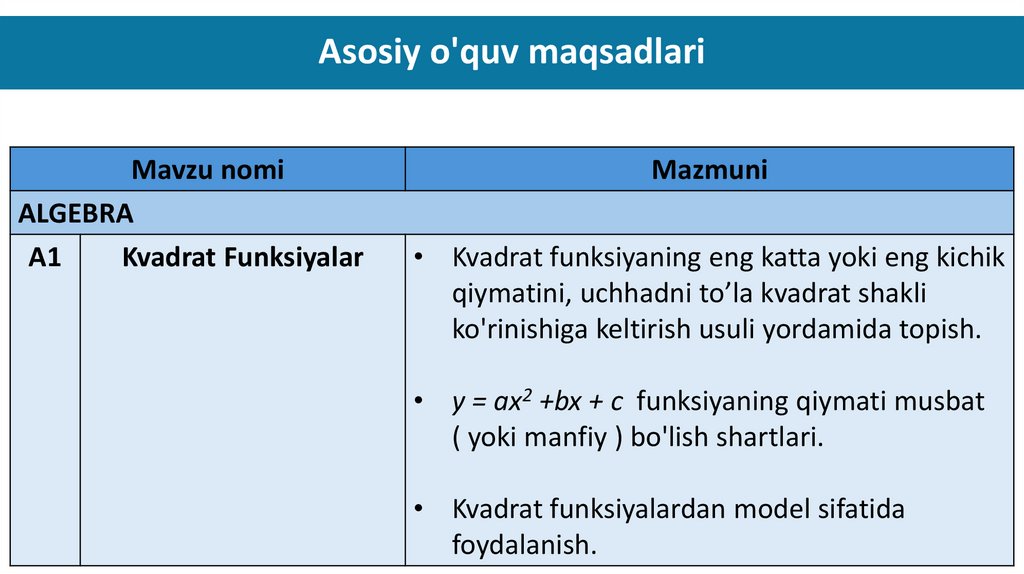
Asosiy o'quv maqsadlari
Mavzu nomi
ALGEBRA
A1
Kvadrat Funksiyalar
Mazmuni
• Kvadrat funksiyaning eng katta yoki eng kichik
qiymatini, uchhadni to’la kvadrat shakli
ko'rinishiga keltirish usuli yordamida topish.
• y = ax2 +bx + c funksiyaning qiymati musbat
( yoki manfiy ) bo'lish shartlari.
• Kvadrat funksiyalardan model sifatida
foydalanish.

23.

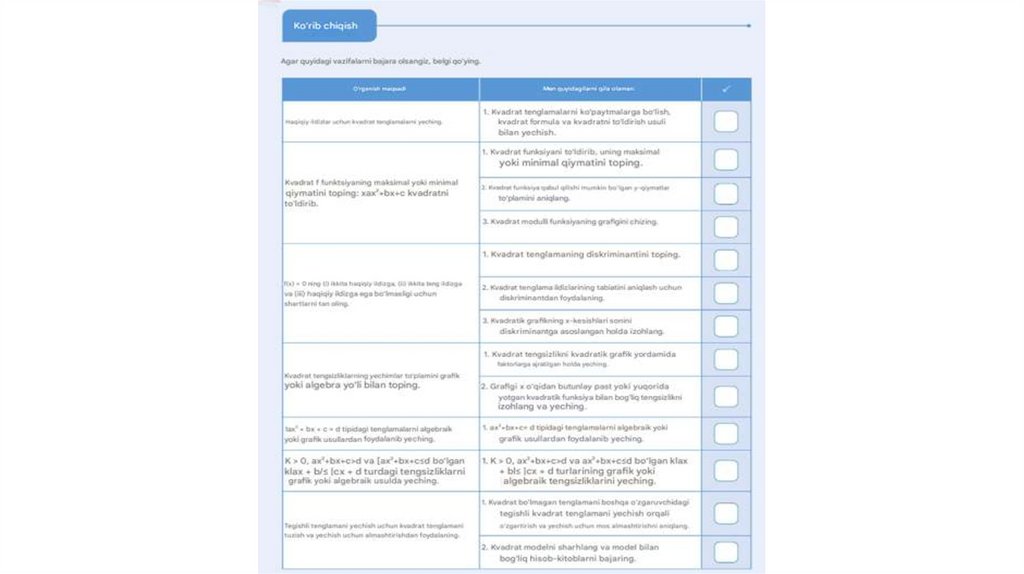
Oldindan talab qilinadigan ko'nikmalar (bilimlar).
• Kvadrat ifodani ko'paytuvchilarga ajratish a