Matematika fani bo‘yicha mastertrenerlar uchun malaka oshirish treningi

1.

Matematika fani
bo‘yicha mastertrenerlar uchun malaka
oshirish treningi
Modul nomi : Moddiy-Rasmli-Timsolli
yondashuv va hisoblashga oid ko‘rgazmali
qurollardan foydalanish orqali matematik
tushunchalarni anglash
© All rights reserved

2.

Bizning diqqatimizda
Qunt bilan
o‘rganish
Qiziqish
Bilimlarni
qadrlash
o‘ziga Ishonch
Fanga munosabat
Qat'iyat
Hisoblashlarni bajara olish
Algebraik shakl almashtirishlar
Fazoviy tasavvur
Ma'lumotlarni tahlil qilish
O‘lchash
Matematik uskunalardan
foydalanish
Baholash
O‘z fikrlash (o‘rganish)
jarayonini tahlil qilish
O‘qish jarayonida o‘z-o‘zini
tartibga solish
Mathematik
muammolarni hal
qilish
Tushunchal
ar
Sonli tushunchalar
Algebraik
munosabatlar
Geometrik
tushunchalar
Statistik tahlil
Ehtimollik
Mulohaza yuritish, muloqot va
munosabatlar
Modellashtirish va tadbiq etish
Fikrlash qobiliyatlari va evristika

3.

Ifodalash usulini o‘zgartirish
O‘quvchilarimga matematika fanini qanday o‘qitishim mumkin?
O‘quvchilarim matematika fanini qanday o‘rganishlari mumkin?
© All rights reserved

4.

4-modul: MODDIY-RASMLI-TIMSOLLI yondashuv va hisoblashga oid
ko’rgazmali qurollarda foydalanish orqali matematik tushunchalarni
tushunish
O‘quv maqsadlari:
O‘quvchilarning matematik tushunchalarni tushunishlarini yanada
mustahkamlash uchun 3 ta keng qirrali yondashuvni qabul qilish.
1. O‘quvchilarga matematik tushunchalarni o‘qitish va o‘rganish
ko‘nikmalarini rivojlantirish davomida MODDIY-RASMLI-TIMSOLLI
(MRT) yondashuvidan foydalanish.
2. O‘quvchilarga matematika tushunchalarini yaxshiroq va atroflicha
tushuntirish uchun Frayer modelidan foydalanish.
3. O‘quvchilarga turli matematik tushunchalarni Venn diagrammasi,
daraxtli diagramma va fikrlar xaritasi o‘rtasidagi bog‘liqliklarni
aniqlashlari uchun yo‘nalish berishda foydalanish.
© All rights reserved

5.

5-modul: Matematikaga oid ko‘nikmalarni rivojlantirish
O‘quv maqsadlari:
• O‘quvchilar uchun matematikaga oid ko‘nikmalarni
rivojlantirish uchun asosiy pedagogik yondashuvlar sifatida,
To‘g‘ridan-to‘g‘ri ko‘rsatmalar berib borish va o‘quvchilar
o‘zlari mustaqil matematik muammoni yechishlari uchun ularga
masuliyatni bosqichma-bosqich o‘tkazish yondashuvidan
foydalanish.
© All rights reserved

6.

Hamkorlikda ishlashdan kutilayotgan natijalarni belgilash
• Juftliklarda ishlash
• Muammoni yoningizdagi
sherigingiz bilan juftlikda yoki 3
kishi bo‘lib muhokama qiling
• Avval juftilikda- so’ng boshqalar
bilan fikr almashing
• Avval yoningizdagi sherigingiz
bilan juftlikda so’ng guruhingiz
boshqa a’zolari bilan fikr
almashing.
Source: Used with permission – Microsoft
Stock Image

7.

Bugungi trening darsning maqsadlari
Master trenerlarga trening davomida, qanday
qilib o‘z hududlaridagi oʻqituvchilarning
matematik tushunchalarni o‘quvchilarga
oʻqitishning turli yondashuvlaridan foydalanishni
tanishtirish. Bundan tashqari, o‘quvchilarning
samarali ta’lim olishlariga imkon berish zarur
ekanligini o‘rgatish.
O‘quvchilar matematik tushunchalarni chuqurroq
tushunishlari uchun Frayer modellaridan
foydalanish
Source: Used with permission – Microsoft Stock Image
Tushunchalarni ifodalashning turli usullaridan
foydalanish

8.

Matematika fani hamda
Matematikani o‘qitish va o‘rganish haqida qarashlar
• Sinfdagitajribalarimiz, ota-onalar va do'stlar bilan o‘zaro munosabatlarimiz
matematik hodisalarga bo'lgan e'tiqodimizni shakllantirishi mumkin.
• Bizning matematikaning mohiyatiga bo'lgan qarashlarimiz sinfdagi
amaliyotimizga sezilarli ta'sir ko'rsatishi haqida ko'plab dalillar mavjud
• Yangi o‘quv dasturlari yoki o‘quv dasturlarini isloh qilish harakatlarining
muvaffaqiyati, o‘qituvchilarning matematika hamda matematikani o‘qitish va
o‘rganishga bo‘lgan ishonchiga bog‘liq.
• O‘qituvchilar yangi o‘quv dasturlari yangiliklari yoki o‘zgarishlarini matematika
hamda matematikani o‘qitish va o‘rganish haqidagi mavjud munosabatlariga
moslashtira olsalar, ular yangi o‘quv dasturini muvaffaqiyatli amalga oshiradilar.
• Agar keng ko‘lamli farqlar yuzaga kelsa, o‘qituvchilar yangi o‘quv dasturini o‘z
qarashlariga moslashtirgan taqdirda ham, uni faqat qisman tatbiq etadilar yoki
deyarli amalda sinamaydilar
© All rights reserved
Source: Used with permission – Microsoft Stock

9.

Nature of
Mathematics
Matematikaning
mohiyati
© All rights reserved
Source: Used with permission – Microsoft Stoc

10.

Matematik qarashlar tizimi
Aniqlik bilan qarash
Matematik qarashlar
Matematika statik va o‘zgarmasdir.
Mustaqil mavjud bo‘lib, kashf qilinishni
kutmoqda.
Falibilist qarash
Matematika dinamik va rivojlanishda.
Ijtimoiy jihatdan qurilgan va o‘zgaruvchan
Matematik qarashlar tizimini tushunish bizga
• O‘z qarashlarimizz va ularning kelib chiqishi haqida mulohaza yuritishga
• Matematikada qarashlarning xilma-xilligini tan olishga
• O‘qitish va o‘rganishdagi natijalarini qadrlashga
yordam beradi
© All rights reserved

11.

Matematik qarashlarning 3 ta asosiy tashkil qiluvchilari
1. Matematikaning mohiyati haqida
tushuncha.
2. Matematika o‘qitish xususiyatining
modeli yoki ko‘rinishi.
3. Matematikani o‘rganish jarayonining
modeli yoki ko‘rinishi.
© All rights reserved
Source: Used with permission – Microsoft Stoc

12.

Pol Ernestning matematikani o‘rganishning 3 ta asosiy
tushunchasi
Matematikaga
1. Vosita sifatida qarash
1. Platonistik qarash
2. Muammolarni hal qiluvchi
sifatida qarash
© All rights reserved

13.

Matematikaning mohiyati: Matematika vosita sifatida
• Matematika foydali vosita sifatida.
• Faktlar, qoidalar va ko‘nikmalar
to‘plami.
• Foydalilik va dasturga e'tibor.
© All rights reserved
Source: Used with permission – Microsoft

14.

Vosita sifatida qarashda o‘qituvchining roli
• O‘qituvchilar ko‘rsatmalar beruvchi /
namoyish qiluvchi sifatida.
• To‘g‘ri tartiblar va usullarni o‘rgatishga
e'tibor qaratish.
• Amaliyot va takrorlashga ko‘proq
e'tibor qaratish.
© All rights reserved
Source: Used with permission – Microsoft

15.

Vosita sifatida qarashda o‘quvchilarning bilim olish jarayoni
• O‘zlashtirish va amaliyot orqali
o‘rganish.
• Qoidalar va tartiblarni eslab qolishga
e'tibor berish.
• Baholash to‘g‘ri qo‘llanilishiga
qaratilganlik.
© All rights reserved
Source: Used with permission – Microsoft

16.

Keling mulohaza qilamiz
Guruhda
• Ta’lim berish jarayoningiz haqida o‘ylab
ko‘ring.
• Yoshlikda matematikani asosan yodlash
va mashq qilish orqali o‘rgangan
vaqtingizni eslay olasizmi?
• Bu sizning mavzuni tushunish
va unga bo‘lgan
qiziqishingizga qanday
Source: Used with permission – Microsoft Stock Image

17.

Matematikaning mohiyati: Platonistik qarash
• Matematikani statik tushunish ,
birlashtirilgan bilimlar majmuasi
sifatida.
• Inson tafakkuridan tashqarida
mustaqil matematik
haqiqatlarning mavjudligi.
• Mantiqiy fikrlash va isbotlashga
urg‘u berish.
© All rights reserved

18.

Matematikaning mohiyati: Platonistik qarash
• Tub sonlarning xossalarini fanga
kiritish va ularni o‘rganish bu
qarashni namoyish qiladi.
• Misol. Nima uchun cheksiz ko‘p
tub sonlar mavjudligini tushunish
matematikada asosiy haqiqat
hisoblanadi?
© All rights reserved
Source: Used with permission – Microsoft
Stock Image

19.

Platonistik qarashda o‘qituvchining roli
• O‘qituvchi yo‘l
ko‘rsatuvchi/tushuntiruvchi
sifatida.
• O‘quvchilarning tushunchalar,
faktlar va haqiqatlarni
tushunishlariga yordam berish.
• Mantiqiy va tanqidiy fikrlashni
rag‘batlantirish.
© All rights reserved
Source: Used with permission – Microsoft
Stock Image

20.

Platonistik qarashda o‘quvchilarning bilim olish jarayoni
• Tushunish va sinchiklab
o‘rganish orqali bilimga ega
bo‘lish.
• Matematik tushunchalar,
qoidalar va tuzilmalar bilan
shug‘ullanish.
• Baholash fikrlash va isbotlashga
qaratilgan.
© All rights reserved
Source: Used with permission – Microsoft Stoc

21.

Matematikaning mohiyati: Muammolarni hal qiluvchi sifatida
qarash
• Matematika dinamik,
rivojlanayotgan soha sifatida.
• Inson faoliyati va ijtimoiy
jarayonlar orqali yaratilganlik
sifatida.
• So‘rovga qaratilganlik, taxmin
qilish va muammolarni hal
qilishga urg‘u berish asosida.
© All rights reserved
Source: Used with permission – Microsoft Stoc

22.

Matematikaning mohiyati: Muammolarni hal qiluvchi sifatida
qarash
• Fibonachchi sonlari ketma-ketligi kabi
qonuniyatlarni o‘rganish va uning
tabiatda qanday paydo bo‘lishini
o‘rganishni ko‘rib chiqing.
• Ushbu tadqiqot matematikaning
dinamik va ijodiy mohiyatini ko‘rsatadi.
© All rights reserved
Source: Used with permission – Microsoft
Stock Image

23.

Muammolarni hal qiluvchi sifatida qarashda o‘qituvchining roli
• O‘qituvchi fasilitator/murabbiy
sifatida.
• Izlanish va mustaqil fikrlashga
undovchi sifatida
• Birgalikda o‘rganish va muhokama
qilishni qo‘llab-quvvatlovchi sifatida.
© All rights reserved
Source: Used with permission – Microsoft Stoc

24.

Muammolarni hal qiluvchi sifatida qarashda o‘quvchilarning
bilim olish jarayoni
• Izlanuvchanlik va yaratuvchanlik
asosida o‘rganish.
• Muammoni hal qilish va izlanishlar
olib borishda faol ishtirok etish.
• Baholash jarayonlarini adolatli olib
borish va ijodkorlikka qaratilganlik.
© All rights reserved
Source: Used with permission – Microsoft
Stock Image

25.

Keling mulohaza qilamiz
• Agar o‘quvchilar biror
muammoning yechimini
topsalar, ular qanday qilib
mustaqil natijaga erisha
olishlari mumkinligi haqida
o‘ylab ko‘ring.
• Bu ularning matematika faniga
bo‘lgan aniqlik bilan yondashuvi
va qiziqishiga qanday ta'sir
qiladi?
© All rights reserved
Source: Used with permission – Microsoft Stoc

26.

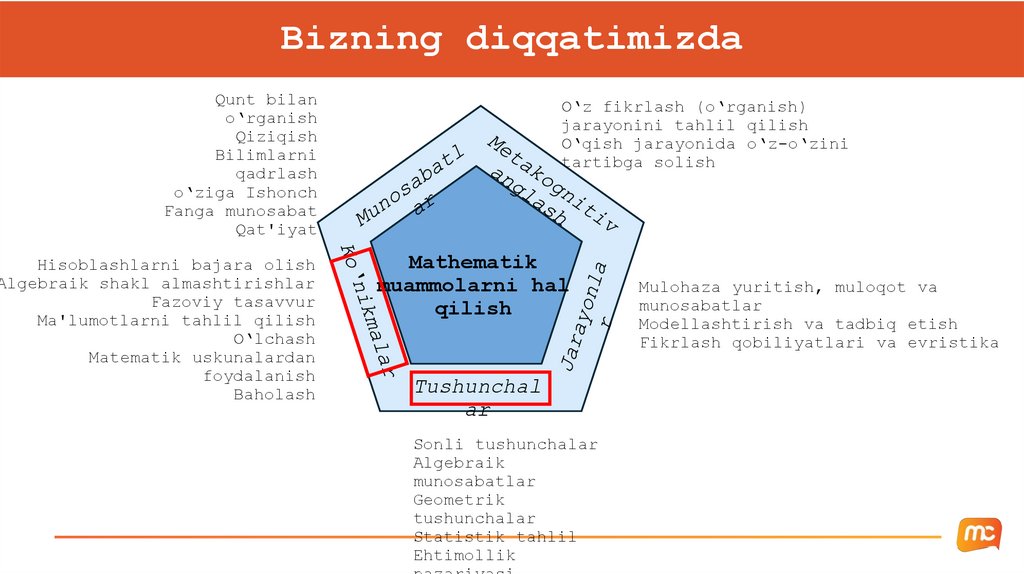
Matematikani o‘rganishning uchta asosiy jihatining qisqacha
mazmuni
Jihati
Vosita sifatida qarash
Platonistik qarash
Muammmolarni hal
qiluvchi sifatidal
Matematikaning
mohiyati
Amaliy foydalanish uchun
vosita
Belgilangan bilimlar
majmuasi
Dinamik, rivojlanib boruvchi
soha
O‘qituvchining roli
Ko‘rsatmalar beruvchi /
namoyish qiluvchi
Yo‘riqnoma
beruvchi/Izohlovchi
Yo‘naltiruvchi/Murabbiy
O'quvchining
o'rganishi
O'zlashtirish va amaliyot
Tushunish va mantiqiy
fikrlash
Tadqiqot va yaratish
© All rights reserved

27.

1 - mashg‘ulot
© All rights reserved
Source: Used with permission – Microsoft Stoc

28.

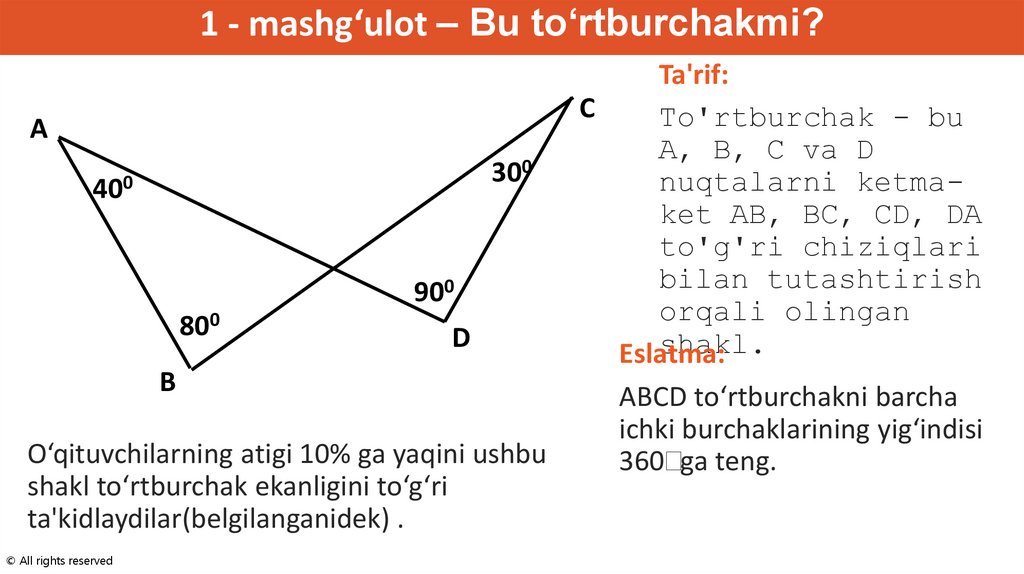
1 - mashg‘ulot – Bu to‘rtburchakmi?
A
300
400
900
800
D
B
O‘qituvchilarning atigi 10% ga yaqini ushbu
shakl to‘rtburchak ekanligini to‘g‘ri
ta'kidlaydilar(belgilanganidek) .
© All rights reserved
Ta'rif:
C
To'rtburchak - bu
A, B, C va D
nuqtalarni ketmaket AB, BC, CD, DA
to'g'ri chiziqlari
bilan tutashtirish
orqali olingan
shakl.
Eslatma:
ABCD to‘rtburchakni barcha
ichki burchaklarining yig‘indisi
360⸰ga teng.

29.

O‘qitish va o‘rganishning ta'siri
O‘qitish va o‘rganishda quyidagi ikkita
zaif jihat ko’zga tashlanadi:
1. Berilgan ta'riflar asosida to‘g‘ri xulosalar
chiqara olmaslik
2. Avval bilgan matematik ta’riflarning
alternativ variantlarini qabul qilmaslik.
Yuqori sinflarda matematikani o‘qitishda
ularni bartaraf etish kerak!
Source: Used with permission – Microsoft Stoc

30.

2 - mashg‘ulot
© All rights reserved

31.

2 - mashg‘ulot – Teng tomonli uchburchak ham teng
yonli uchburchakdir
• To‘g‘rimi yoki noto‘g‘rimi?
• To‘g‘ri (Yashil bayroq)
• Noto‘g‘ri (Qizil bayroq)
Javob: Bu vaziyatga qarab olinadi.
Ta'rif: Teng yonli uchburchak deb ikki tomoni teng bo‘lgan uchburchakka
aytiladi.
"Ikki" so‘zi nimani anglatadi?
• Tashqi ma'no – Evklid tomonidan takidlanishicha biz kundalik hayotda odatda
aynan ikkita deb ishlatamiz (Artmann, 1999).
• Ichki ma'no - kamida ikkita.
© All rights reserved

32.

Biz o‘quvchilardan quyidagi izohlarni so‘rashimiz
mumkinmi?
• Javob: Ha!
• O‘quvchilardan bunday bayonotlarni so‘rashdan maqsad,
ularning berilgan ta'rif asosida to‘g‘ri xulosa chiqarish
qobiliyatlarini baholashdir.
(Matematikada bu muammoni hal qilish asosida kechadi)
• O‘quvchilar o‘rtasida fikrlash va muloqot qila olishni
rivojlantiradi.
• Ba'zi o‘qituvchilar o‘z o‘quvchilaridan bu ta’riflarni har
doim ham to‘g‘ri deb eslab qolishlarini kutishadi.
• Bu holatda o‘qituvchilar matematik ta’riflarga qanday
qarashadi?
© All rights reserved
Source: Used with permission – Microsoft Stoc

33.

Tanaffus
Source: Used with permission – Microsoft Stoc

34.

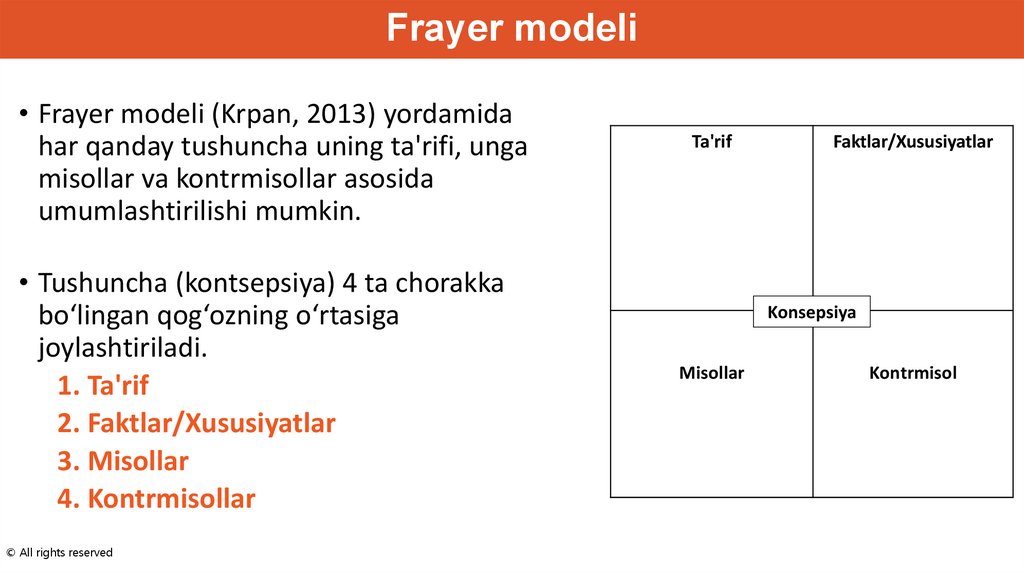
Frayer modeli
• Frayer modeli (Krpan, 2013) yordamida
har qanday tushuncha uning ta'rifi, unga
misollar va kontrmisollar asosida
umumlashtirilishi mumkin.
• Tushuncha (kontsepsiya) 4 ta chorakka
bo‘lingan qog‘ozning o‘rtasiga
joylashtiriladi.
1. Ta'rif
2. Faktlar/Xususiyatlar
3. Misollar
4. Kontrmisollar
© All rights reserved
Ta'rif
Faktlar/Xususiyatlar
Konsepsiya
Misollar
Kontrmisol

35.

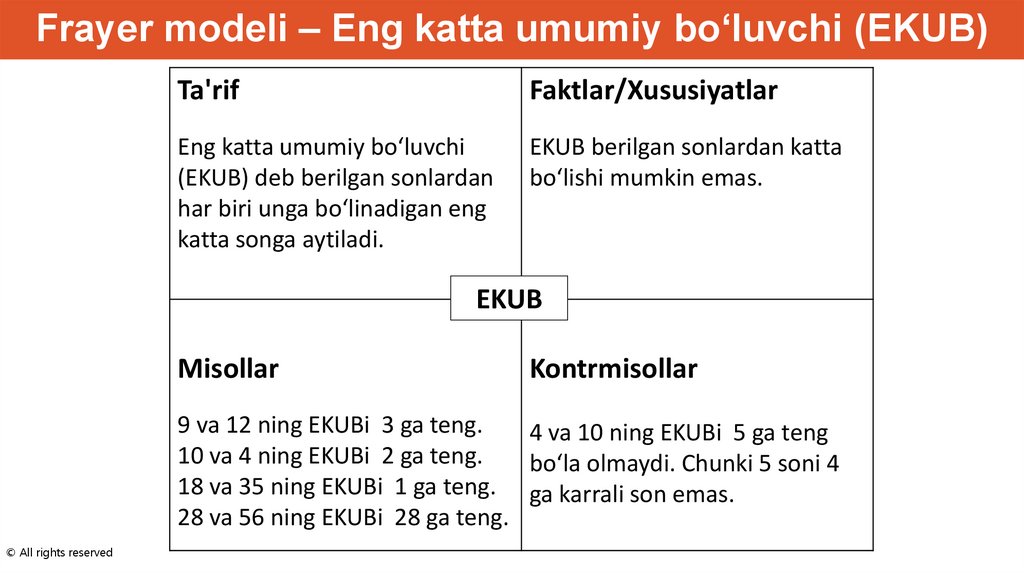
Frayer modeli – Eng katta umumiy bo‘luvchi (EKUB)
Ta'rif
Faktlar/Xususiyatlar
Eng katta umumiy bo‘luvchi
(EKUB) deb berilgan sonlardan
har biri unga bo‘linadigan eng
katta songa aytiladi.
EKUB berilgan sonlardan katta
bo‘lishi mumkin emas.
EKUB
Misollar
Kontrmisollar
9 va 12 ning EKUBi 3 ga teng.
4 va 10 ning EKUBi 5 ga teng
10 va 4 ning EKUBi 2 ga teng.
bo‘la olmaydi. Chunki 5 soni 4
18 va 35 ning EKUBi 1 ga teng. ga karrali son emas.
28 va 56 ning EKUBi 28 ga teng.
© All rights reserved

36.

Frayer modeli– Eng katta umumiy bo‘luvchi (EKUB)
Misollar
9 va 12 ning EKUBi 3 ga teng.
10 va 4 ning EKUBi 2 ga teng.
18 va 35 ning EKUBi 1 ga teng.
28 va 56 ning EKUBi 28 ga teng.
Juftlikda ishlash
• Nima uchun yuqoridagi 4 ta misollar
aynan misol sifatida tanlanganligini
tushuntirib bera olasizmi?
© All rights reserved
Source: Used with permission – Microsoft Stoc

37.

Frayer modeli – Eng katta umumiy bo‘luvchi (EKUB)
• Birinchi misol juft va toq sonlarni o‘z ichiga oladi; bu
juda odatiy hol.
Misollar
• Ikkinchi misol ikkita juft son mavjud (ikkita toq son
bo‘lishi mumkin), lekin birinchi son kattaroq; bu har
doim kichikroq sondan keyin kattaroq sonni berish
tendentsiyasiga qarshi turadi.
9 va 12 ning EKUBi 3 ga teng.
10 va 4 ning EKUBi 2 ga teng.
• Uchinchi misol EKUB 1 bo‘lishi mumkinligini ko‘rsatadi;
18 va 35 ning EKUBi 1 ga teng.
Bu berilgan sonlar o‘zaro tub bo‘lganda holatda
28 va 56 ning EKUBi 28 ga teng. bo‘ladi, bu yerda yangi tushuncha kiritilishi mumkin.
• To‘rtinchi misol EKUB berilgan sonlar juftining
kichigiga teng bo‘lishi mumkinligini ko‘rsatadi.
• Keyingi misollar uch yoki undan ortiq sonning EKUBini
topishni o‘z ichiga olishi kerak bo‘ladi.
© All rights reserved

38.

3 - mashg‘ulot
© All rights reserved
Source: Used with permission – Microsoft Stoc

39.

3 - mashg‘ulot - O‘z Frayer modelingizni yarating
1-bosqich: Guruhlarda ishlash
• Har bir guruh:
• Frayer modelini tuzish uchun biror tushunch (kontseptsiya)ni
tanlaydi.
• Aniqlik va ijodkorlikni ta’minlagan holda, bo‘laklarga
ajratilgan varaqda o‘z modelini yaratish uchun guruh a’zolari
hamkorlikda ishlaydi.
• Boshqa ishtirokchilarda Frayer modelini tushunish uchun
model haqida qisqacha izoh tayyorlaydi.
© All rights reserved

40.

3 - mashg‘ulot - O‘z Frayer modelingizni yarating
2-bosqich: World Café aylanishlari
• Stansiyalarda almashinish:
• Har bir guruhdan bitta a’zo (taqdimotchi) tashrif buyuruvchi boshqa guruh a’zolariga
o’z Frayer modelini tushuntirish uchun o’z guruhida qoladi.
• Guruhning qolgan a'zolari belgilangan vaqt oralig‘ida (masalan, har 5 daqiqada)
boshqa guruhga borishadi.
• Har bir guruhga tashrif buyuruvchilar boshqa Frayer modellari bilan tanishadilar va
o’z fikrlarini bildiradilar yoki savollar beradilar.
• Fikr-mulohazalarni yig‘ish:
• Muhokama vaqtida guruh ishtirokchilari savollar, sharhlar yoki g‘oyalarni stiker
qog‘ozlarga yozib yopishtiradilar yoki to‘g‘ridan-to‘g‘ri bo‘laklarga bo‘lingan
modelning tegishli bo’laklariga yozadilar.
© All rights reserved

41.

3 - mashg‘ulot - O‘z Frayer modelingizni yarating
3-bosqich: Guruh ishtirokchilari bilan o‘zaro qisqacha muhokama
qilish (10 daqiqa)
• Guruhlar o‘zlarining dastlabki joylarida qayta yig‘ilishadi.
• Taqdimotchi olingan fikrlar va savollar bilan o‘rtoqlashadi.
• Barcha guruhlar to‘plangan ma'lumotlar asosida yangicha fikrlar
yoki g‘oyalarni muhokama qiladilar.
© All rights reserved

42.

O‘quvchilar uchun Frayer modeli
Faol o'rganishni rag'batlantirish uchun
o'qituvchilar quyidagilarni amalga
oshirishlari kerak :
1. O‘quvchilar uchun xotirada saqlash va qayta ko‘rib chiqish uchun
yordam sifatida to‘liq Frayer modellarini namuna sifatida
yaratish.
2. Tugallanmagan Frayer modellarini taqdim eting. “Misollar” va
“Kontrmisollar”dagi qismlarni bo‘sh qoldiring. Shunda
o‘quvchilar o‘zlari ham to‘liq model yaratishlari mumkin
(Watson & Mason, 2005). O‘quvchilar o‘zlarining “Misollar” va
“Kontrmisollar” bandlarini sinfdoshlari baholashlari uchun
almashishlari mumkin.
3. O‘qituvchining yetarlicha ko‘rsatmalari bilan o‘quvchilar sinfda
o‘z fikrini namoyish qilishi uchun noldan boshlab o‘zlarining
Frayer modellarini yaratishlari mumkin. Bu esa qisqa vaqtda
Source: Used with permission – Microsoft Stoc
takrorlash va qayta ko‘rib chiqishni osonlashtiradi.

43.

Tushlik
Source: Used with permission – Microsoft Stock Image

44.

Tushunchalarni
ifodalash
usullari
© All rights reserved
Source: Used with permission – Microsoft Stoc

45.

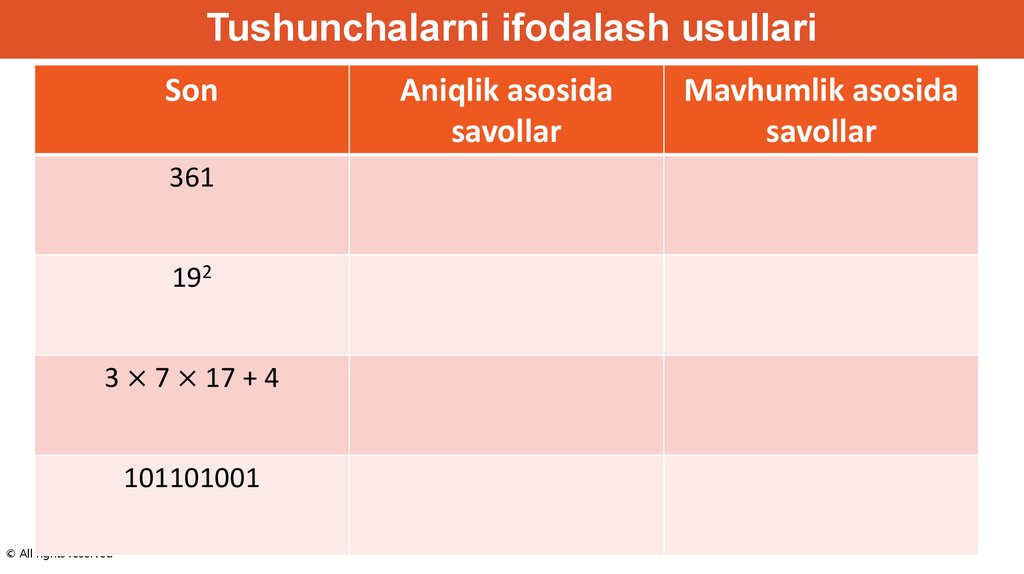
Tushunchalarni ifodalash usullari
Quyidagi sonlarga e’tibor bering:
361; 192 ; 3 × 7 × 17 + 4 ; 101101001
Guruhlarda ishlash
• Ushbu sonlarning har biri qanday o‘ziga xoslikka ega deb o‘ylaysiz?
• Sonlarning har biri uchun qanday oson yoki murakkab savollarni berishingiz
mumkin? (Zazkis, 2011) (Vong, 2015)
Son
354
© All rights reserved
Oson savollar
• Ushbu sonda nechta raqam bor?
• Ushbu son juftmi yoki toq sonmi?
Murakkab savollar
• Ushbu son tubmi yoki
murakkab sonmi?

46.

Tushunchalarni ifodalash usullari
Son
361
192
3 × 7 × 17 + 4
101101001
© All rights reserved
Aniqlik asosida
savollar
Mavhumlik asosida
savollar

47.

Tushunchalarni ifodalash usullari
Son
361
192
Oson savollar
Murakkab savollar
• Ushbu sonda nechta raqam bor? • Ushbu son tubmi yoki
• Ushbu son juftmi yoki toq sonmi?
murakkab sonmi?
• Ushbu son biror sonning
• Ushbu son o‘nli kasr
kvadratimi?
shaklida nechta raqamdan
• Ushbu sonning ko‘paytuvchilari
iborat bo‘ladi?
qaysilar?
3 × 7 × 17 + 4
• Ushbu son juftmi yoki toq sonmi? • Ushbu son o‘nli kasr
shaklida nechta raqamdan
iborat bo‘ladi?
101101001
Ikkilik sanoq sistemasida nechta
raqam bor?
© All rights reserved
• Ushbu son o‘nli kasr
shaklida nechta raqamdan
iborat bo‘ladi?

48.

Tushunchalarni ifodalash usullari
• Tushunchalarning aniqlik asosida bo‘lishiga turli ko‘rinish
va omillar ta'sir qiladi.
• Sonlarni turli usullar yordamida ifodalash, turli
savollarga javob berish uchun ishlatilishi mumkin
bo‘lgan turli xususiyatlarni bildiradi.
© All rights reserved

49.

Funksiyalarni
ifodalash
usullari
© All rights reserved
Source: Used with permission – Microsoft Stoc

50.

Funksiyalarni ifodalash usullari
Keling eslab o‘taylik:
• Sizningcha, quyidagi uchta kvadrat funksiyalarning qanday
bog‘liqlik jihatlari bor?
• Buni qanday bildingiz?
y = 3x2 – 12x + 9
y = 3(x – 2)2 – 3
y = 3(x – 1)(x – 3)
(6-Trening: Matematik fikrlashni rivojlantirish uchun
mazmunli o‘quv tajribalarini loyihalash (1-qism))
© All rights reserved

51.

Funksiyalarni ifodalash usullari
Keling eslatib ko‘raylik:
• Xuddi shu kvadrat funksiyalarning quyidagi ko‘rinishlarida qanday
aniqliklarni anglash mumkin?
a) y = 3x2 – 12x + 9
O‘quvchilar funksiya grafigi OY o‘qini (0;9) nuqtada kesib o‘tishini
ko‘rishlari mumkin.
b) y = 3(x – 2)2 – 3
Funksiyaning eng kichik qiymati -3 ga teng qiymatiga ega bo‘lishi
aniqdir.
c) y = 3(x – 1)(x – 3)
O‘quvchilar funksiya grafigi OX o‘qini (1;0) va (3;0) nuqtalarda kesib
o‘tishini ko‘rishlari mumkin.
© All rights reserved

52.

Funksiyalarni ifodalash usullari
• Samarali o‘qitishda bir xil tushunchalarning ifodalashining turli xil ifodalash
usullari qo‘llanilishi kerak.
• Bu bizning doimiy matematika sinfimizning odatiy dars o‘tish usulimizga
aylanishi kerak.
• Bolalar bog‘chasidan 11-sinfgacha bo‘lgan o‘quv dasturlari barcha o‘quvchilarga
quyidagilarga imkon berishi kerak:
• matematik g‘oyalarni tartibga solish, ko‘chirib olish va muhokama qilish
uchun ifodalash va ulardan foydalanish
• muammolarni hal qilish uchun matematik ifodalarni tanlash, qo‘llash va
moslashtirish
• fizik, ijtimoiy va matematik hodisalarni modellashtirish va izohlash uchun
ifodalardan foydalanish. (NCTM, 2000, 67-bet)
• Keyinchalik matematika darslarida bir nechta tasvirlardan qanday samarali
foydalanish mumkinligini ko‘rib chiqamiz.
© All rights reserved

53.

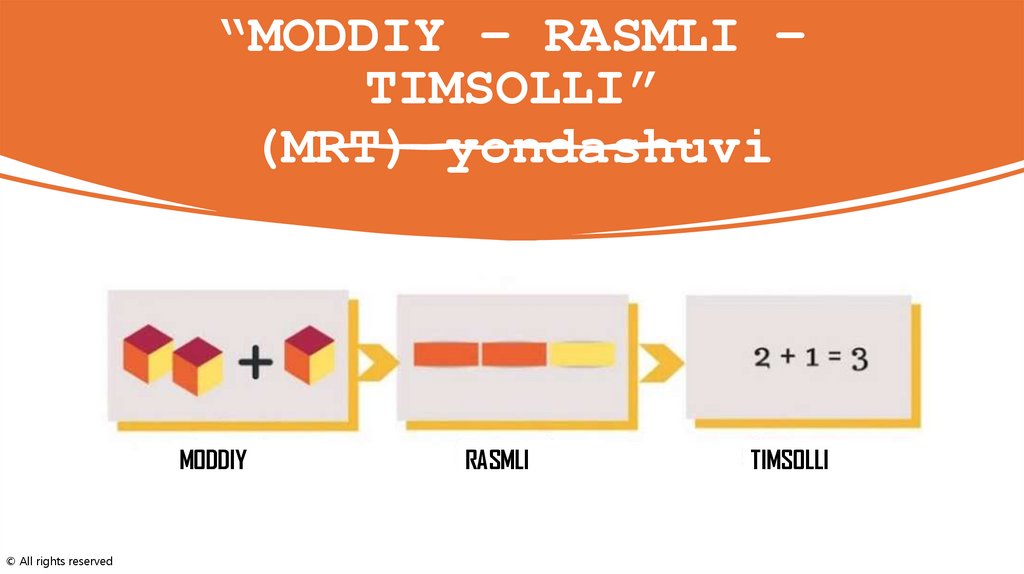
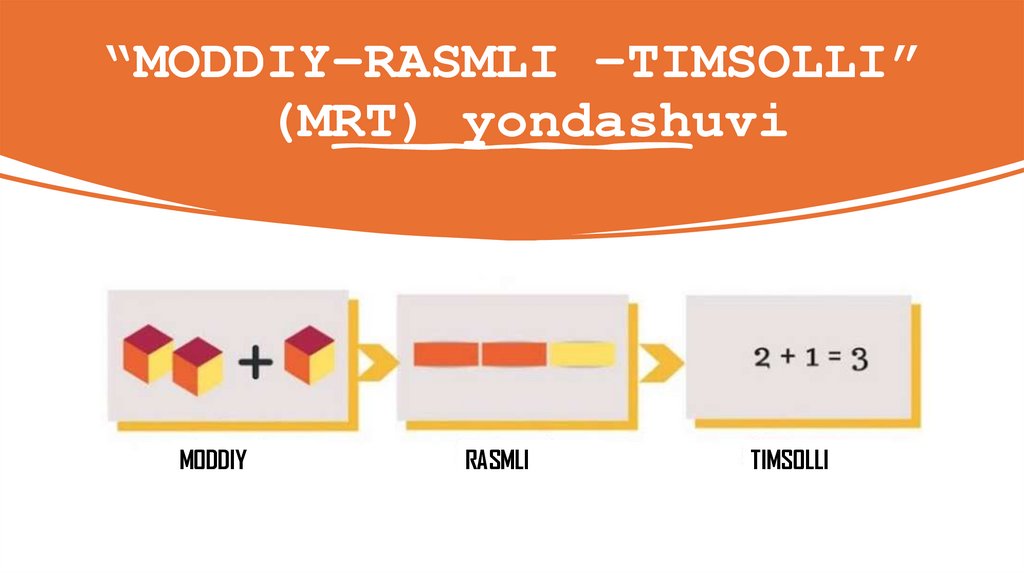
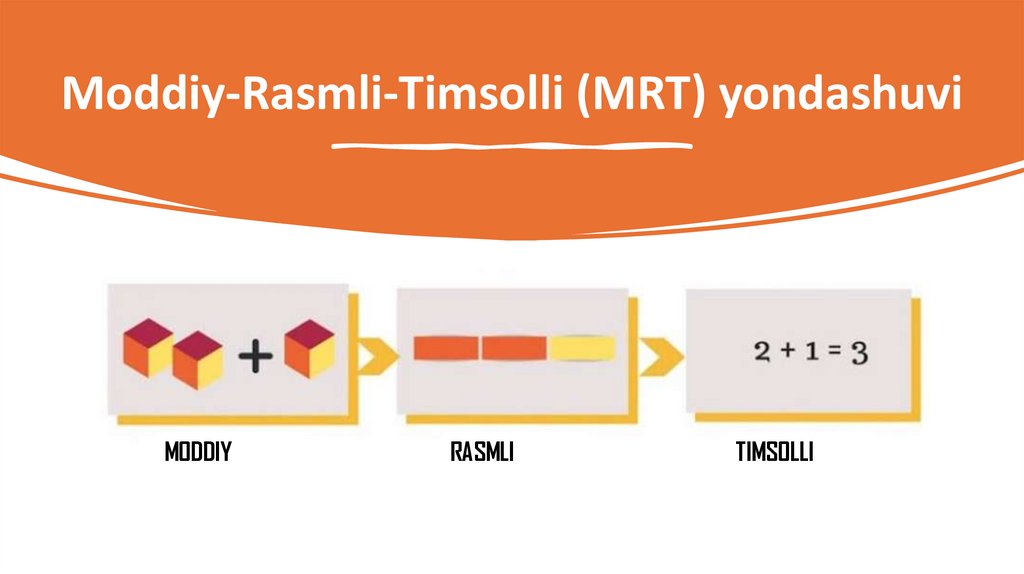
“MODDIY – RASMLI –
TIMSOLLI”
(MRT) yondashuvi
MODDIY
© All rights reserved
RASMLI
TIMSOLLI

54.

Tanaffus
Source: Used with permission – Microsoft Stoc

55.

O‘tilganlarni
mustahkamlash
Source: Used with permission – Microsoft Stoc

56.

Olingan bilimlarni kelajakda ishlatish
O'rganishni amaliyot bilan bog‘lash - bugungi ta'lim jarayoni o'qituvchilar tayyorgarligini
qanday o‘zagartirishini o'rganing
Mazmun:
• Quyidagi savollar ustida mulohaza yuriting
• Siz uchun bugun o'rgangan qaysi uchta asosiy tushuncha yoki strategiyalar eng
samarali bo‘ldi?
• Qanday qilib bu tushunchalar sizning matematikani o'qitish va o'rganish haqidagi
hozirgi tamoyillaringizga mos keladi yoki aksincha?
• Siz uchun bugungi muhokama yoki mashg'ulotlarning qaysi lahzasi “aha” bo'ldi?
• Topshiriq (o'ylang-juftlikda ishlash-ulashish-kvadrat)
• O'ylab ko'ring: javoblaringizni yozish uchun 5 daqiqa vaqt sarflang.
• Juftlikda ishlash: mulohazalaringizni sherigingiz (juftingiz) bilan muhokama qiling.
• Kvadrat: stol atrofida guruhda mulohazalaringizni umumlashtiring va auditoriya bilan
o‘rtoqlashing
© All rights reserved

57.

Olingan bilimlarni kelajakda ishlatish
O'rganishni amaliyot bilan bog‘lash - bugungi ta'lim jarayoni o'qituvchilar tayyorgarligini qanday
o‘zagartirishini o'rganing
Mazmun:
• Yo'naltiruvchi savollar
• Tumaningizdagi o'qituvchilar bilan ushbu strategiyalarni baham ko'rganda qanday qiyinchiliklarga duch
kelishingiz mumkin?
• Bugungi mashg'ulotdagi qaysi misollar, vositalar yoki o'xshashliklar o'qituvchilarga ushbu konsepsiyalarni
yanada samaraliroq tushunishga yordam berishi mumkin?
• Bugungi olgan bilimlaringizni ta'lim jarayoniga integratsiya qilish uchun qanday aniq harakatlarni amalga
oshirasiz?
• Keyingi qadamlar (individual ishlash)
• O'qituvchilaringizga bitta kontseptsiya yoki strategiyani (masalan, Frayer modeli) qanday taqdim etishingiz
haqida qisqacha reja tuzing.
• Bu kontseptual tushunishni yoki umumiy o'qitish muammolarini hal qilishini qanday qo'llab-quvvatlashi
ko‘rsating.
© All rights reserved

58.

Guruh taqdimotlari
© All rights reserved

59.

Bugungi darsning maqsadlari:
MRT yondashuvi bosqichlari
O'quvchilarga yondashuv mohiyatining har
bir qadamni o‘z o‘rnida qo‘llashni
tushuntirish va o‘zlashtirishga yordam berish
uchun “Moddiy-Rasmiy-Timsolli” (MRT)
yondashuvidan foydalanish.
Bosqichma-bosqichi mas’uliyatni o’tkazish
Bosqichma-bosqich mas’uliyatni o’tkazishdan
foydalanish tizimi, o‘quvchilarning o‘qituvchi
ko‘rsatmalaridan tushunchalarni mustaqil
o‘zlashtira olishlarini qo‘llab-quvvatlashini
ko‘rsatish.
Source: Used with permission – Microsoft Stock Image

60.

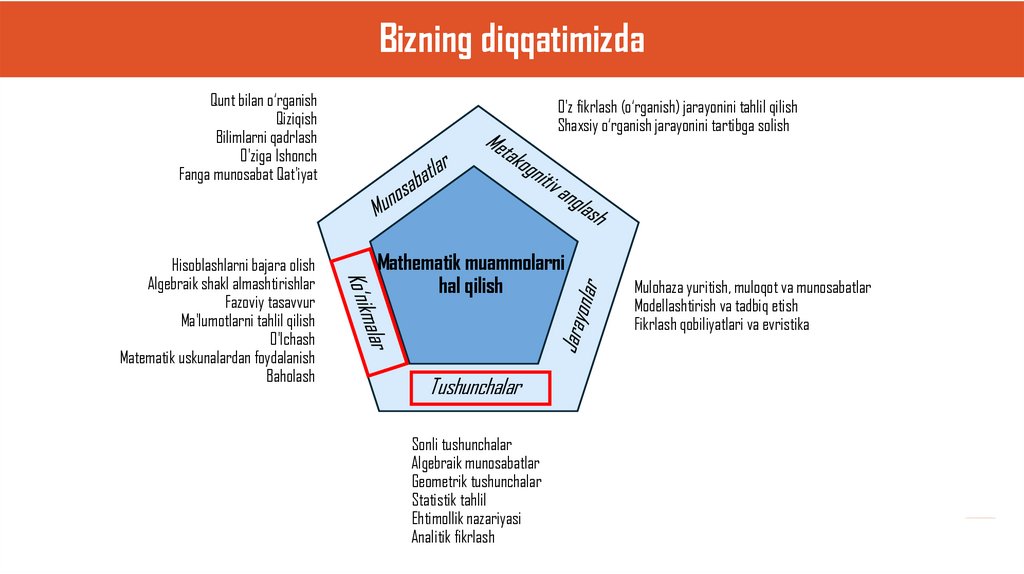
Bizning diqqatimizda
Qunt bilan o‘rganish
Qiziqish
Bilimlarni qadrlash
O'ziga Ishonch
Fanga munosabat Qat'iyat
Hisoblashlarni bajara olish
Algebraik shakl almashtirishlar
Fazoviy tasavvur
Ma'lumotlarni tahlil qilish
O'lchash
Matematik uskunalardan foydalanish
Baholash
O'z fikrlash (o‘rganish) jarayonini tahlil qilish
Shaxsiy o‘rganish jarayonini tartibga solish
Mathematik muammolarni
hal qilish
Tushunchalar
Sonli tushunchalar
Algebraik munosabatlar
Geometrik tushunchalar
Statistik tahlil
Ehtimollik nazariyasi
Analitik fikrlash
Mulohaza yuritish, muloqot va munosabatlar
Modellashtirish va tadbiq etish
Fikrlash qobiliyatlari va evristika

61.

4- mashg‘ulot
Source: Used with permission – Microsoft Stoc

62.

4 - mashg‘ulot – Kartalardan ikkitani tanlang
1
2
3
4
5
6
7
8
9

63.

4 - mashg‘ulot – Kartalardan ikkitasini tanlang
1
2
3
4
5
6
7
8
9

64.

4 - mashg‘ulot – Muhokama qiling (Guruhlarda ishlash )
Nima deb o‘ylaysiz natija
tasodifmi?
Source: Used with permission – Microsoft Stock Image

65.

4 - mashg‘ulot – Muhokama qiling va taqdimot orqali namoyish
eting
• Men bir-biridan 2 ga farq qiladigan 2 ta
kartani tanladim. Bu holda ayirma har
doim ham 18 ga teng edi.
• Bu ketma-ketlikning umumiy hadini topish
uchun shu shaklni davom ettira olasizmi?
• Qanday ketma-ketlikni ko‘rdingiz?
© All rights reserved

66.

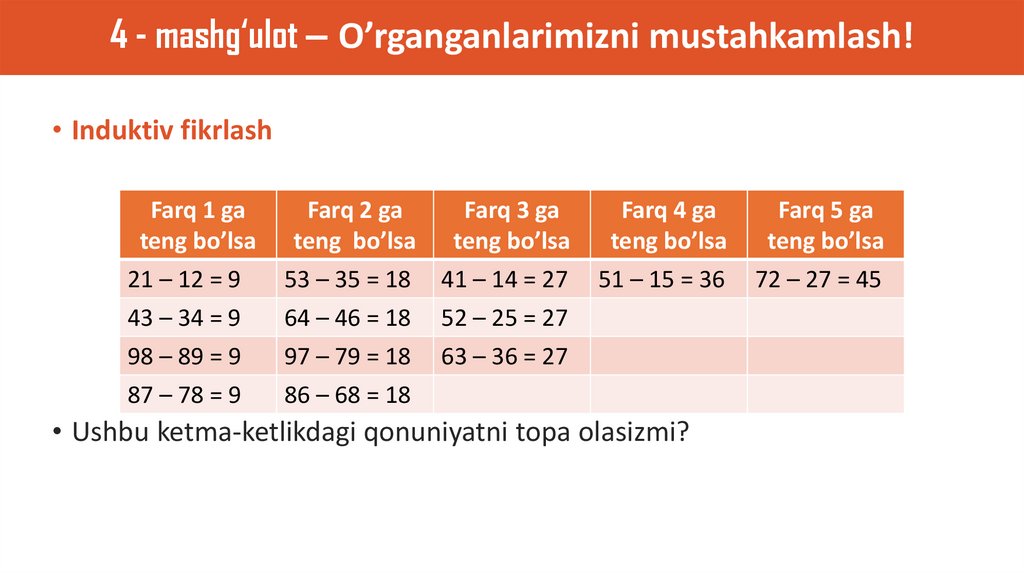
4 - mashg‘ulot – O’rganganlarimizni mustahkamlash!
• Induktiv fikrlash
Farq 1 ga
teng bo’lsa
Farq 2 ga
teng bo’lsa
Farq 3 ga
teng bo’lsa
Farq 4 ga
teng bo’lsa
Farq 5 ga
teng bo’lsa
21 – 12 = 9
43 – 34 = 9
98 – 89 = 9
53 – 35 = 18
64 – 46 = 18
97 – 79 = 18
41 – 14 = 27
52 – 25 = 27
63 – 36 = 27
51 – 15 = 36
72 – 27 = 45
87 – 78 = 9
86 – 68 = 18
• Ushbu ketma-ketlikdagi qonuniyatni topa olasizmi?

67.

Activity 4 – Consolidation
• x va y (x > y) tanlagan ishtirokchi va murabbiylarning dastlabki raqamlari
bo‘lsin.
• Tuzish mumkin bo‘lgan ikki xonali sonlar: 10x + y va 10y + x.
10x + y – (10y + x) = 10x – x + y – 10y
= 9x – 9y
= 9(x – y)

68.

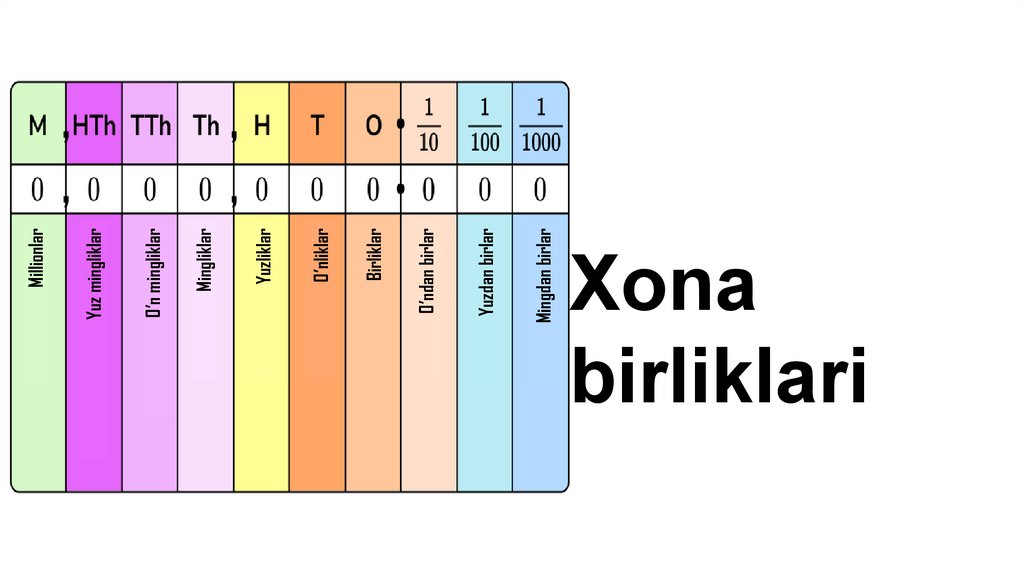
Mingdan birlar
Yuzdan birlar
O’ndan birlar
Birliklar
O’nliklar
Yuzliklar
Mingliklar
O’n mingliklar
Yuz mingliklar
Millionlar
Xona
birliklari

69.

Xona birliklari to`g`risida Youtubedagi videohangoma

70.

“MODDIY–RASMLI –TIMSOLLI”
(MRT) yondashuvi
MODDIY
RASMLI
TIMSOLLI

71.

“MODDIY–RASMLI –TIMSOLLI” (MRT) yondashuvi
MRT orqali kontseptsiyalarni ishlab
chiqishni himoya qilish:
Tasavvurni paydo qilish uchun
moddiy ko‘rgazmali qurollardan
foydalanish
Bu matematik tushunchalarni
rasmli va timsollar bilan
bog‘lang.

72.

“MODDIY–RASMLI –TIMSOLLI” (MRT) yondashuvi
Moddiy (M)
• Moddiy narsalardan foydalangan holda tushunchani
o’rganish
Rasmli (R)
• Statik rasmlar chizish
Timsolli (T)
Matematik timsollar, belgilar, qoidalar va algoritmlarni
o‘z ichiga oladi.

73.

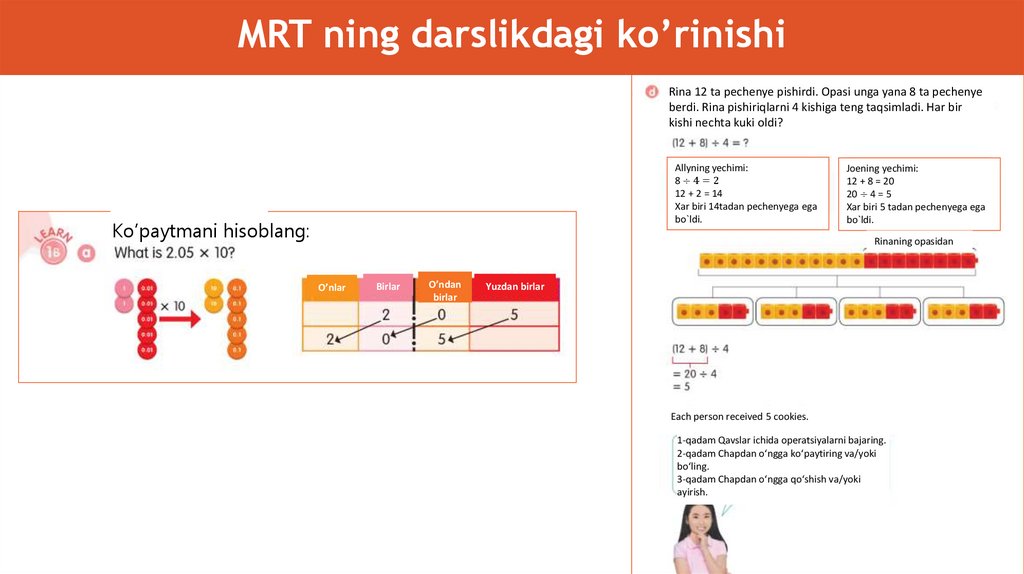
MRT ning darslikdagi ko’rinishi
Rina 12 ta pechenye pishirdi. Opasi unga yana 8 ta pechenye
berdi. Rina pishiriqlarni 4 kishiga teng taqsimladi. Har bir
kishi nechta kuki oldi?
Allyning yechimi:
8÷4=2
12 + 2 = 14
Xar biri 14tadan pechenyega ega
bo`ldi.
Ko’paytmani hisoblang:
Joening yechimi:
12 + 8 = 20
20 ÷ 4 = 5
Xar biri 5 tadan pechenyega ega
bo`ldi.
Rinaning opasidan
O’nlar
Birlar
O’ndan
birlar
Yuzdan birlar
Each person received 5 cookies.
1-qadam Qavslar ichida operatsiyalarni bajaring.
2-qadam Chapdan o‘ngga ko‘paytiring va/yoki
bo‘ling.
3-qadam Chapdan o‘ngga qo‘shish va/yoki
ayirish.
74

74.

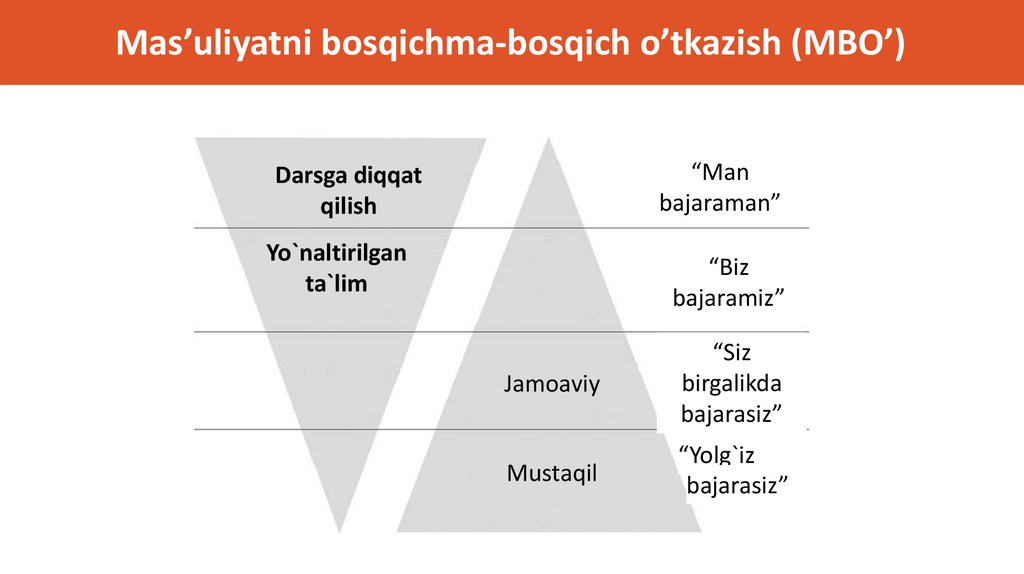
“Man
bajaraman”
Darsga diqqat
qilish
Yo`naltirilg
an ta`lim
“Biz
bajaramiz”
Jamoaviy
Mustaqil
“Siz birgalikda
bajarasiz”
“Yolg`iz
bajarasiz”
Mas’uliyatni bosqichma-bosqich
o’tkazish (MBO’) modeli
(Fisher & Frey 2008)

75.

Mas’uliyatni bosqichma-bosqich o’tkazish (MBO’) modeli
O’rganish jarayonida o’qituvchi mas’uliyatini
bosqichma-bosqich o’quvchilarga o’tkazish modeli
to‘rtta asosiy bosqichni o‘z ichiga oladi:
1) Asosiy ko’rsatma berish bosqichi:
O'qituvchi jarayonni berilgan fikr bilan
tanishtirish, ko`rsatmalar berish va uning
dolzarbligini tushuntirish orqali boshlaydi.
Ushbu bosqich aniq o‘quv maqsadlarini
belgilash va o‘quvchilar e'tiborini darsning
muhim jihatlariga yo‘naltirish uchun juda
muhimdir. Bu o‘quvchilarning kontseptsiyani
tushunishi va qo‘llashi uchun asos yaratadi.

76.

Mas’uliyatni bosqichma-bosqich o’tkazish (MBO’) modeli
2) Yo`naltirilgan ko`rsatma berish bosqichi:
Bu bosqichda oʻqituvchi asosiy yo’lboshchi bo‘ladi,
faol tarzda o‘quvchilarga ko‘rsatmalar, savollar
beradi va muhokamalar olib boradi. O’qituvchilar
o‘quvchilariga ma’lumotlarni tushunish va unga
jalb qilishni oshiradigan topshiriqlar ustida
ishlashlariga yordam beradi.

77.

Mas’uliyatni bosqichma-bosqich o’tkazish (MBO’) modeli
3) Jamoaviy o`rganish bosqichi:
Bu yerda o‘quvchilar guruh bo`lib topshiriq
bajarishadi, o‘rganganlarini tengdoshlari bilan
hamkorlikda qo‘llaydilar. Zarur bo‘lganda
o‘qituvchining ko‘magida o‘quvchilar umumiy
o‘quv muhitida muammolarni hal qilish,
munozaralarda qatnashish va fikr almashish
orqali o‘z tushunchalarini yanada
mustahkamlaydi.

78.

Mas’uliyatni bosqichma-bosqich o’tkazish (MBO’) modeli
4) Mustaqil o`rganish bosqichi:
Bu bosqichda o‘quvchilar tushunchalarni mustaqil
qo`llash qobilyatini namoyon etadilar. Asosiy
e'tibor mustaqil amaliyotga qaratilgan bo‘lib, unda
talabalar o‘z ko‘nikmalarini yangi kontekstlarda
ishlatadilar, ma'lumotlarni sintez qiladilar va o‘z
tushunchalarini aniqlaydilar. Ushbu bosqich
o‘quvchilarda o‘ziga ishonch va malaka oshirishga
urg‘u beradi.

79.

Mas’uliyatni bosqichma-bosqich o’tkazish (MBO’) modeli
“Man
bajaraman”
Darsga diqqat
qilish
Yo`naltirilgan
ta`lim
“Biz
bajaramiz”
Jamoaviy
“Siz
birgalikda
bajarasiz”
Mustaqil
“Yolg`iz
bajarasiz”

80.

Tanaffus
© All rights reserved
Source: Used with permission – Microsoft Stoc

81.

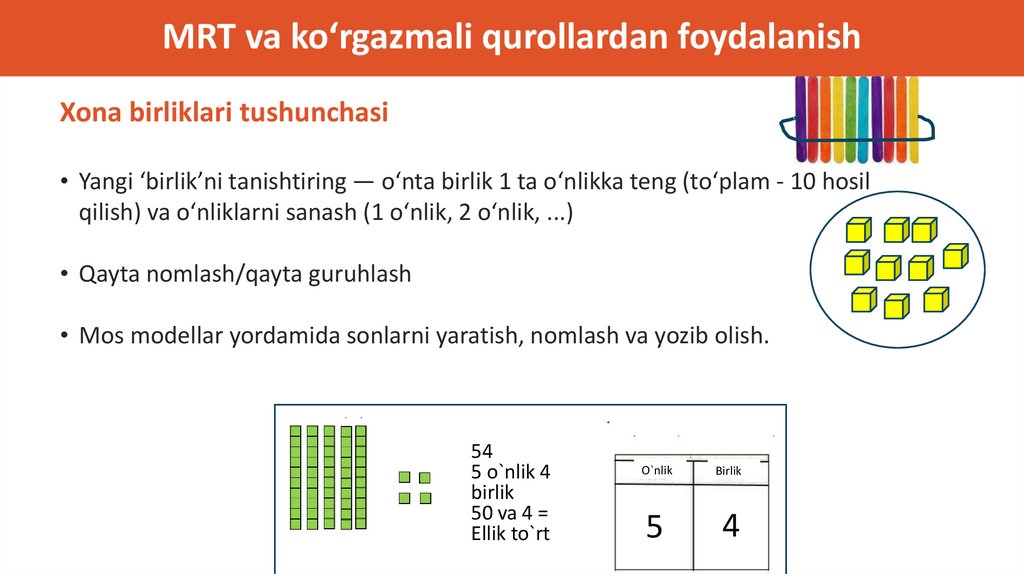
MRT va ko‘rgazmali qurollardan foydalanish
Xona birliklari tushunchasi
• Yangi ‘birlik’ni tanishtiring — o‘nta birlik 1 ta o‘nlikka teng (to‘plam - 10 hosil
qilish) va o‘nliklarni sanash (1 o‘nlik, 2 o‘nlik, ...)
• Qayta nomlash/qayta guruhlash
• Mos modellar yordamida sonlarni yaratish, nomlash va yozib olish.
54
5 o`nlik 4
birlik
50 va 4 =
Ellik to`rt
O`nlik
Birlik
5
4

82.

5 xonali sonlarni solishtirish va
tartiblash
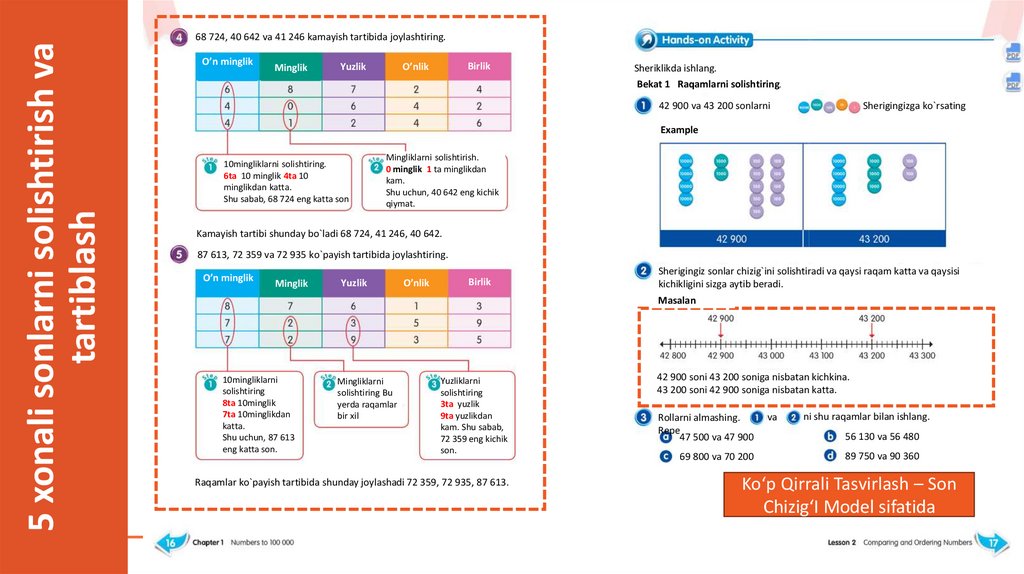
68 724, 40 642 va 41 246 kamayish tartibida joylashtiring.
O’n minglik
Minglik
Birlik
O’nlik
Yuzlik
Sheriklikda ishlang.
Bekat 1 Raqamlarni solishtiring.
Sherigingizga ko`rsating
42 900 va 43 200 sonlarni
Example
10mingliklarni solishtiring.
6ta 10 minglik 4ta 10
minglikdan katta.
Shu sabab, 68 724 eng katta son
Mingliklarni solishtirish.
0 minglik 1 ta minglikdan
kam.
Shu uchun, 40 642 eng kichik
qiymat.
Kamayish tartibi shunday bo`ladi 68 724, 41 246, 40 642.
87 613, 72 359 va 72 935 ko`payish tartibida joylashtiring.
O’n minglik
Minglik
Yuzlik
O’nlik
Birlik
Sherigingiz sonlar chizig`ini solishtiradi va qaysi raqam katta va qaysisi
kichikligini sizga aytib beradi.
Masalan
10mingliklarni
solishtiring
8ta 10minglik
7ta 10minglikdan
katta.
Shu uchun, 87 613
eng katta son.
Mingliklarni
solishtiring Bu
yerda raqamlar
bir xil
Yuzliklarni
solishtiring
3ta yuzlik
9ta yuzlikdan
kam. Shu sabab,
72 359 eng kichik
son.
Raqamlar ko`payish tartibida shunday joylashadi 72 359, 72 935, 87 613.
42 900 soni 43 200 soniga nisbatan kichkina.
43 200 soni 42 900 soniga nisbatan katta.
Rollarni almashing.
Repeat
47 500 va 47 900
69 800 va 70 200
va
ni shu raqamlar bilan ishlang.
56 130 va 56 480
89 750 va 90 360
Ko‘p Qirrali Tasvirlash – Son
Chizig‘I Model sifatida
83

83.

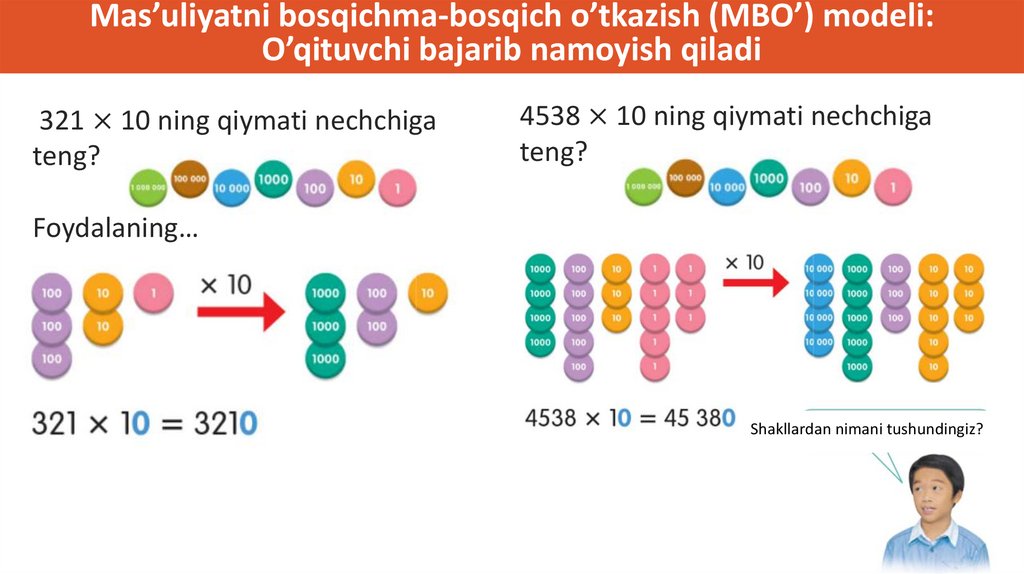
Mas’uliyatni bosqichma-bosqich o’tkazish (MBO’) modeli:
O’qituvchi bajarib namoyish qiladi
321 × 10 ning qiymati nechchiga
teng?
4538 × 10 ning qiymati nechchiga
teng?
Foydalaning…
Use
Shakllardan nimani tushundingiz?
84

84.

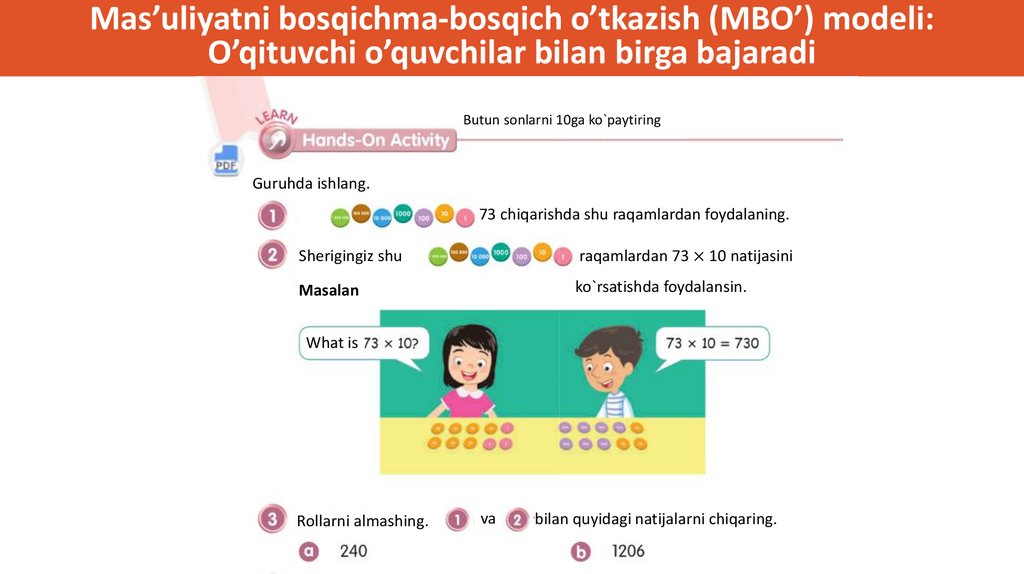
Mas’uliyatni bosqichma-bosqich o’tkazish (MBO’) modeli:
O’qituvchi o’quvchilar bilan birga bajaradi
Butun sonlarni 10ga ko`paytiring
Guruhda ishlang.
73 chiqarishda shu raqamlardan foydalaning.
Sherigingiz shu
raqamlardan 73 × 10 natijasini
Masalan
ko`rsatishda foydalansin.
What is
Rollarni almashing.
va
bilan quyidagi natijalarni chiqaring.

85.

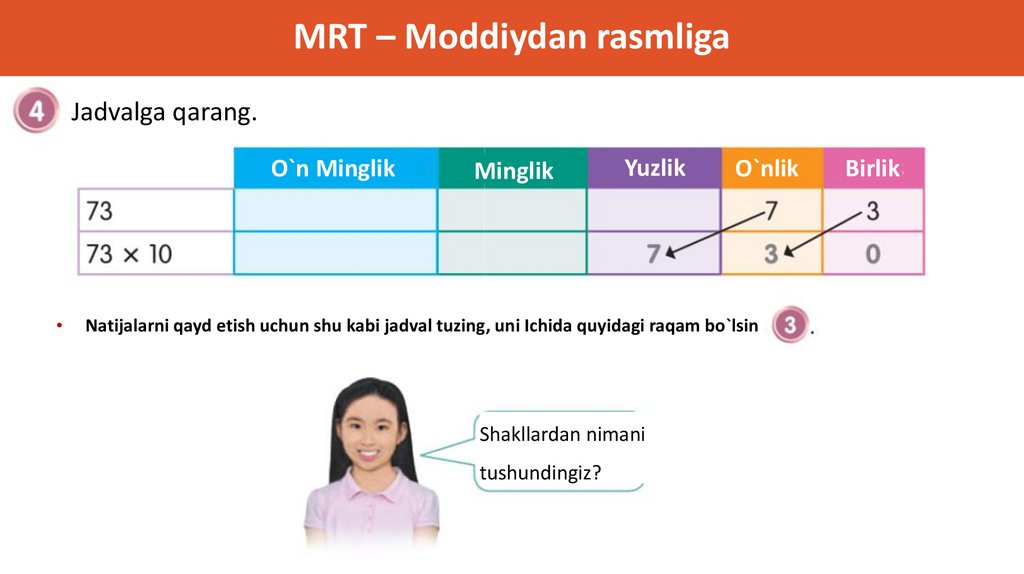
MRT – Moddiydan rasmliga
Jadvalga qarang.
O`n Minglik
Minglik
Yuzlik
O`nlik
Birlik
Natijalarni qayd etish uchun shu kabi jadval tuzing, uni Ichida quyidagi raqam bo`lsin
Shakllardan nimani
tushundingiz?
© All rights reserved
86

86.

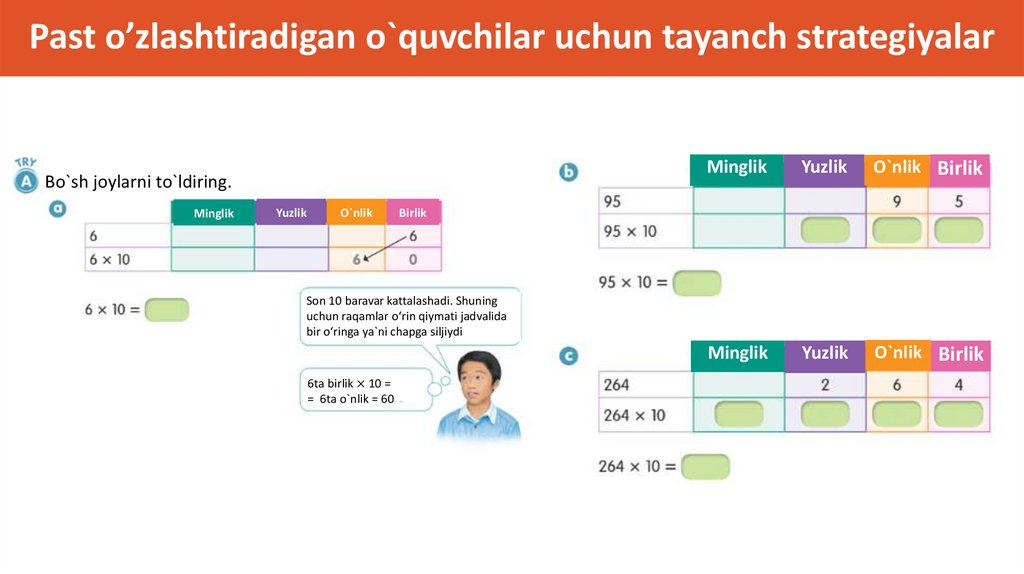
Past o’zlashtiradigan o`quvchilar uchun tayanch strategiyalar
Bo`sh joylarni to`ldiring.
Minglik
Yuzlik
O`nlik
Minglik
Yuzlik
O`nlik Birlik
Minglik
Yuzlik
O`nlik Birlik
Birlik
Son 10 baravar kattalashadi. Shuning
uchun raqamlar o‘rin qiymati jadvalida
bir o‘ringa ya`ni chapga siljiydi
6ta birlik × 10 =
= 6ta o`nlik = 60

87.

MRT usulida
4 ta amalni
bajarish

88.

5 - mashg‘ulot
Source: Used with permission – Microsoft Stoc

89.

5-Mashg`ulot – Ko’paytmani turli usullarda topish
12 × 3 ko’paytmani qanday
usullarda topa olasiz?
Source: Used with permission – Microsoft S

90.

Ko’paytmani turli usullarda topish
12 × 3 ko’paytmani qanday usullarda topa olasiz?
Sonli tugmalar
Qiymat
Algoritm

91.

6 - mashg‘ulot
Source: Used with permission – Microsoft Stoc

92.

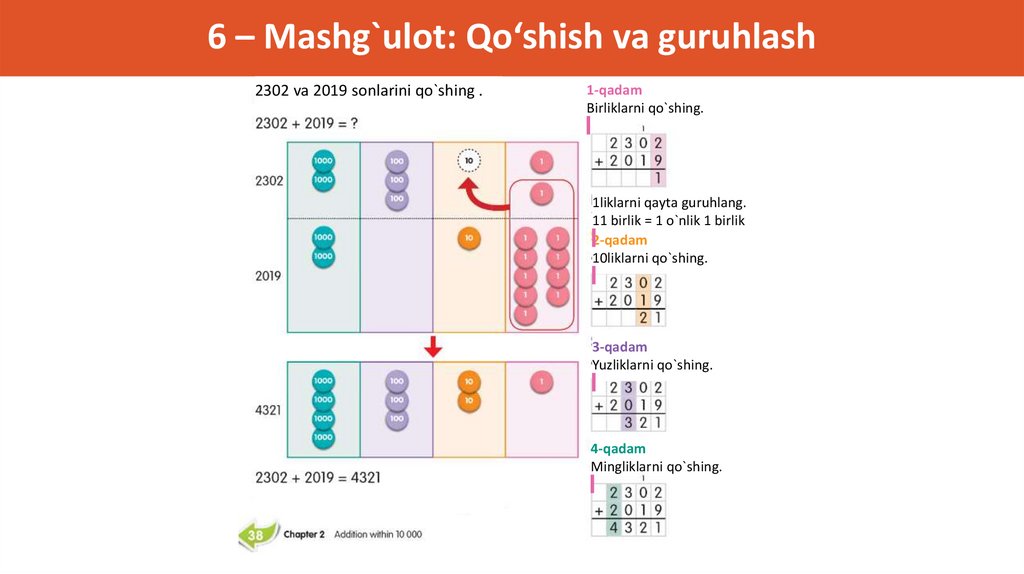
6 – Mashg`ulot: Birliklar va o‘nliklarda qo‘shish hamda guruhlash
2302 + 2019

93.

6 – Mashg`ulot: Qo‘shish va guruhlash
2302 va 2019 sonlarini qo`shing .
1-qadam
Birliklarni qo`shing.
1liklarni qayta guruhlang.
11 birlik = 1 o`nlik 1 birlik
2-qadam
10liklarni qo`shing.
3-qadam
Yuzliklarni qo`shing.
4-qadam
Mingliklarni qo`shing.

94.

7 - mashg‘ulot
Source: Used with permission – Microsoft Stoc

95.

7 – Mashg`ulot: Qo‘shish va guruhlash
Mashg‘ulotni bajarish uchun bir-biringizga
o‘rgatish uchun guruhlarda ishlang.
A guruh: 7064 + 2378 = ?
B guruh: 7064 – 2378 = ?

96.

8 - mashg‘ulot
Source: Used with permission – Microsoft Stoc

97.

8 – Mashg`ulot: Ko`paytirish va Guruhlash
223 ni 5 ga ko‘paytiring.

98.

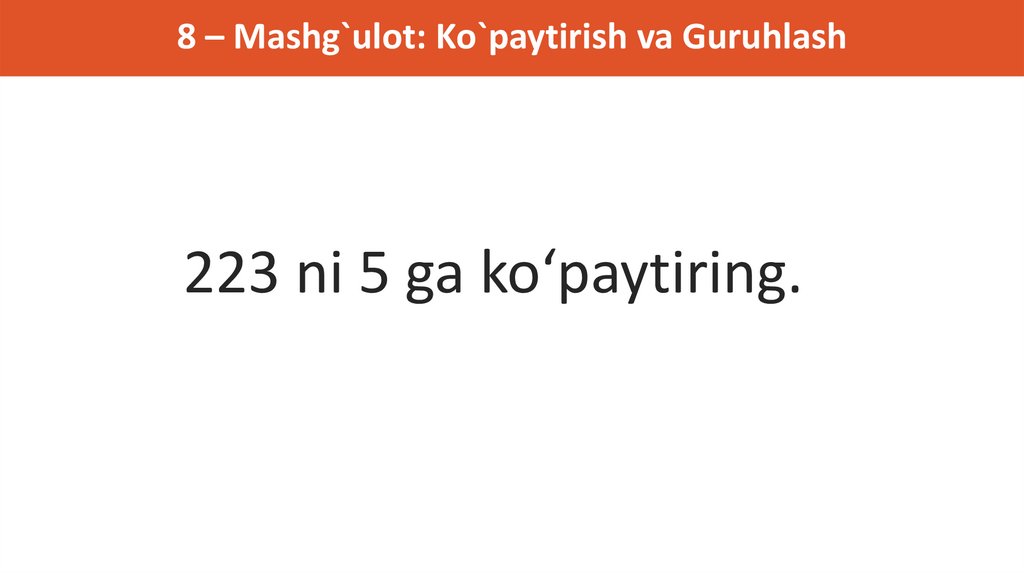
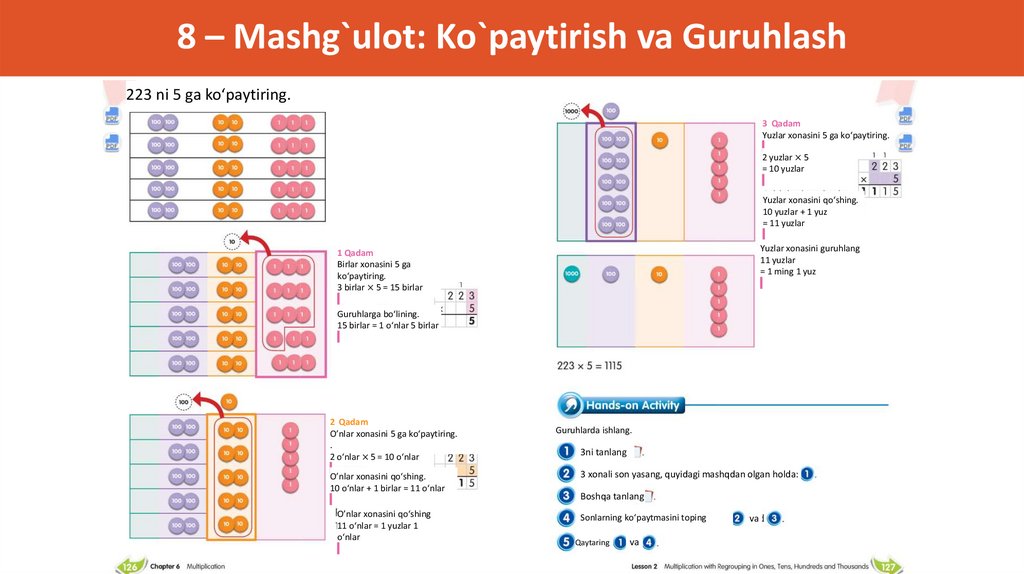
8 – Mashg`ulot: Ko`paytirish va Guruhlash
223 ni 5 ga ko‘paytiring.
3 Qadam
Yuzlar xonasini 5 ga ko‘paytiring.
2 yuzlar × 5
= 10 yuzlar
Yuzlar xonasini qo‘shing.
10 yuzlar + 1 yuz
= 11 yuzlar
Yuzlar xonasini guruhlang
11 yuzlar
= 1 ming 1 yuz
1 Qadam
Birlar xonasini 5 ga
ko‘paytiring.
3 birlar × 5 = 15 birlar
Guruhlarga bo‘lining.
15 birlar = 1 o‘nlar 5 birlar
2 Qadam
O’nlar xonasini 5 ga ko‘paytiring.
.
2 o‘nlar × 5 = 10 o‘nlar
O’nlar xonasini qo‘shing.
10 o‘nlar + 1 birlar = 11 o‘nlar
O’nlar xonasini qo‘shing
11 o‘nlar = 1 yuzlar 1
o‘nlar
Guruhlarda ishlang.
3ni tanlang
3 xonali son yasang, quyidagi mashqdan olgan holda:
Boshqa tanlang
Sonlarning ko‘paytmasini toping
Qaytaring
va
va

99.

9 - mashg‘ulot
Source: Used with permission – Microsoft Stoc

100.

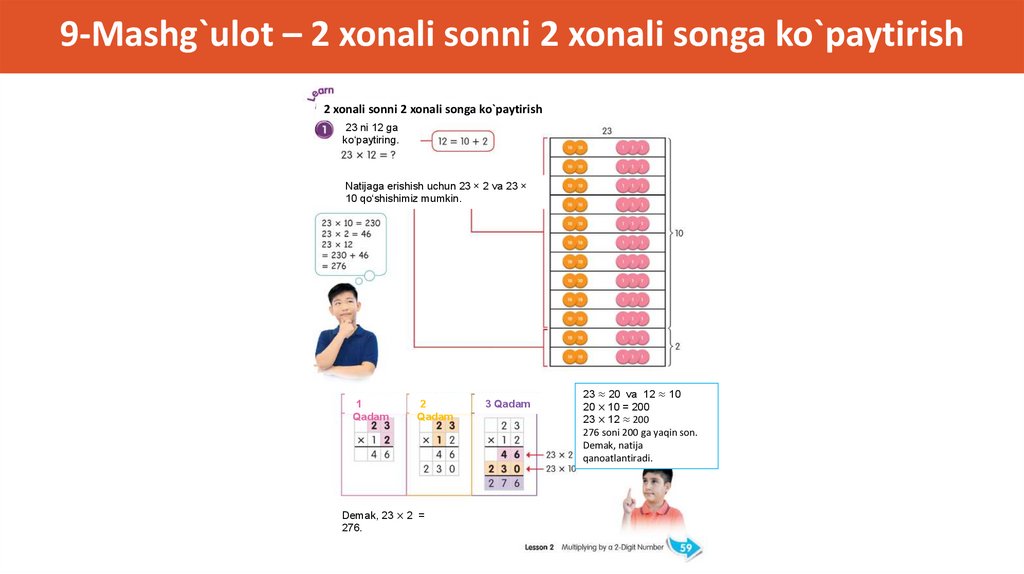
9-Mashg`ulot – 2 xonali sonni 2 xonali songa ko`paytirish
23 × 12
ko‘paytiring.

101.

9-Mashg`ulot – 2 xonali sonni 2 xonali songa ko`paytirish
2 xonali sonni 2 xonali songa ko`paytirish
23 ni 12 ga
ko‘paytiring.
Natijaga erishish uchun 23 × 2 va 23 ×
10 qo‘shishimiz mumkin.
1
Qadam
2
Qadam
Demak, 23 × 2 =
276.
3 Qadam
23 ≈ 20 va 12 ≈ 10
20 × 10 = 200
23 × 12 ≈ 200
276 soni 200 ga yaqin son.
Demak, natija
qanoatlantiradi.

102.

10 - mashg‘ulot
Source: Used with permission – Microsoft Stoc

103.

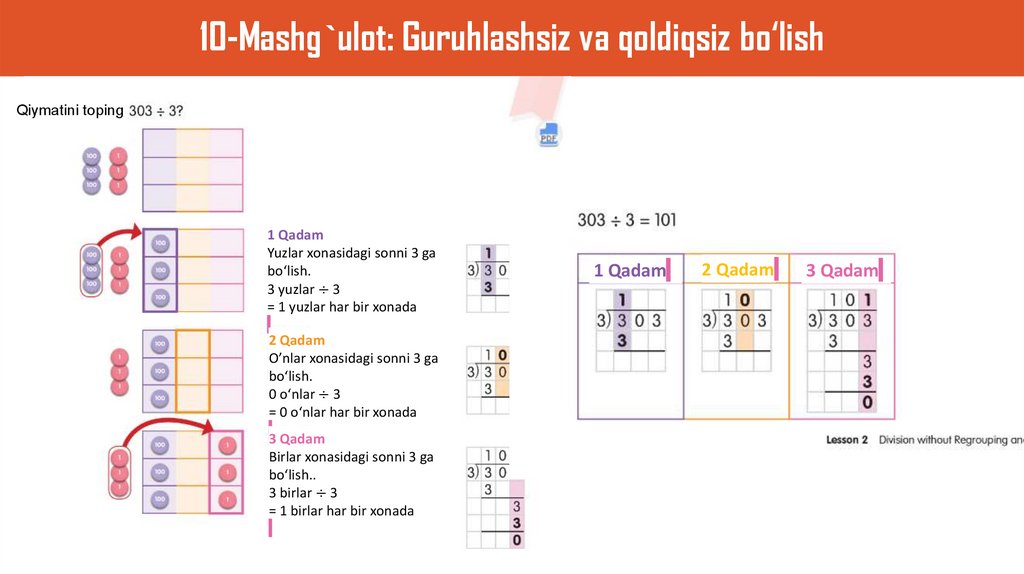
10-Mashg`ulot: Guruhlashsiz va qoldiqsiz bo‘lish
303 ÷ 3 = ?

104.

10-Mashg`ulot: Guruhlashsiz va qoldiqsiz bo‘lish
Qiymatini toping
1 Qadam
Yuzlar xonasidagi sonni 3 ga
bo‘lish.
3 yuzlar ÷ 3
= 1 yuzlar har bir xonada
2 Qadam
O’nlar xonasidagi sonni 3 ga
bo‘lish.
0 o‘nlar ÷ 3
= 0 o‘nlar har bir xonada
3 Qadam
Birlar xonasidagi sonni 3 ga
bo‘lish..
3 birlar ÷ 3
= 1 birlar har bir xonada
1 Qadam
2 Qadam
3 Qadam

105.

11 - mashg‘ulot
Source: Used with permission – Microsoft Stoc

106.

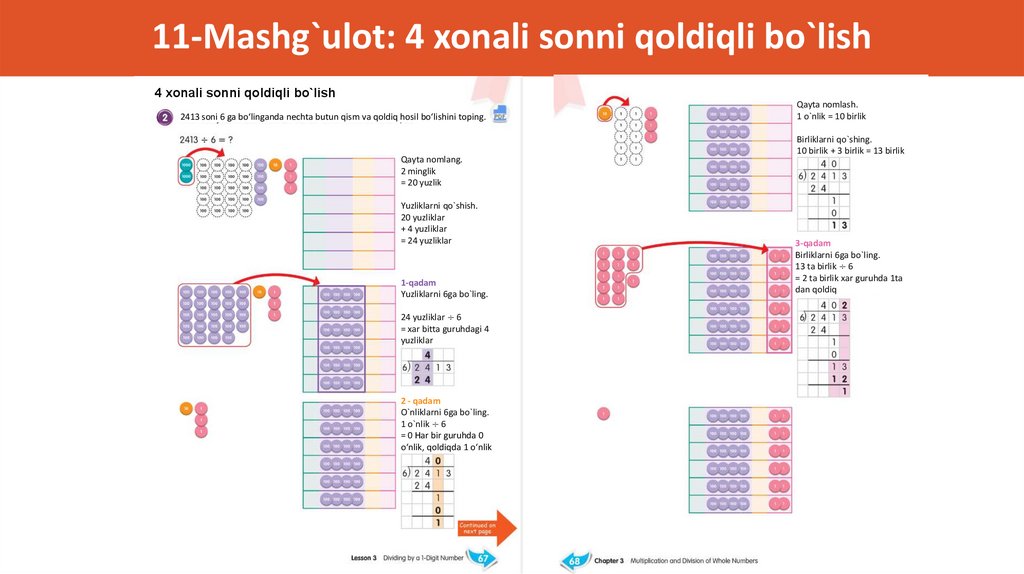
11-Mashg`ulot: 4 xonali sonni qoldiqli bo`lish
2413 ni 6 ga qoldiqli bo‘ling.

107.

11-Mashg`ulot: 4 xonali sonni qoldiqli bo`lish
4 xonali sonni qoldiqli bo`lish
2413 soni 6 ga bo‘linganda nechta butun qism va qoldiq hosil bo‘lishini toping.
Qayta nomlang.
2 minglik
= 20 yuzlik
Yuzliklarni qo`shish.
20 yuzliklar
+ 4 yuzliklar
= 24 yuzliklar
1-qadam
Yuzliklarni 6ga bo`ling.
24 yuzliklar ÷ 6
= xar bitta guruhdagi 4
yuzliklar
2 - qadam
O`nliklarni 6ga bo`ling.
1 o`nlik ÷ 6
= 0 Har bir guruhda 0
o‘nlik, qoldiqda 1 o‘nlik
Qayta nomlash.
1 o`nlik = 10 birlik
Birliklarni qo`shing.
10 birlik + 3 birlik = 13 birlik
3-qadam
Birliklarni 6ga bo`ling.
13 ta birlik ÷ 6
= 2 ta birlik xar guruhda 1ta
dan qoldiq

108.

Tanaffus
© All rights reserved
Source: Used with permission – Microsoft Stoc

109.

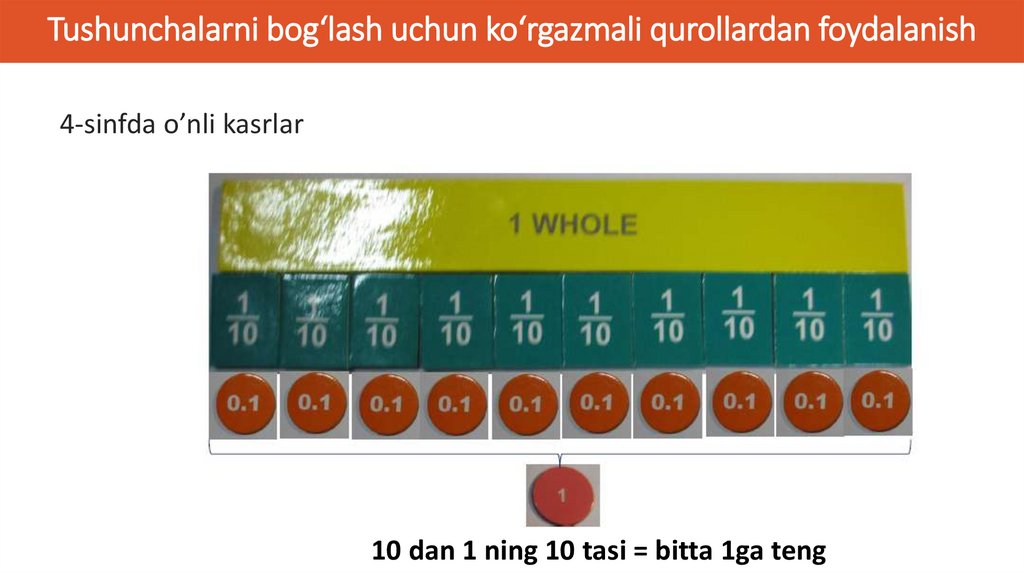
Tushunchalarni bog‘lash uchun ko‘rgazmali qurollardan foydalanish
4-sinfda o’nli kasrlar
10 dan 1 ning 10 tasi = bitta 1ga teng

110.

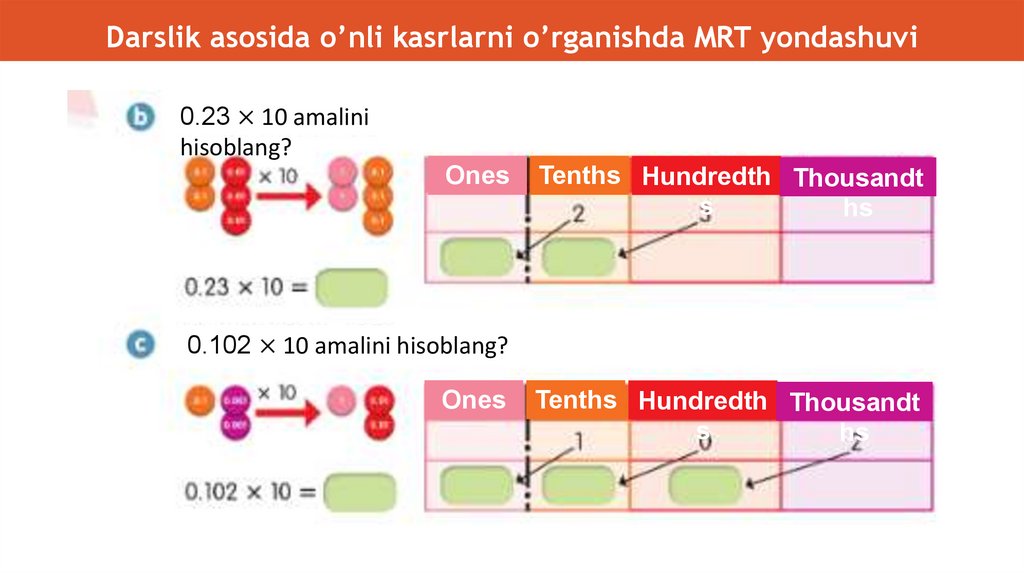
Darslik asosida o’nli kasrlarni o’rganishda MRT yondashuvi
0.23 × 10 amalini
hisoblang?
Ones
Tenths Hundredth Thousandt
s
hs
0.102 × 10 amalini hisoblang?
Ones
Tenths Hundredth Thousandt
s
hs

111.

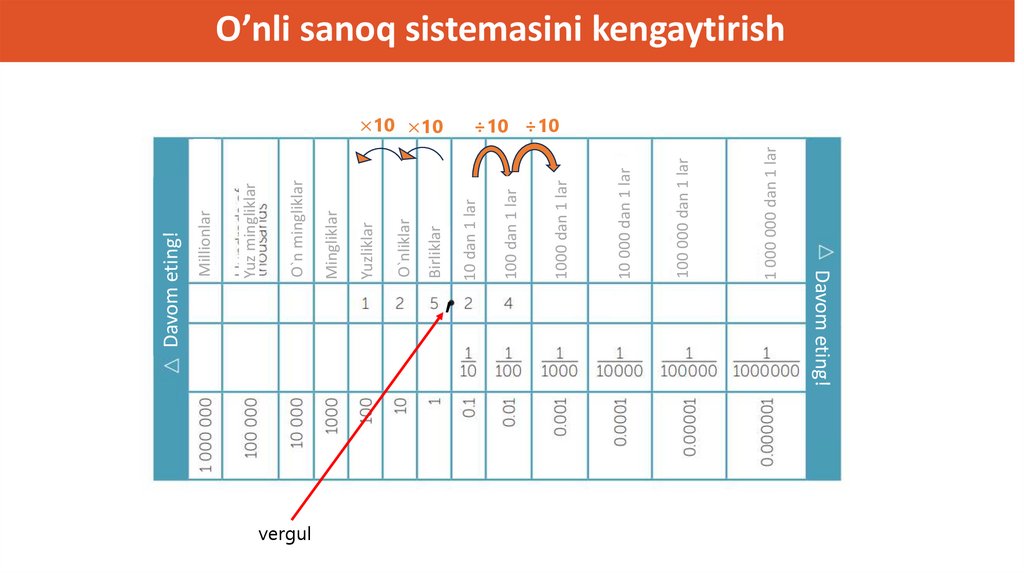
Birliklar
Ones
O`nliklar
Yuzliklar
,
1 000 000 dan 1 lar
100 000 dan 1 lar
10 000 dan 1 lar
1000 dan 1 lar
100 dan 1 lar
10 dan 1 lar
×10 ×10
Davom eting!
vergul
Mingliklar
O`n mingliklar
Yuz mingliklar
Millionlar
Davom eting!
O’nli sanoq sistemasini kengaytirish
÷10 ÷10

112.

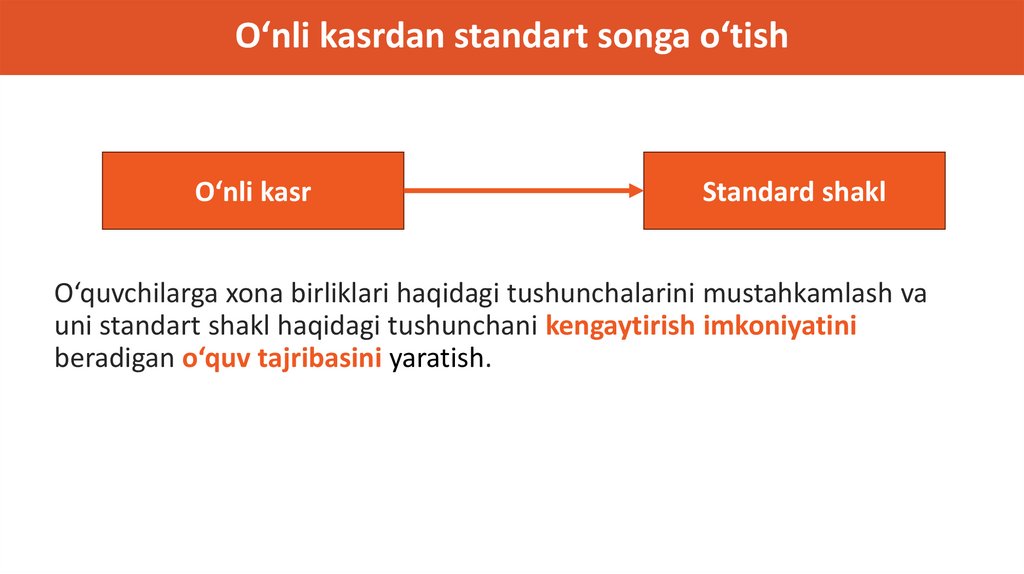
O‘nli kasrdan standart songa o‘tish
O‘nli kasr
Standard shakl
O‘quvchilarga xona birliklari haqidagi tushunchalarini mustahkamlash va
uni standart shakl haqidagi tushunchani kengaytirish imkoniyatini
beradigan o‘quv tajribasini yaratish.

113.

Sonning standard shakli
• Katta va kichik sonlarni qisqacha ifodalashda qiyinchiliklar
mavjud.
• Misol: 12 450 000
• Kengaytirilgan ko‘rinish: 1 × 10⁷ + 2 × 10⁶ + 4 × 10⁵ + 5 × 10⁴
• Misol: 0,000045
• Kengaytirilgan ko‘rinish: 4 × 10⁻⁵ + 5 × 10⁻⁶
• Sonning standart shakl:
Ta'rif: a × 10ⁿ, bu yerda 1 ≤ a < 10, va n butun son.

114.

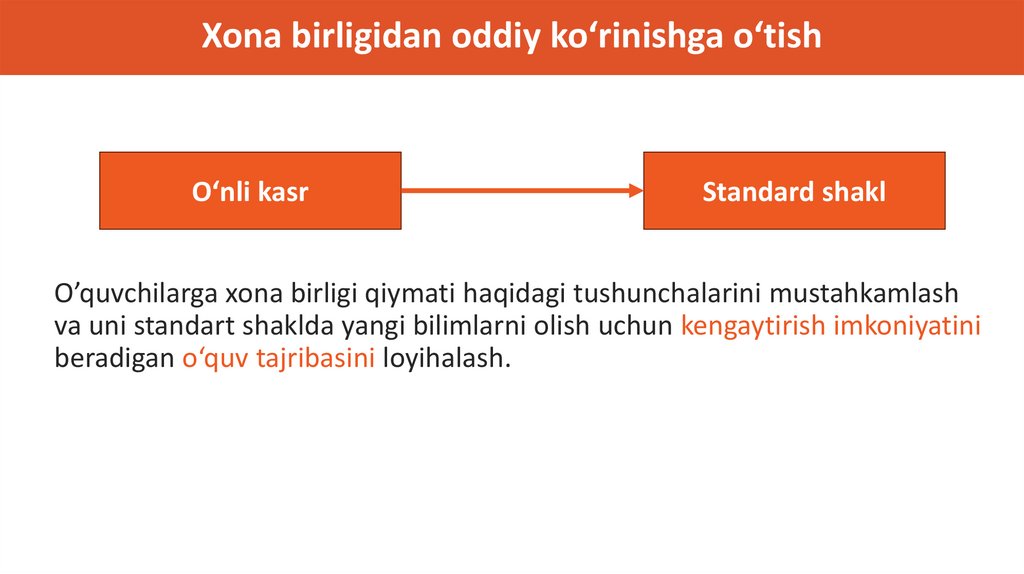
Xona birligidan oddiy ko‘rinishga o‘tish
O‘nli kasr
Standard shakl
O’quvchilarga xona birligi qiymati haqidagi tushunchalarini mustahkamlash
va uni standart shaklda yangi bilimlarni olish uchun kengaytirish imkoniyatini
beradigan o‘quv tajribasini loyihalash.

115.

O‘nli kasr
O'qituvchi va o‘quvchilar rol o‘ynashi
O'quvchilarga son qiymatlari orqali
standart ko‘rinishni tushunishga
yordam beradigan o‘quv tajribasi
Standard shakl

116.

Guruh
taqdimoti
Source: Used with permission – Microsoft Stoc

117.

Asosiy Xulosalar
Xona birliklari asos sifatida
O'qituvchilarning kengroq matematik tushunchalarni,
shu jumladan standart shaklni tushunishlarini
qo‘llab-quvvatlaydigan muhim katta g‘oya sifatida
xona birliklari qiymatini anglash.
“MRT” yondashuvi o‘rganishni kuchaytiradi
MRT yondashuvi moddiy, rasmli va timsolli
ko’rinishlarni birlashtirib, o‘quvchilarning xona
birliklari qiymati va standart shakl haqida chuqur
kontseptual tushunchani shakllantirishni ta'minlaydi.
Source: Used with permission – Microsoft Stock Image
Strukturaviy ta'lim uchun MBO’ yondashuvi
MBO’ yondashuvi orqali o‘quvchilarni yo‘naltirilgan
o‘rganishdan mustaqil qo‘llashga samarali o‘tkazadi,
bu esa murakkab mavzularni o‘zlashtirish imkonini
beradi.

118.

Bugungi mashg’ulot maqsadlari
Kasr sonlarni o‘qitishda Moddiy-Rasmli-Timsolli
(MRT) yondashuvini yanada kengroq o`rganish
Mas’uliyatni bosqichma-bosqich o’tkazish (MBO’)
ning kasr sonlarni o‘rganishda o‘quvchilarning
mustaqil o`rganuvchiga aylanishdagi rolini o`rganish
Matematik munozara va mantiqiy fikrlashni
rivojlantirish uchun Muloqot harakatlari
strategiyasini qo‘llash.
Nazariy bilimlardan amaliy ko`nikmalarga
o`tkazishda ko`rgazmali qurollar va rasmlarni
samarali ishlatish
Source: Used with permission – Microsoft Stock Image

119.

Rolli o‘yin
O‘qituvchi va o‘quvchilar:
1. MRT
2. MBO’
3.Muloqot harakatlari
Source: Used with permission – Microsoft Stoc

120.

Moddiy-Rasmli-Timsolli (MRT) yondashuvi
MODDIY
RASMLI
TIMSOLLI

121.

Mas’uliyatni bosqichma-bosqich o’tkazish (MBO’)
“Man
bajaraman”
Darsga diqqat
qilish
Yo`naltirilgan
ta`lim
“Biz
bajaramiz”
Jamoaviy
“Siz
birgalikda
bajarasiz”
Mustaqil
“Yolg`iz
bajarasiz”

122.

Muloqot harakatlari

123.

Matematik fikrlashni qo'llab-quvvatlash uchun muloqot harakatlari
1-harakat: Fikrni qayta aytish
- “Demak, siz aytmoqchisizki, bu toq sonmi?”
2-harakat: Takrorlash
- “Uning aytganini o'z so'zlaringiz bilan qaytarib bera olasizmi?”
3-harakat: Mulohaza yuritish
- “Siz bunga rozi bo'lasizmi yoki norozimisiz, nima uchun?”
4-harakat: Qo`shimcha qilish
- “Kimdir bunaqa biror narsa qo'shishni xohlarmidi?”
5-harakat: Vaqt berish (kutish)
- “Bemalol bajaravering... biz kutamiz...”

124.

Kasr sonlar

125.

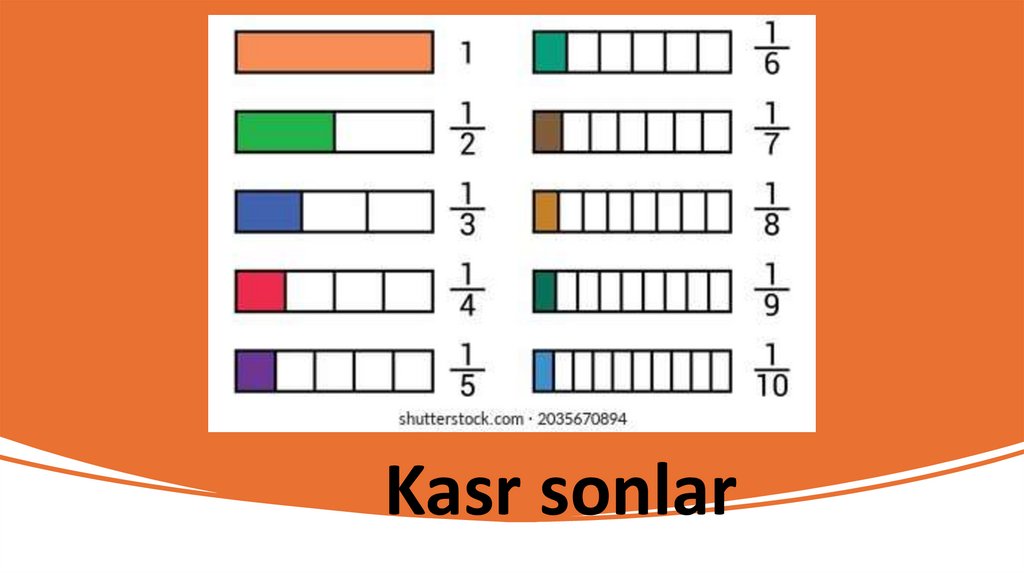
MRT yondashuvining nazariy asoslari (Jerome Bruner)
Jerome Brunerning uch xil o`rganish usuli
Moddiy narsalar
bilan qo’l
harakatlari
Rasm chizish
Jerome Bruner
Timsollar bilan
ifodalash

126.

Kasr son tushunchasining 2-sinfda o'qitilishi
• Keling, 2-sinfda o‘tiladigan kasrlar mavzusini
ko’raylik.
• Biz kasr doiralari yordamida butunning yarmi
tushunchasini yuz modeli orqali tasvirlaymiz.
Yarimni bir butunni ikki teng qismi sifatida talqin
qilamiz.
• Bu jarayonni kasrlarga oid bir nechta misollar bilan
takrorlaymiz. O‘quvchilar doiralardan foydalanib
amaliy ish olib borish jarayonida shuni kuzatdilarki,
butun qismni turli xil qismlarga bo`lish mumkin.

127.

Kasr son tushunchasining 2-sinfda o'qitilishi
• O‘quvchilarning ko`rgazmali materiallar bilan
qo’lda ishlashi orqali qator aqliy faoliyatlar
shakllanadi: dastlabki aqliy mashg`ulot
ko`rgazma materiallarining ichki tasvirini
shakllantirib olish jarayonini o`z ichiga oladi
• Ushbu tasvirlar o‘quvchilarning miyasidagi
ma’lumot markazlari sifatida xizmat qiladi, bu
esa ularga eslash va mulohaza qilish imkonini
beradi. (Butunni qismlarga bo`lish orqali kasr
tushunchasi namoyon bo`ladi)

128.

Kasr son tushunchasining 2-sinfda o'qitilishi
• Bir qancha kasr amaliyotlarini bajarish kasrlarning bir
nechta misollari bilan ishlash o`quvchi uchun ikkinchi
aqliy mashg`ulot hisoblanadi. Masalan, yarim qismi, ikki
teng qismdan tashkil topgan butun doiranining
yarimining matematik tushunchasini aks ettiradi.
• Xuddi shunday, uchta teng qismdan iborat butundan
bitta qism doiraning uchdan birining (1/3) matematik
tushunchasini aks ettiradi va hokazo.
• Bu matematik tushuncha barcha misollarda takrorlanadi.
Butunni qismlarga bo‘lish jarayoni x qiymatini aniqlaydi,
va ushbu x qiymatining bittasi 1/x sifatida ifodalanadi
(kasrlarga oid bir qancha misollar).

129.

Kasr son tushunchasining 2-sinfda o'qitilishi
• Ko`rgazmali materiallarda aks etgan matematik tushuncha tuzilmasining
jihatlariga asosiy diqqat qaratilgan bo’ladi. Misollar orasidagi umumiy
matematik tushunchalarni kuzatish va aniqlash bo‘yicha bajariladigan ushbu
mashq tajribaviy (empiric) abstraksiya deb ataladi (Skemp, 2009).
• Tajribaviy abstraksiya jarayoni bu o‘quvchi ko`rgazmali materiallar bilan
ishlayotganda yoki ichki tasvirlarni ushbu tajribalarni orqali ko`rsatib
berayotganda amalga oshish jarayoni hisoblanadi.

130.

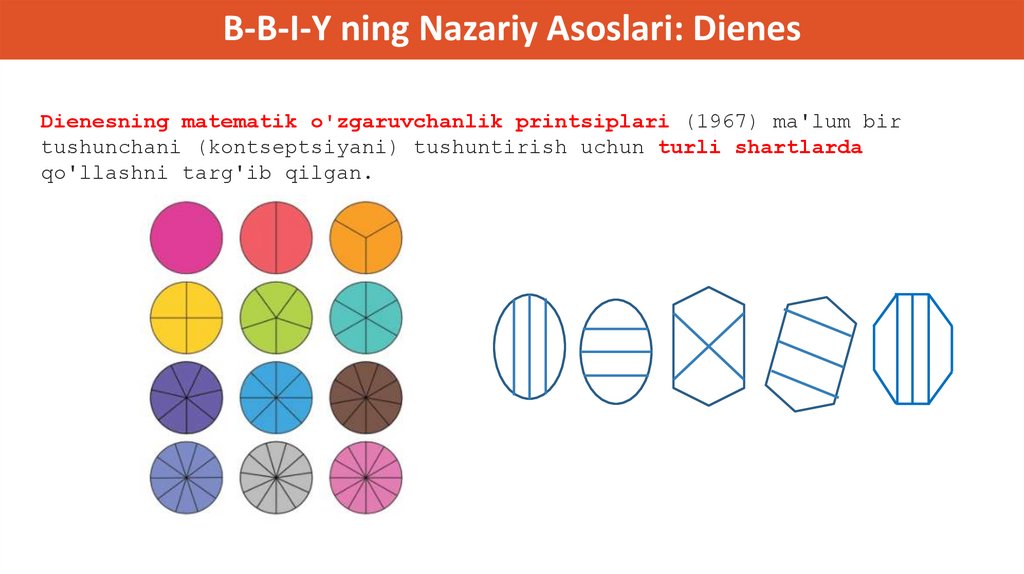
MBO’ yondashuvining nazariy asoslari (Zoltan Dienes)
Zoltan Dienes perseptual o'zgaruvchanlik prinsipida
(1967) bir tushunchani tushuntirish uchun turli xil
ko`rgazmali qurollardan foydalanishni tavsiya qilgan.
Doiraning kasr bo’laklari
Bir-biriga ulanadigan kublar
Shakl qismlari
Zoltan Dienes

131.

B-B-I-Y ning Nazariy Asoslari: Dienes
Dienesning matematik o'zgaruvchanlik printsiplari (1967) ma'lum bir
tushunchani (kontseptsiyani) tushuntirish uchun turli shartlarda
qo'llashni targ'ib qilgan.

132.

Tanaffus
Source: Used with permission – Microsoft Stoc

133.

12-Mashg`ulot
Source: Used with permission – Microsoft Stoc

134.

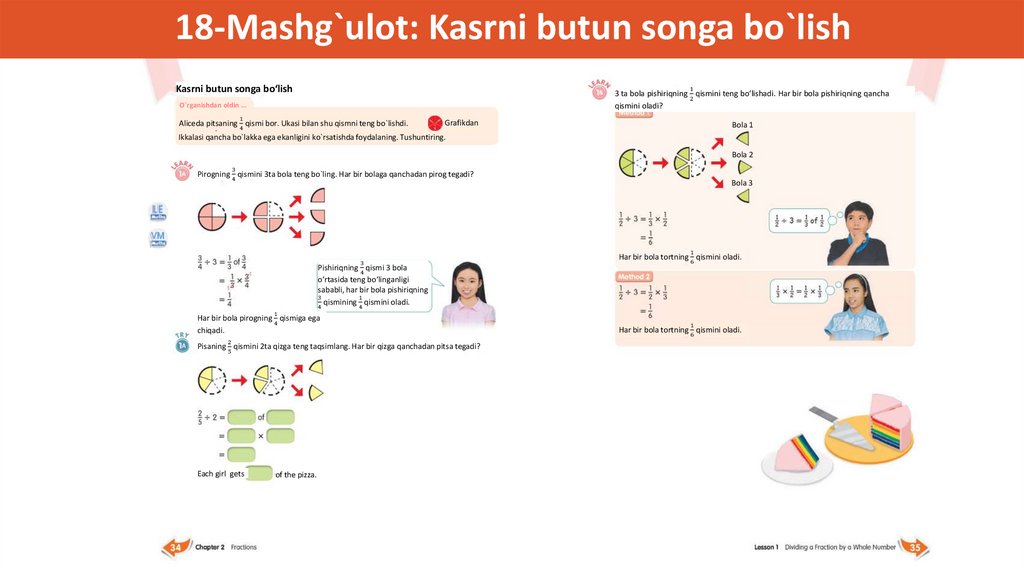
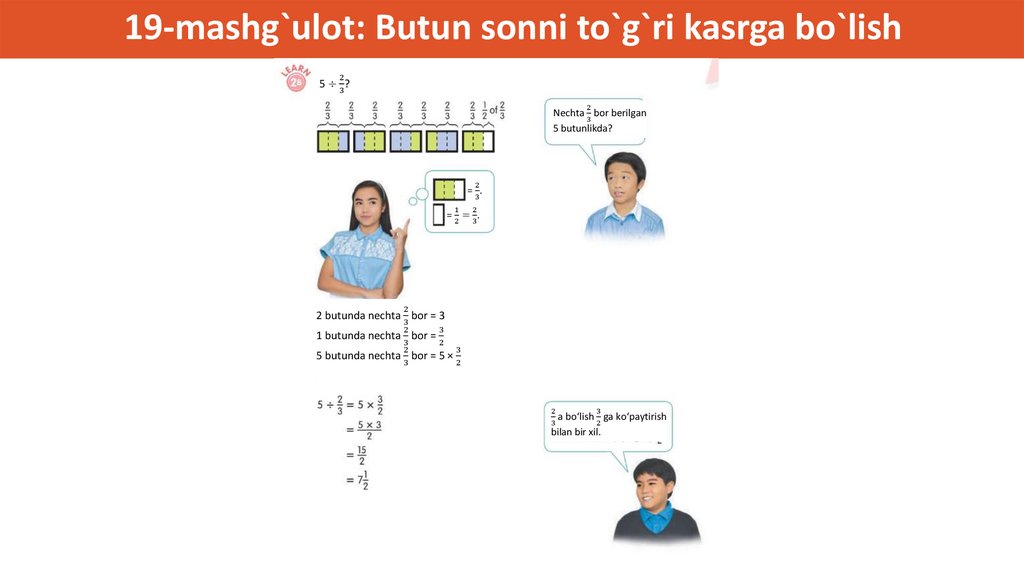
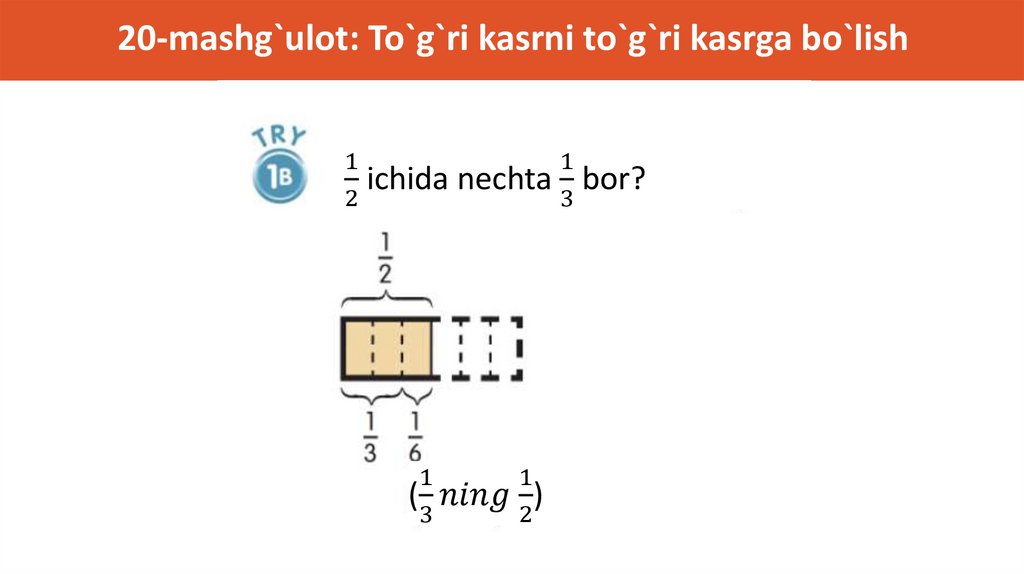
12-Mashg`ulot: Kasr sonlarni qo`shish (Qog`oz buklash)
1. Tushunchani tanishtirish
• Ikkita turli xil maxrajli kasr sonlarni qo`shish
amaliyotini bajarayotganimizni tushuntirishdan
1
1
boshlang: va .
2
3
• O`quvchilardan buni bajara olish-olmasliklari
haqida so`rang va ular bilan bu jarayon nima uchun
qiyinligini muhokama qiling
2. Qog`ozlarni tayyorlang
• O'quvchilarga kvadrat shaklidagi qog'ozni vertikal
ravishda yarmiga qayirib, so'ngra qayta ochishni
ayting.
• Qog'ozni gorizontal ravishda uch qismga buklab oling.
(Bu jarayonni ko'rsatish zarur bo'lishi mumkin.)

135.

12-Mashg`ulot: Kasr sonlarni qo`shish (Qog`oz buklash)
3. Kasr sonlarni ko`rsating