Sonli sinflar bilan ishlash. Sonli sinflar va ular bilan ishlash (complex, vallaray, slice, gslice va h.k)

1.

MUHAMMAD AL-XORAZMIY NOMIDAGI
TOSHKENT AXBOROT TEXNOLOGIYALARI UNIVERSITETI
URGANCH FILIALI
DASTURLASH
13
5
MAVZU
Ma’ruza
SonliMFC
sinflar
bilan ishlash.
OLE,
texnologiyalari.
Ko’pSonli
oynali
muhitlar
bilan
ishlash.
C++
muhitida
sinflar va
ular
bilanVisual
ishlash
(complex,
ko’p oynali
muhit
yaratish.
vallaray,
slice,
gslice
va h.k).
Ma’ruzachi
Ass. Yusupova J
DASTURLASH 1
1

2. Mа’ruza rejasi

1
Complex sonli sinf va funksiyalari.
2
Valarray sonli sinf va funksiyalari.
3
Slice va gslice sonli sinf va funksiyalari.
4
Qo’shimcha sonli sinflar.
5
Xulosa
DASTURLASH 2
•2

3.

Complex sonli sinf va funksiyalari.
C++ standarti kutubxonasidagi kompleks sonlar sinfi ob’ekt
modelidan foydalanishning yaxshi namunasidir.
Arifmetik amallar qayta aniqlash tufayli bu sinf ob’ektlari
o‘rnatilgan ma’lumot tiplaridan biriga tegishli kabi
ishlatiladi
Bundan tashqari, an’anaviy arifmetik o‘zgaruvchilar va
kompleks sonlar bir vaqtning o‘zida ixtiyoriy amallarda
ishtirok etishi mumkin
bu yerda kompleks sonlar matematikasiga oid so’z
yuritilmagan
DASTURLASH 2
3 3

4. Complex sonlar

Complex son deb: a+bi
ifodaga aytiladi, bu yerda
a va b haqiqiy sonlar,
i – mavhum birlik bo’lib, u yoki i2= -1 tengliklar bilan aniqlanadi;
a – kompleks sonning haqiqiy qismi,
bi – mavhum qismi deyiladi.
Faqat mavhum qismining ishorasi bilan farq qiladigan ikki kompleks son:
a+bi va a-bi o’zaro qo’shma deyiladi. Ko’pincha a+bi kompleks son bitta α
harfi bilan belgilanadi: α=a+bi. a+bi kompleks sonning haqiqiy qismi a=Reα
bilan, mavhum qismining koeffitsientini b=Lmα bilan belgilaydilar. α
kompleks sonning a+bi ko’rinishidagi yozuviga uning algebraik shakli
deyiladi.
DASTURLASH 2
4

5. Complex sonlar

Agar ikkita α1=a1+b1i va α2=a2+b2i kompleks sonda
a1= a2, b1= b2
bu ikki son teng deyiladi (α1= α2). Agar α=a+bi kompleks sonda a=0,
b=0 bo’lsa, bu kompleks son 0 ga (α=0) teng bo’ladi. Agar α=a+bi
kompleks sonda b=0 bo’lsa, haqiqiy son hosil bo’ladi; agar a=0 bo’lsa,
0+bi=bi sof mavhum son deyiladi.
DASTURLASH 2
5

6.

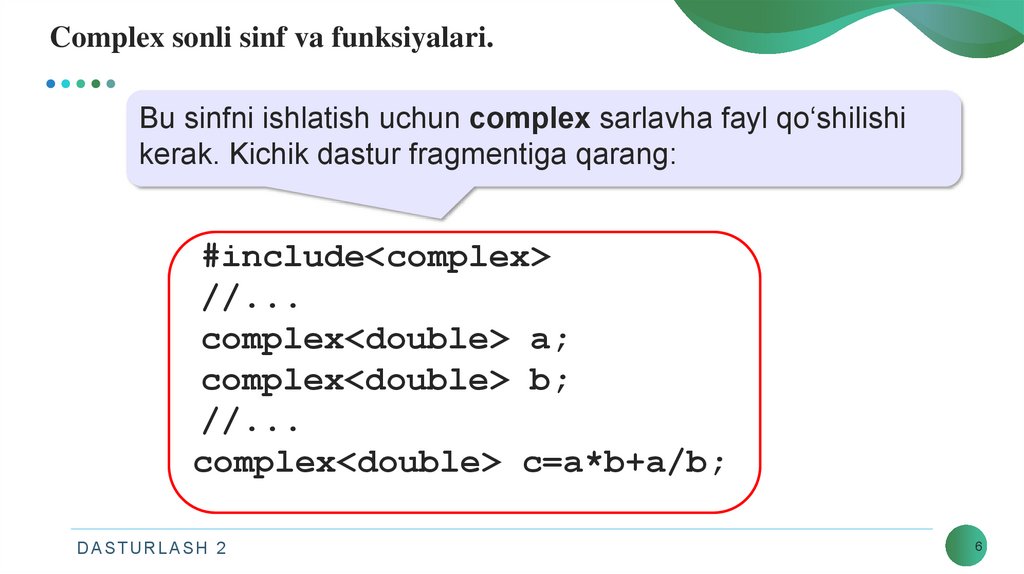
Complex sonli sinf va funksiyalari.
Bu sinfni ishlatish uchun complex sarlavha fayl qo‘shilishi
kerak. Kichik dastur fragmentiga qarang:
#include<complex>
//...
complex<double> a;
complex<double> b;
//...
complex<double> c=a*b+a/b;
DASTURLASH 2
6

7.

Complex sonli sinf va funksiyalari.
Kompleks va arifmatik amallar o‘zaro hamkorlikda
bajarailadi.:
complex<double> a;
complex<double> complex_obj=a+3.14159;
DASTURLASH 2
7

8.

Complex sonli sinf va funksiyalari.
Kompleks tiplarni arifmetik tiplar bilan ham yaratish va ular
uchun operator= ni ishlatish mumkin:
complex<double> complex_obj;
double dval=3.14159;
complex_obj=dval;
//...
int ival=3 ;
complex_obj=ival ;
DASTURLASH 2
8

9. Complex sonli sinf funksiyalari

1.real() - Bu kompleks sonning haqiqiy qismini qaytaradi.
2.imag() - Kompleks sonning mavhum qismini qaytaradi.
3.abs() - kompleks sonning absalyut qiymatini qaytaradi.
4.arg() - kompleks sonning argumentini qaytaradi
5.conj() - Bu x kompleks sonining konjugatini qaytaradi. Kompleks
sonning konjugati (real, imag) -> (real,-imag)
6.polar() - Kattalik va faza burchagi bo'yicha kompleks sonni
yaratadi. real = kattalik * kosinus (faza burchagi)
imag = kattalik * sinus (faza burchagi)
DASTURLASH 2
9

10. Complex sonlar uchun quyidagi operatorlar qayta yuklangan:

operator!=
operator*
operator+
operator-
operator/
operator<<
operator==
operator>>
Haqiqiy va xayoliy qismlar uchun turlarning pastki qismiga tegishli bo'lishi mumkin
bo'lgan ikkita yoki murakkab ikkala murakkab sonlar o'rtasidagi tengsizlik uchun
testlar.
Haqiqiy va xayoliy qismlar uchun turlarning pastki qismiga tegishli bo'lishi mumkin
bo'lgan ikkita murakkab raqamni ko'paytiradi.
Haqiqiy va xayoliy qismlar uchun tipning pastki qismiga tegishli bo'lishi mumkin
bo'lgan ikkita murakkab sonni qo'shadi.
Haqiqiy va xayoliy qismlar uchun tipning pastki qismiga tegishli bo'lishi mumkin
bo'lgan ikkita murakkab raqamni ayiradi.
Haqiqiy va xayoliy qismlar uchun turlarning pastki qismiga tegishli bo'lishi mumkin
bo'lgan ikkita murakkab raqamni bo’ladi.
Chiqish oqimiga murakkab raqamni kiritadigan shablon funktsiyasi.
Haqiqiy va xayoliy qismlar uchun turlarning pastki qismiga tegishli bo'lishi mumkin
bo'lgan ikkita yoki murakkab ikkala murakkab sonlar o'rtasidagi tenglik uchun testlar.
Kirish oqimidan murakkab qiymatni chiqaradigan shablon funktsiyasi.
DASTURLASH 2
10

11. Complex sonlar uchun quyidagi sinflar yaratilgan:

complex<double>
complex<float>
complex<long
double>
complex
DASTURLASH 2
Aniq ixtisoslashtirilgan sinf shablonlari ikkitomonlama tipdagi
buyurtma qilingan juftlikni saqlaydigan ob'ektni tasvirlaydi, bu erda
birinchisi murakkab sonning haqiqiy qismini, ikkinchisi esa xayoliy
qismni anglatadi.
Shubhasiz ixtisoslashtirilgan sinf shablonlari buyurtma qilingan
juftlikni saqlaydigan ob'ektni tavsiflaydi, har ikkala turdagi float ham,
birinchisi murakkab sonning haqiqiy qismini, ikkinchisi esa xayoliy
qismni anglatadi.
Aniq ixtisoslashtirilgan shablon shablonni buyurtma qilingan juftlikni
saqlaydigan ob'ektni tavsiflaydi, har ikkala turdagi uzun juft juftlik, bu
erda murakkab raqamning haqiqiy qismi, ikkinchisi xayoliy qism
tasvirlangan.
Sinf shablonlari murakkab sonlar tizimini ifodalash va murakkab
arifmetik amallarni bajarish uchun ishlatiladigan ob'ektni tavsiflaydi.
11

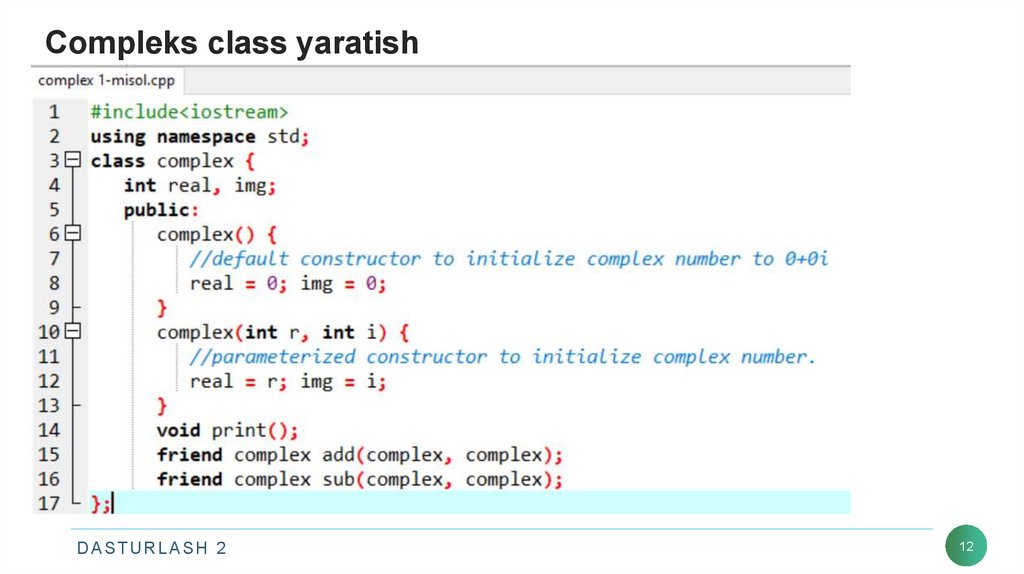
12. Compleks class yaratish

DASTURLASH 2
12

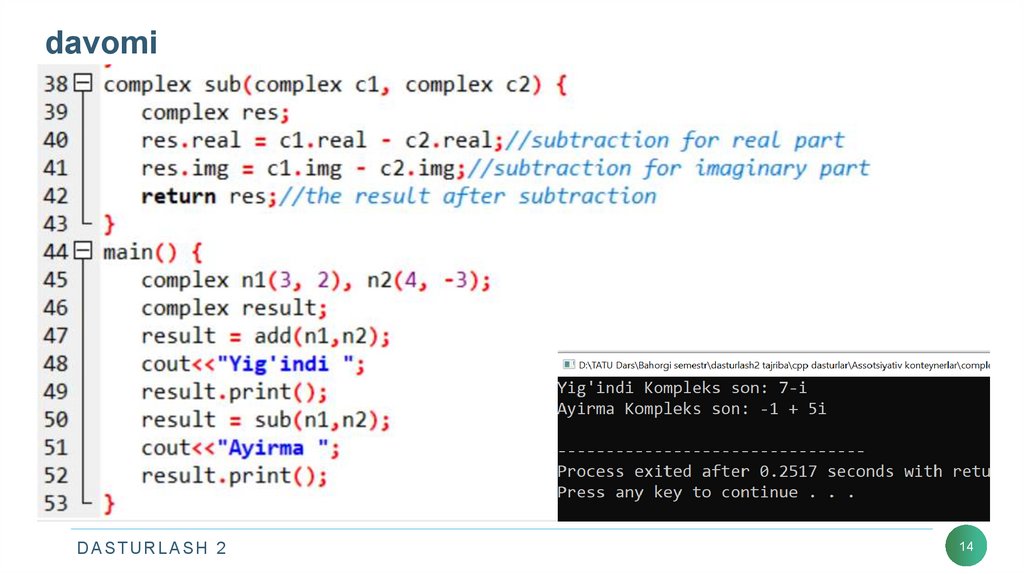
13. davomi

DASTURLASH 2
13

14. davomi

DASTURLASH 2
14

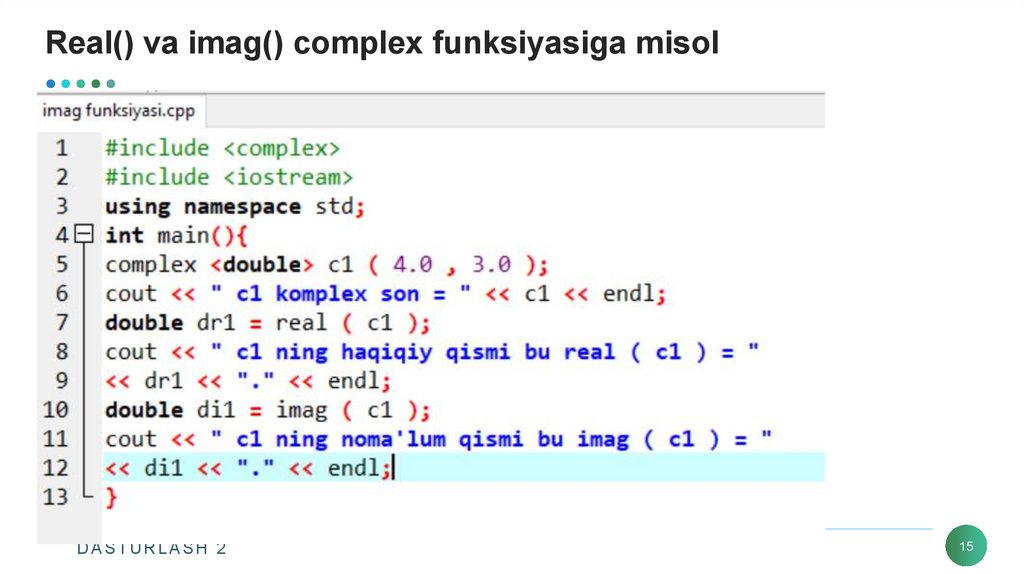
15. Real() va imag() complex funksiyasiga misol

DASTURLASH 2
15

16. Natija:

DASTURLASH 2
16

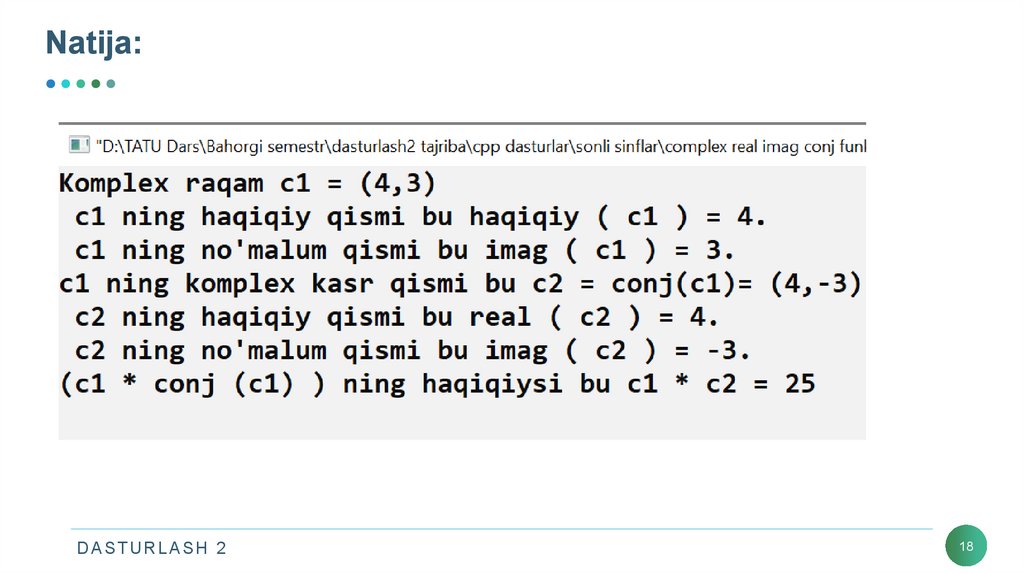
17. Complex sonli sinfga misol. real , imag, conj funksiyalarining qo’llanilishi

DASTURLASH 2
17

18. Natija:

DASTURLASH 2
18

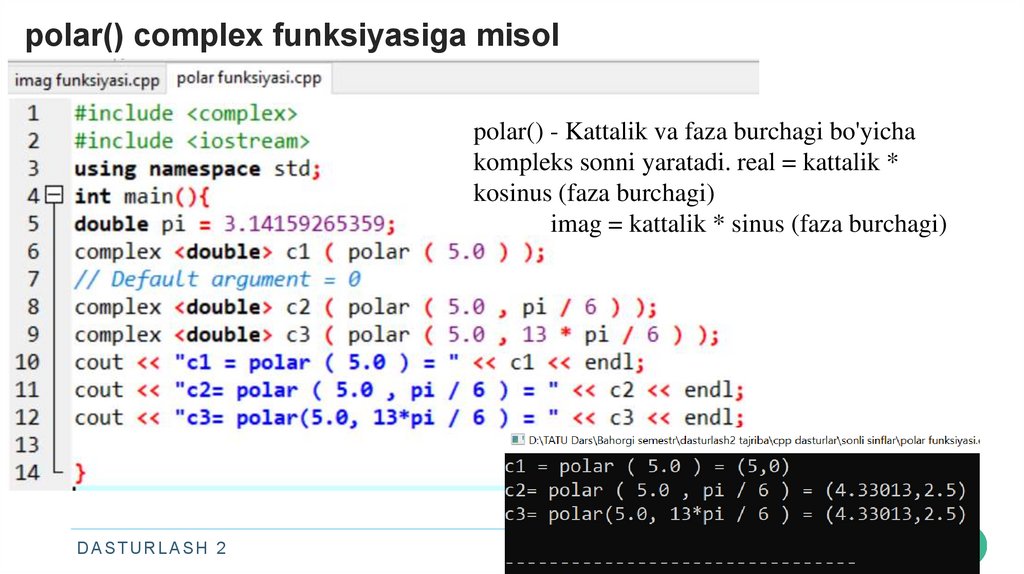
19. polar() complex funksiyasiga misol

polar() - Kattalik va faza burchagi bo'yicha
kompleks sonni yaratadi. real = kattalik *
kosinus (faza burchagi)
imag = kattalik * sinus (faza burchagi)
DASTURLASH 2
19

20. Valarray son sinfi va uning funksiyalari.

Yaqin vaqtlarda C++ da massiv elementlari bilan ishlash va
samarali saqlash uchun Valarray konteyneri yaratildi. Bu
hamma C++ standartlarida bo‘lmasligi ham mumkin.
- Bu sinf massiv element indekslari bo‘yicha birlashtirish
operatorlari va elementlararo matematik amallarni bajaradi.
- Vektor bilan solishtirganda Valarray sinf matematik amallarni
bajarishda samaraliroq hisoblanadi.
DASTURLASH 2
20

21.

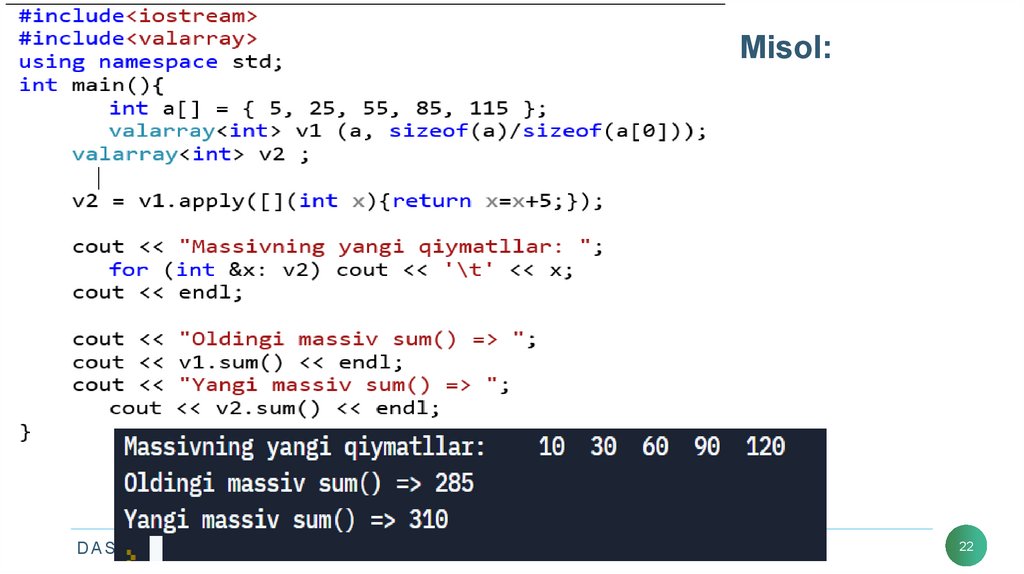
Valarray sinfning ochiq funksiyalari:
apply() – bu massiv elementlari bo‘yicha bir vaqtda
o‘zgarishlarni bajaradi va yangi massiv qaytaradi.
sum() – massivdagi elementlar yig‘indisini
qaytaradi.
DASTURLASH 2
21

22. Misol:

DASTURLASH 2
22

23.

min() va max() fnuktsiyalari mos ravishda massiv eng kichik
va eng katta elementlari qimatlarini qaytaradi.
cout << "min() => ";
cout << v1.min() << endl;
cout << "max() => ";
cout << v1.max() << endl;
shift() – berilgan son qiymat bo‘yicha indeks asosida massivni surib yangi
massiv qaytaradi. Agar son musbat bo‘lsa chapga suriladi, manfiy bo‘lsa,
o‘nga suriladi.
cshift() - berilgan son qiymat bo‘yicha indeks asosida massivni aylana
shaklida surib yangi massiv qaytaradi. Agar son musbat bo‘lsa chapga
suriladi, manfiy bo‘lsa, o‘nga suriladi.
DASTURLASH 2
23

24.

DASTURLASH 2
24

25.

swap () - bir massivni ikkinchi bir massivga almashtiradi.
varr.swap(varr1);
Yuqoridagilardan tashqari quyidagi funksiyalari mavjud:
operator= Massiv qiymatini o‘zlashtirish
operator[] Massiv indeksi orqali elementiga murojaat
resize
Massiv elemmentlar soni (hajmi) ni qayta aniqlash
size
Massiv elemmentlar soni (hajmi)
DASTURLASH 2
25

26. Slice sinfi

Valarray slice sinfi: Bu sinf valarray slice sinfini
ifodalaydi. U hech qanday elementni o'z ichiga olmaydi va unga
ishora qilmaydi - u faqat valarray::operator[] da indeks sifatida
ishlatiladigan elementlar tanlovini tavsiflaydi.
std::slice - bu std::valarray kichik to'plamini aniqlaydigan
sonli sinfi. std::slice tipidagi ob'ekt uchta qiymatga ega:
boshlang'ich indeks, qadam va kichik to'plamdagi qiymatlarning
umumiy soni. std::slice tipidagi obyektlar valarray operatori[]
yordamida indeks sifatida ishlatilishi mumkin.
DASTURLASH 2
26

27. Slice sinfi

Oddiy qilib aytganda, u indeks asosida kesish uchun ishlatiladi.
Valarray slice boshlang'ich indeks, o'lcham va qadam bilan
belgilanadi.
slice( std::size_t start, std::size_t size, std::size_t qadam );size_t
star : tanlovdagi birinchi elementning indeksidir size_t size:
tanlovdagi elementlar soniqadam : tanlangan elementlarni
ajratuvchi oraliq.
DASTURLASH 2
27

28. Slice sinfi

DASTURLASH 2
28

29. Slice funksiyasiga namuna

DASTURLASH 2
29

30. Xulosa

DASTURLASH 2
30

31.

E’tiboringiz uchun
rahmat
Savollar ?
DASTURLASH 2
31