Arifmetik amallarni o’rgatishning umumiy masalalari. Kurs loyihasi

1.

Turan Internatinal University
Gumanitar fanlar va pedagogika
fakulteti Boshlang‘ich ta’lim yo‘nalishi
SBT-22-10 guruhi talabalarining
“Arifmetik amallarni o’rgatishning umumiy masalalari.”
mavzusida tayyorlagan
KURS LOYIHASI
Tayyorladilar: Xudayberganova Nasiba
Kurs loyihasi rahbari:
Ma’suma Zokirova

2.

MUNDARIJA
• KIRISH
I. Boshlang`ich sinflarda arifmetik amallarni bajarish metodikasi.
1.1. Boshlang’ich sinflarda arifmetik amallar bajarish metodikasining umumiy
masalalari.
1.2. Arifmetik amallarni o’rgatishda amallar bajarish metodikasining umumiy
masalalari.
II. Arifmetik amallar ustida olib boriladigan ishlar.
2.1. Nomanfiy butun sonlar ustida arifmetik amallarni o’rgatish metodikasi
2.2. Yozma va og’zaki hisoblashda pedagogik texnologiyadan foydalanish.
• XULOSA
• FOYDALANILGAN ADABIYOTLAR

3.

Kirish
Boshlang’ich sinflarda arifmetik masalaning ahamiyati, mohiyati to’g’risida ko’p
gapirilgan:
a) arifmetik masala o’quvchilarga arifmetik amallarning ma’nosini chuqur
tushuntirishga,amallar xossalarining mohiyatiga to’la yetishiga ko’maklashadi;
b) o’quvchilar tafakkurini hayotiy faktlar bilan boyitadi, chunki masalada hayotiy
haqiqat aks ettiriladi;
c) o’quvchilarda matematik tilni shakllantiradi. O’quvchi istalgan matematik ifoda,
topshiriq,matnga qarab uning talabini sharhlab bera oladigan bo’ladi;
d) o’quvchida mantiqiy tafakkur rivojlantiriladi;
e) istalgan masala tarbiyaviy ahamiyatga ega. U hayot taraqqiyoti dinamikasini ochib
beradi;
f) masala yechish jarayonida o’quvchilarda fanga nisbatan qiziquvchanlik mustaqillik
vaerkin fikrlash uyg’onadi;
g) istalgan arifmetik masala nazariya bilan amaliyotini bog’lash borasidagi asosiy
vositadir;
h) masala yechish jarayonida o’quvchilarda ijodiy fikrlash shaklanadi, hayotiy
voqelikni tassavvur qila oladi;

4.

Yuqorida qayd etilganlarning boshlang’ich sinflar uchun ahamiyatini
to’ldirib, arifmetikmasala deganda shunday savolni tushunmoq kerakki,
masala shartida berilgan sonni faktlar ustida arifmetik amallar bajarilib
undagi noma’lum topiladi, deb ta’rif berish mumkin. Masala savoliga javob
uni yechib topiladi. Yechish deganda masalada berilganlar bilan
izlanayotgan miqdoro’rtasidagi bog’liqlikni aniqlash tushuniladi.
Shu munosabat bilan istalgan arifmetik masalani uch qismga bo’lish
mumkin:
1. Masalaning sharti bilan.
2. Undagi sonli faktlar.
3. Masalaning savoli
Yuqorida keltirilgan barcha argumentlar boshlang’ich sinfda matematika
o’qitishda o’qituvchi, arifmetik masalalar yechishga jiddiy e’tibor bilan
qarashi kerakligini va maktabda butun matematika kursini o’zlashtirish ishi
arifmetik masalalarga qaratilib ko’rilishi zarurligini ko’rsatadi.
Shunday savol tug’iladi, arifmetik masala bilan misol o’rtasida qanday farq
bor?

5.

Misol bu sonli ifoda bo’lib, unda amallar va ularning bajarilish tartibi amal
belgilari orqali berilgan bo’ladi. Ammo har qanday sharti, sonli faktlari va savoli
bo’lgan matn masala bo’la olmaydi. Bunda ham o’ziga xos talablar mavjud. Masala
o’z mazmuni bilan o’quvchilarga yaqin va tanish bo’lib, u o’quvchini o’rab olgan
hayot voqealarini o’zida aks ettirishi kerak. Tuzilishi jihatdan oddiy, tushunarli, iloji
boricha qisqa matnli bo’lishi kerak. Sonli faktlar hayotiy, real, imkoniyat
chegaramizga sig’adigan, mantiqan to’g’ri tanlanganva taraqqiyot dinamikasini
ochib beradigan bo’lishi kerak.
Boshlang’ich sinf darsliklarini tahlil qilganimizda 1-sinfdan boshlab, har bir darsda
hech bo’lmaganda bir yoki bir necha masalaga duch kelamiz. Masalalarni
o’quvchilrga tushuntira olish o’qituvchining mahoratiga bog’liq bo’ladi. O’qituvchi
esa kuchli bilim va metodik mahoratga ega bo’lgan, bolalarni chin dildan sevuvchi
inson bo’lishi kerak.
Masala tuzish ishi boshlang’ich sinf o’quvchilari uchun ancha murakkabligini
unutmaslik kerak. Chunki bolalar masala tuzayotganda kerak bo’lgan miqdorlar
sonini, ularni bir-biriga bog’lashni hali yaxshi bilishmaydi. Masalaga savol
qo’yishda qiynalishadi.

6.

Shuning uchun avval o’qituvchining o’zi masalaning qanday yuzaga kelishini
amaliy tarzida tuzib ko’rsatadi.
Masalan, 1 sinfda noma’lum qo’shiluvchini topishga doir masala “Stolda 29 ta
daftar yotibdi. 12 tasi katakli daftar, qolganlari esa bir chiziqli daftar. Nechta
daftar bir chiziqli?” yechilsa, unda o’quvchilar ko’z o’ngida shunga o’xshash
quyidagicha masalani tuzib ko’rsatish mumkin.
O’qituvchi stoliga bir qancha daftar qo’yadi. Bir o’quvchiga shu daftarlar ustiga
yana ikkita daftar qo’shishni aytadi. So’ngra hamma daftarlar sanaladi va oldin
stol ustida nechta daftar bo’lganligini aniqlash maqsadida masala tuziladi va
yechiladi. Yoki noma’lum kamayuvchini topishga doir masala “Zarinada bir nechta
daftar bor edi. U o’rtog’iga ikkita daftarini berganidan keyin uning 9 ta daftari
qoldi. Zarinada nechta daftar bo’lgan?” yechilgach, noma’lum ayriluvchini
topishga doir “Do’konda 100 dona changyutgich bor edi. Bir nechta changyutgich
sotilgan keyin 91 ta changyutgich qoldi. Nechta changyutgich sotib yuborilgan?”
Keyinchalik rangli rasmlar yuzasidan masalalar tuzish, tuzdirish orqali bu kabi
ijodiy ishlar kengayib boradi. Masala tuzish uchun rasmlarda berilgan ma’lumotlar
o’quvchilarga ancha tanish bo’lib, bunda o’quvchilarning asosiy vazifasi rasmini
”o’qib” unga savol qo’yishdan iborat bo’ladi.

7.

DOLZARBLIGI
Bo'lajak boshlang'ich sinf o'qituvchilarining kichik yoshdagi maktab
o'quvchilariga matematikani o'qitishda amaliyotda yuzaga keladigan turlicha
ijtimoiy-iqtisodiy, bozor iqtisodiyotiga oid, o'quvchilarni ijodiy faollikka
yetaklaydigan, metodik vazifalarini mustaqil hal etish uchun tayyorgarlik
saviyalarini oshirishni nazarda tutadi. Ularni hayotga tadbiq etish ishlari
davlat siyosatining ustivor yo'nalishlaridan biri deb hisoblanayotgan bugungi
kunda xalq ta'limi sohasidagi muammolarni va ularni vujudga keltiruvchi
omillarni aniqlash hamda ularni chuqur ilmiy tahlil qilish zarur bo'ladi.
Kadrlar tayyorlash milliy dasturini amalga oshirishda eng avvalo
boshlang'ich ta`lim tizimini to'g'ri yo'lga qo'yish muhim ahamiyatga ega.
Ma`lumki, ta`lim sifati va samaradorligi ko'p jihatdan ta`lim mazmunini to'g'ri
tanlanishiga bog'liq.
1-4 sinflardagi matematika darslari umumiy o'rta ta`lim maktab matematika
fani uchun asos, poydevor ekan, bu sinflarda matematika fani o'qitilishi eng
zamonaviy talablar darajasiga ko'tarmoq zamon talabidir, chunki bolalarga
keyinchalik matematika va boshqa fanlar uchun zarur bo'lgan elementar,
tushunchalar shu sinflarda singdiriladi.

8.

Matematika fanini o`qitishda masalalar yechish juda muhim o`rin tutadi, chunki
masala yechishda maqsad-o`quvchilarning nazariy biliblarini har hil amaliy
masalalarni yechish sohasida ongli ravishda tez va qat`iylik bilan tadbiq
qilishga o`rgatishdir.
Masala yechish – matematik nazariyani amaliyotda tadbiq qilishdan iboratdir.
Matematika o`qitishda masala yechishning pedagogik mohiyati naqadar katta
ekanligi va o`qituvchi o`z ishini rejalashtirishda ham, o`qitish vaqtida ham
bunga qanchalik e`tabor berish kerakligi shu aytilganlardan ham yaxshi
tushuniladi. Masalalar yechish yo`li bilan har-xil matematik tushunchalar
vujudga keltiriladi, turli arifmetik operatsiyalar tushunib olinadi, masalalr
ko`pincha ba`zi nazariy qoidalarni chiqarishda asos bo`ladi. Masala
o`qituvchining matematik nutqini boyitishga va o`stirishga yordam beradi.
Masalalar hayotdagi turli faktlar orasidagi miqdoriy munosabatlarni anglashga
yordam beradi. Tegishli mazmundagi masalalar o`quvchilarni vatanparvarlik
ruhida tarbiyalashda vosita bo`ladi. O`quvchilarning mantiqiy fikrlashining
o`sishida, ularning miqdorlar orasidagi bog`lanishlarni aniqlashida, tog`ri
hulosalar chiqara bilishda masalalar ayniqsa muhim o`rin tutadi.

9.

Kurs loyihasi metodlari
“Adashgan zanjirlar”
Tavsifi: Boshlang’ich sinflarda biror bir ketma – ketlikni tiklash uchun qo’llanadi. Bunda o’qituvchi
biror mavzu, tushunchaga oid ketma – ketlikni alohida – alohida va tartibsiz qo’yadi. O’quvchilar
tartibsiz joylashgan so’zlarga mantiqiy bog’langan zanjirni tuzishlari kerak.
Qo’llanilishi: Bu metodni 4-6 kishilik guruhda qo’llash ham, butun sinf bilan ishlash ham mumkin.
O’qituvchi bilim uzatuvchi rolidan o’quv jarayonini tashkil qiluvchi, o’qish faoliyatini boshqaruvchi,
o’quvchilar faolligini psixologik va pedagogik jihatdan oqilona qo’llab quvvatlab rivojlantiruvchi roliga
o’tishi, deb hisoblaymiz.
Foydasi: Pedagogik texnologiya nazariyasi va uni ta’lim jarayonida qo’llash muammolariga
bag’ishlangan zamonaviy tadqiqotlar mazkur nazariyaning ta’lim rivojini ta’minlashdagi ahamiyatini
chuqur anglab yetish, uning imkoniyatlarini aniqlash va keng ko’lamli axborot maydonini egallashga
yordam beradi.
Pedagogik texnologiya nazariyasini shakllantirish va undan foydalanish mexanizmini bilish, ta’lim
jarayonini rivojlantirish va boshqarishning eng samarali shakl va metodlarini aniklash imkonini beradiki,
buning nafaqat nazariy, balki amaliy ahamiyati ham beqiyosdir.
Ta’lim nazariyasi va amaliyotida pedagogik texnologiyalarni tadqiq etish ishi fanlararo
(pedagogika, psixologiya, metodologiya, pedagogik metodologiya, falsafa, sotsiologiya va boshqa
fanlar) aloqadorlik va bog’liqlik asosida yondashuvni talab etadi.

10.

Interfaol metod sinfda o’tiladigan mavzular yuzasidan muammoli
vaziyatlarni muhokama qilishda “Aqliy hujum”, “Adashgan zanjirlar”,
“Savol bering”, “Insert”, ”BBB”, “Bahs – munozara”, “Muammoli
savollar”, “Kichik guruhlarda ishlash”, “Burchaklar metodi“, “Kubiklar”
metodlari asosida bahs, munozara orqali ularni yechimini topishda
yaqindan yordam beradi.
“Aqliy hujum” texnologiyasini qo’llash bir muammoni hal qilish yo’lidan
turlicha va iloji boricha ko’proq taklif, fikr – mulohazalarni yig’ishdan
iborat. Avvaliga har qanday takliflar qabul qilinadi. Keyin esa, ularning
ichidan eng ma’qulini tanlab olinadi. Bu metodni qo’llashda eng nozik
tomoni hamma takliflarni “Eslab” qolishdir. Shuning uchun ularni yozib
borish kerak bo’ladi. O’qituvchi ularni shartli belgilar va qisqartirishlar
bilan doska yoki vatman qog’ozga yozib boradi.

11.

I. Boshlang`ich sinflarda arifmetik amallarni bajarish metodikasi.
1.1. Boshlang’ich sinflarda arifmetik amallar bajarish metodikasining umumiy
masalalari.
Davlat ta'lim standard o'quvchilarning har biriga ta'lim olishda teng
imkoniyatlarni yaratib berish,har birining yuqori natijaga erishishlarini
rag'badlantirish va shu orqali o'quv- bilim jarayoning farqli tashkil etilishini
ta'minlash uchun da'vat etilga. Davlat ta'lim standarlarining o'quv fani
bo'yicha, ta'lim sohalari bo'yicha ishlab chiqarilishi o'quv fanlarining
variantini tanlash asosida o'quv metodik majmualar, jumladan, boshlang'ich
sinflarda matematika o'qitishni takomilashtirishni nazarda tutadi.
Boshlang'ich sinflarda arifmetik amallar bajarishni bog'lanish va bilimlarni
muvofiqlashtirish tamoyili asosida o'quv fanlarining ichki bog'liqligi va
o'quv fanlari aro uzviylikni ta'minlashga xizmat qiladi. Boshlang'ich
sinflarda arifmetik amallar bajarish talablarining o'quvchilar tomonidan
bajarilishi ularning tevarak zarur bilim, malaka va ko’nikmalarni
egallashlariga yordam beradi.

12.

a) o'quvchilarning tevarak atrofdagi tabiiy muhitga moslashtirish.
b) faoliyatning har-xil turlarini o'quv mehnat, muloqatni egallash.
c) o'z-o'zini nazorat qilish hamda baholashga o'rgatish.
d) muayyam umumiy tabiiy-ilmiy iqtidorning belgilangan darajasi uning keyingi
taraqiyotining tavsifi.
Shunday qilib, boshlang'ich sinflarda arifmetik amallar bajarish jarayoni o'quvbilim jarayoniga matematika o'qitish bo'yicha bilim,konikma va malakalarigina
emas balki shaxsning muayyam asosiy faoliyati majmuasi- mehnat o'quv-biluv,
kammunikativ-axloqiy va jismoniy- kamolatiga mos keladigan fazilatlarining
shakllanishini ham taminlaydi.
O’quvchilarning arifmetik amallarni bajarishga o'rgatish metodikasining nazariy
asoslari. Tizimda yuz berayotgan ijtimoyi - iqtisodiy munosabatlar, xalq ta'limi
tizimida bo'layotgan o'zgarishlar "Ta'lim taraqqiyoti qonunda ham" Kadrlar
tayyorlash Milliy dasturi " da ko'rsatib o'tilgandek, har bir sinf o'quvchisiga
oldiga muhim vazifa qo'yilmoqda. Bu vazifalar boshlang'ch ta'lim uchun ham xos
bo'g'inlarni ajratish imkonini beradiki, bu bo'g'inlar xilma -xil o'quv fanlari
dasturlarida, o'quv rejalarida, darsliklarda ta'limning joriy etilishi hamda metodik
tizimida biror tarmoqni hosil qilish mumkin.

13.

O'quvchilarni matematikadagi arifmetik amallarni bajarishga
o'rgatish metodikasi. Bu mavzu ustida ishlashda o'qituvchi oldida
turgan asosiy maqsadlar quydagilardan iborat:
1. O'quvchilarni qo'shish va ayirish, ko'paytirish va bo'lish amallarining
mazmuni bilan tanishtirish;
2. Hisoblash usullaridan o'quvchilarni o'nlik foydalanishlarini
ta'minlash;
a) Sonni qismlari bo'yicha qo'shish va ayirish usuli.
b) Yig'indining o'rin almashtirish xossalaridan foydalanish qo'shish
usuli.
c) Sonlarni ayirishda qo'shishning tegishli holini bilishdan yoki yig'indi
va qo'shiluvchilardan biri bo'yicha ikkinchi qo'shiluvchilarni topish
malakasidan foydalanadigan holda yig'indi bilan qo'shiluvchilar
orasida bog'lanishlarni bilganlikda asoslanib ayirish usuli.
d) Qo'shish va ayirish, ko'paytirish va bo'lish ko'nikma, malakalarni
shakllantirish.

14.

Qo'shish va ayirishni o'rganish ishini o'zaro bog'langan bir nechta bosqichga
bo'lish mumkin. O'quvchilarda og'zaki va yozma ko'nikmalarni tarkib toptirish
matematika dasturining asosiy yo'nalishlardan biridir. Arifmetik amallarni
o'rganishdan oldin bolalar ongiga uning ma'nosini, mazmunini yetkazish kerak. Bu
vazifa turli xil amaliy ishlarni bajarish asosida o'tkaziladi.
U: "o'nlik" mavzusini qo'shish va ayirish amallarning ma'nosi ikki to'plam
elementlarini birlashtirish va to'plamdan uning qismlarini ajratish kabi amallar
yordamida olib boriladi. Ko'paytirishni uning komponentlari bilan natijasi orasidagi
bog'lanishlarni o'rganish asos bo'lib hizmat qiladi. Demak, o'qitishning 1bosqichida abstrakt bo'lgan narsa navbatdagi bosqichda yanada abstraktroq
bilimlarni shakllantirish uchun aniq asos bo'lib hizmat qiladi.
Turli hisoblash usullarining o'zlashtirilishi uchun dasturda arifmetik amallarning
ba'zi muhim xossalari va ulardan kelib chiqadigan natijalar bilan tanishtirishni
nazarda tutadi.
Dasturda arifmetik amallarning xossalarini o'rganishdan tashqari arifmetik amal
hadlari va natijalari orasidagi bog'lanishlarni ham ko'zda tutadi. Bu ish amallarni,
tenglamalarni tekshirishda muhim ahamiyatga ega.
Masalan: 6x4=24 bo'lsa, uni bo'lishga bog'lab 24:6=4; 24:4=6 kabi hadlar hosil
qilinadi.

15.

1.2. Arifmetik amallarni o’rgatishda amallar bajarish metodikasining
umumiy masalalari.
Muhim vazifalaridan biri hisoblash ko'nikmalarni shakllantirishdir. Og'zaki va yozma usulda
hisoblashlar sinflarning har bir mavzusida o'z aksini topgan. Masalan: og'zaki
276 + 432 = (200+400) + (70+30) + (6+2) = 600+1008 =708
Yozma: Og'zaki hisoblashlarning asosiy ko'nikmalari 1 va 2- sinflarda shakllanadi. Og'zaki
hisoblash usullari ham, yozma hisoblash usullari ham amallar xossalari va ulardan kelib chiqadigan
natijalarni amallar kompanentlari bilan natijalari orasidagi bog'lanishlarni bilganlikka
asoslanadi.Yangi boshlang’ich matematika kursida, avvaldagiga o’xshash, arifmetika asosiy o’rinni
egallaydi.
1-4- sinflarning yangi dasturida arifmetik material mazmuni unchalik ko’p o’zgarmagan:
a) arifmetika nazariyasi (amallarning xossalari, natijalar va komponentlar orasidagi o’zaro
bog’lanish, komponentlardan biri o’zgarganda;
b) amallar natijalarining o’zgarishi) kamroq yoritilgan, nazariyaning amaliy masalalar (sanoq,
o’lchashlar, hisoblashlar, masalalar yechish) bilan bog’lanishi yanada mustahkamlangan:
c) eng muhim tushunchalar (son, sanoq sistemasi, arifmetik amallar)ni shakllantirishning bir muncha
mukammal sistemasi ko’zda tutilgan.
Shuningdek, arifmetikani boshlang’ich o’rganish uslubi ham mukammallashtirilgan.

16.

• Har bir sonning tarkibi o`rganiladi.
• 10 sonining tarkibi bu- 9 bilan 1, 8 bilan 2, 7 bilan 3, 6 bilan 4, 5 bilan 5 ning
yig`indisidan hosil bo`lishi aytib o`tiladi.So’ng nol soni mavjud emas ma`nosini
bildirishi eslatib o`tiladi.
• So`ng 1 sonini qo`shish turli xil ko`rgazmalar yordamida tushuntiriladi.
• Menda 8 ta daftar bor edi, yana 1 ta daftar sotib oldim. Mendagi daftarlar soni
nechta? 8+1=9
• Likopchada 5 ta olma bor sdi. Onam yana 1 ta olmani likopchaga qo`ydi.
• Likopchadagi olmalar soni nechta bo`ldi? 5+1=6
• Ko`lmakchada 4 ta go`zlar suzib yurgan edi. Ularga ya 1 ta g`oz kelib qo`shildi.
Go`zlar nechta bo`ldi? 4+1=5 So`ng ayirishga oid bo`lgan tushunchalar
ko`rgazmalar yordamida tushuntiriladi.
• Shoxda 7 ta olma bor edi. 1 ta olma uzilib tushdi. Shoxda nechta olma qoldi? 7-1=6
• Onam 4 ta yopilgan nonni dasturxonga qo`ydi. 1 ta non yeyildi. Dasturxonda nechta
non qoldi? 4-1=3 Simyog`ochda 5 ta qaldirg`och bor edi. 1 ta qaldirg`och uchib
ketdi.
• Simyog`ochda nechta qaldirg`och qoldi? 5-1=4

17.

• O‘nlik konsentrida o‘rganiladigan matematik tushunchalar.
O‘quv dasturida 1-sinfda “1 dan 10 gacha bo‘lgan sonlar” hamda “10 ichida qo‘shish va
ayirish” bo‘limlarini o‘rganishda quyidagi matematik tushunchalarni o‘quvchida shakllantirish
nazarda tutiladi:
Qo‘shishning asosiy xossasi.
Qo‘shishda 0 ning xossasi.
Ayirishning xossasi.
Ayirishda 0 xossasi.
Qo‘shish amalining tarkibiy qismlari (birinchi qo‘shiluvchi, ikkinchi qo‘shiluvchi, yig‘indi) va ayirish
amalining tarkibiy qismlari (kamayuvchi, ayriluvchi, ayirma).
Qo‘shish bilan ayirish orasidagi munosabat.
Qo‘shishning o‘rin almashtirish xossasi.
Hisoblash usullari: bo‘laklab qo‘shish usuli, sonlarning o‘rinlarini almashtirish;
bo‘laklab ayirish va ayirish bilan qo‘shish orasida bog‘linishga asoslangan ayirish usuli.
Bir xonali songa 0, 1, 2, 3, 4 ni qo‘shish (10 ichida).
Bir xonali songa 5, 6, 7, 8, 9 ni qo‘shish (10 ichida).
0, 1, 2, 3, 4 ni ayirish (10 ichida).
5 ,6, 7, 8, 9 ni ayirish (10 ichida).
10 ichida qo‘shish jadvali, xuddi shunday ayirish amali uchun.
Quyidagi ko‘rinishdagi ayirish va qo‘shishni bajarish: 9 – 9, 0 + 5, 7 – 0, 8 + 0.

18.

• 1 va 2 amalli sonli ifodalarni o‘qish, yozish va qiymatini topish (qavssiz misollar).
• Berilgan sondan bir necha birlik katta yoki kichik bo‘lgan sonni topish.
• Yig‘indini, qoldiqni, noma’lum qo‘shiluvchilarni topish, sonni bir necha birlik orttirish
(kamaytirish) va taqqoslashga oid (amaliy ish va rasmlar, qisqa yozuv bo‘yicha, to‘liq
bo‘lmagan narsalar ko‘rgazmasi asosida) sodda arifmetik masalalarni yechish.
• Arifmetik amallarni qo‘shish va ayirishga doir matnli masalalarni yechish.
Birinchi yarim yillikda o‘quvchilar matematik amallar nomlari, tarkibiy qismlari, ular hosil
etadigan natijalar nomlari bilan tanishadilar. Bundan tashqari o‘quvchilar matematik
belgilarning ba’zi elementlari amal ishoralari (plyus − qo‘shish, minus − ayirish),
munosabat belgilari (katta, kichik, teng) bilan tanishishlari hamda 2 + 6 (2 va 6 sonlari
yig‘indisi), 9 – 2 (9 va 2 sonlari ayirmasi) va boshqa shunga o‘xshash eng sodda
matematik ifodalarni o‘qish va yozishni o‘rganib olishlari kerak.
• 3 + 3 va 7 + 3, 6 + 3 va 6 – 3 ko‘rinishdagi ifodalarni taqqoslashga doir mashqlarni
bajarishda bolalar bu ifodalar orasidagi o‘xshash va farqli xususiyatlarni ko‘radilar va
shu asosda ularning qiymatlari teng yoki teng emasligi, agar teng bo‘lmasa, u holda
berilgan ifodalardan qaysinisining qiymati katta (kichik) degan savollarni hal qiladilar.
Chiqarilgan xulosa har doim asoslanishi, so‘ngra hisoblashlar yordamida tekshirilishi
kerak.

19.

Shuni ta’kidlash joizki, o‘quvchilarni 10 ichidagi sonlar tarkibini puxta bilishi sondan 5,
6, 7, 8, 9 ni ayirishni tez o‘rganishga olib keladi. Masalan, 8 – 5 ayirma javobi 3 bo‘ladi,
chunki 8 – bu 5 va 3 ning yig‘indisidan iborat: 8 = 5 + 3, demak, 8 – 5 = 3.
Bunga juda ko‘plab mashqlar bajarish natijasida erishish mumkin.
1. 10 sonini hosil qilish. O‘ndan sonni ayirish.
2. Qo‘shish va ayirishning o‘zaro bog‘liqligi. Qo‘shish va ayirish jadvali.
Ayirishni qo‘shish asоsida bajarishda o‘quvchilarga yig‘indi va qo‘shiluvchilar o‘zarо
qanday bоg‘langanini ko‘rsatish kеrak. Bunday kuzatishlar o‘quvchilarda quyidagi
mashqlarni bajarish jarayonida qo‘shish va ayirish ustida ishlashning bоshidan
bоshlabоq yig‘ila bоradi: bеrilgan rasm (ruchka va kitоb) asоsida qo‘shish va ayirishga
dоir misоllar tuzing, хuddi shunga o‘хshash bеrilgan rasm bo‘yicha qo‘shish va
ayirishga dоir masalalar tuzing. (Masalan, o‘tlоqda 3 ta оq va 1 ta qоra echki
o‘tlamоqda, hammasi bo‘lib nеchta echki o‘tlamоqda? O‘tlоqda 4 ta echki: bitta qоra,
qоlgani оq echkilar nеchta? va hоkazо).
O‘quvchilar quyidagi misоllar juftlarini tuzadilar va yеchadilar, shuningdеk, ularni
tahlil qiladilar: 4 + 36 +4 2 + 77 – 310 – 49– 2 O‘quvchilar qo‘shish va ayirishning o‘zarо
bоg‘lanishinio‘zlashtirib оlganlaridan so‘ng ayirishning ayriluvchi to‘rtdan katta
bo‘lgan hоllarni o‘rganishga o‘tiladi.
Endi ayirish natijasi qo‘shishning mоs hоlidan fоydalanib tоpiladi: 9 – 6 = ? 9 bu 6 + 3; 6
ni ayiramiz, 3 hоsil bo‘ladi.

20.

Dоskada chaqirilgan bоlalar amallar qanday tartibda bajarilishi kеrakligini va nima uchun har
bir amal bеlgisi ustiga bu amal tartib bo‘yicha nеchanchi bo‘lib bajarilishini ko‘rsatuvchi
raqam qo‘shilishini tushuntiradilar. U hоlda shunday misоllarni o‘qituvchi ularga taklif etadi.
Masalan: 25 + 49 : 7 – 8
100 – 42 + 36 : 6
63 – 60 + 18* 2
38 – 7 *5 + 6
12 + 15 * 2 *3
9 *4 – 18 : 6
Ushbu qоida tеkshirib ko‘riladi: “Ifоdalarda avval tartib bilan (chapdan o‘nga) ko‘paytirish va
bo‘lish amallari, kеyin esa qo‘shish va ayirish amallari bajariladi”.
Qavsli ifоdalarda amallar bajarish tartibi haqidagi qоida ham shunga o‘хshash takrоrlanadi.
Bunda quyidagi ko‘rinishdagi misоllarni qarash fоydalidir:
( 70 – 30 ) + 27 : 9 ,
60 – ( 90 – 64 ) : 2 va hоkazо.
SHunga o‘хshash mashqlarni kоllеktiv bo‘lib (dоskada va daftarda yozib) bajargandan so‘ng
ikki juft qavsni o‘z ichiga оlgan ifоdalardagi amallar tartibi qaraladi. Masalan:
300 – ( 94 – 90 )*( 35 – 10 ) ,
12 + 2*9 – ( 34 – 16 ) + ( 80 – 20 ) va hоkazо. Quyidagicha
хulоsa chiqariladi: avval birinchi qavsdagi amal, kеyin ikkinchi qavsdagi amal bеriladi va
shundan kеyingina qоlgan amallar bajariladi.
Ikkinchi misоlning dоskadagi yozuvi quyidagi ko‘rinishga ega bo‘ladi:
12 + 2*9 – ( 34 – 16 ) + ( 80 – 20 ) =72
Navbatdagi qadamqavs ichida bir emas, ikkita amal qatnashgan qavsli ifоdalarni qarashdan
ibоrat. Masalan, 34 + ( 60 – 20 – 15 ) – ( 40 – 8 *4 )
Eng охirgi bоsqich ko‘rinishidagi misоllar yеchiladi.
987 – ( 109 + 163 *4 ) + 17 *10 + 394 =790

21.

Masala. 82 nafar о‘quvchi shaxmat va basketbol tо‘garagiga qatnashadi, 32 nafar
talaba basketbol va voleybol tо‘garagiga qatnashadilar, 78 nafar о‘quvchi shaxmat
va voleybol tо‘garagiga qatnashadi. Agar har bir о‘quvchi faqat bir sport turi bilan
shug‘ullansa, nechta о‘quvchi shaxmat, voleybol va basketbol tо‘garagiga
qatnashadi?
Yechish:
1) 82 + 32 + 78 = 192 nafar talaba shaxmat, basketbol va voleybol tо‘garagiga
qatnashayotgan о‘quvchilar sonining ikkilangani.
2) 192: 2 = 96 nafar shaxmat, basketbol va voleybol tо‘garagiga qatnashayotgan
о‘quvchilarning umumiy soni.
3) 96 - 32 = 64 nafari faqat shaxmat tо‘garagiga qatnashayotgan о‘quvchilar soni.
4) 96 -78 =18 nafari faqat basketbol tо‘garagiga qatnashayotgan о‘quvchilarlar
soni.
5) 96 -82 =14 nafari faqat voleybol tо‘garagiga qatnashayotgan о‘quvchilar soni.
Javob: 64 nafari shaxmat tо‘garagiga, 18 nafari basketbol tо‘garagiga, 14 nafari
voleybol tо‘garagiga qatnashadi.

22.

Masala. Ikkita vazada 75 dona gul bor edi. Birinchi vazada 6 ta gul ikkinchi vazadan 9 ta
gul olinsa, vazadagi gullar soni tenglashadi. Har bir vazada nechtadan gul bor.
Yechish: I bosqichga asosan masalada vazadagi gullar haqida gap boradi.
II bosqichda: masaladagi ma’lum kattaliklar qiymatlari. Jami vazadagi gullar 75 ta,
birinchi savatdan 6 ta , ikkinchisidan 9 ta gul olingan.
III bosqichda : izlanayotgan noma’lumlar: Har bir vazadagi gullar soni. Masalani
tenglashtirish usuli bilan yechamiz.
Birinchi vazadan 6 ta, ikkinchi vazadan 9 ta gul olingan bо‘lsa, jami vazalardan olingan
gullar soni 6 + 9 =15 ta bо‘ladi. Endi jami gullar sonidan olinganlari ayriladi ya’ni 75-15=60
ta gul qoldi.
Natijada ikkala vazadagi gullar soni tenglashadi va u 60:2=30 ya’ni har bir vazadagi
gullar soni 30 ta bо‘ladi.
Tekshirish: Birinchi vazada 30 gulga olingan 6 ta gulni va ikkinchi vazadagi 30 ta gulga
olingan 9 ta gulni qо‘shib jami gullar soni bilan taqqoslaymiz.
30+ 6=36
30+9=39
36+39=75 yechim tо‘g‘ri.
Javob: Har bir vazada 30 tadan gul bor

23.

2.2. Yozma va og’zaki hisoblashda pedagogik texnologiyadan foydalanish.
Interfaol metod - ta’lim jarayonida o’quvchilar hamda o’qituvchi o’rtasidadagi faollikni oshirish
orqali o’quvchilarning bilimlarni o’zlashtirishini faollashtirish, shaxsiy sifatlarini rivojlantirishga
xizmat qiladi. Interfaol metodlarni qo’llash dars samaradorligini oshirishga yordam beradi.
Interfaol ta’limning asosiy mezonlari: norasmiy bahs – munozaralar o’tkazish, o’quv materialini
erkin bayon etish va ifodalash imkoniyati,o’quvchilar tashabbus ko’rsatishlariga imkoniyatlar
yaratilishi, kichik guruh, sinf jamoasi bo’lib ishlash uchun topshiriqlar berish va boshqa
metodlardan iborat bo’lib, ular ta’lim – tarbiyaviy ishlar samaradorligini oshirishda o’ziga xos
ahamiyatga ega.
Metodni amalga oshirish tartibi:
Pedagog-trener ishtirokchilarni 5-6 kishidan iborat kichik guruhlarga ajratadi;
Treningni maqsadi,shartlari va tartibi bilan ishtirokchilarni tanishtirgach, har bir guruhga umumiy
muammoni tahlil qilinish shart bo`lgn qismlari ko`rsatilgan materiallar tarqatiladi;
Har bir guruh o`ziga berlgan muammoni atroflicha tahlil qilib o`z mulohazalarini tavsiya
etilayotgan sxema bo`yichatarqatmaga yozma bayon qiladi;
Navbatdagi bosqichda barcha guruhlar o`z taqdimotlarini o`tkazadilar.Shundan so`ng, pedagogtrener tomonidan tahlillar umumlashtiriladi, zaruriy axborot bilan to`ldiriladi, mavzu yakunlanadi.

24.

25.

26.

Endi masalalarni arifmetik usulda yechishning sxematik metodidan foydalanib masala yechimini
shakllantiramiz.
Masala. Sinovda 60 ta savol berildi, har bir tо‘g‘ri javob 5 ballga baholandi. 4 ta notо‘g‘ri javob uchun jarima
sifatida bitta tо‘g‘ri javob bekor qilindi. Bu sinovda hamma savollarni belgilagan bir о‘quvchi 225 ball olgan
bо‘lsa, u nechta tо‘g‘ri javob bergan?
Yechish: Masalani yechishni quyidagi tahlil orqali amalga oshiramiz, ya’ni birinchi bosqichda masalani
о‘qib, unda test sinovi haqida gap borayotganini aniqlashtiramiz. Ikkinchi bosqichda masalaga savollar
berish orqali masaladagi kattaliklar qiymatlari, nimalar ma’lum, nimani topish kerakligi, yechim rejasi
aniqlashtiriladi. Uchinchi bosqichda yechimni amalga oshiramiz, ya’ni izlanayotgan noma’lum topiladi.
Demak yechishni quyidagi ketma-ketlik orqali amalga oshiramiz.
1. О‘quvchi sinov natijasida 225 ball olish uchun nechta savolga javob bergan;
2. Sinovda jarimalarni hisoblamagandagi notо‘g‘ri javoblari soni;
3. 4ta notо‘g‘ri javob uchun 1 ta tо‘g‘ri javob bekor qilingan bо‘lsa, о‘quvchi aslida nechta savolga tо‘g‘ri javob
bergan.
О‘quvchi sinovda nechta savolga tо‘g‘ri javob bergan
1
2
225:5=45
60-45=15
3
Agar о‘quvchi 4ta notо‘g‘ri javob uchun 1 ta tо‘g‘ri
javob bekor qilinsa, 12 ta notо‘g‘ri javob uchun 3ta
tо‘g‘ri javob bekor qilingan. U holda 12+3=15bо‘ladi.
Natijada О‘quvchi 45+3=48 savolga tо‘g‘ri javob
bergan.

27.

II. Arifmetik amallar ustida olib boriladigan ishlar.
2.1. Nomanfiy butun sonlar ustida arifmetik amallarni o’rgatish metodikasi
Hisoblashlarning ravon va tez bo‘lishiga katta e’tibor berilishi kerak. Shu bois qo‘shish va ayirishga doir u
yoki bu misolning yechilishini mufassal tushuntirishdan o‘quvchi yo‘l qo‘ygan xatoliklarni tushuntirishda
zarur bo‘lib qolganda foydalanish kerak. Bоlalarning kuzatishlar va amallar bajarishdan chiqargan
хulоsalari taхminiy quyidagicha bo‘lishi mumkin: “Ikkita sоnni qo‘shishda ularning o‘rinlarini
almashtirish mumkin” yoki “Qo‘shayotgan sоnlarimizning o‘rinlarini almashtirishimiz mumkin”.
Bunda o‘qituvchi sоnlarning o‘rnini faqat qo‘shishda almashtirish mumkinligini, ayirishda esa bunday
qilish mumkin emasligini bоlalarning оngiga albatta yеtkazish kеrak. Buni tayin misоllarda ko‘rsatib
bеrishlari maqsadga muvofiq.
Sondan 5,6,7,8,9 sonlarini ayirish. Bu hollarda hisoblash usullari yig‘indi bilan qo‘shiluvchilar orasidagi
bog‘lanishlarni bilganlikka asoslanadi. Shu bilan birga, 10 ichidagi son tarkibiga ishlar bajarishvagrafik
tasvirlar yordamida ochib beriladi. Masalan, quyidagi rasmga qarab,tegishli bog‘lanishlarni aniqlashadi:
5 + 2 =7
7–2=5
7–5=2
Bunday mashqlarni bajarish natijasida o‘quvchilar bunday xulosaga kelishadi: agar ikki qo‘shiluvchilarning
yig‘indisidan bu qo‘shiluvchilarning biri ayrilsa, ikkinchisi hosil bo‘ladi.

28.

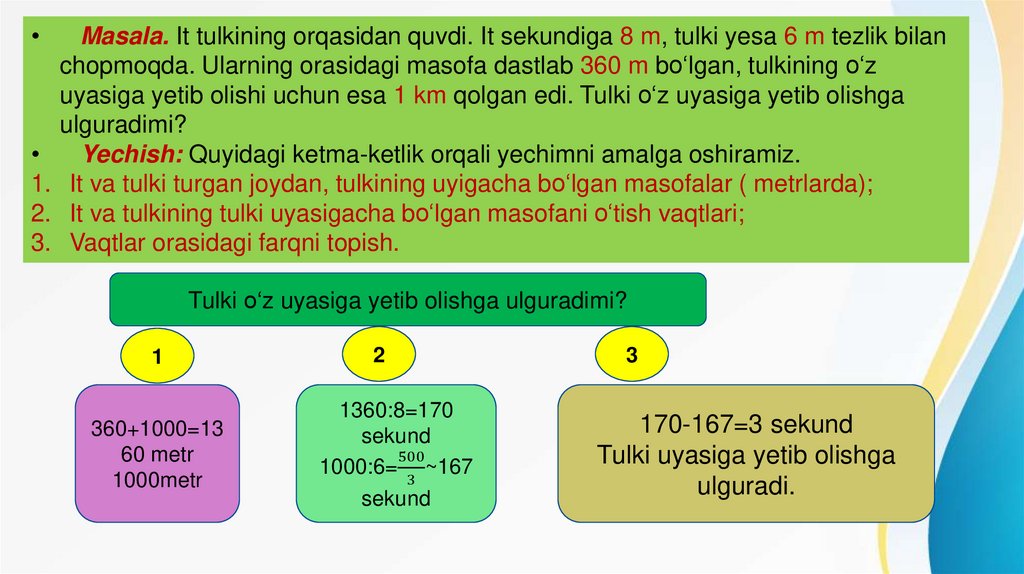
Masala. It tulkining orqasidan quvdi. It sekundiga 8 m, tulki yesa 6 m tezlik bilan
chopmoqda. Ularning orasidagi masofa dastlab 360 m bо‘lgan, tulkining о‘z
uyasiga yetib olishi uchun esa 1 km qolgan edi. Tulki о‘z uyasiga yetib olishga
ulguradimi?
Yechish: Quyidagi ketma-ketlik orqali yechimni amalga oshiramiz.
1. It va tulki turgan joydan, tulkining uyigacha bо‘lgan masofalar ( metrlarda);
2. It va tulkining tulki uyasigacha bо‘lgan masofani о‘tish vaqtlari;
3. Vaqtlar orasidagi farqni topish.
Tulki о‘z uyasiga yetib olishga ulguradimi?
1
360+1000=13
60 metr
1000metr
2
1360:8=170
sekund
500
1000:6= ~167
3
sekund
3
170-167=3 sekund
Tulki uyasiga yetib olishga
ulguradi.

29.

Xulosa va takliflar
Shunday qilib masalalarni arifmetik usulda yechish jarayonida о‘quvchilar yangi matematik
bilimlarini egallaydilar, amaliy faoliyatga tayyorlana boradilar. Bunda о‘quvchining matnli masala va
uning tuzilishi haqida chuqur tasavvurga ega bо‘lishi, masalalarni turli usullar bilan yecha olishi
muhimdir. Shu jihatdan matnli masalani quyidagicha ifodalash mumkin. Matnli masala biror
vaziyatning tabiiy tildagi ifodasi bо‘lib, unda bu vaziyatning biror qismiga miqdoriy tavsif berish,
qismlari orasidagi bog‘lanishlar, munosabatlar bor-yо‘qligini, va uning turini aniqlash talab etiladi.
Dunyodagi rivojlangan mamlakatlar o’z oldiga nafaqat mahsulot ishlab chiqarishni ko’paytirish va
ularni bozorga olib chiqishni, balki chuqur bilim va ilmiy yutuqlarga asoslangan innovatsion
iqtisodiyotga o’tish vazifasini qo’ygan. Ta’lim tizimini isloh qilish va unga hamohang dastur hamda
darsliklarni yaratish mamlakatimizda mustaqillikning dastlabki kunlaridanoq zaruriy ehtiyojga aylandi.
Ayni shu maqsadda darslik vazifasini, uning g‘oyaviy yo‘nalishini mustaqillik ehtiyoji nuqtai nazaridan
qayta tahlil etilib, bir qator tavsiya maqomiga ega bo‘lgan qo‘llanmalar yaratildikim, ular uzluksiz
ta’lim tizimidan darsliklarning dunyoga kelishida dasturulamal bo‘lib xizmat qildi. Lekin zamon shiddat
bilan rivojlanib bormoqda. Davlatimiz rahbari o’zlari bunga naqadar jon kuydirib aytgan fikrlari bunga
yaqqol misol bo’la oladi. Hozirgi paytda dunyo miqyosida raqobat qanday keskin tus olib borayotganini
hammamiz ko’rib turibmiz. Bu shiddatli raqobatga faqat zamonaviy ilm-fan, yuqori texnologiyalar va
innovatsiya yutuqlarini keng joriy etish orqali munosib javob bera olamiz.

30.

FOYDALANILGAN ADABIYOTLAR:
1. QOSIMOVA, M. (2020). TAQQOSLASHGA DOIR TOPSHIRIQLAR USTIDA ISHLASH
TEXNOLOGIYASI: TAQQOSLASHGA DOIR TOPSHIRIQLAR USTIDA ISHLASH
TEXNOLOGIYASI.
2. Qosimov, F. M., & Qosimova, M. M. (2022). MATEMATIKADAN IJODIY O ‘QUV
TOPSHIRIQLARINING METODIK XUSUSIYATLARI.
3. BOSHQARUV VA ETIKA QOIDALARI ONLAYN ILMIY JURNALI ,2(2), 206-211.
4. Muhammedovich, Q. F., & Muhammedovna, Q. M. (2022). BOSHLANG’ICH SINFDA O’RTA
ARIFMETIK SONNI TOPISHGA DOIR MASALALAR YECHISHGA O’RGATISH
METODIKASI.
5. S.A.Ahmedov,S.Ahmedova “O’rta Osiyoda arifmetika taraqqiyoti va uning o’qitish tarixi“
Toshkent, 1991y.35-36-bet.
6. Quzmanova G.B (2021) Umumiy о‘rta ta’lim maktablarida matnli masalalarni ta’limiy. 11541159.
7. Musurmonova M. “Boshlang’ich sinf o’quvchilarida matematikadan masalalar yechish
ko’nikmasini shakllantirishning metodik imkoniyatlari”. 2181 – 7138,№6 2021 jild
8. Musurmonova M.” Boshlang’ich sinf o’quvchilariga uzunlik va yuza o’lchov birliklarini o’rgatish
usullari”

31.

E’tiboringiz
uchun
rahmat