Непрерывная случайная величина

1. Непрерывная случайная величина.

2.

Случайной называется величина,
которая в результате опыта может
принять то или иное возможное
значение, неизвестное заранее, но
обязательно одно.

3.

Непрерывной случайной величиной (НСВ)
называют такую случайную величину, которая
может принять любое значение из некоторого
конечного или бесконечного интервала.

4. Аналитический способ задания закона распределения

Дифференциальной функцией распределения
или плотностью распределения вероятностей
называется первая производная интегральной
функции распределения.

5. Свойства дифференциальной функции распределения

1.
Для любых х дифференциальная функция распределения
неотрицательна, т.е.
2.
Для дифференциальной функции распределения имеет место
равенство
3.
Для дифференциальной функции распределения имеет место
равенство
4.
Для интегральной и дифференциальной функций
распределения имеет место равенство

6.

Числовые характеристики
случайной величины
Математическим
ожиданием непрерывной
случайной величины, возможные значения
которой принадлежат отрезку [a, b], называется
определенный интеграл
Если возможные значения случайной величины
распределены по всей оси Ох, то

7.

2. Дисперсия НСВ

8. Пример

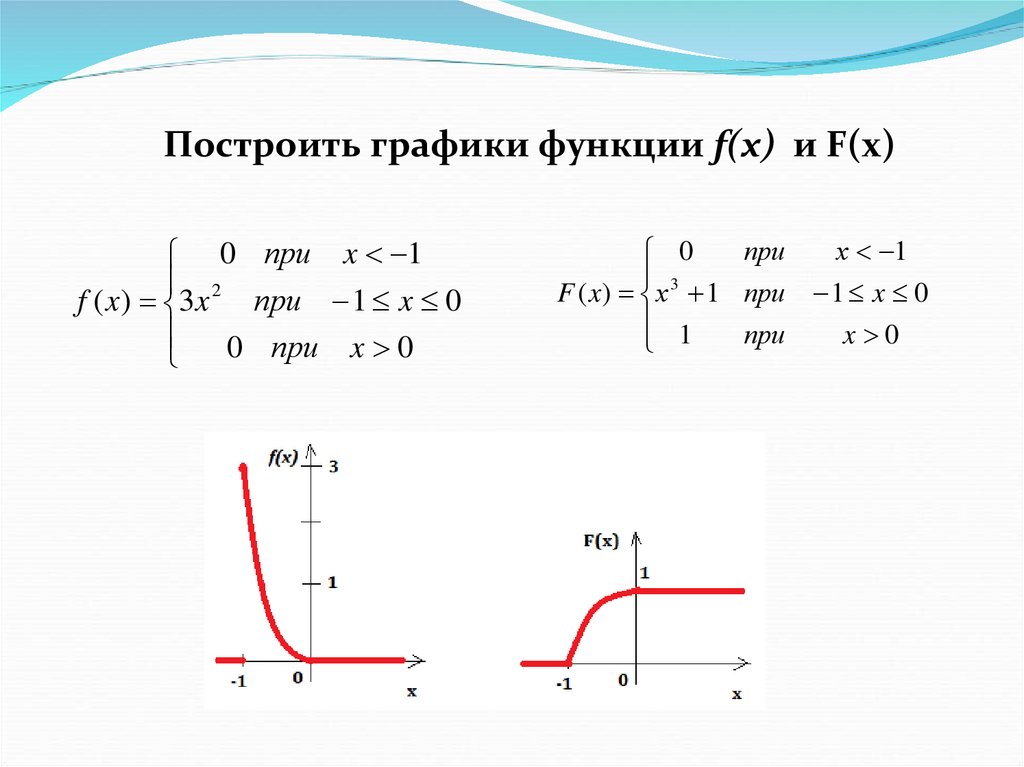
Случайная величина задана дифференциальной
функцией распределения
0 при x 1
f ( x) 3x 2 при 1 x 0
0 при x 0
1. Найти интегральную функцию распределения и
построить графики функции f(x) и F(x)
2. Найти математическое ожидание и дисперсию
этой случайной величины.

9. Решение

Найти интегральную функцию распределения.
Воспользуемся формулой
x
если
х 1
F ( x) 0dt 0
1
х
3t 3 x
3
3
3
если 1 х 0 F ( x) 0dt 3t dt 0
1 x ( 1) x 1
3
1
2
1
если
0
x
3t 3 0
3
3
х 0 F ( x) 0dt 3t dt 0dt 0
0
0
(
1
)
1
1
3
1
0
2
Таким образом,
при
х 1
0
F ( x) х 3 1 при 1 x 0
1
при
x 0

10.

Построить графики функции f(x) и F(x)
0 при x 1
f ( x) 3x 2 при 1 x 0
0 при x 0
при
х 1
0
F ( x) х 3 1 при 1 x 0
1
при
x 0

11.

Найти математическое ожидание этой
случайной величины.
Воспользуемся формулой
1
0
0
4
3
x
3
0
MX хf ( x)dx x 0dx x 3x 2 dx x 0dx 3x 3 dx
1
4
4
1
0
1

12.

Найти дисперсию этой случайной величины.
Воспользуемся формулой
3
3
9
DX ( x ) 2 3 x 2 dx x 4 x 3 x 2 dx
4
2
16
1
1
0
0
x 5 3x 4 3x 3 0
( 1) 5 3( 1) 4 3( 1) 3 3
1 0 3
3
0.0375
8
16
8
16 80
5
5