Лекция 4. Раздел 4. Элементы линейной алгебры и аналитической геометрии. §1. Матрицы. Операции над ними

1. Раздел 4. Элементы линейной алгебры и аналитической геометрии

Лекция 4
Раздел 4. Элементы линейной алгебры и
аналитической геометрии
§1. Матрицы. Операции над ними

2.

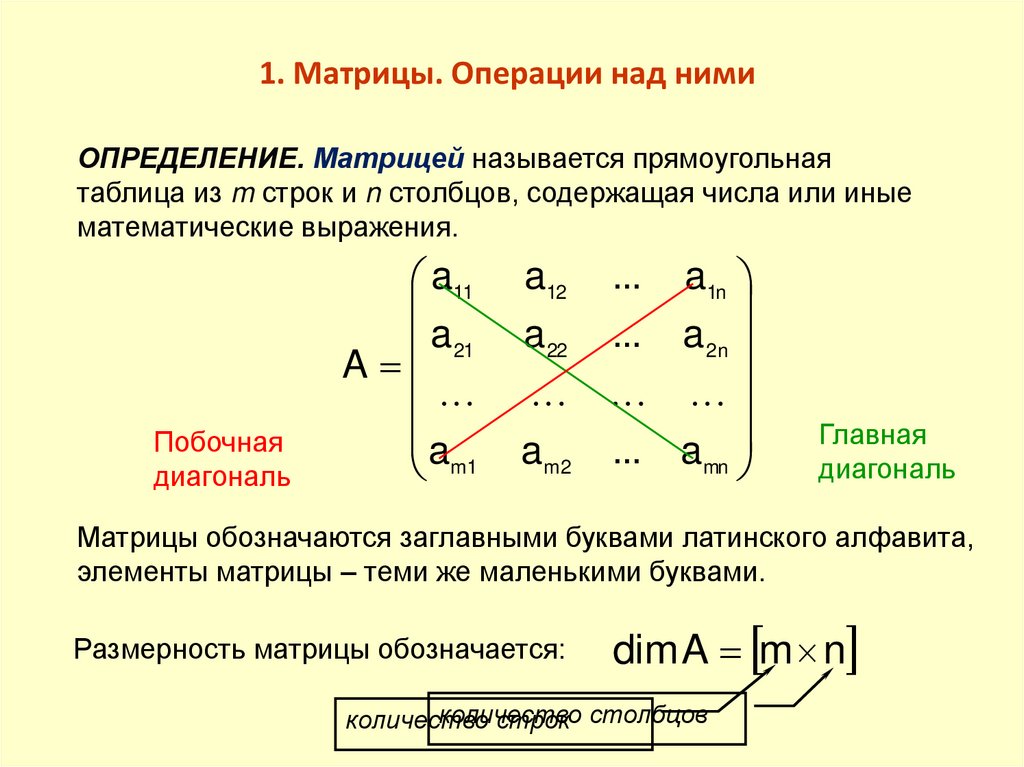
1. Матрицы. Операции над ними
ОПРЕДЕЛЕНИЕ. Матрицей называется прямоугольная
таблица из m строк и n столбцов, содержащая числа или иные
математические выражения.
Побочная
диагональ
a11
a 21
A
a
m1
a12 ... a1n
a 22 ... a 2n
am 2 ... amn
Главная
диагональ
Матрицы обозначаются заглавными буквами латинского алфавита,
элементы матрицы – теми же маленькими буквами.
Размерность матрицы обозначается:
dim A m n
количество
количество
строк столбцов

3. Виды матриц

1) Если m n , то матрица называется прямоугольной.
2) Если m n , то матрица называется квадратной (n - ного
порядка).
3) Матрица, состоящая из одной строки называется векторстрока:
a a
11
12
a13 ... a1n
Матрица , состоящая из одного столбца
называется вектор-столбец:
a11
a 21
...
a
m1

4.

4) Квадратная матрица называется единичной, если ее
элементы, расположенные на главной диагонали, равны
единице, остальные – нулю (обозначается буквой Е):
1 0 0
E 0 1 0
0 0 1
5) Если все элементы квадратной матрицы равны нулю, то
она называется нулевой матрицей и обозначается
символом 0:
0 0 0
O 0 0 0
0 0 0

5.

6) Квадратная матрица называется диагональной, если
элементы, стоящие вне главной диагонали равны нулю
2 0 0
A 0 3 0
0 0 1
7) Квадратная матрица называется треугольной, если
элементы, стоящие ниже (выше) главной диагонали равны
нулю:
4
0 0
2 5
2
B 0 3 7 C 9 3 0
0 0
2 5 1
1

6. Действия над матрицами

Сравнение матриц
Матрицы равны, если они имеют одинаковую размерность и их
соответствующие элементы равны.
A B
dim A dimB;
aij bij
Сложение (вычитание) матриц
Сумма и разность матриц существуют только для матриц
одинакового размера, при этом соответствующие элементы
матриц складываются или вычитаются.
C A B
dim A dimB dim C
c ij aij bij

7. Действия над матрицами

Транспонирование матрицы
Операция получения из данной матрицы транспонированной
заменой каждой строки столбцом с тем же номером
1 3 2
A
0 1 4
1 0
T
A 3 1
2 4

8.

Умножение матрицы на число
При умножении матрицы A на число k получается матрица того же
размера, при этом каждый элемент матрицы A умножается на k.
B k A
dim A dim B; bi j ai j k
Найти значение выражения:
1 3 2
A
0 1 4
C A 5 B
2 4 1
B
5 0 2
10 20 5
5 B
0 10
25
11 17 7
C A 5 B
25 1 14
Решение:

9.

Умножение матриц
Произведение матриц A * B определено только тогда, когда
число столбцов матрицы А равно числу строк матрицы В, в
противном случае произведение не существует.
dim A m n
dim B n k
C A B существует
dimC m k
Произведением матрицы A размера [m n] с элементами ai j
на матрицу B размера [n k ] с элементами bj p называется
матрица C размера [m k ] с элементами:
n
cip aij b jp
j 1

10.

1 0 2
A
3 1 4
0 5 1
B 2 1 1
3 2 0
0 5 1
B 2 1 1
3 2 0
1 0 2
A
3 1 4
6 9 1
14 24 4
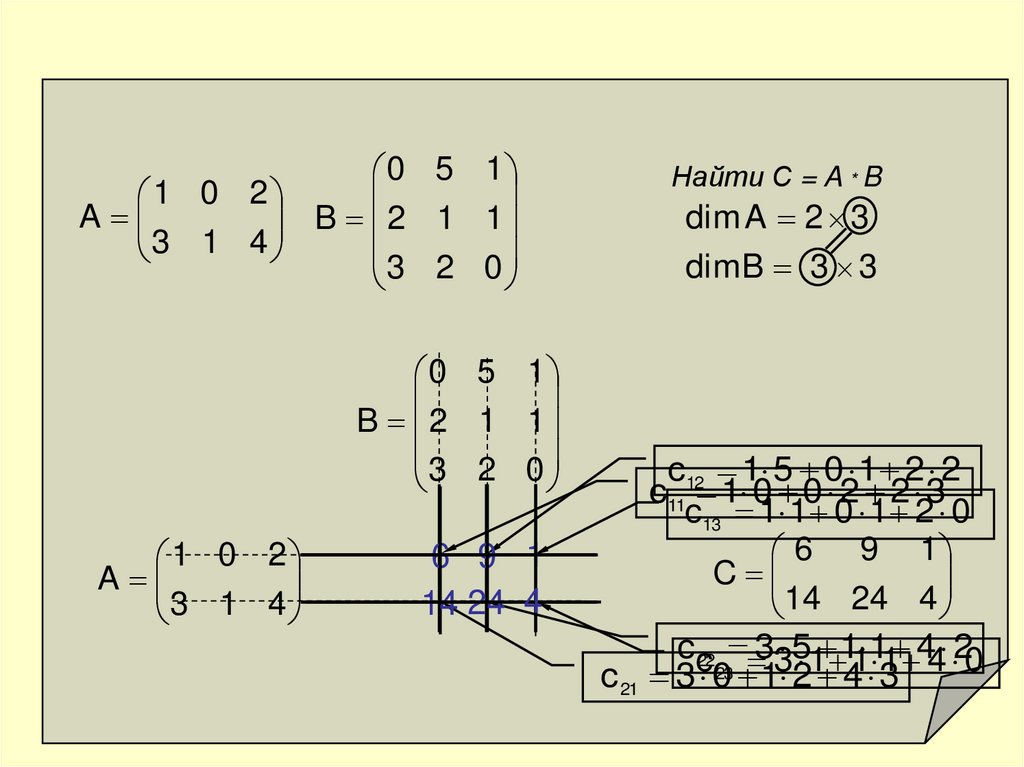
Найти С = A * B
dim A 2 3
dim B 3 3
c12 1 5 0 1 2 2
c11 1 0 0 2 2 3
c13 1 1 0 1 2 0
6 9 1
C
14 24 4
cc22 33 5 1 11 1
44 20
1
c 21 3 023 1 2 4 3

11.

Свойства операций :
1) A B B A
A B C A B C
3) A O O A A
2)
4) A BC AB C
5)
6)
AB A B
A B C AC BC
7) В общем случае для произведения матриц не действует
переместительный закон: A B B A
В случае, когда АВ = ВА, матрицы А и В называются
(перестановочными) коммутативными.
8)
EA AE A