Похожие презентации:
§ 4. Формула интегрирования по частям
1.
§ 4. Формула интегрирования по частямЕсли u x и v x – дифференцируемые функции, то справедлива
формула интегрирования по частям:
udv uv vdu .
Эту формулу используют, когда вычисление интеграла vdu проще, чем
вычисление интеграла
udv . За функцию u удобно принимать
множитель, который упрощается при дифференцировании. Например,
если под знаком интеграла стоит произведение многочлена на
тригонометрическую или показательную функцию, то за функцию u
следует принять многочлен, а оставшееся выражение принять за dv.
В некоторых случаях формула интегрирования по частям может
применяться неоднократно.
Пример. Вычислить x cos xdx .
Положим u x , dv cos xdx du dx ,
x cos xdx x sin x sin xdx x sin x cos x C .
v cos xdx sin x
2.
Еслиподынтегральная
функция содержит сомножителем
логарифмические или обратные тригонометрические функции, то их
следует принимать за функцию u, так как в результате
дифференцирования эти функции упрощаются.
Пример. Вычислить ln xdx .
Положим
u ln x ,
dv dx .
Имеем
du
dx
,
x
v dx x .
dx
Следовательно ln xdx x ln x x x ln x x C .
x
Иногда после двукратного применения формулы интегрирования по
частям приходим в правой части к выражению, содержащему исходный
интеграл. Другими словами, получаем уравнение с искомым интегралом
в качестве неизвестного.
3.
§ 5. Интегрирование простейших рациональных дробейЦелой рациональной функцией аргумента x называют функцию вида
Pn x a0 x n a1 x n 1 ... an 1 x an ,
где n – натуральное число, называемое степенью многочлена, ai
i 0,1,...,n – постоянные коэффициенты.
Дробной рациональной функцией (рациональной дробью) называют
функцию вида
Pm x
,
f x
Qn x
где Pm x – многочлен степени m, Qn x – многочлен степени n.
Рациональную дробь называют правильной, если m n , и
неправильной, если m n .
3x 2 1
Пример. Функция
– правильная рациональная дробь,
3
5x 1
3x 2 1
4 x
функция
– неправильная рациональная дробь, функция
–
2
2
4x 1
2x 1
нерациональная функция.
4.
P xделением
Q x
числителя на знаменатель можно представить в виде суммы многочлена
R x
. Другими словами, можно
L x и правильной рациональной дроби
Q x
написать
P x
R x
.
L x
Q x
Q x
Пример. Представить неправильную рациональную
дробь
P x x 3 4 x 7
в виде суммы многочлена L x и правильной
Q x
x 1
R x
рациональной дроби
.
Q x
Разделив
числитель
дроби
на
знаменатель,
получим
P x x 3 4 x 4 x 3 x 2 x 2 x 3x 3 4
4
2
x x 3
, где
Q x
x 1
x 1
x 1
Всякую неправильную рациональную дробь вида
L x x 2 x 3 – частное, R x 1 – остаток.
5.
Простейшими рациональными дробями 1, 2, 3 и 4 типов называютправильные рациональные дроби вида
A
1)
;
x a
A
2)
; n – натуральное число,
n
x a
p2
Mx N
q 0;
3) 2
,
x px q 4
Mx N
p2
q 0.
4)
, n – натуральное число, n 2 ,
n
2
4
x px q
В этих выражениях A, a, M, N, p, q – действительные числа.
Найдем интегралы от простейших рациональных дробей.
6.
Ad x a
dx A
A ln x a C .
x a
x a
n 1
A
x a
n
dx A x a d x a A
C.
2)
n
n 1
x a
Mx N
p
dx . Сделаем подстановку x z .
3) 2
2
x px q
1)
Имеем
p2
p
a 2 . Тогда получим
x z , dx dz . Обозначим q
2
4
p
M z N
Mx N
Mx N
2
dx
dx
dz
x 2 px q p 2
2
2
2
z a
p
x q
2
4
zdz
Mp
dz
M 2
N
2
2
2
2 z a
z a
7.
MMp 1
z
ln z 2 a 2 N
arctg
C
2
2 a
a
Mp
p
N
x
M
2 arctg
2 C.
ln x 2 px q
2
p2
p2
q
q
4
4
p
Mx N
.
Сделаем
подстановку
dx
x
z . Имеем
x 2 px q n
2
4)
p2
p
a 2 . Тогда получим
x z , dx dz . Обозначим q
4
2
Mx N
zdz
Mp
dz
x 2 px q n dx M z 2 a 2 n N 2 z 2 a 2 n .
zdz
Вычислим интеграл
. Имеем
2
2 n
z a
zdz
1 d z2 a2
1
z 2 a 2 n 2 z 2 a 2 n 2 1 n z 2 a 2 n 1 C .
8.
Вычислим интегралdz
z a
2 n
2
, обозначив его через I n . Имеем
1 z 2 a2 z 2
In
2
dz
n
2
2 n
2
2
a
z a
z a
dz
2
1
1
dz
z2
z
2
dz 2 I n 1
dz ,
n
1
n
n
a
a z 2 a 2
z2 a2
z2 a2
где обозначено I n 1
dz
z a
2 n 1
2
. Применим к интегралу
z2
z a
2
метод интегрирования по частям. Для этого положим u z . Тогда
zdz
получим du dz , dv
,
2
2 n
z a
zdz
1 d z2 a2
1
.
v
n
n
n
1
2 z 2 a2
z2 a2
2 1 n z 2 a 2
2 n
dz
9.
Следовательноz2
z 2 a 2
dz
n
z
2 1 n z 2 a 2
z
n 1
1
dz
n 1
2
2
2 1 n z a
1
I n 1 .
2
2 n 1
2 1 n
2 1 n z a
Тогда получим
1 2n 3
z
.
In 2
I n 1
n
1
a 2n 2
2 1 n z 2 a 2
Таким образом, степень n знаменателя дроби понизилась на единицу.
В общем случае, чтобы проинтегрировать правильную
P x
рациональную дробь m , m n , ее следует предварительно разложить
Qn x
в сумму простейших дробей. Неизвестные коэффициенты в числителях
дробей находят методом неизвестных коэффициентов.
10.
x2 1Пример. Найти 3
dx .
2
x 2x x
x2 1
x2 1
A
B
C
Имеем 3
2
2
2
x x 1 x 1
x 2 x x x x 1
A x 1 Bx x 1 Cx
2
x x 1
2
x 2 A B x 2 A B C A
x x 1
2
x 2 A B x 2 A B C A
.
x x 1
Чтобы это соотношение выполнялось при любом x, необходимо
A B 1, 2 A B C 0, A 1.
положить
Отсюда
получим
A 1, B 0, C 2 . Следовательно
2
x2 1
1
2
2
x 3 2 x 2 x dx x dx x 1 2 dx ln x x 1 C





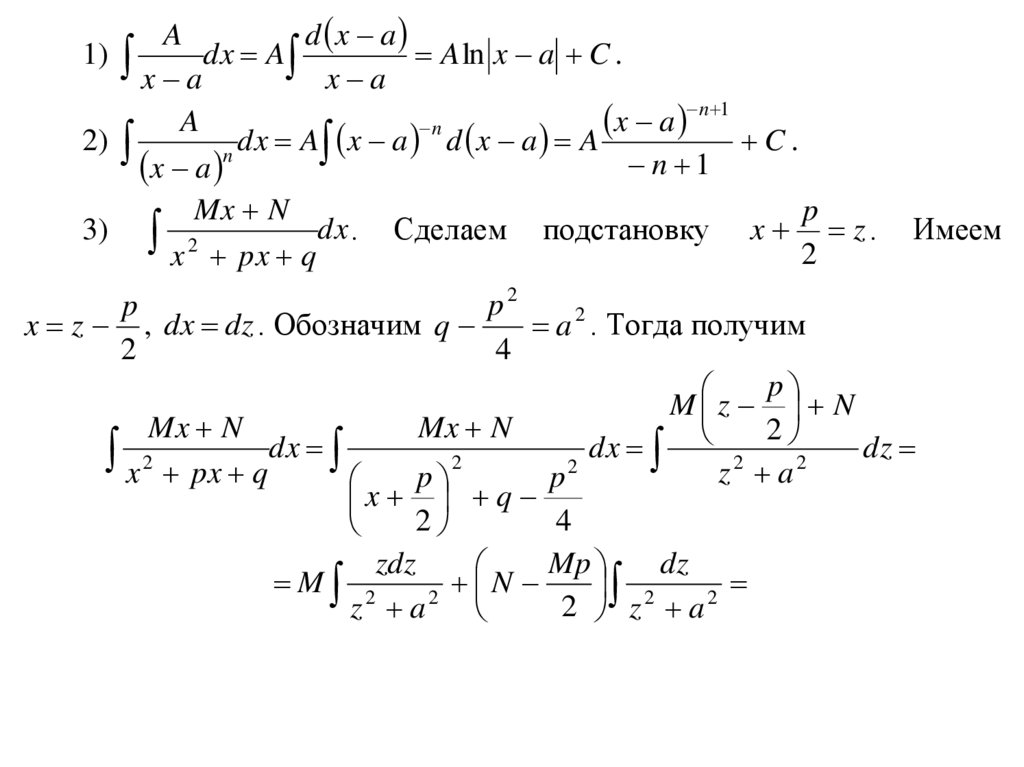




 Математика
Математика








