ЛЕКЦИЯ 6 - Позиционные задачи (1)

1.

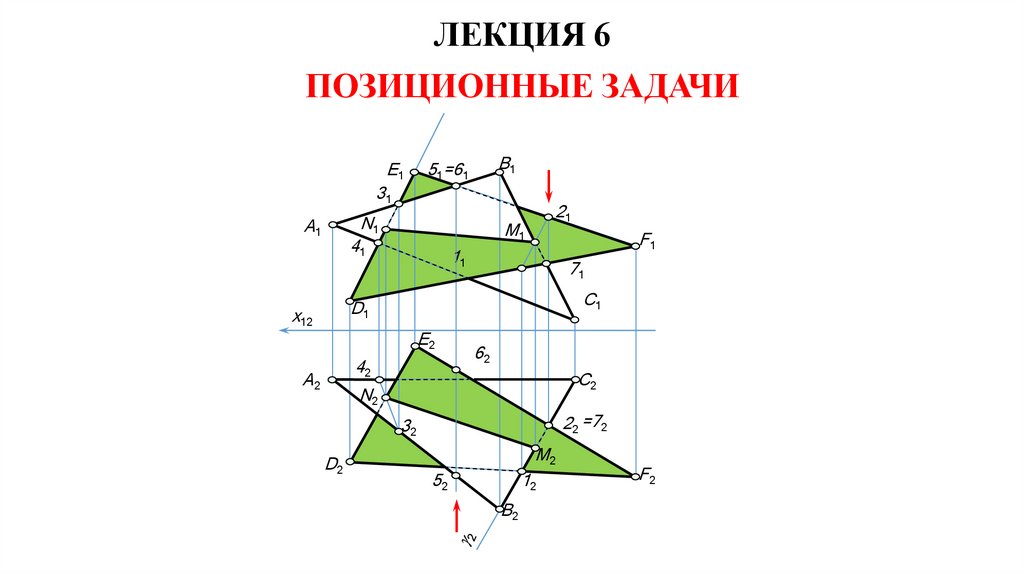
ЛЕКЦИЯ 6
ПОЗИЦИОННЫЕ ЗАДАЧИ
E1
B1
51=61
31
N1
A1
21
M1
41
F1
11
71
C1
D1
x12
E2
42
A2
62
C2
N2
22 =72
32
D2
M2
52
12
B2
F2

2.

Основные позиционные задачи
Сениор-лектор Жаркимбаева Гульнара Бахитовна

3.

Основные позиционные задачи
Задачи, в которых определяется взаимное расположение
точек, прямых и плоскостей, называются позиционными.
Всего определяют шесть позиционных задач:
1. Взаимное расположение точек;
2. Взаимное расположение точек и прямой;
3. Взаимное расположение двух прямых;
4. Взаимное расположение точек и плоскости;
5. Взаимное расположение прямой и плоскости;
6. Взаимное расположение плоскостей.

4.

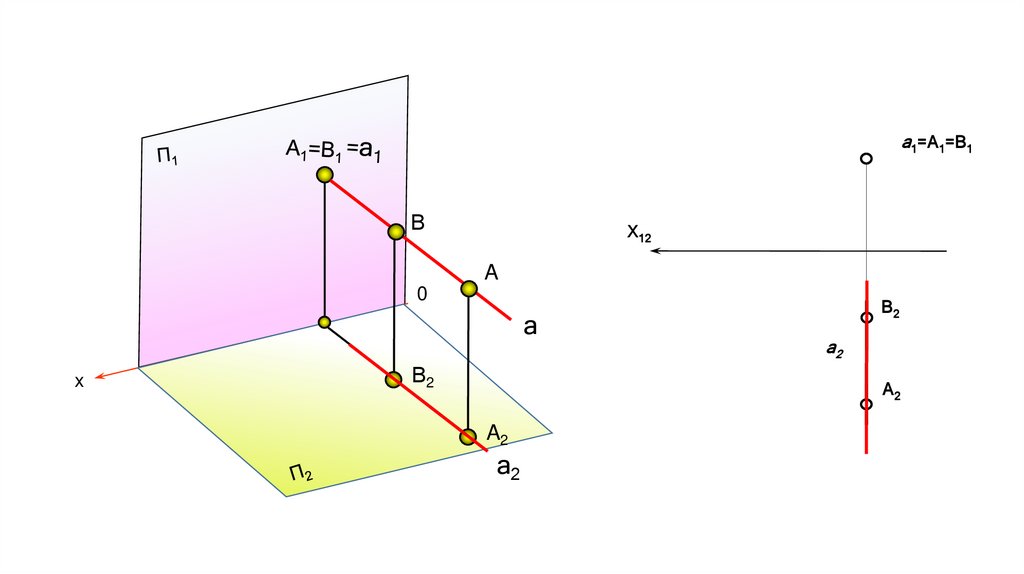
1. Взаимное расположение точек.
а1=А1=В1
D1
b1
X12
X12
С1
В2
а2
b 2= С 2= D 2
A2
а) фронтально конкурирующие точки А и В
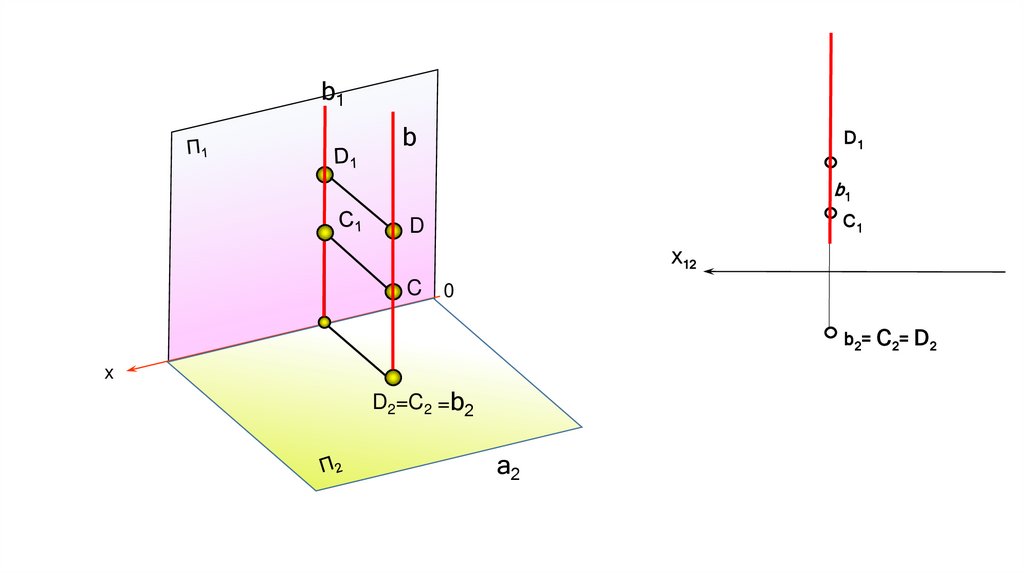
б) горизонтально конкурирующие точки C и D
В начертательной геометрии интерес представляют точки, расположенные на проецирующих прямых, так называемые конкурирующие
точки.
На рисунке а) показаны фронтально конкурирующие точки А и В; фронтальные проекции точек совпадают, прямая а является
фронтально проецирующей (фронтальная проекция прямой вырождается в точку).
На рисунке б) показаны горизонтально конкурирующие точки С и D; горизонтальные проекции точек совпадают, прямая b является
горизонтально проецирующей (горизонтальная проекция прямой вырождается в точку).
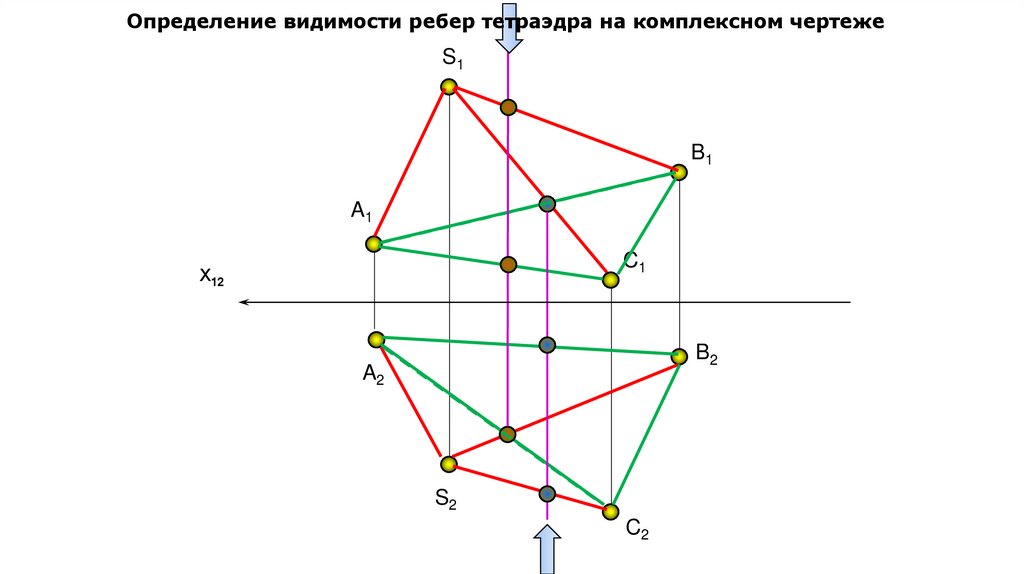
Конкурирующие точки применяют при определении видимости геометрических элементов на эпюре (Способ конкурирующих точек).

5.

а1=А1=В1
В
X12
A
0
а
x
В2
В2
а2
A2
A2
а2

6.

b1
b
D1
b1
С1
D
X12
C 0
b 2= С 2= D 2
x
D2=C2 =b2
а2

7.

Определение видимости ребер тетраэдра на комплексном чертеже
S1
B1
A1
C1
X12
B2
A2
S2
C2

8.

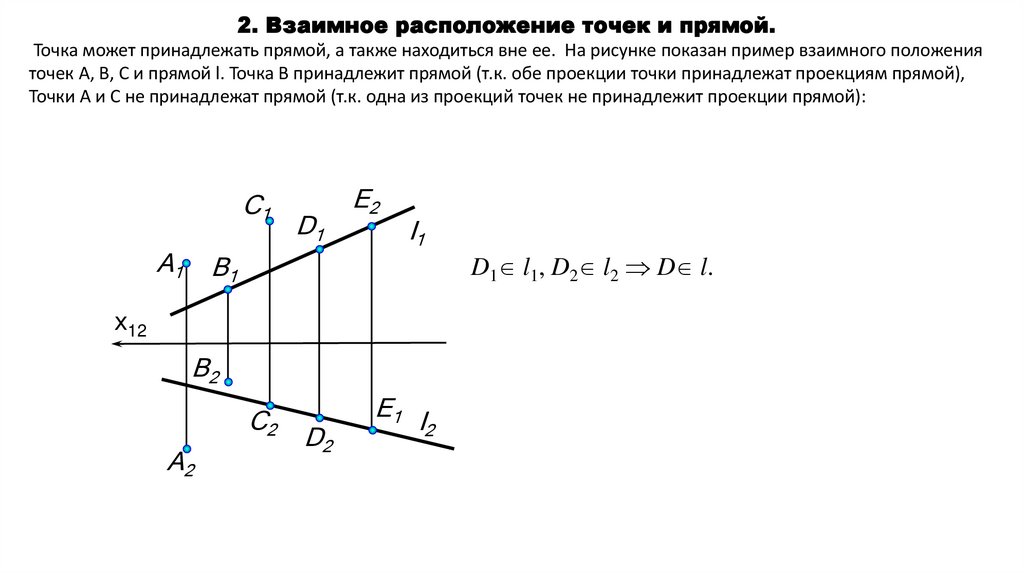
2. Взаимное расположение точек и прямой.
Точка может принадлежать прямой, а также находиться вне ее. На рисунке показан пример взаимного положения
точек А, В, С и прямой l. Точка В принадлежит прямой (т.к. обе проекции точки принадлежат проекциям прямой),
Точки А и С не принадлежат прямой (т.к. одна из проекций точек не принадлежит проекции прямой):
С1
А1
D1
E2
l1
D1 l1, D2 l2 D l.
В1
х12
В2
C2
А2
D2
E1 l
2

9.

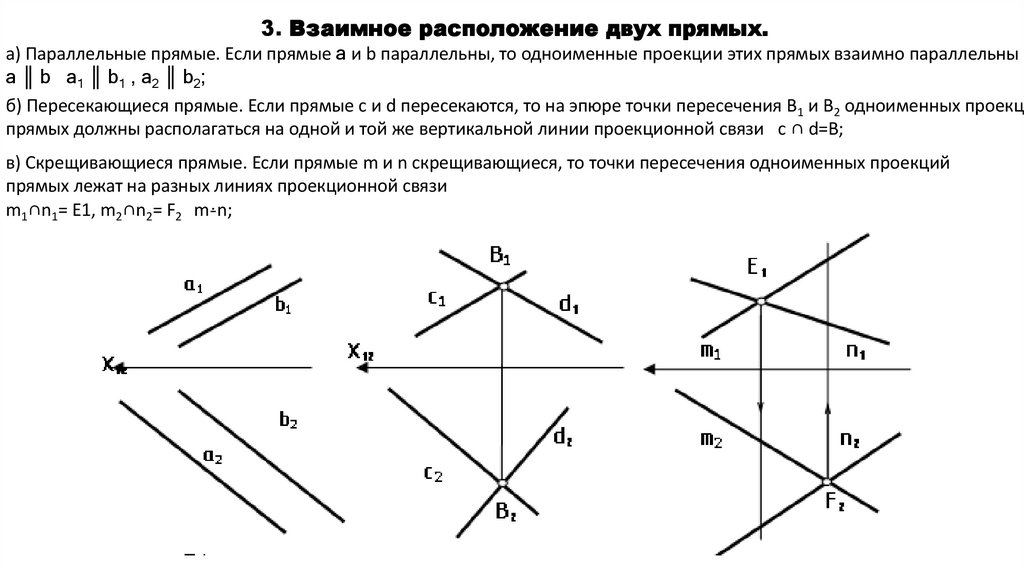
3. Взаимное расположение двух прямых.
а) Параллельные прямые. Если прямые а и b параллельны, то одноименные проекции этих прямых взаимно параллельны
а ║ b а1 ║ b1 , а2 ║ b2;
б) Пересекающиеся прямые. Если прямые c и d пересекаются, то на эпюре точки пересечения B1 и B2 одноименных проекци
прямых должны располагаться на одной и той же вертикальной линии проекционной связи c ∩ d=B;
в) Скрещивающиеся прямые. Если прямые m и n скрещивающиеся, то точки пересечения одноименных проекций
прямых лежат на разных линиях проекционной связи
m1∩n1= E1, m2∩n2= F2 mꜙn;

10.

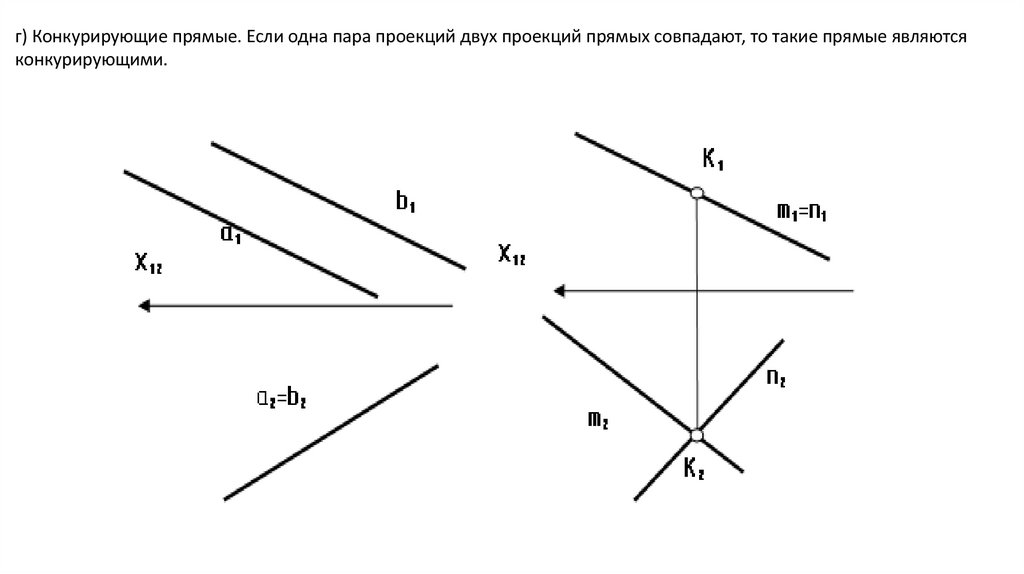
г) Конкурирующие прямые. Если одна пара проекций двух проекций прямых совпадают, то такие прямые являются
конкурирующими.

11.

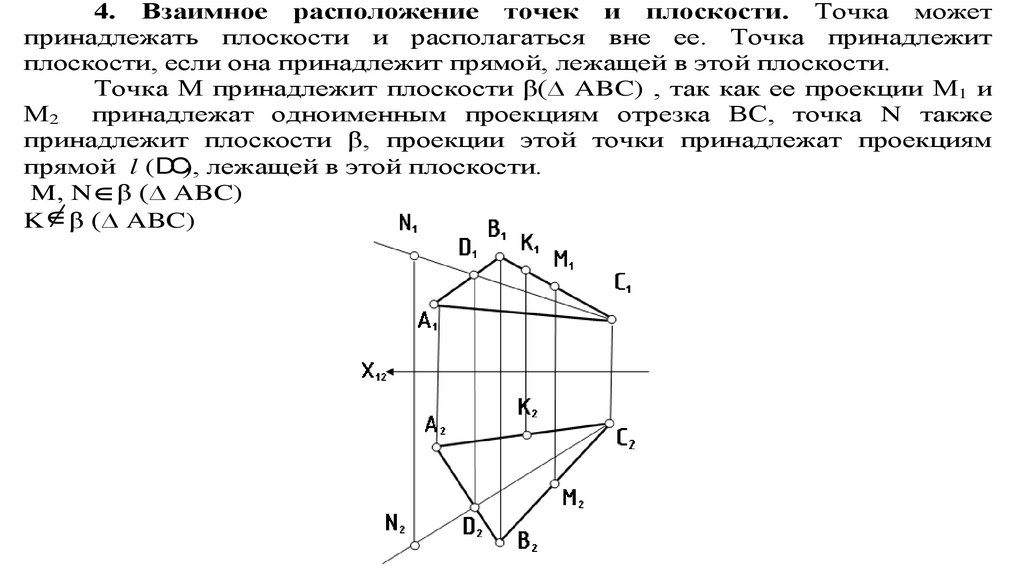
4. Взаимное расположение точек и плоскости. Точка может
принадлежать плоскости и располагаться вне ее. Точка принадлежит
плоскости, если она принадлежит прямой, лежащей в этой плоскости.
Точка М принадлежит плоскости β(∆ ABC) , так как ее проекции М1 и
М2 принадлежат одноименным проекциям отрезка ВС, точка N также
принадлежит плоскости β, проекции этой точки принадлежат проекциям
прямой l (DС), лежащей в этой плоскости.
M, N β (∆ ABC)
K β (∆ ABC)

12.

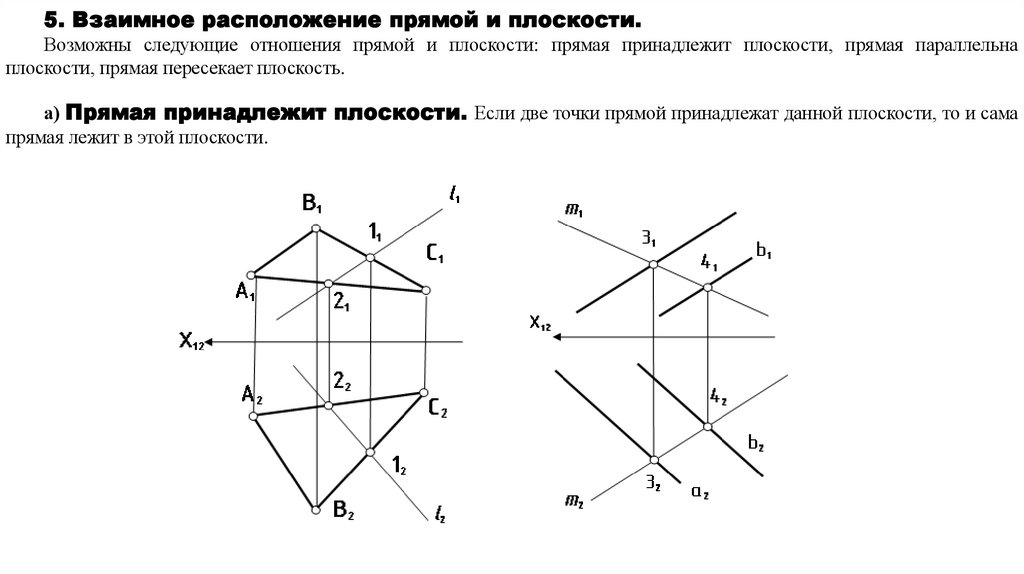
5. Взаимное расположение прямой и плоскости.
Возможны следующие отношения прямой и плоскости: прямая принадлежит плоскости, прямая параллельна
плоскости, прямая пересекает плоскость.
а) Прямая принадлежит плоскости. Если две точки прямой принадлежат данной плоскости, то и сама
прямая лежит в этой плоскости.

13.

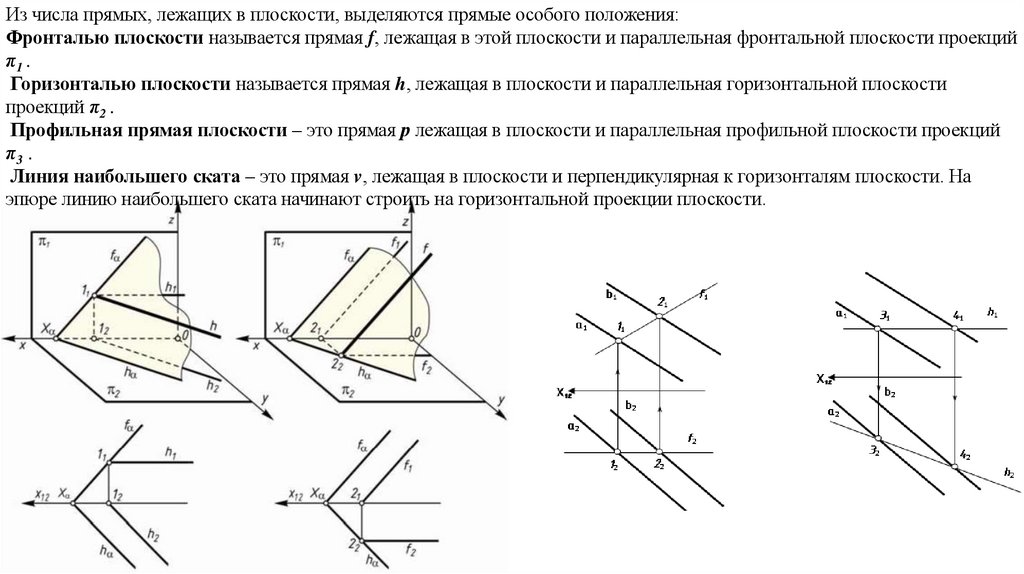
Из числа прямых, лежащих в плоскости, выделяются прямые особого положения:
Фронталью плоскости называется прямая f, лежащая в этой плоскости и параллельная фронтальной плоскости проекций
π1 .
Горизонталью плоскости называется прямая h, лежащая в плоскости и параллельная горизонтальной плоскости
проекций π2 .
Профильная прямая плоскости – это прямая р лежащая в плоскости и параллельная профильной плоскости проекций
π3 .
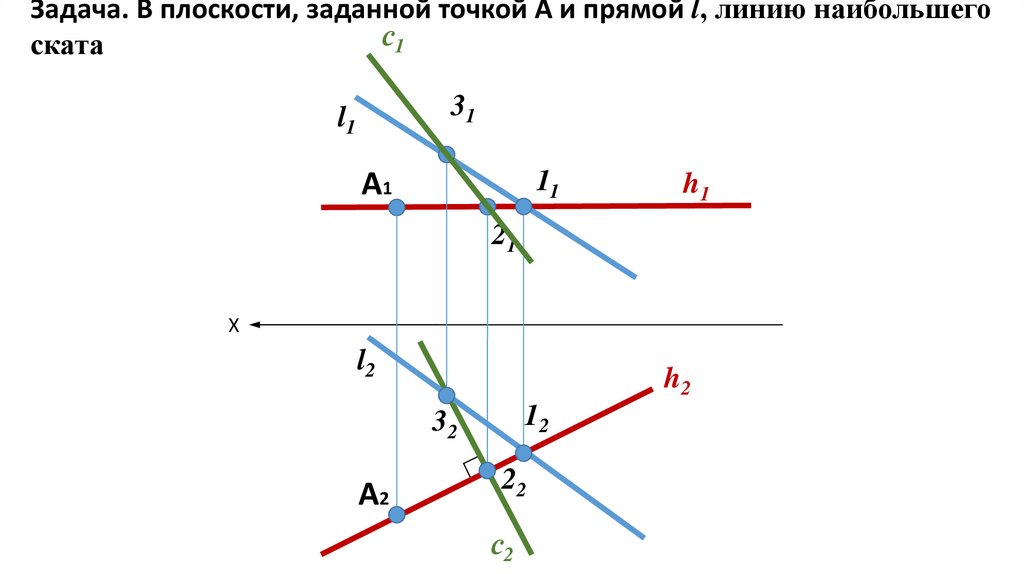
Линия наибольшего ската – это прямая v, лежащая в плоскости и перпендикулярная к горизонталям плоскости. На
эпюре линию наибольшего ската начинают строить на горизонтальной проекции плоскости.

14.

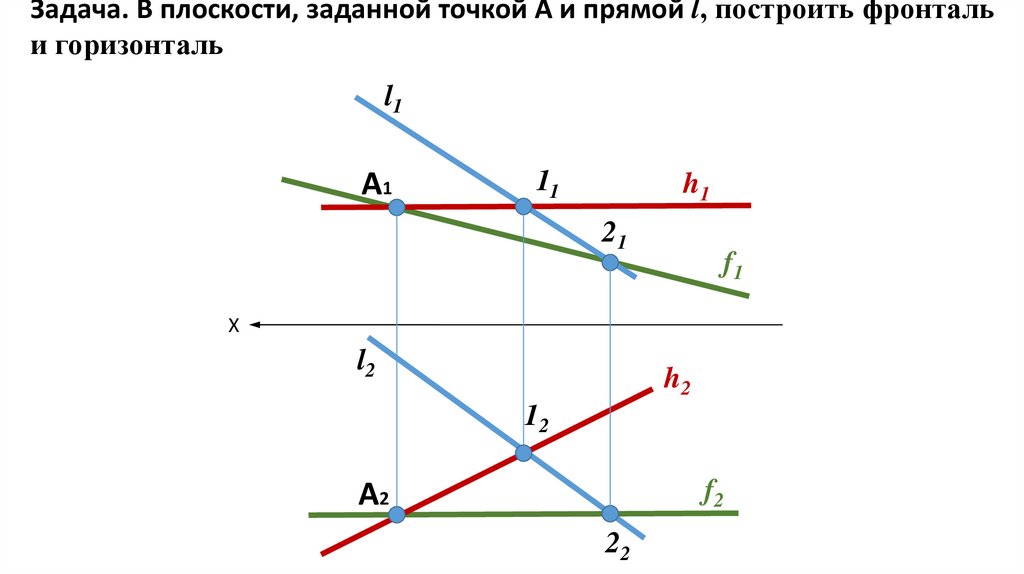
Задача. В плоскости, заданной точкой А и прямой l, построить фронталь
и горизонталь
l1
А1
11
h1
21
f1
Х
l2
h2
12
А2
f2
22

15.

Задача. В плоскости, заданной точкой А и прямой l, линию наибольшего
с1
ската
31
l1
А1
11
h1
21
Х
l2
h2
12
32
А2
22
с2

16.

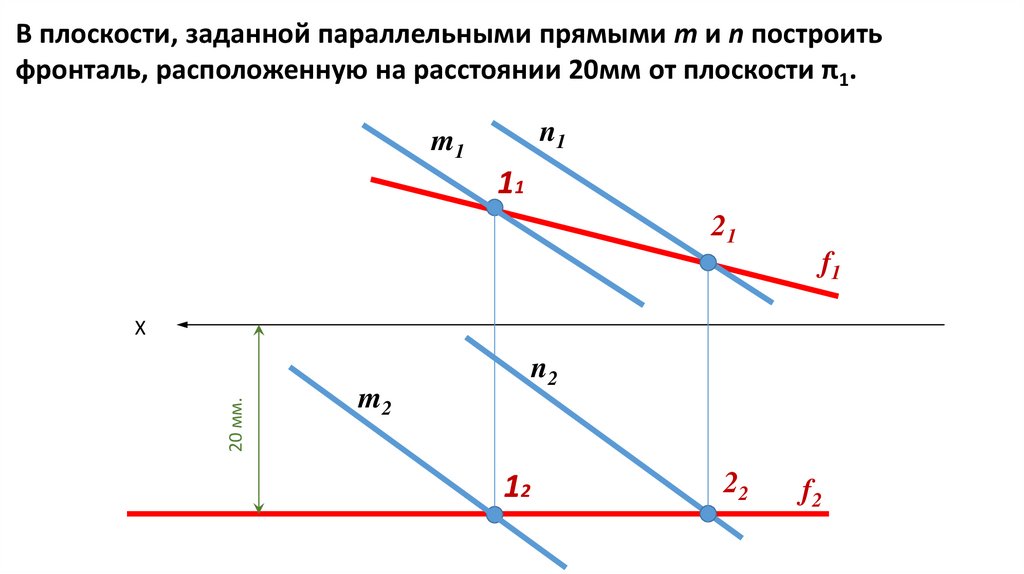
В плоскости, заданной параллельными прямыми m и n построить
фронталь, расположенную на расстоянии 20мм от плоскости π1.
n1
m1
11
21
f1
20 мм.
Х
n2
m2
12
22
f2

17.

.
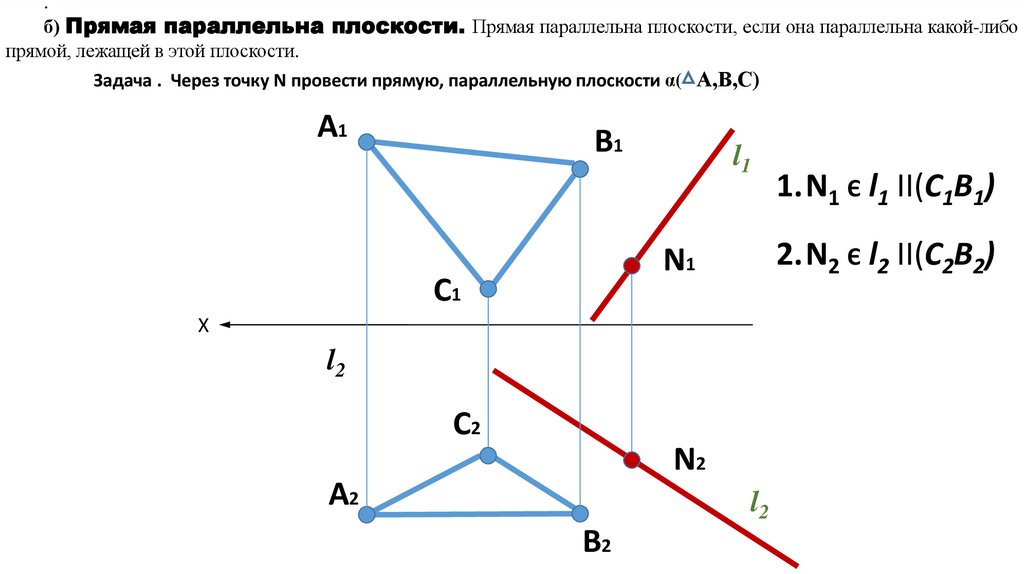
б) Прямая параллельна плоскости. Прямая параллельна плоскости, если она параллельна какой-либо
прямой, лежащей в этой плоскости.
Задача . Через точку N провести прямую, параллельную плоскости α( А,В,С)
А1
B1
l1
2.N2 Є l2 II(C2B2)
N1
C1
Х
l2
C2
N2
А2
l2
B2
1.N1 Є l1 II(C1B1)

18.

.
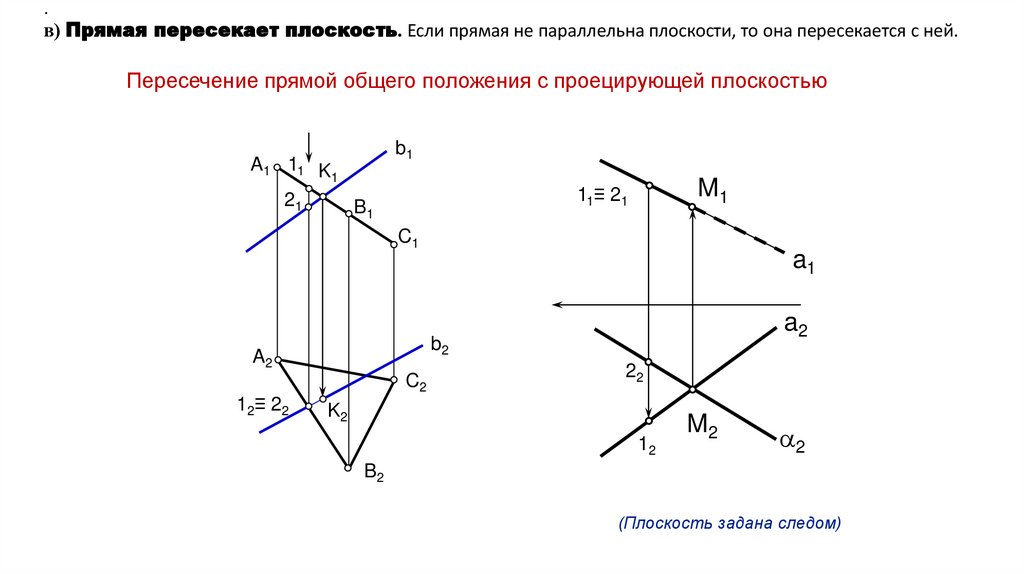
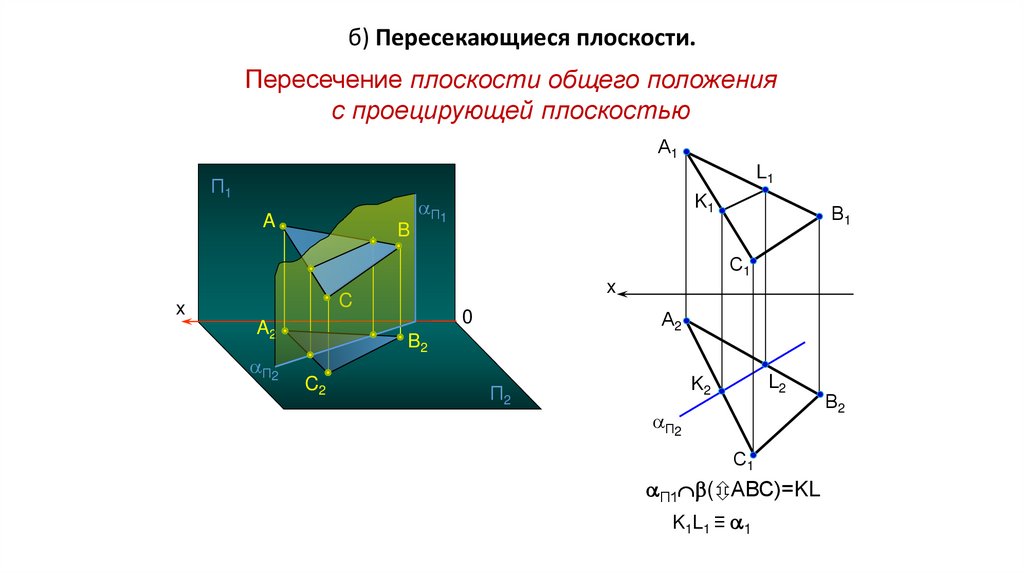
в) Прямая пересекает плоскость. Если прямая не параллельна плоскости, то она пересекается с ней.
Пересечение прямой общего положения с проецирующей плоскостью
A1 11 K
1
21
B1
b1
M1
11≡ 21
C1
a2
b2
A2
12≡ 22
a1
C2
22
K2
12
M2
2
B2
(Плоскость задана следом)

19.

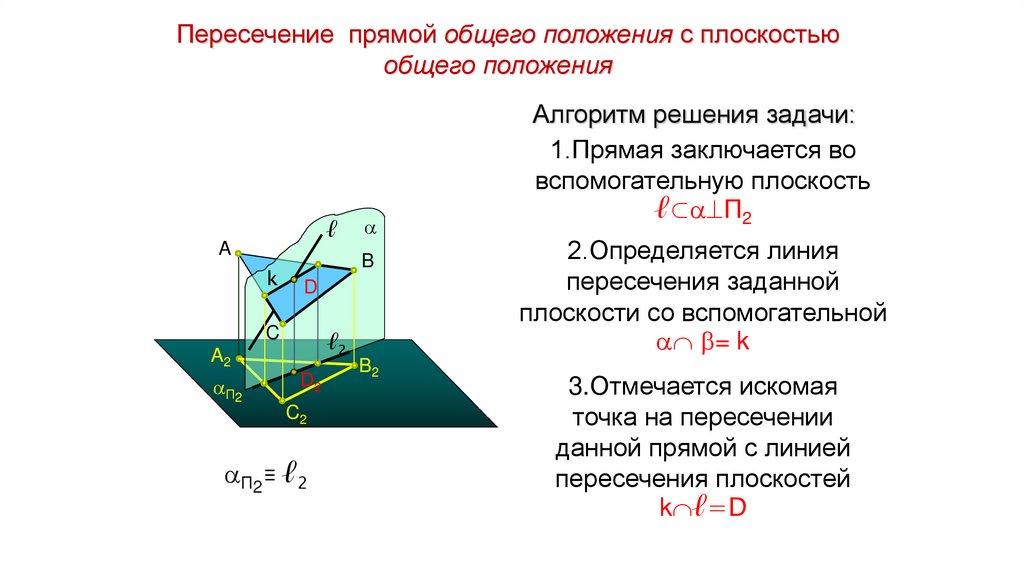
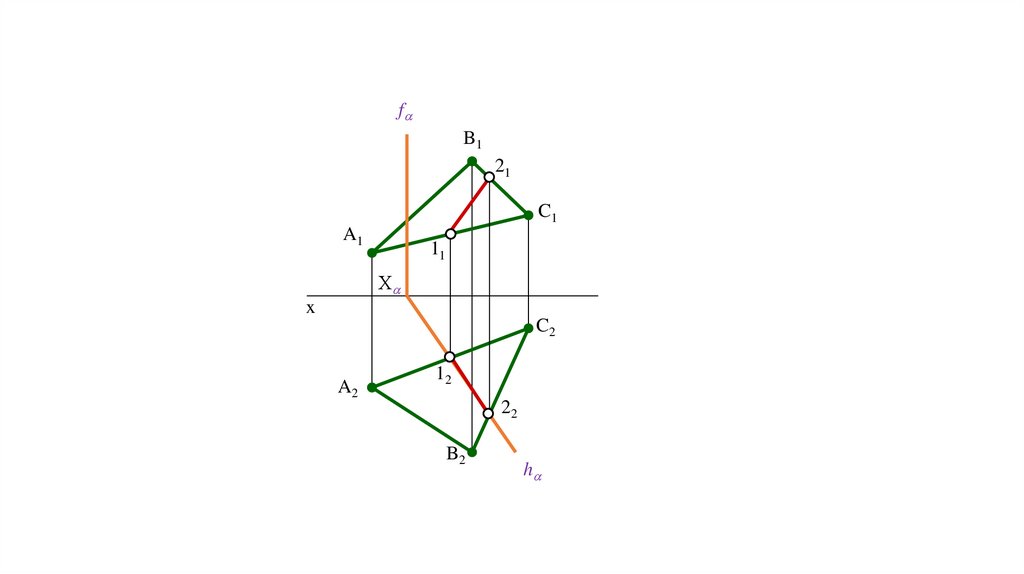
Пересечение прямой общего положения с плоскостью
общего положения
ℓ
A
k
B
D
C
ℓ2
A2
П2
D2
C2
П2 ≡ ℓ2
B2
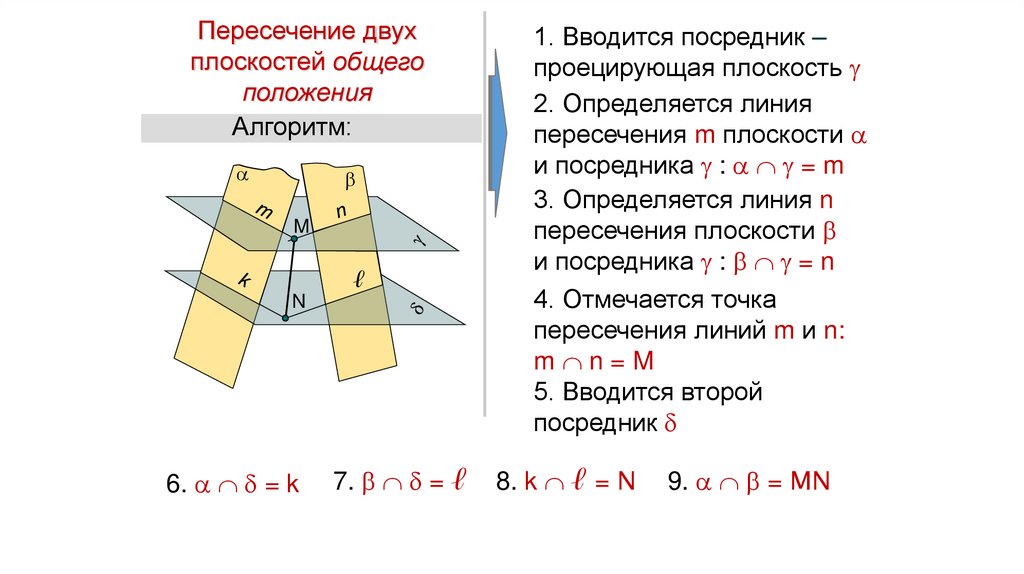
Алгоритм решения задачи:
1.Прямая заключается во
вспомогательную плоскость
ℓ⊂ П2
2.Определяется линия
пересечения заданной
плоскости со вспомогательной
= k
3.Отмечается искомая
точка на пересечении
данной прямой с линией
пересечения плоскостей
k ℓ=D

20.

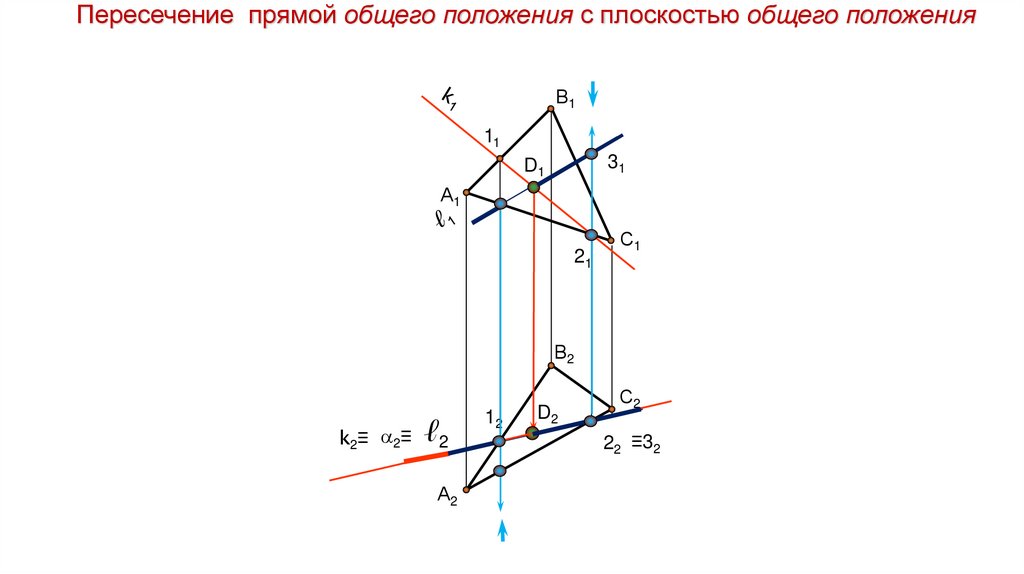
Пересечение прямой общего положения с плоскостью общего положения
В1
11
31
D1
А1
21
С1
В2
k2≡ 2≡ ℓ2
А2
12
D2
С2
22 ≡32

21.

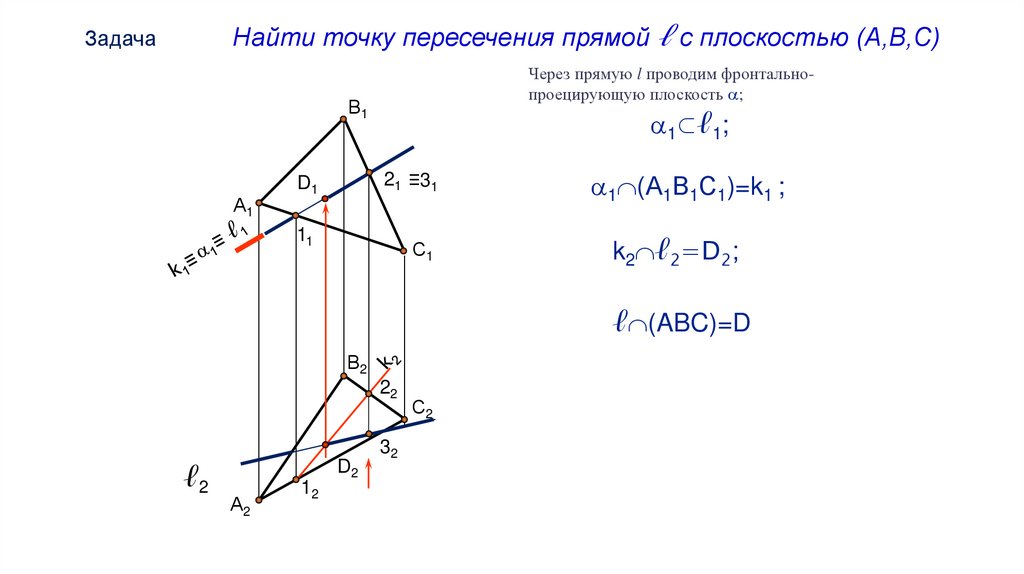
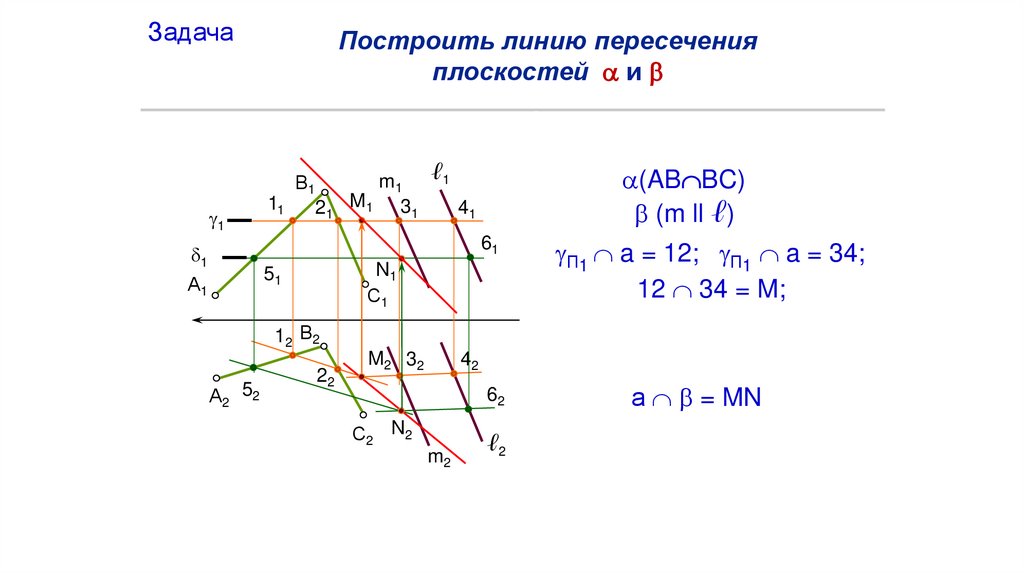
Найти точку пересечения прямой ℓ с плоскостью (А,В,С)
Задача
Через прямую l проводим фронтальнопроецирующую плоскость ;
В1
А1
D1
1⊂ℓ1;
21 ≡31
1 (А1В1С1)=k1 ;
С1
k2 ℓ2=D2;
11
ℓ (ABC)=D
В2
22
ℓ2
А2
12
D2
32
С2

22.

Пересечение прямой общего положения с плоскостью общего положения
m
l1
3
1
1
K
A1
1
1
x1
C
21
1
41=
51
B
1
1
2
A
K2 2
2
2
l2 2
l2=g2=m
12
12=3
2
B2
42
52
С2
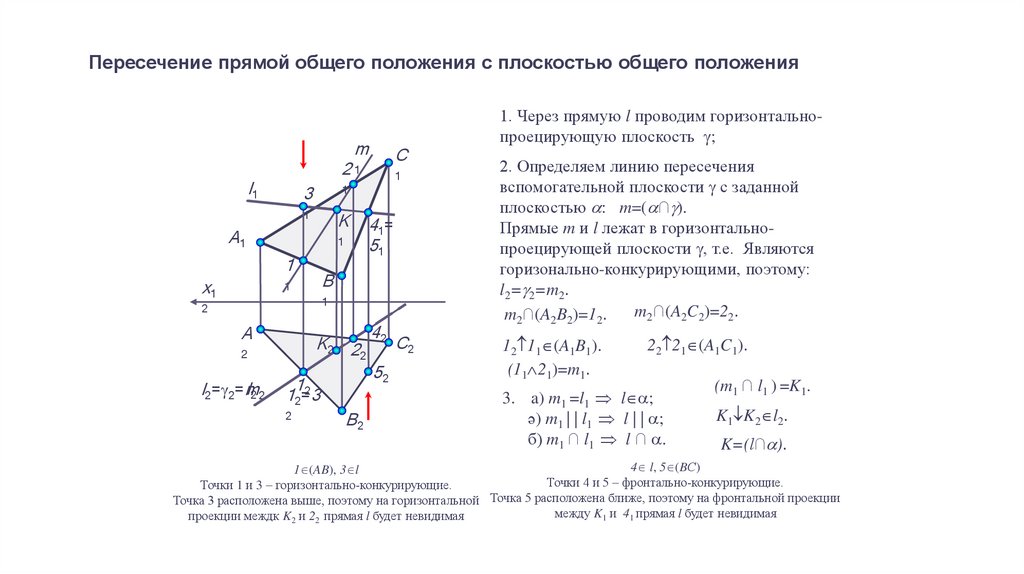
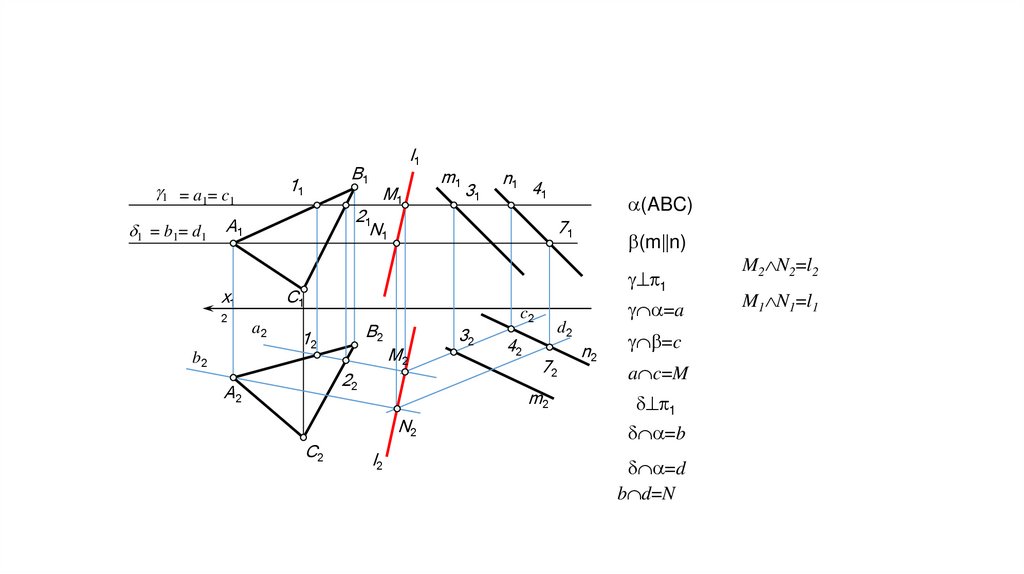
1. Через прямую l проводим горизонтальнопроецирующую плоскость g;
2. Определяем линию пересечения
вспомогательной плоскости g с заданной
плоскостью : m=( ∩g).
Прямые m и l лежат в горизонтальнопроецирующей плоскости g, т.е. Являются
горизонально-конкурирующими, поэтому:
l2=g2=m2.
m2∩(A2C2)=22.
m2∩(A2B2)=12.
12 11 (A1B1).
(11 21)=m1.
22 21 (A1C1).
3. a) m1 =l1 l ;
ә) m1 | | l1 l | | ;
б) m1 ∩ l1 l ∩ .
(m1 ∩ l1 ) =K1.
K1 K2 l2.
K=(l∩ ).
4 l, 5 (BС)
1 (AB), 3 l
Точки 4 и 5 – фронтально-конкурирующие.
Точки 1 и 3 – горизонтально-конкурирующие.
Точка
5
расположена
ближе, поэтому на фронтальной проекции
Точка 3 расположена выше, поэтому на горизонтальной
между K1 и 41 прямая l будет невидимая
проекции междк K2 и 22 прямая l будет невидимая

23.

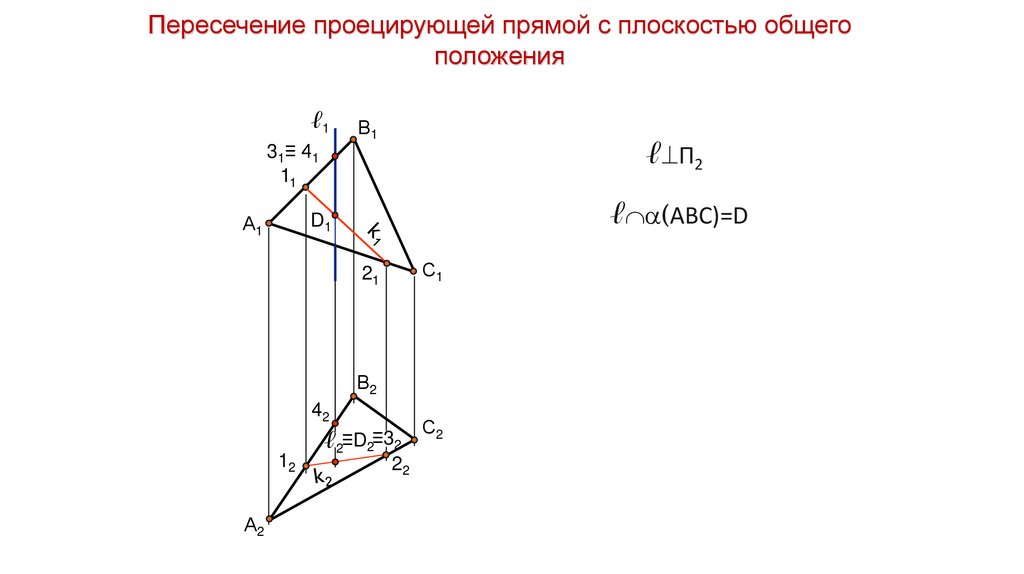
Пересечение проецирующей прямой с плоскостью общего
положения
ℓ1
31≡ 41
11
В1
ℓ П2
ℓ (АВС)=D
D1
А1
21
С1
В2
42
12
А2
ℓ2≡D2≡32
22
С2

24.

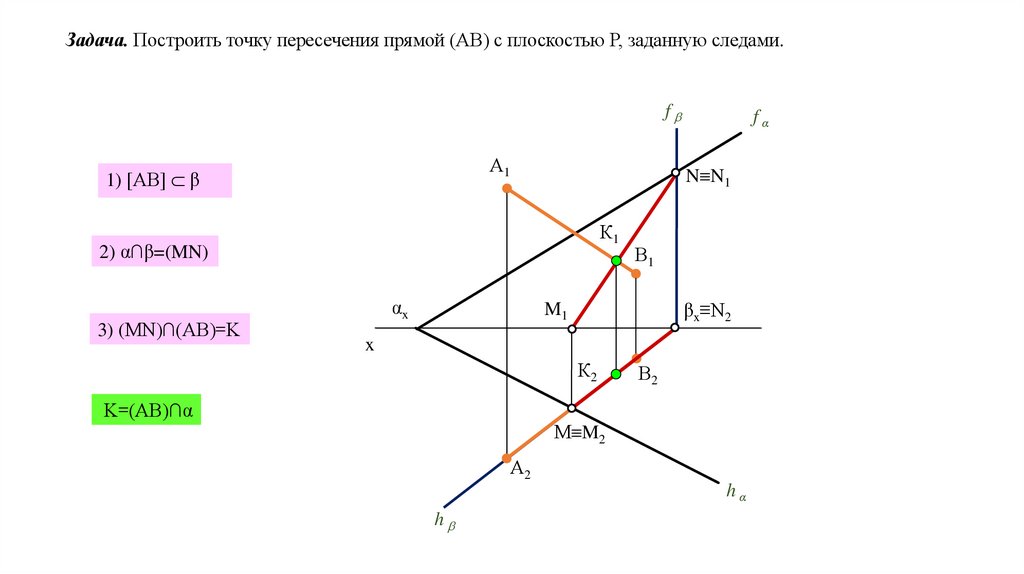
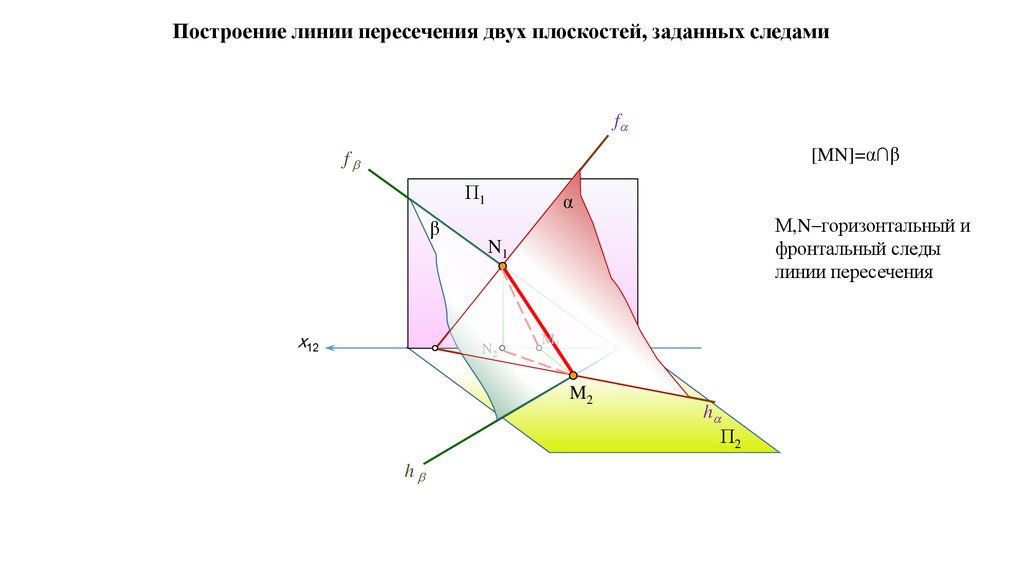
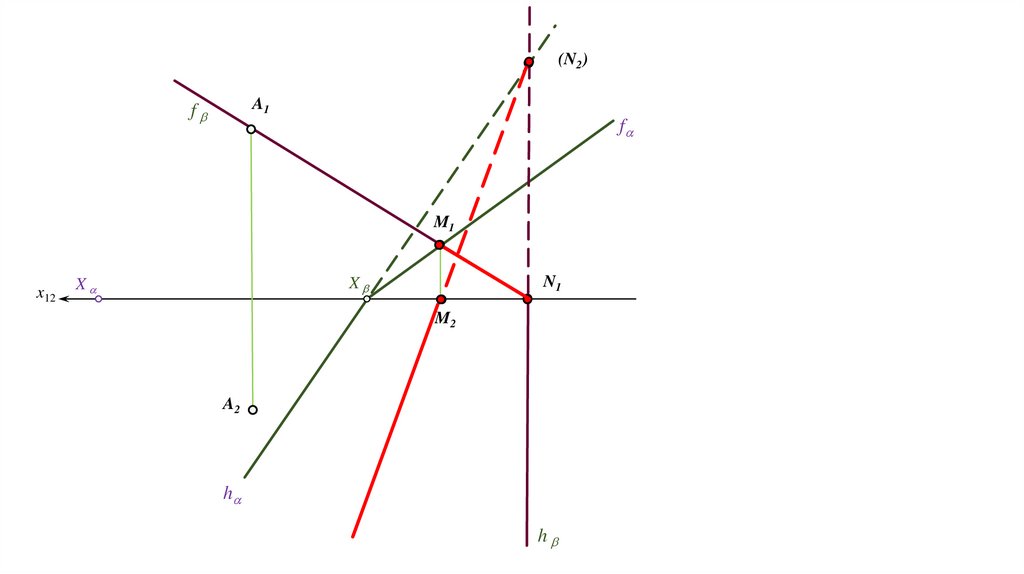
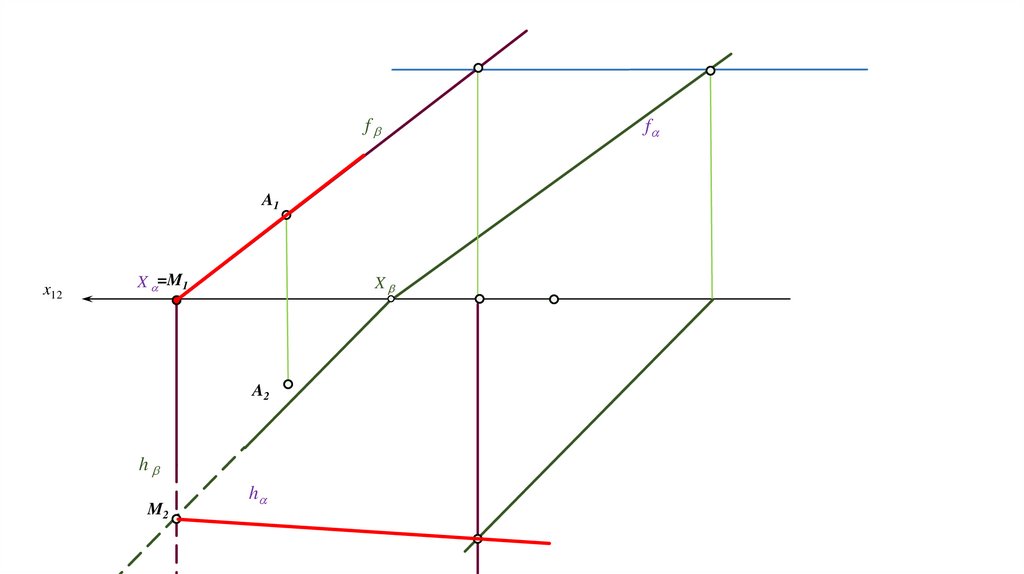
Задача. Построить точку пересечения прямой (АВ) с плоскостью Р, заданную следами.
f
А1
1) АВ β
N N1
К1
2) α∩β=(MN)
αx
3) (MN)∩(AB)=K
fα
В1
βx≡N2
M1
x
К2
В2
K=(AB)∩α
М M2
А2
hα
h

25.

6. Взаимное расположение плоскостей.
Две различные плоскости пересекаются по собственной или несобственной прямой.
Плоскости, которые пересекаются по несобственной прямой, принято называть
параллельными.
а) Параллельные плоскости. Если две пересекающиеся прямые, лежащие в одной
плоскости параллельны двум пересекающимся прямым, лежащим в другой плоскости,
то такие плоскости параллельны. Также признаком параллельности плоскостей на
эпюре является параллельность их соответствующих следов.
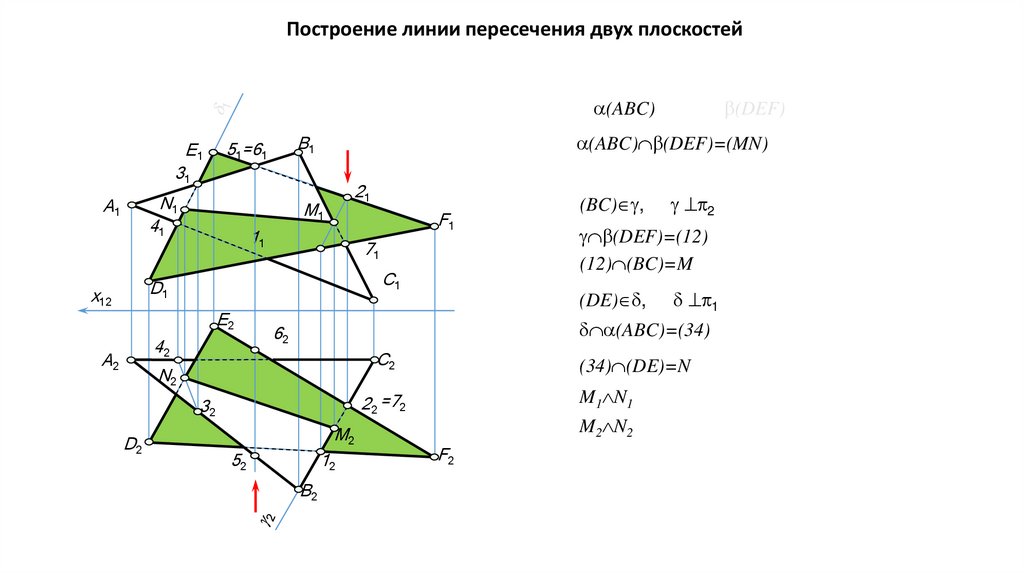
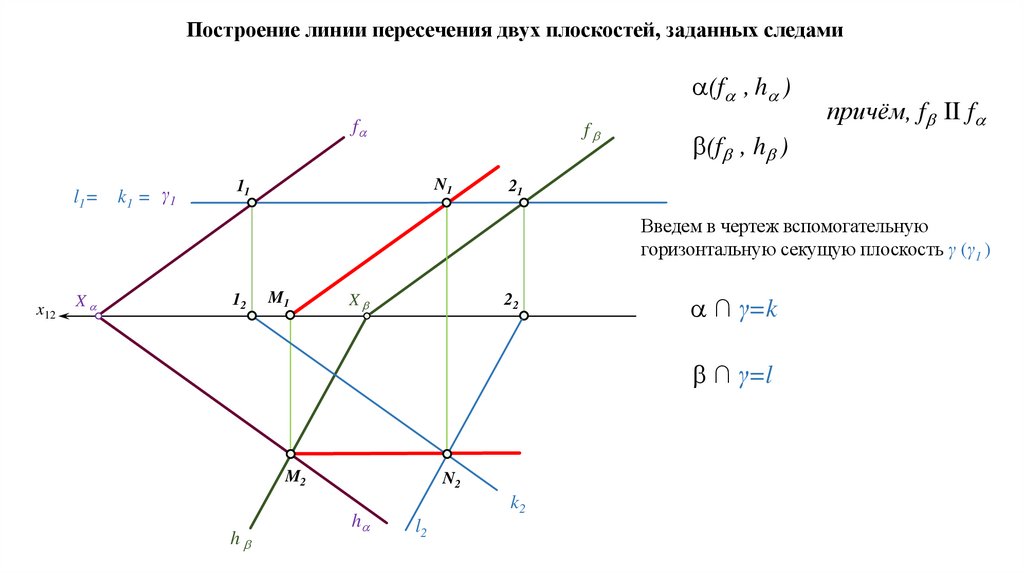
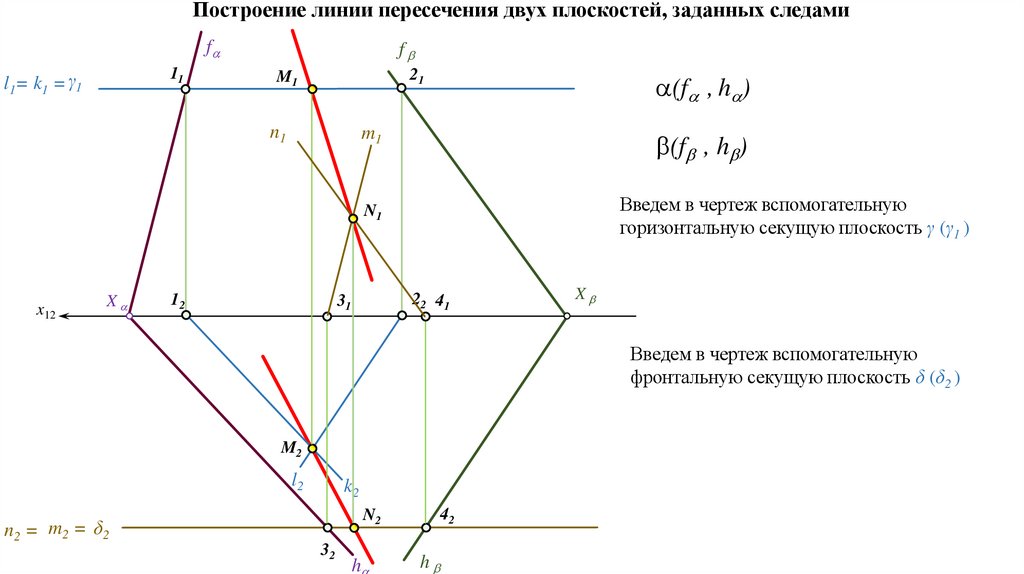
б) Пересекающиеся плоскости. Общим элементом двух пересекающихся плоскостей
является прямая, поэтому для построения линии пересечения двух плоскостей
достаточно найти две их общие точки.

26.

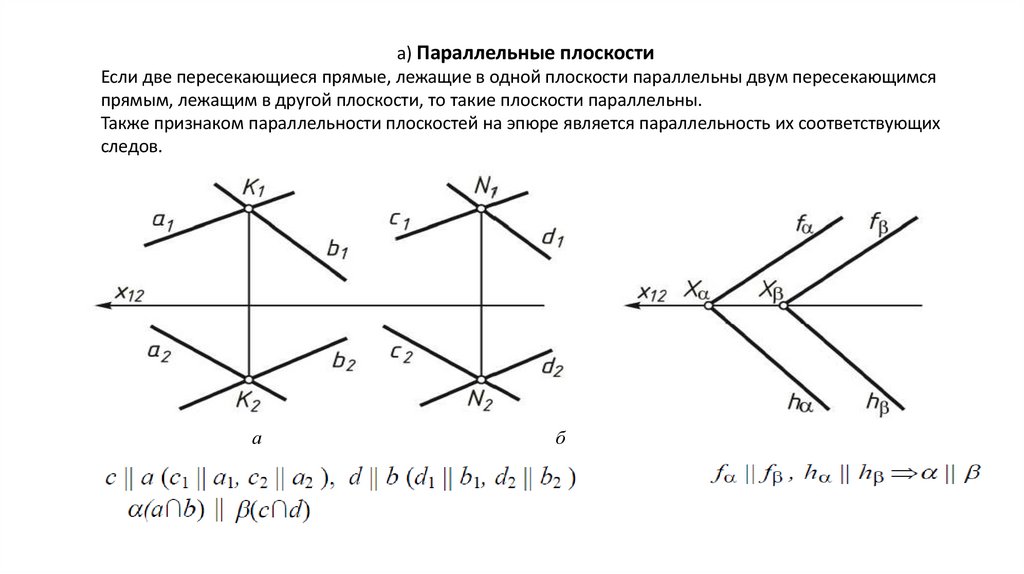
а) Параллельные плоскости
Если две пересекающиеся прямые, лежащие в одной плоскости параллельны двум пересекающимся
прямым, лежащим в другой плоскости, то такие плоскости параллельны.
Также признаком параллельности плоскостей на эпюре является параллельность их соответствующих
следов.
а
б

27.

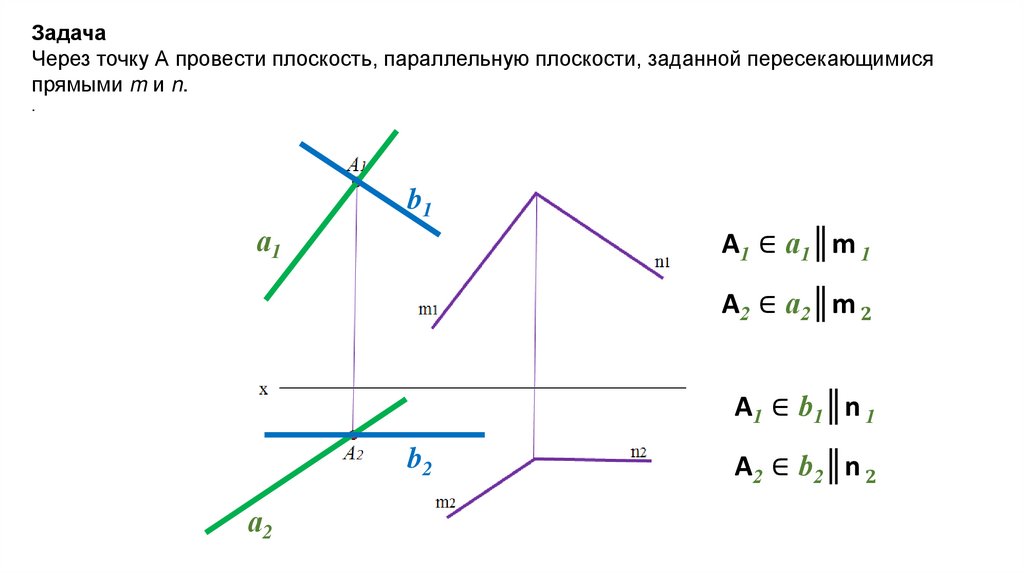
Задача
Через точку А провести плоскость, параллельную плоскости, заданной пересекающимися
прямыми m и n.
.
b1
а1
А1 ∈ a1║m 1
А2 ∈ a2║m