КИП 1 ТМ 07.10.2025 1 урок

1.

РАСЧЕТ РЕАКЦИЙ ОПОР
НАГРУЖЕННЫХ БАЛОК

2.

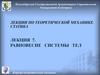
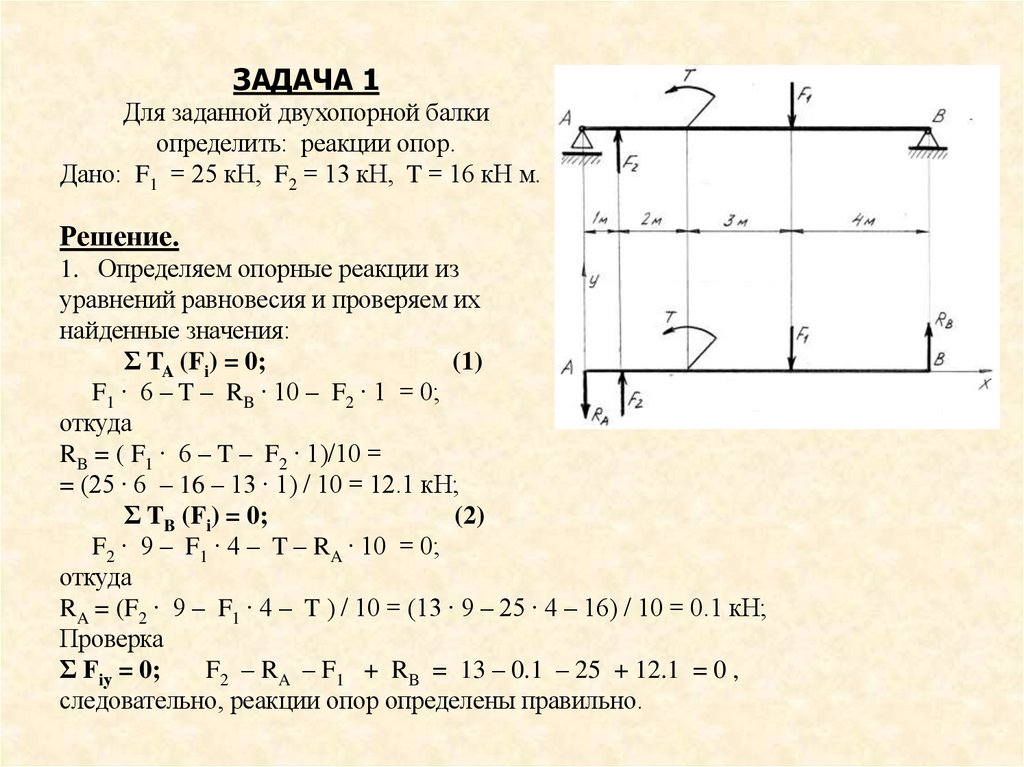
ЗАДАЧА 1
Для заданной двухопорной балки определить:
реакции опор.
Дано: F1 = 25 кН, F2 = 13 кН, T = 16 кН м.

3.

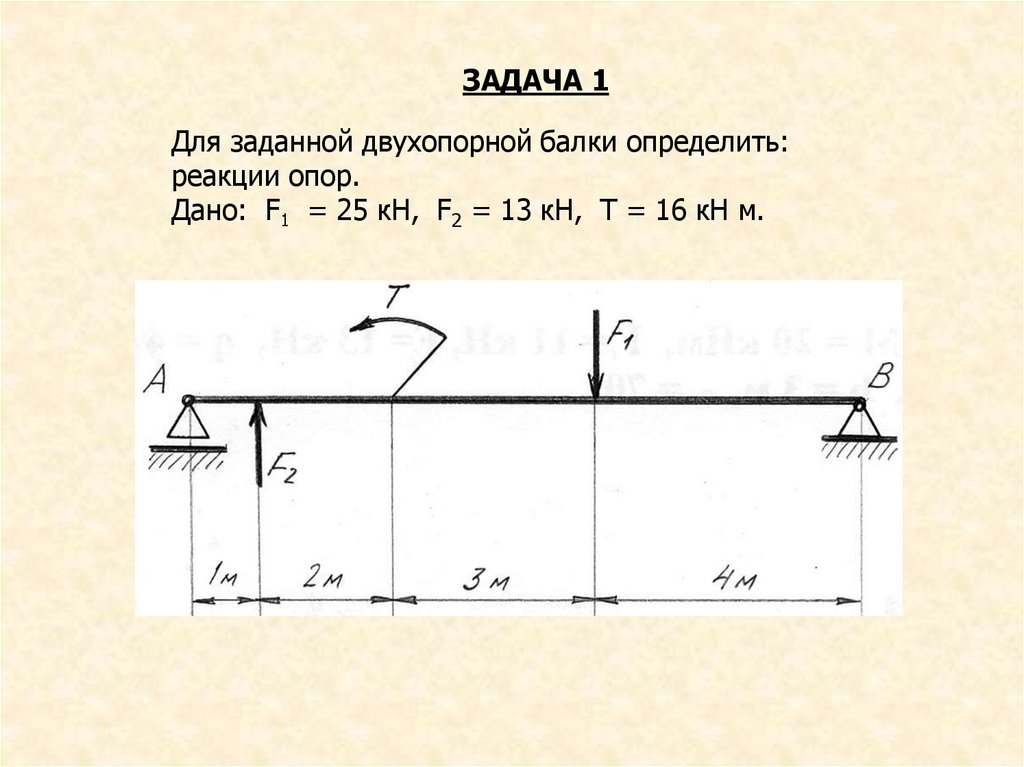
ЗАДАЧА 2
Определить реакции опор двухопорной
балки.
Дано: q = 4 Н/м; F = 35 Н; Т = 55 Н м.

4.

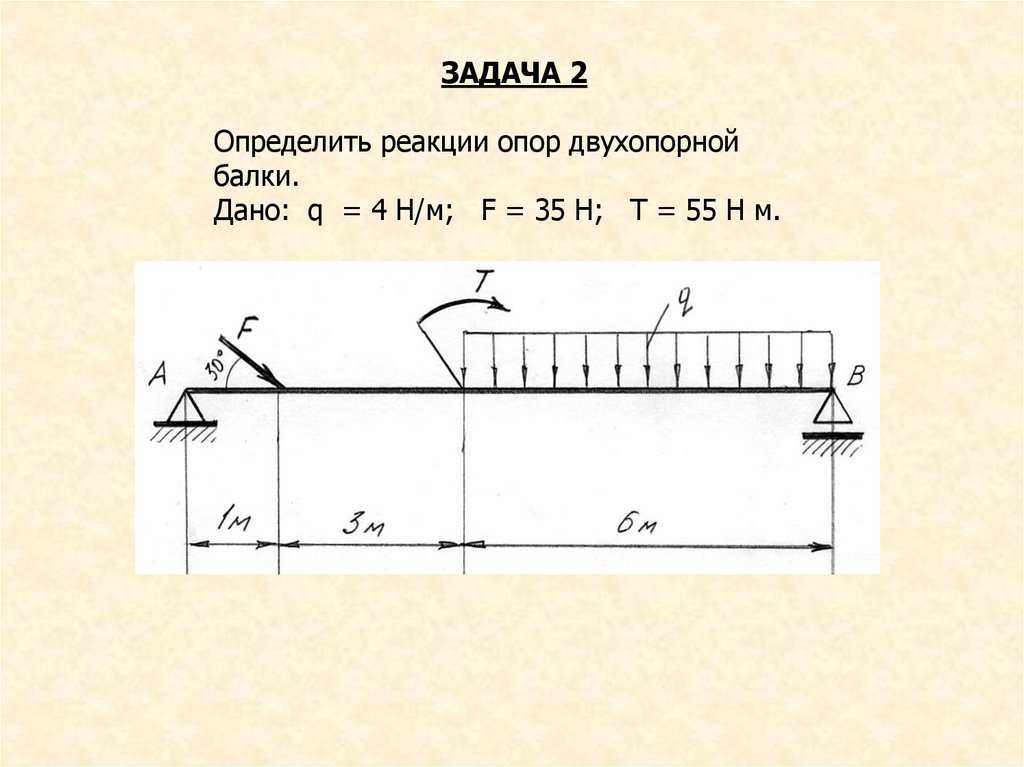
ЗАДАЧА 3
Найти реакции опор конструкции.
Дано : Т = 20 кНм, F1 = 11 кН, F2 = 13 кН, q = 4 кН/м,
а = 4 м, b = 3 м, α = 70º .

5.

ЗАДАЧА 1
Для заданной двухопорной балки
определить: реакции опор.
Дано: F1 = 25 кН, F2 = 13 кН, T = 16 кН м.
Решение.
1. Определяем опорные реакции из
уравнений равновесия и проверяем их
найденные значения:
Σ TA (Fi) = 0;
(1)
F1 ∙ 6 – T – RB ∙ 10 – F2 ∙ 1 = 0;
откуда
RB = ( F1 ∙ 6 – T – F2 ∙ 1)/10 =
= (25 ∙ 6 – 16 – 13 ∙ 1) / 10 = 12.1 кН;
Σ TB (Fi) = 0;
(2)
F2 ∙ 9 – F1 ∙ 4 – T – RA ∙ 10 = 0;
откуда
RA = (F2 ∙ 9 – F1 ∙ 4 – T ) / 10 = (13 ∙ 9 – 25 ∙ 4 – 16) / 10 = 0.1 кН;
Проверка
Σ Fiу = 0;
F2 – RA – F1 + RB = 13 – 0.1 – 25 + 12.1 = 0 ,
следовательно, реакции опор определены правильно.

6.

ЗАДАЧА 2
Определить реакции опор двухопорной балки.
Дано: q = 4 Н / м; F = 35 Н; Т = 55 Н м.
Решение.
1. Рассмотрим систему уравновешенных сил, приложенных к балке АВ.
2. Отбрасываем связи, заменяя их действие на балку реакциями. Так как направление
реакции шарнирно-неподвижноой опоры А неизвестно, то определяем ее
составляющие RAx и RAy; равномерно-распределенную нагрузку интенсивностью q
заменяем сосредоточенной силой
Fq = q 6 = 4 ∙ 6 = 24 Н.

7.

3. Для плоской системы сил, приложенных к балке, составляем три уравнения
равновесия:
Σ Fix = 0; (1)
F ∙ cos 30º – RAx = 0;
Σ Fiу = 0;
(2)
RAy – F ∙ 30º – Fq + RB = 0;
Σ TA (Fi) = 0; (3)
– RB (1 + 3 + 6) + F ∙ 1 ∙ sin 30º + Fq ∙ (0.5 ∙ 6 + 3 + 1) + T = 0.
Из (1)
RAx = F ∙ cos 30º = 35 ∙ 0.866 = 30.31 Н.
Из (2)
RAy = F ∙ sin 30º + Fq – RB = 35 ∙ 0.5 + 24 – 24.05 = 17.45 Н.
Из (3) )
RB = [F ∙ 1 ∙ sin 30º + Fq ∙ (0.5 ∙ 6 + 3 + 1) + T ] / (1 + 3 + 6) =
= (35 ∙ 1 ∙ 0.5 + 24 ∙ 7 + 55 ) / 10 = 24.05 Н.
Для проверки правильности решения воспользуемся уравнением моментов
относительно В:
Σ TВ (Fi) = 0;
RAy (1 + 3 + 6) + T – Fq ∙ 0.5 ∙ 6 – F ∙ (3 + 6) ∙ sin 30º =
= 17.45 ∙ 10 + 55 – 24 ∙ 3 – 35 ∙ 9 ∙ 0.5 = 0,
следовательно, задача решена правильно.

8.

ЗАДАЧА 3
Найти реакции опор конструкции.
Дано : Т = 20 кНм, F1 = 11 кН,
F2 = 13 кН, q = 4 кН/м,
а = 4 м, b = 3 м, α = 70º .
Решение.
1. Рассмотрим систему уравновешенных сил, приложенных к балке
АВ.
2. Отбрасываем связи : неподвижную опору А и нить.
3. Действие связей на балку заменяем реакциями.
4. Со стороны опоры А, осуществленной в виде заделки, на балку
действует реакция RА неизвестного направления, разложенная на
составляющие RА х и RАу, и пара с моментом ТА, препятствующая
вращению балки вокруг точки А, которое было бы возможным при
наличии в этой точке шарнира. Модуль реакции нити S равна F2.
Равномерно – распределенную нагрузку интенсивностью q заменяем
сосредоточенной силой
Fq = q b = 4 ∙ 3 = 12 кН.

9.

5. Для плоской системы сил, приложенных к балке, составляем уравнения
равновесия
Σ TA (Fi) = 0;
TA − T – F1 a + S (а + b) sin 70º − Fq (0.5 b + a) = 0;
(1)
Σ Fix = 0;
S cos 70º − RAx = 0;
(2)
Σ Fiу = 0;
RАу - Fq – F1 S sin 70º = 0;
(3)
Из (1)
TA = T + F1 a – S (а + b) sin 70º + Fq (0.5 b + a) =
= 20 + 13 ∙ 4 – 11 (4 + 3) 0.9397 + 12 (0.5 ∙ 3 + 4) = 65.64 кН м.
Из (2)
RAx = S cos 70º = 11 ∙ 0.34202 = 3.76 кН.
Из (3)
RAу = Fq + F1 – S sin 70º = 12 + 13 – 11 ∙ 0.9397 = 14.66 кН.
Для проверки правильности решения составим еще одно уравнение :
Σ TВ (Fi) = 0;
TA − T – RAy (а + b) + Fq 0.5 b + F1 b =
= 65.64 − 20 – 14.66 (4 + 3) + 12 ∙ 0.5 ∙ 3 + 13 ∙ 3 = 0,
следовательно, реакции опоры А найдены верно.