Вебинар 1

1. Вебинар 1

open-college.ru

2.

3. Вводное занятие. Лекция 1. Прямые и плоскости в пространстве. Лекция 2. Координаты и векторы в пространстве

open-college.ru

4.

Стереометрия – греческое слово,
составленное из «стерео» – тело
и «метрео» – измеряю.
Таким образом, стереометрия –
это «теломерие».
В стереометрии изучаются
свойства фигур в пространстве,
то есть, не лежащих в одной
плоскости. Чаще их называют
пространственными.

5.

Взаимное
расположение прямых
и плоскостей

6. Аксиомы стереометрии

Аксиома – утверждение, принимаемое без
доказательства.
А1:Через любые три точки, не лежащие на одной
прямой, проходит плоскость и притом только одна.
А2: Если две точки прямой лежат в плоскости, то
все точки прямой лежат в этой плоскости.
А3: Если две плоскости имеют общую точку, то они
имеют общую прямую, на которой лежат все общие
точки этих плоскостей.

7. Теоремы стереометрии (следствия из аксиом)

Т 1. Через прямую и не лежащую на ней точку
проходит плоскость, и притом только одна.
Т 2. Через две параллельные прямые
проходит плоскость, и притом только одна.
Т 3. Через две пересекающиеся прямые
проходит плоскость, и притом только одна.

8. Взаимное расположение прямых в пространстве

Способы взаимного расположения
прямых в пространстве:
•1.Параллельные прямые
•2.Пересекающиеся прямые
•3.Скрещивающиеся прямые

9. Определение параллельных прямых

•1) Параллельными называют прямые,
которые лежат в одной плоскости и не имеют
общих точек

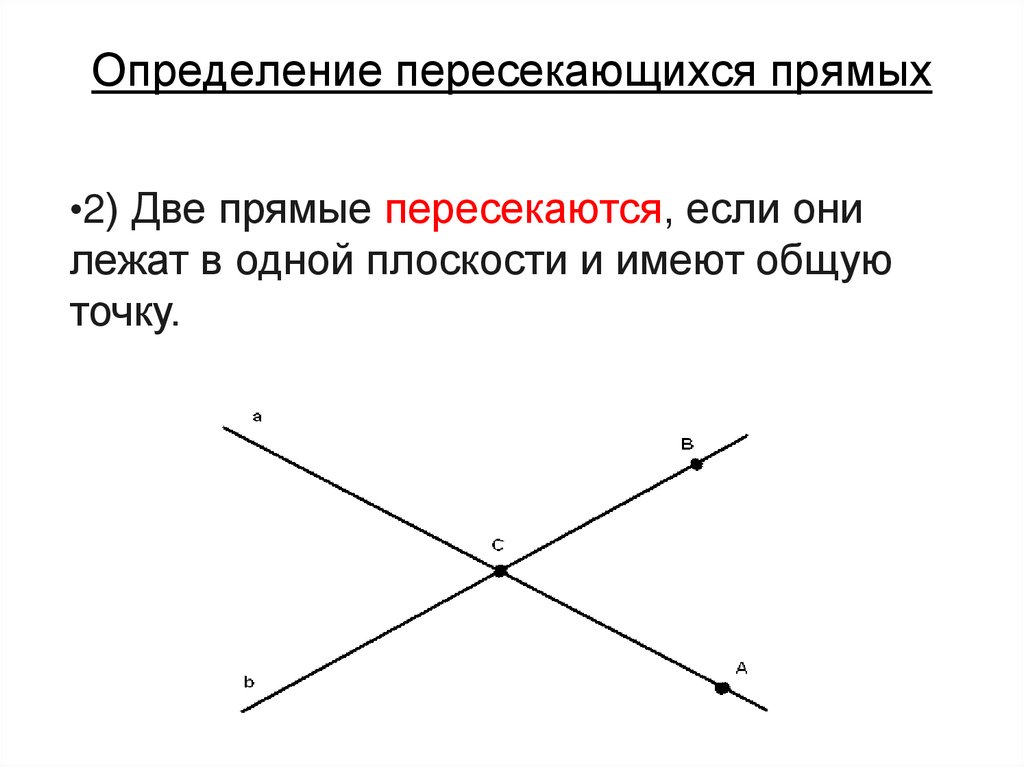
10. Определение пересекающихся прямых

•2) Две прямые пересекаются, если они
лежат в одной плоскости и имеют общую
точку.

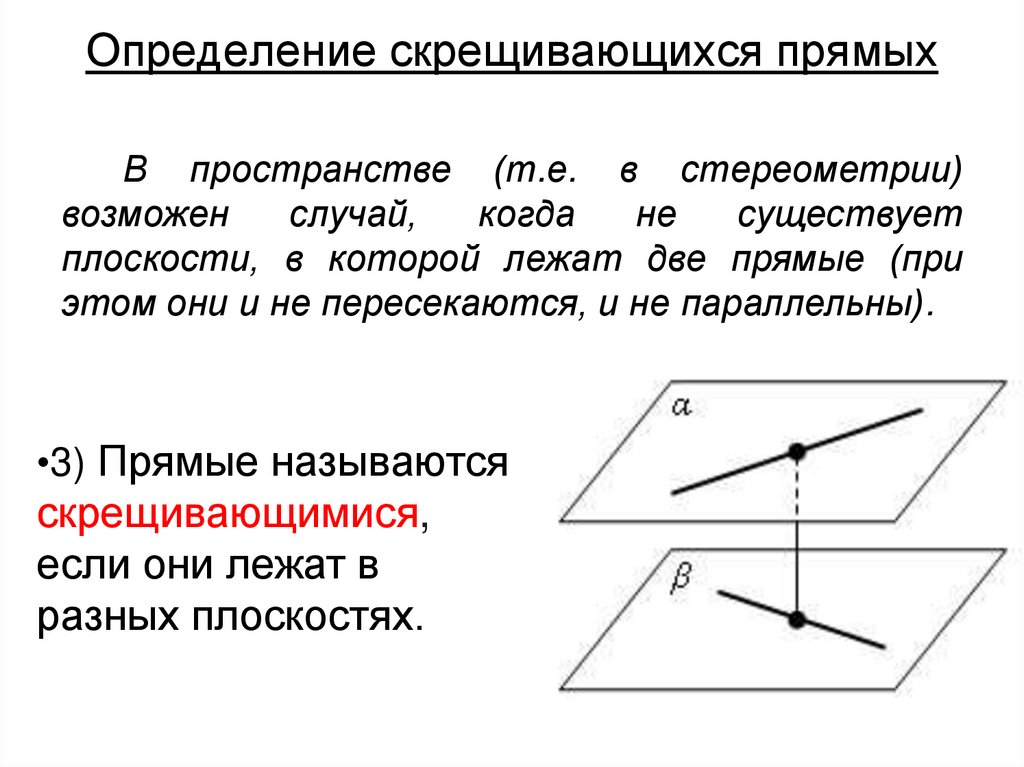
11. Определение скрещивающихся прямых

В пространстве (т.е. в стереометрии)
возможен
случай,
когда
не
существует
плоскости, в которой лежат две прямые (при
этом они и не пересекаются, и не параллельны).
•3) Прямые называются
скрещивающимися,
если они лежат в
разных плоскостях.

12. Перпендикулярность двух прямых

Определение:
Две
прямые
называются
взаимно
перпендикулярными
(перпендикулярными),
если угол между ними равен 90°.
Перпендикулярными
могут
быть
как
скрещивающиеся прямые, так и прямые лежащие и
пересекающиеся в одной плоскости.
Если прямая a перпендикулярна прямой b, то
пишут:

13.

Координаты и векторы
в
пространстве

14.

Вспомним, как определяется координатная(числовая) прямая.
1) Изображаем произвольную прямую;
2) Придаем ей положительное направление и обозначаем её;
3) Выбираем произвольную точку за начало отсчета;
4) Определяем длину единичного отрезка (масштаб).
М
0
1
х
а
Тогда любой точки этой координатной прямой соответствует единственное
действительное число a. И наоборот, любое действительное число может быть
изображено единственной соответствующей точкой, для которой это число
является координатой. Записывают: M(a).

15.

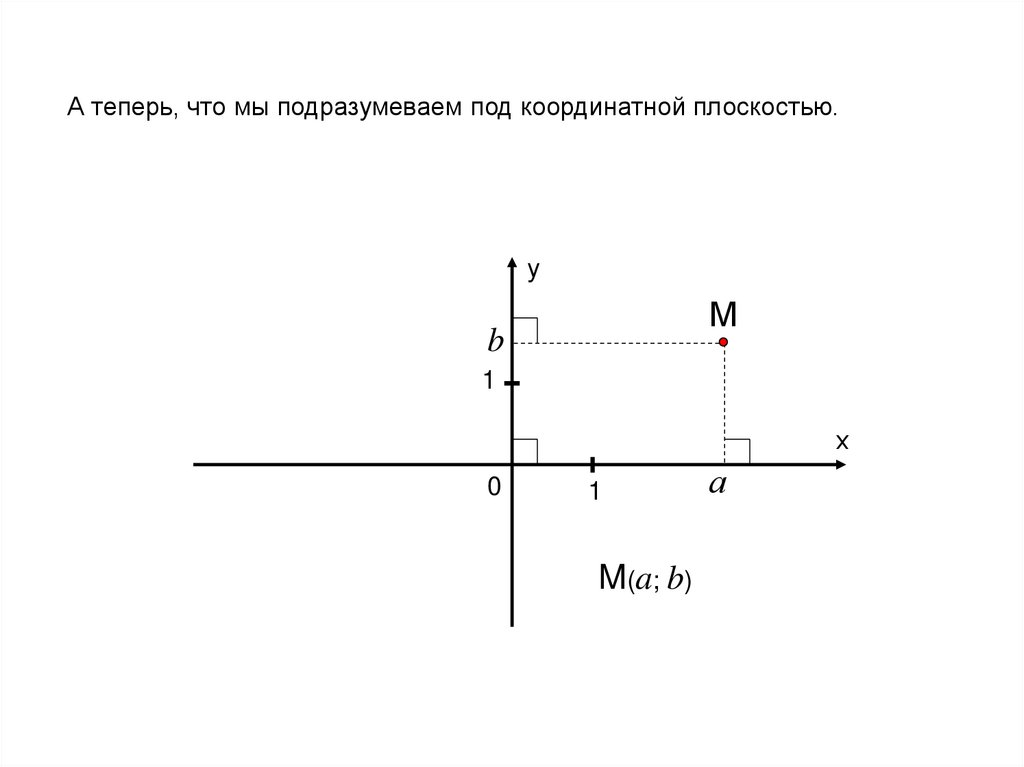
А теперь, что мы подразумеваем под координатной плоскостью.
у
М
b
1
х
0
1
M(a; b)
а

16.

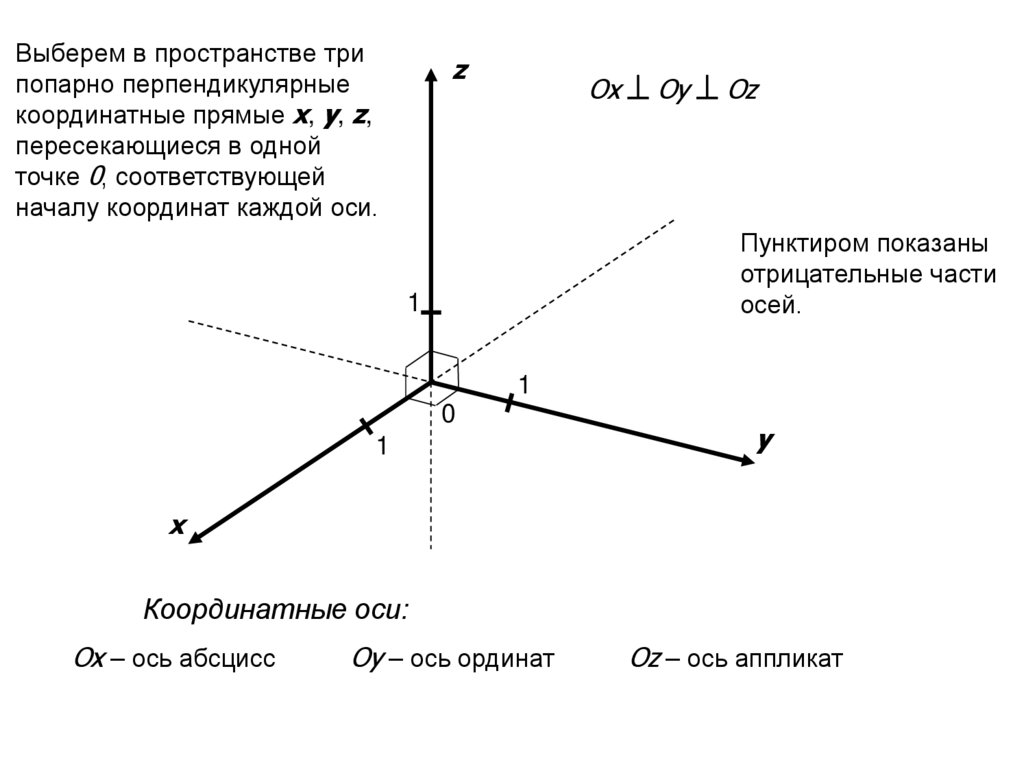
Выберем в пространстве три
попарно перпендикулярные
координатные прямые x, y, z,
пересекающиеся в одной
точке 0, соответствующей
началу координат каждой оси.
z
Ox Oy Oz
Пунктиром показаны
отрицательные части
осей.
1
1
0
1
y
x
Координатные оси:
Ox – ось абсцисс
Oy – ось ординат
Oz – ось аппликат

17.

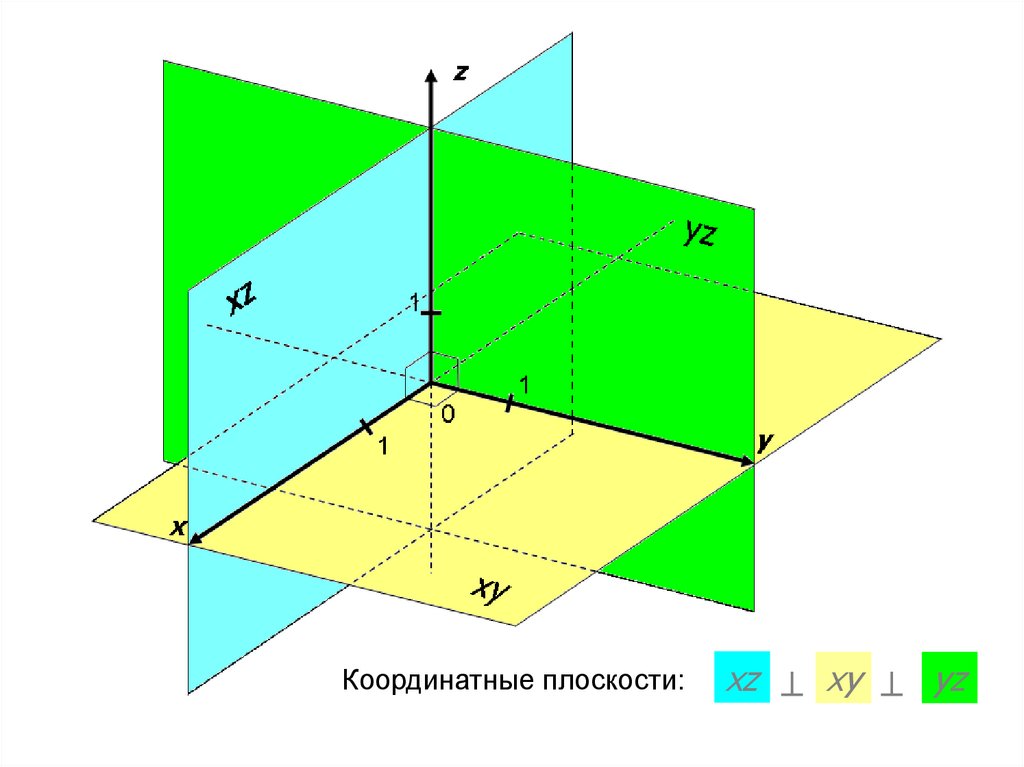
Координатные плоскости:
xz xy yz

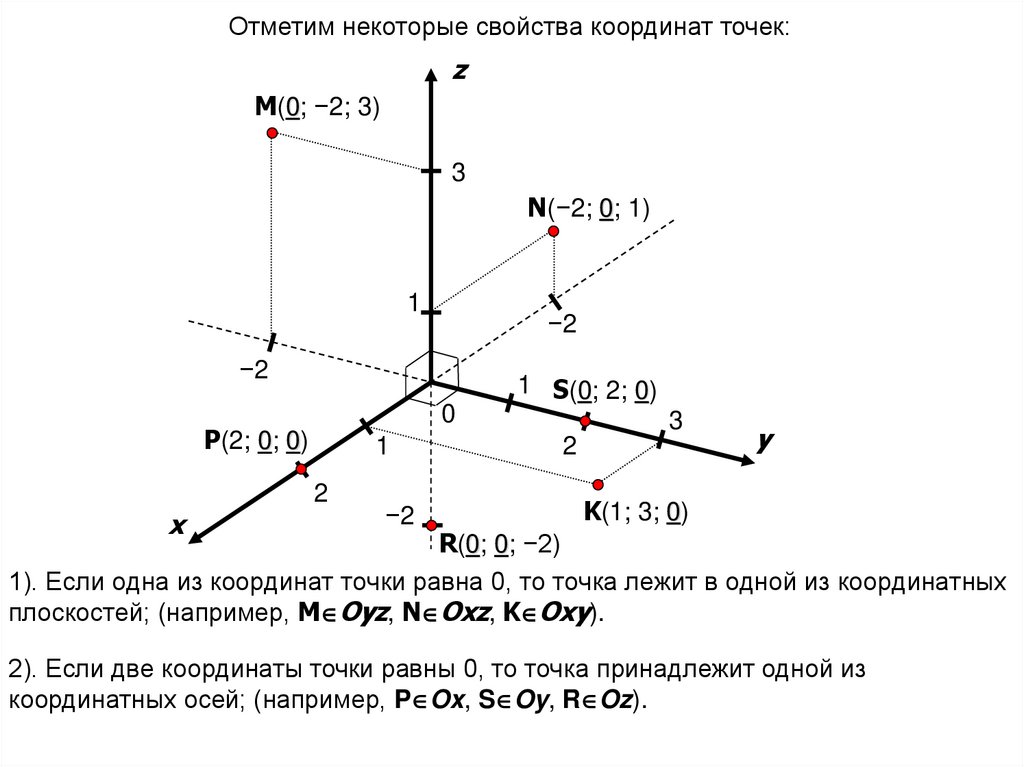
18. 1). Если одна из координат точки равна 0, то точка лежит в одной из координатных плоскостей; (например, MOyz, NOxz, KOxy).

Отметим некоторые свойства координат точек:
z
M(0; −2; 3)
3
N(−2; 0; 1)
1
−2
−2
1 S(0; 2; 0)
0
P(2; 0; 0)
1
2
x
−2
3
2
y
K(1; 3; 0)
R(0; 0; −2)
1). Если одна из координат точки равна 0, то точка лежит в одной из координатных
плоскостей; (например, M Oyz, N Oxz, K Oxy).
2). Если две координаты точки равны 0, то точка принадлежит одной из
координатных осей; (например, P Ox, S Oy, R Oz).

19. Формулы середины отрезка и расстояния между точками на плоскости.

x1 x2 y1 y2
М
;
2
2
АВ
x2 x1 y2 y1
2
2

20. о

Пример 1
о
Дано: А (3;-1), В (-2;4),
точка М – середина АВ.
Найти: IАВI, М(x;y).
Решение:
АВ
x2 x1 2 y2 y1 2
АВ
2 3 2 4 ( 1) 2
25 25
50 5 2
Пример 2
Дано: А (3;4), В (2;-1),
точка С – середина АВ.
Найти: IАВI, С(x;y).
Решение:
АВ
x2 x1 2 y2 y1 2
АВ (2 3) 2 ( 1 4) 2 1 25 26
x x2 y1 y 2
М 1
;
2
2
x x2 y1 y 2
С 1
;
2
2
3 ( 2) 1 4
М
;
2
2
3 2 4 ( 1)
С
;
2
2
М 0,5;1,5
Ответ:
АВ 5 2
М 0,5;1,5
С 2,5;1,5
Ответ: АВ
26
С 2,5;1,5

21. Задача Найдите координаты середины отрезка АВ и длину отрезка АВ, если:

1 А (3;-1), В (-2;4)
2 А (3;4), В (2; -1)

22. Пример:

А (4;-2), В (-3;6)

23.

Расстояние между точками A(x1; y1; z1) и B(x2; y2; z2)
АВ
x2 x1 y2 y1 z2 z1
2
2
2
Координаты середины отрезка АВ, где A(x1; y1; z1) и B(x2; y2; z2)
x1 x2 y1 y2 z1 z2
M
;
;
2
2
2

24. Задача

Дано:
А (1;-1;2), В (3;1;-2)
Найдите координаты середины отрезка АВ и
его длину.

25. Задача

Дано:
А (3;-1;4), В (2;1;-6)
Найдите координаты середины отрезка АВ и его
длину.

26.

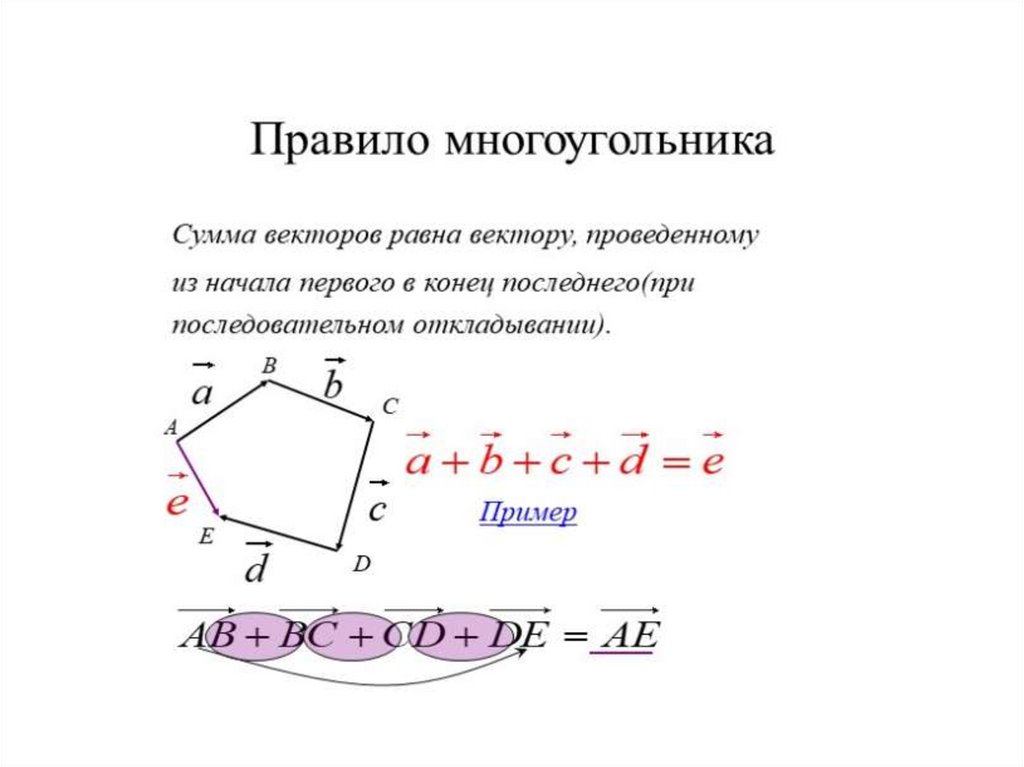
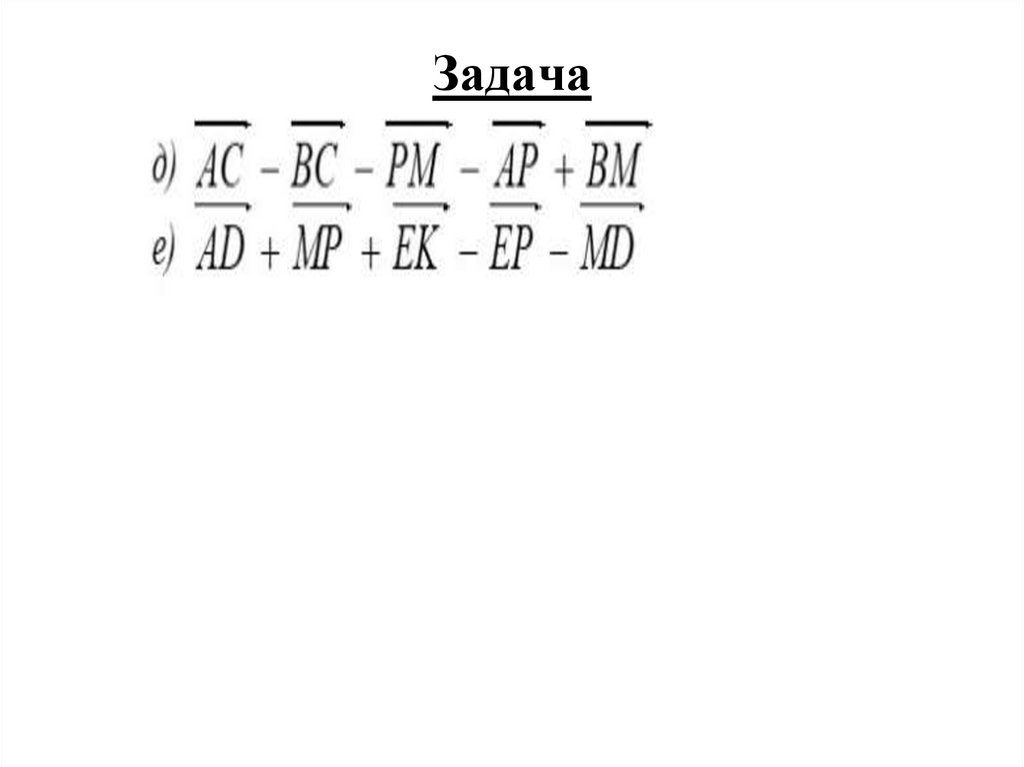
Векторы в
пространстве

27.

28.

29.

30.

31.

32.

33.

34.

35.

36.

37.

38.

39. Задача

40. Задача

41. Спасибо!

open-college.ru