Похожие презентации:
свойства квадратных корней
1. «Свойства квадратных корней».
√ «Свойстваквадратных
корней».
a
2.
1. Найдите значение выражения81 4 324 18
81 4 9 2 18
81 4
81 4
Вывод:
Если а ≥ 0, b ≥ 0, то a b a b
Корень из произведения неотрицательных
множителей равен произведению корней из этих
множителей
3.
Если а ≥ 0, b ≥ 0, то a b a b64 0,04 64 0,04 8 0, 2 1,6
Решите самостоятельно
36 0,25 36 0, 25 6 0 ,5 3
121 0,49 121 0,49 11 0 ,7 7,7
9 64 0 , 25 9 64 0, 25 3 8 0 ,5 12
0,36 144 2,25 0,36 144 2,25 0 ,6 12 1,5 10,8
4.
2. Найдите значение выражения6
36
169 13
Выво
д:
6
169 13
36
36
169
Если а ≥ 0, b > 0, то
36
169
a
b
a
b
Корень из дроби, числитель которой неотрицателен,
а знаменатель положителен, равен корню из
числителя, деленному на корень из знаменателя
5.
Если а ≥ 0, b > 0, тоa
b
a
b
Решите самостоятельно
9
81
81
196
196 14
9
25
1
16
16
1
5
1
4
16 4
25
25 16 196
25 16 196 5 4 14 40 13
1
81 49 9
81 49
9 9 7 3 27 27
6.
05.12.20256
7.
a 0, ( a ) a2
a a
2
05.12.2025
7
8. Карточка – памятка «Свойства арифметического квадратного корня».
ab
a
b
1
a
a
2 b
b
3
a2 a
4
a 2b a b
a 0,b 0
a 0,b 0
a 0,b 0
9.
05.12.20259
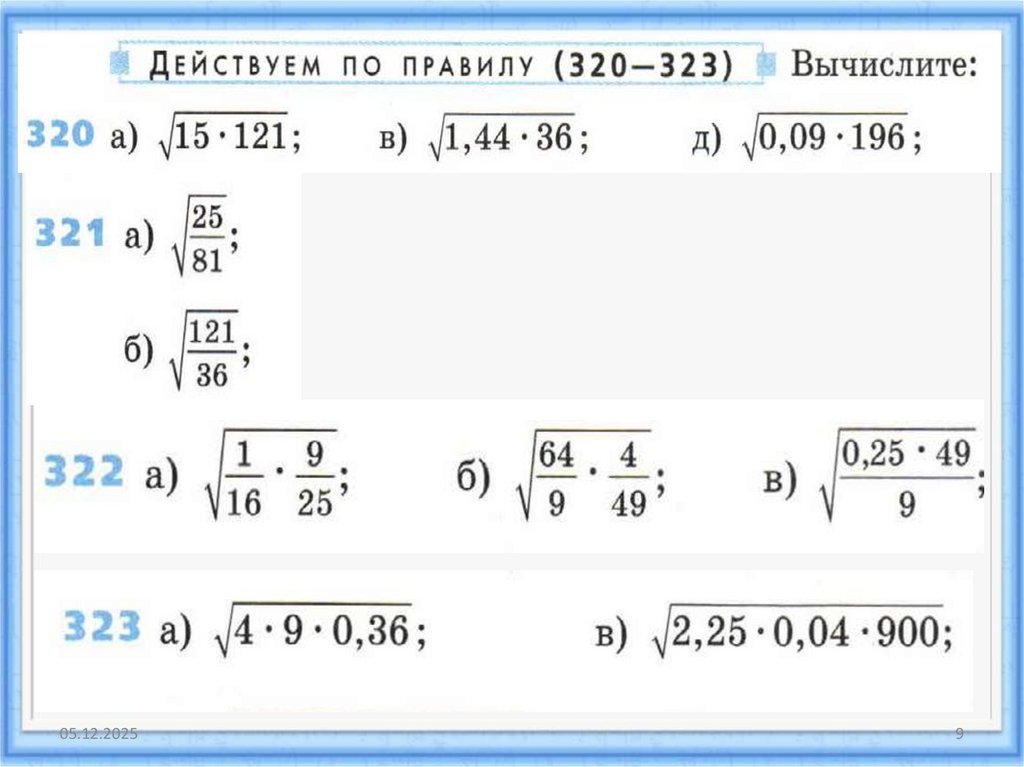
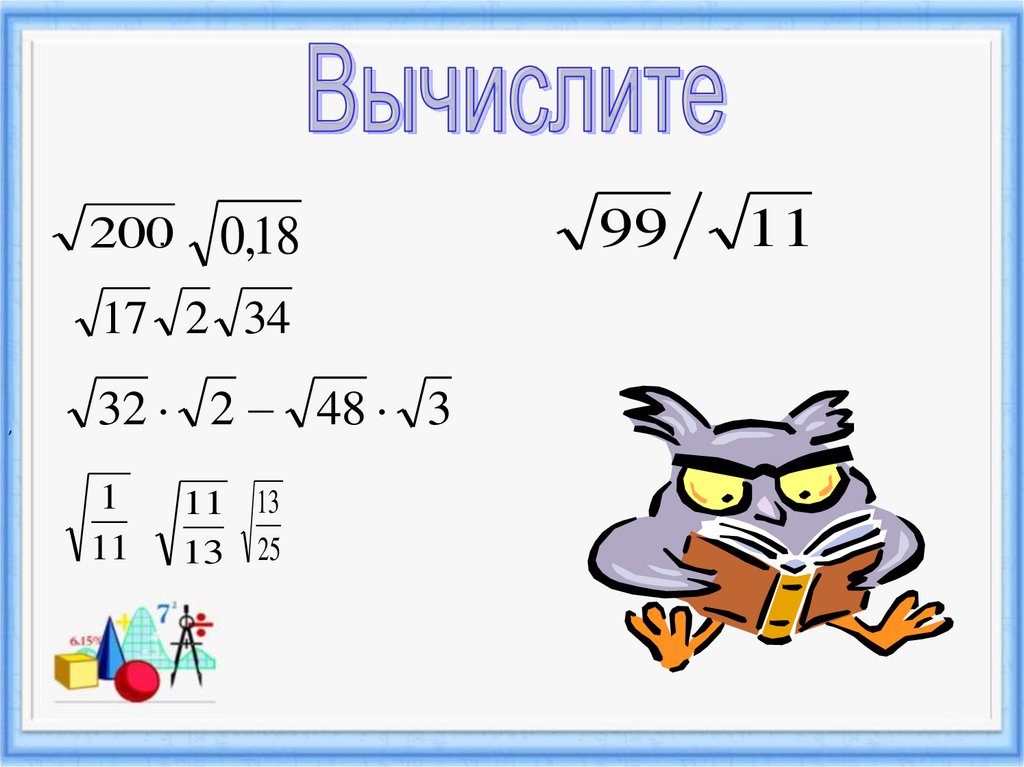
10. Вычислите:
11.
2000,18
17 2 34
,
32 2 48 3
1
11
11 13
13 25
99
11









 Математика
Математика








