Метод Эйлера и Рунге-Кутта

1. Понятие о дифференциальном уравнении. Метод Эйлера и Рунге-Кутта

2. Дифференциальное уравнение-

Дифференциальное уравнениеЭто уравнение, в котором неизвестная
функция входит под знаком производной
или дифференциала.
Например:
dy
d y
z z
2( y 3);
t 1;
2 0;
2
2
dx
dt
x
y
2
2
2

3. Порядок дифференциального уравнения-

Порядок дифференциального
уравненияЭто наивысший порядок производной
(или дифференциала), входящей в
уравнение .
Например: уравнения
2
2
2
d
s
z
z
2-го порядка,
t 1;
1
x 2
dt 2
dy 2
( x y )dx ( x y )dy 0 1-ого порядка.
2
2
2
2

4. Обыкновенное дифференциальное уравнение

Это дифференциальное уравнение, в
котором неизвестная функция, входящая
в уравнение, зависит только от одной
независимой переменой. Например:
2
d y
x 2 2; 2 s dt t ds.
dx
2

5. Параметры дифференциального уравнения

Обыкновенное дифференциальное
уравнение n-го порядка в самом общем
случае содержит независимую переменную
x , неизвестную функцию y и ее
производные или дифференциалы до n-го
порядка включительно и имеет вид
F ( x, y, y' , y' ' ,..., y ) 0
(n)

6. Решение дифференциального уравнения-

Решение дифференциального
уравненияЭто всякая дифференцируемая функция
y (x), удовлетворяющая этому
уравнению, т.е. такая, после подстановки
которой в уравнение y ( n) f ( x, y, y' , y' ' ,..., y ( n 1) )
оно обращается в тождество.

7. Задача Коши-

Задача КошиНайти решение y (x) уравнения
y ( n ) f ( x, y, y' , y' ' ,..., y ( n 1) ),
удовлетворяющее
дополнительным условиям, состоящим в том, что
решение должно принимать вместе со своими
производными до (n-1)-го порядка заданные числовые
( n 1)
значения y0 , y0 , y0 ,..., y0
при заданном числовом
значении независимой переменной x:
( n 1)
( n 1)
y y0 , y ' y0 , y ' ' y0 ,..., y
y0
при
x x0 .

8. Решение дифференциальных уравнений численными методами

Методы приближенного решения
дифференциальных уравнений
Аналитические методы
Численные методы
дают приближенное
решение
дифференциального
уравнения в виде
аналитического выражения
дают приближенное
решение
дифференциального
уравнения в виде
таблицы

9. Решить дифференциальное уравнение численным методом -

Решить дифференциальное
уравнение численным методом это значит для
заданной
последовательности аргументов
x0,x1,…,xn и числа y0 , не
определяя функцию y=F(x) ,
найти такие значения y1,…,yn,
что yi=F(xi) и F(x0)=y0.

10. Методы численного решения дифференциальных уравнений

Метод Эйлера
Модификации метода Эйлера
Метод Рунге-Кутта
Метод Адамса

11. Метод Эйлера

12. Постановка задачи

Пусть дано обыкновенное
дифференциальное уравнение первого
порядка y`=f(x,y) с начальным условием
x=x0 , y(x0)=y0 . Требуется найти решение
уравнения y`=f(x,y) на отрезке [a,b].

13. Все вычисления по методу Эйлера удобно располагать в таблице

i
Xi
Yi
Y`i=f(Xi,Yi)
h*Y`i
0
X0
Y0
Y`0=f(X0,Y0)
h*Y`0
1
X1=X0+h
Y1=Y0+h*Y`0
Y`1=f(X1,Y1)
h*Y`1
2
X2=X1+h
Y2=Y1+h*Y`1
Y`2=f(X2,Y2)
h*Y`2
…
…
…
…
…
n
Xn=Xn-1+h Yn=Yn-1+h*Y`n-1

14. Решение дифференциального уравнения методом Эйлера

Проинтегрировать методом Эйлера
дифференциальное уравнение y`=y-x с
начальным условием y(0)=1,5 на
отрезке[0;1,5], приняв h=0,25. Вычисления
вести с четырьмя знаками после запятой.

15. Метод Рунге-Кутта

Пусть необходимо найти численное решение
уравнения y’=f(x, y), при условии, что y(x0)=y0
Идея метода состоит и в представлении
разности
Δy(x)=y(x+h)-y(x)
(1.1)
В виде суммы поправок kj с коэффициентами
рj
Δy=p1k1+ p2k2+…+ prkr ,

16. Метод Рунге-Кутта

где
k1=f(x, y),
k2=f(x+α2h, y=β21k1), …,
kr=hf(x+αrh, y=βr1k1+ βr2k2+…+ βrr-1kr-1).
Коэффициенты рj , αj , βji находят
сравнением разложений Δy и ki по
степеням h.

17. Метод Рунге-Кутта

В случае r=4 получают
k1 hf ( x, y ),
h
k
k 2 hf x , y 1
2
2
h
k2
k3 hf x , y ,
2
2
k 4 hf x h, y k3
1
y k1 2k 2 2k3 k 4
6
(1.2)
(1.3)

18. Метод Рунге-Кутта

При x=x0 с помощью формул (1.1)-(1.3)
находим
yi 1 yi yi (i 0,1,2,...)
(1.4)

19. Метод Рунге-Кутта

Где
(1.5)
Метод Рунге-Кутта
1
y k 2k 2k k
6
'
1
i
'
2
'
3
'
4
'
h
k1
'
k 2 hf ( xi , yi
2
2
'
h
k2
'
k3 hf ( xi , yi
2
2
'
'
k 4 hf ( xi h, yi k3
k hf ( xi , yi )
'
1
(1.6)

20. Метод Рунге-Кутта

Пример. Методом Ренге-Кутта найти
решение задачи Коши для уравнения y`=yx2, y(1)=0,
x [1, 2] в первых пяти точках, взяв h=0,1
Решение. Поскольку в данном примере f(x,
y)= y-x2 , и в силу условия x0 =1, y0 =0,
2
x
то f(x0 , y0 )= y0- 0 =0-1=-1.

21. Метод Рунге-Кутта

По формулам (1.6) находим
k10 hf ( x0 , y0 ) 0,1( 1) 0,1
k 20 hf (1,05; 0,05) 0,1[( 0,05) (1,05) 2 ] 0,1152
k30 hf (1,05; 0,0576) 0,1[( 0,0576) (1,05) 2 ] 0,1160
k 40 hf (1,1; 0,1160) 0,1[( 0,1160) (1,1) 2 ] 0,1326
По формуле (1.5) вычисляем
1
y0 [( 0,1) 2( 0,1152) 2( 0,1160) ( 0,1326)] 0,1158
6

22. Метод Рунге-Кутта

Значение y1 вычисляем по формуле y1 =
y0+Δy0 (см. формулу (1.4) при i=0).
y1 = 0+(-0,1158)=-0,1158
Таким образом, полученное приближенное
значение
y1 =-0,1158 при x1 =1,1

23. Метод Рунге-Кутта

C помощью формул (1.6) при i=1 найдём
приближённое значение y2 при x2 =1,1,
решив задачу Коши для того же уравнения
y`=y-x2 ,
y(1,1)=-0,1158.
Далее находим y3,y4,y5.

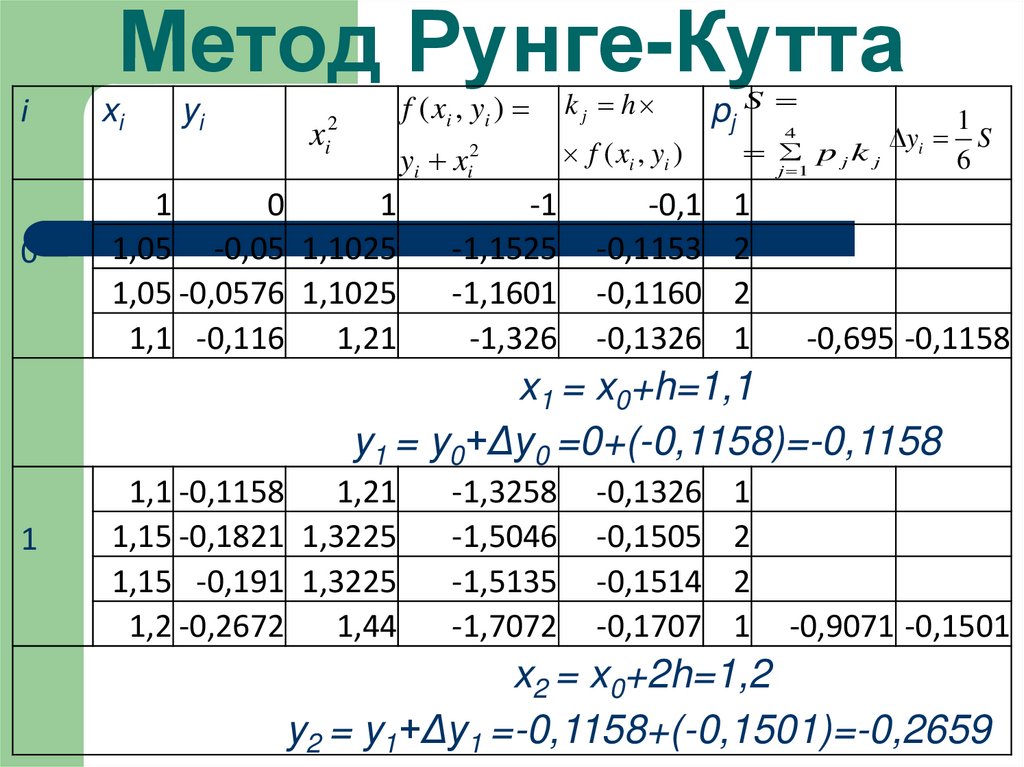
24. Метод Рунге-Кутта

i
0
xi
yi
xi2
1
0
1
1,05 -0,05 1,1025
1,05 -0,0576 1,1025
1,1 -0,116
1,21
f ( xi , yi )
k j h
yi xi2
f ( xi , yi )
-1
-1,1525
-1,1601
-1,326
-0,1
-0,1153
-0,1160
-0,1326
pj S 4
1
yi S
p jk j
6
j 1
1
2
2
1
-0,695 -0,1158
x1 = x0+h=1,1
y1 = y0+Δy0 =0+(-0,1158)=-0,1158
1
1,1 -0,1158
1,21
1,15 -0,1821 1,3225
1,15 -0,191 1,3225
1,2 -0,2672
1,44
-1,3258
-1,5046
-1,5135
-1,7072
-0,1326
-0,1505
-0,1514
-0,1707
1
2
2
1
-0,9071 -0,1501
x2 = x0+2h=1,2
y2 = y1+Δy1 =-0,1158+(-0,1501)=-0,2659

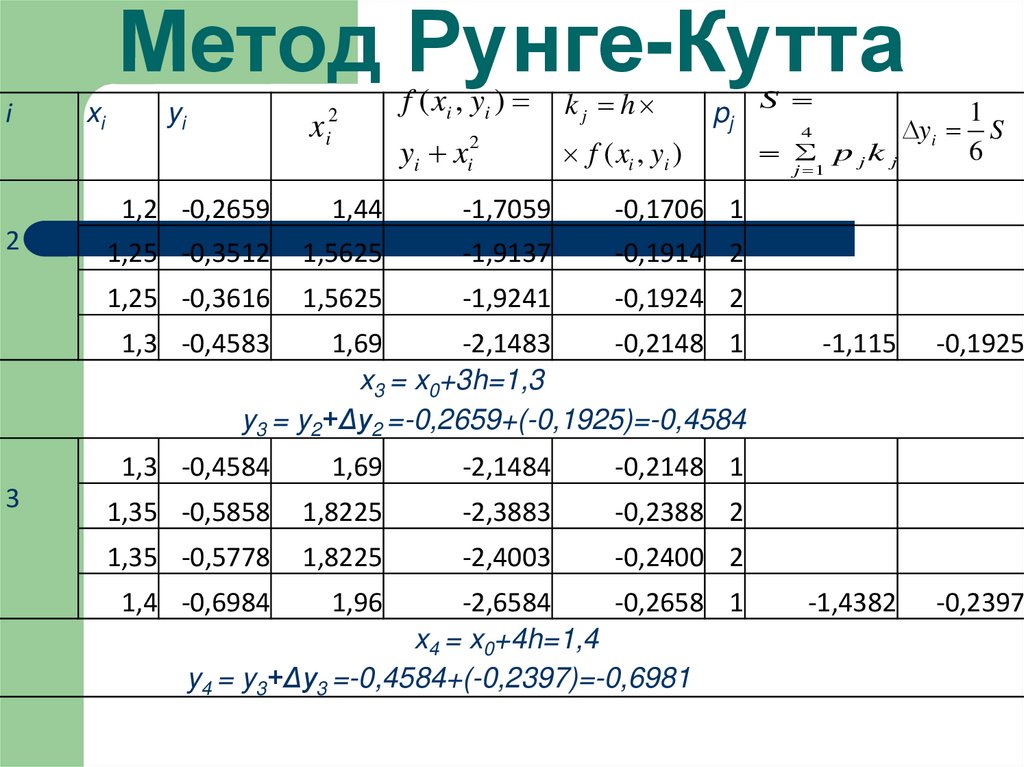
25. Метод Рунге-Кутта

i
2
xi
yi
x
2
i
f ( xi , yi )
yi xi2
k j h
f ( xi , yi )
pj
1,2 -0,2659
1,44
-1,7059
-0,1706 1
1,25 -0,3512
1,5625
-1,9137
-0,1914 2
1,25 -0,3616
1,5625
-1,9241
-0,1924 2
1,3 -0,4583
1,69
-2,1483
-0,2148 1
x3 = x0+3h=1,3
y3 = y2+Δy2 =-0,2659+(-0,1925)=-0,4584
3
1,3 -0,4584
1,69
-2,1484
-0,2148 1
1,35 -0,5858
1,8225
-2,3883
-0,2388 2
1,35 -0,5778
1,8225
-2,4003
-0,2400 2
1,4 -0,6984
1,96
-2,6584
-0,2658 1
x4 = x0+4h=1,4
y4 = y3+Δy3 =-0,4584+(-0,2397)=-0,6981
S
4
p jk j
j 1
yi
1
S
6
-1,115
-0,1925
-1,4382
-0,2397

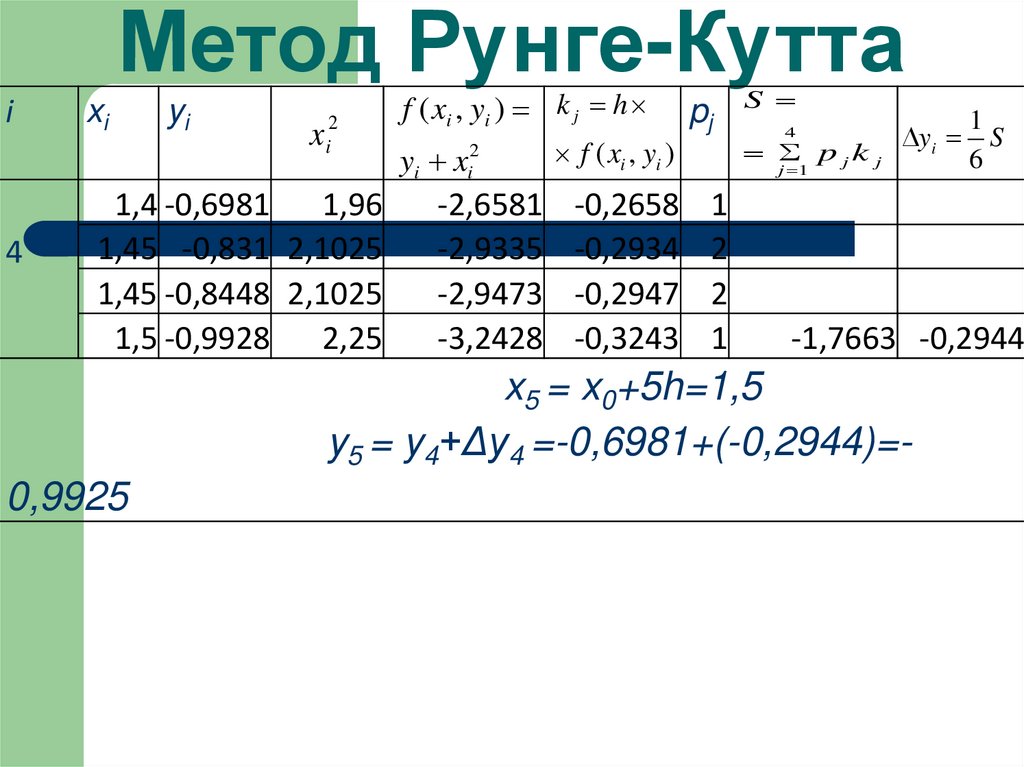
26. Метод Рунге-Кутта

i
4
xi
yi
x
2
i
1,4 -0,6981
1,96
1,45 -0,831 2,1025
1,45 -0,8448 2,1025
1,5 -0,9928
2,25
f ( xi , yi ) k j h
yi xi2
-2,6581
-2,9335
-2,9473
-3,2428
f ( xi , yi )
-0,2658
-0,2934
-0,2947
-0,3243
pj
S
4
p jk j
yi
j 1
1
2
2
1
-1,7663 -0,2944
x5 = x0+5h=1,5
y5 = y4+Δy4 =-0,6981+(-0,2944)=-
0,9925
1
S
6

27. Домашнее задание

Работа с конспектом
1. Решить задачу: Проинтегрировать
методом Эйлера дифференциальное
уравнение y`=2(x+y) с начальным условием
y(0)=0 на отрезке[1;2], приняв h=0,2.
Вычисления вести с четырьмя знаками
после запятой

28.

2. Методом Рунге-Кутта, приняв h=0,1, найти
приближённые решения дифференциальных
уравнений, удовлетворяющие условиям:
y x y
y (0) 1
x [0,1]