3_3 Опред инт24ф

1.

§ 6. Понятие определенного интеграла,
его геометрический и физический
смысл, основные свойства
Задачи, приводящие к понятию определенного интеграла
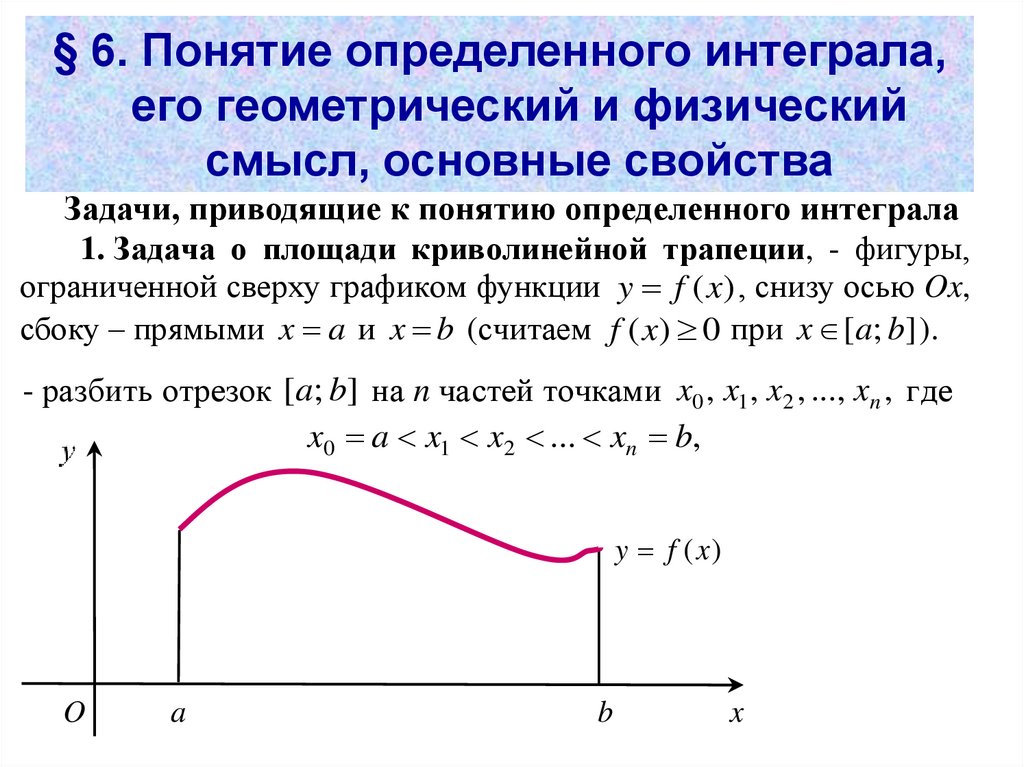
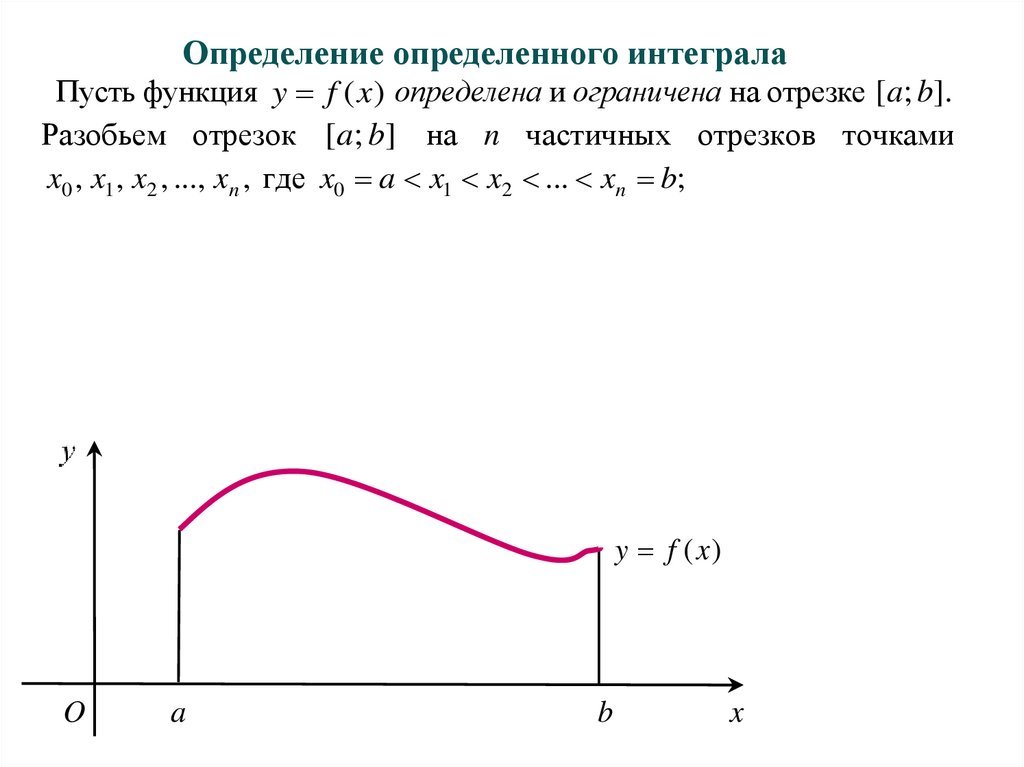
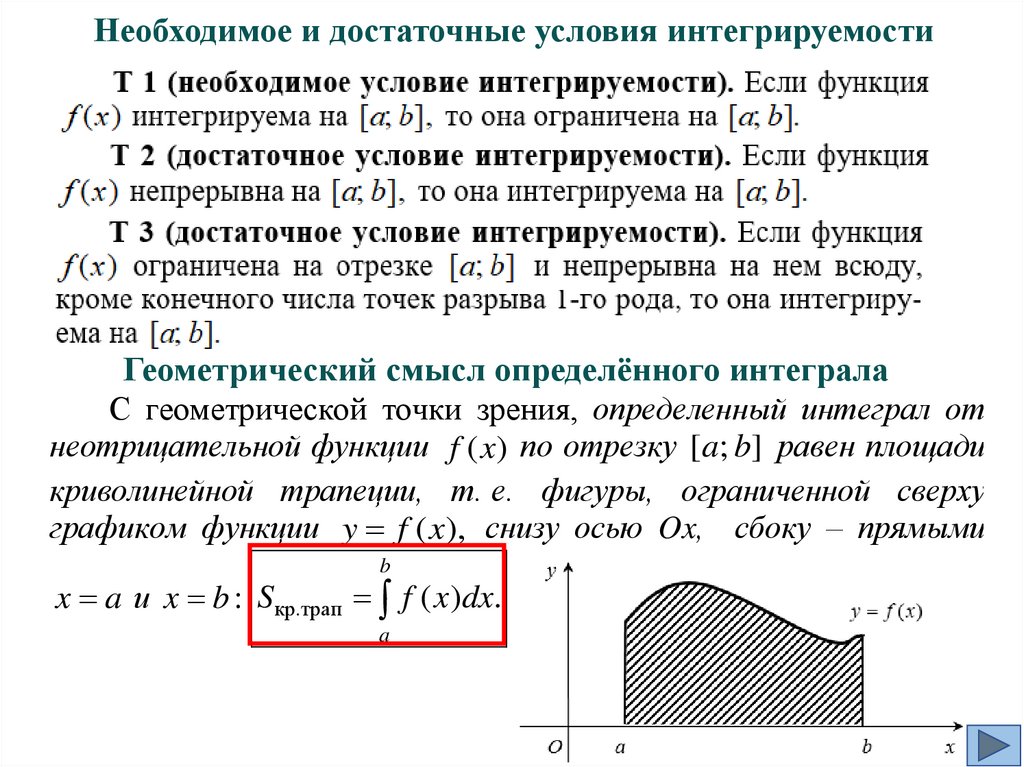
1. Задача о площади криволинейной трапеции, - фигуры,
ограниченной сверху графиком функции y f ( x) , снизу осью Ox,
сбоку – прямыми x a и x b (считаем f ( x) 0 при x [a; b] ).
- разбить отрезок [a; b] на n частей точками x0 , x1 , x2 , ..., xn , где
x0 a x1 x2 ... xn b,
y f ( x)
O
a
b
x

2.

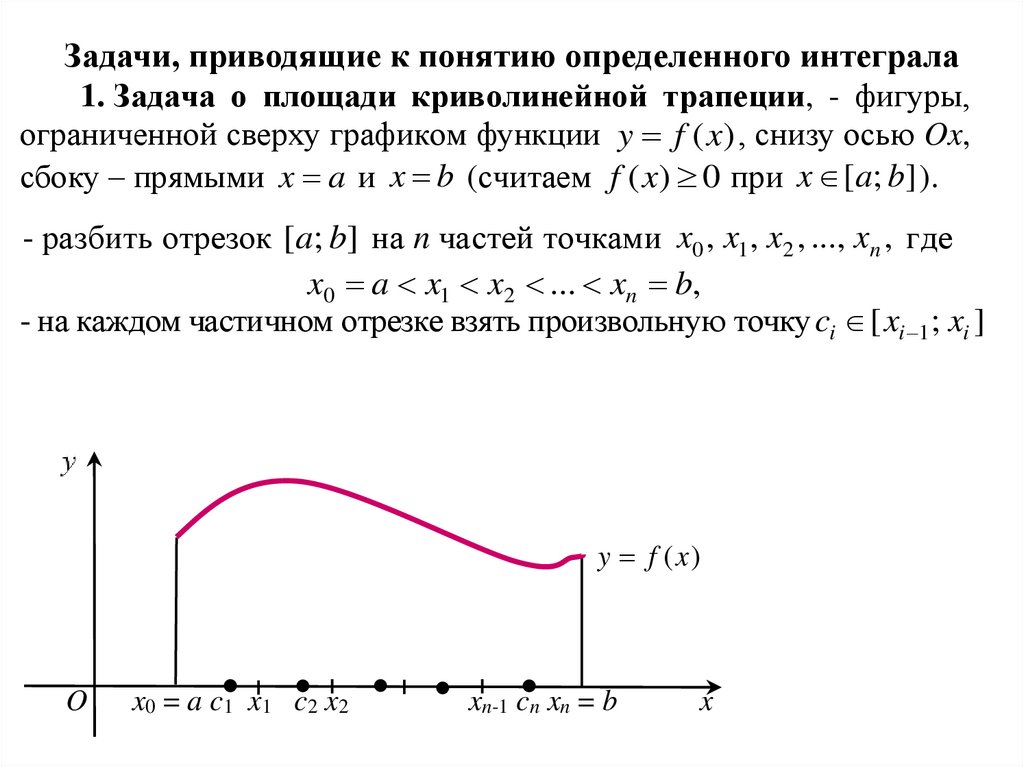
Задачи, приводящие к понятию определенного интеграла
1. Задача о площади криволинейной трапеции, - фигуры,
ограниченной сверху графиком функции y f ( x) , снизу осью Ox,
сбоку – прямыми x a и x b (считаем f ( x) 0 при x [a; b] ).
- разбить отрезок [a; b] на n частей точками x0 , x1 , x2 , ..., xn , где
x0 a x1 x2 ... xn b,
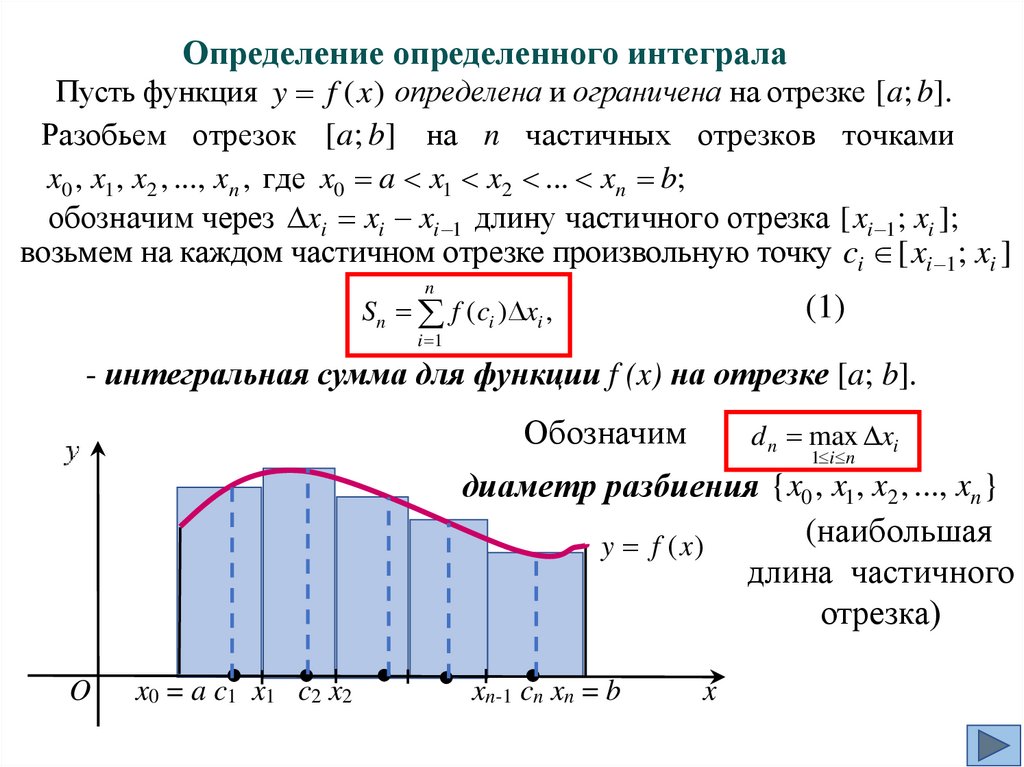
- на каждом частичном отрезке взять произвольную точку ci [ xi 1 ; xi ]
y f ( x)
O
x0 = a c1 x1 c2 x2
xn-1 cn xn = b
x

3.

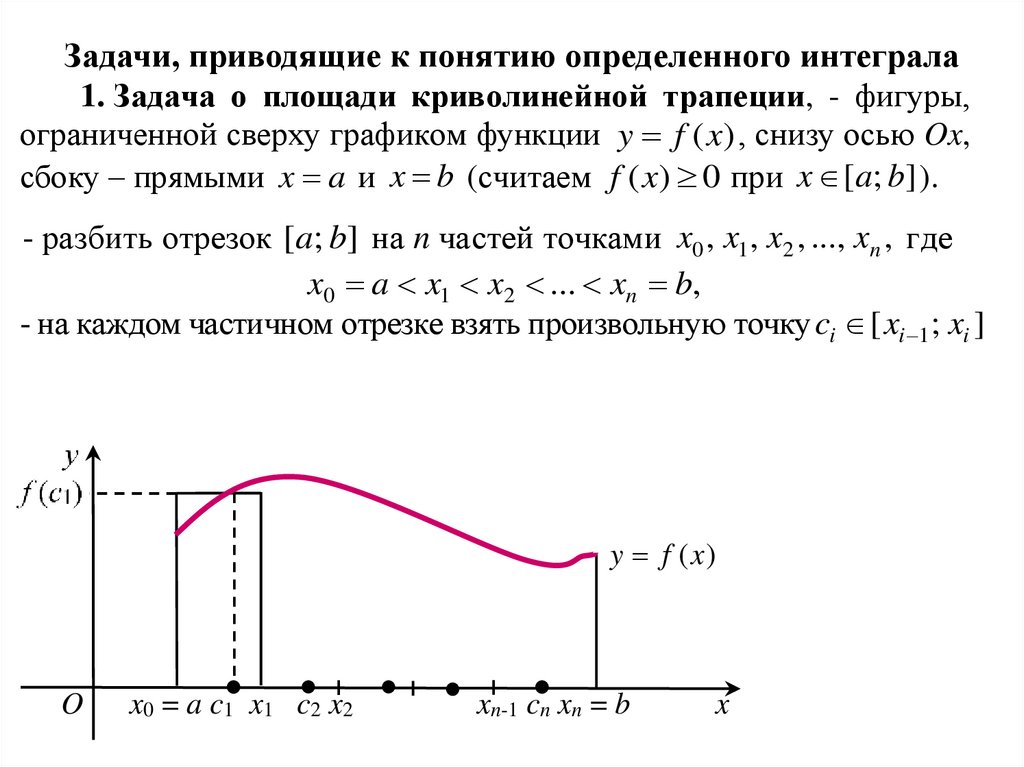
Задачи, приводящие к понятию определенного интеграла
1. Задача о площади криволинейной трапеции, - фигуры,
ограниченной сверху графиком функции y f ( x) , снизу осью Ox,
сбоку – прямыми x a и x b (считаем f ( x) 0 при x [a; b] ).
- разбить отрезок [a; b] на n частей точками x0 , x1 , x2 , ..., xn , где
x0 a x1 x2 ... xn b,
- на каждом частичном отрезке взять произвольную точку ci [ xi 1 ; xi ]
y f ( x)
O
x0 = a c1 x1 c2 x2
xn-1 cn xn = b
x

4.

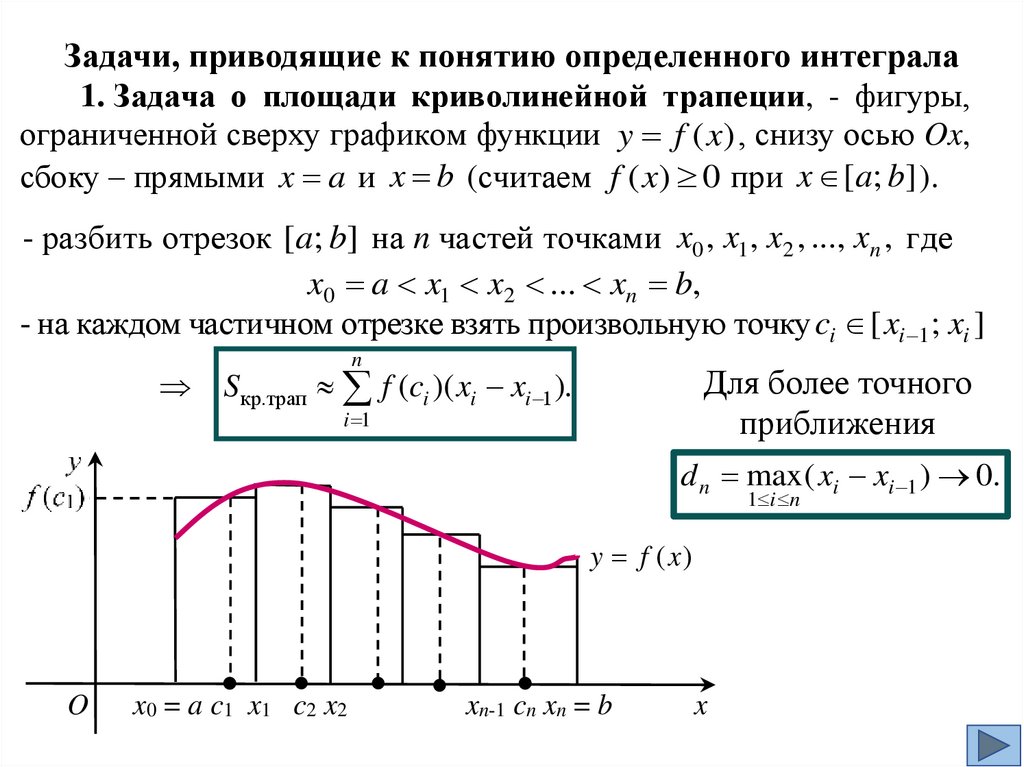
Задачи, приводящие к понятию определенного интеграла
1. Задача о площади криволинейной трапеции, - фигуры,
ограниченной сверху графиком функции y f ( x) , снизу осью Ox,
сбоку – прямыми x a и x b (считаем f ( x) 0 при x [a; b] ).
- разбить отрезок [a; b] на n частей точками x0 , x1 , x2 , ..., xn , где
x0 a x1 x2 ... xn b,
- на каждом частичном отрезке взять произвольную точку ci [ xi 1 ; xi ]
n
Sкр.трап f (ci )( xi xi 1 ).
Для более точного
приближения
i 1
d n max( xi xi 1 ) 0.
1 i n
y f ( x)
O
x0 = a c1 x1 c2 x2
xn-1 cn xn = b
x

5.

2. Задача о работе переменной по величине силы F ,
направленной вдоль оси Ox, при перемещении материальной точки
по оси Ox от x a до x b.
Известно, что если сила
постоянна по величине и
направлению, то
Пусть F ( x ) – величина силы в точке x.
A F s F s cos ,
Разобьем отрезок [a; b] на n частей
точками x0 , x1 , x2 , ..., xn , где
причем у нас cos 1,
т.к. F Ox, s Ox.
x0 a x1 x2 ... xn b,
так, чтобы на каждом частичном отрезке [ xi 1; xi ] величину силы
можно было считать постоянной и равной F ( ci ), где ci [ xi 1 ; xi ]
n
n
A Ai F (ci )( xi xi 1 ),
i 1
i 1
причем для более точного
приближения нужно, чтобы
длины
всех
частичных
отрезков стремились к 0, т. е.
d n max( xi xi 1 ) 0.
1 i n

6.

3. Задача о массе неоднородного стержня. Пусть на отрезке
[a; b] лежит стержень и известна функция ( x), выражающая
плотность материала стержня в каждой точке x [a; b].
Будем считать, что стержень цилиндрический с постоянной
площадью поперечного сечения, равной 1.
Известно: если плотность
Разобьем отрезок [a; b] на n частей
тела постоянна, то m = γV.
точками x0 , x1 , x2 , ..., xn , где
У нас объем цилиндричеx0 a x1 x2 ... xn b,
так, чтобы на каждом частичном
отрезке