Лекция 2 Прямые методы решения СЛАУ

1. Прямые методы решения систем линейных алгебраических уравнений

Метод Гаусса, теорема о LU- разложении,
условия применимости метода Гаусса,
метод Гаусса с выбором главного элемента,
условия применимости. Вычисление
определителя. Обращение матрицы. Метод
квадратного корня решения СЛАУ. Метод
прогонки решения СЛАУ с
трехдиагональной матрицей.
Безбородникова Р.М.

2. Введение

Большинство прикладных расчетных задач сводится
к решению СЛАУ (систем линейных алгебраических
уравнений).
Роль выбора эффективного способа решения СЛАУ
играет важную роль.
Нужно уметь ориентироваться среди методов,
программ, разбираться в алгоритмах, учитывающих
специфику постановок задач, знать их сильные и
слабые стороны, а также границы применимости.
2

3. Постановка задачи СЛАУ

• Требуется найти численное решение систем
вида a11 x1 a12 x2 ... a1n xn b1 ,
a x a x ... a x b ,
21 1
22 2
2n n
2
....................................................
a n1 x1 a n 2 x2 ... a nn xn bn ,
(1)
или в векторно-матричном виде: Ax b (1а)
где
T
b b1, b 2 , ... b n - вектор свободных членов
x x1, x 2 , ... x n T - вектор неизвестных
A a ij in, j 1 - вещественная матрица
det A 0
коэффициентов системы
3

4. Эффективность решения

Эффективность способов решения системы (1) во
многом зависит от структуры и свойств матрицы А
(размера, обусловленности, симметричности,
заполненности, специфики расположения нулевых
элементов и т.д.).
При небольших n для нахождения решения можно
применять формулу Камера:
det Ai
xi
, i 1, n
det A
С ростом n возрастает погрешность вычислений
при расчете определителя.
4

5. Метод Гаусса

• Суть метода Гаусса – последовательное
исключение неизвестных слагаемых системы.
• Осуществляется это посредством приведения
матрицы коэффициентов к верхнетреугольному
виду (прямой ход), и на основе полученной
матрицы находятся неизвестные в обратном
порядке, т.е. с последней до первой (обратный
ход).
• Метод Гаусса предполагает что все главные
миноры матрицы А отличны от нуля, иначе
система не имеет однозначного решения.
5

6. Прямой ход (1 шаг)

a 21
• Разделим первую строку (1) на
и вычтем
a11
из второго уравнения.
a 31
• Разделим первую строку (1) на
и вычтем
a11
из третьего уравнения и т.д. В результате на
1 –ом шаге получим:
a11x1 a12 x 2 ... a1n x n b1,
(1)
(1)
(1)
a 22 x 2 ... a 2 n x n b 2 ,
(1)
(1)
(1)
a
x
...
a
x
b
32 2
3n n
3 ,
....................................................
(1)
(1)
(1)
a
x
...
a
x
b
nn n
n
n2 2
где
(2)
(1)
a
a ij(1) a ij i1 a1 j
a11
(1)
a
bi(1) bi i1 b1
a11
i, j 2,.., n
6

7. Прямой ход (2 шаг)

a 32
• Разделим вторую строку (2) на
и вычтем
a 22
из третьего уравнения.
a 42
• Разделим вторую строку (2) на a и вычтем
22
из четвертого уравнения и т.д. В результате
на 2 –ом шаге получим:
... a1n x n b1,
a11x1 a12 x 2
(1)
(1)
(1) где
(2)
a
x
...
a
x
b
22 2
2n n
2 ,
(1)
a
( 2)
( 2)
( 2)
( 2)
(1)
i2 a
a
x
...
a
x
b
,
a
a
33 3
3n n
3
2j
ij
ij
(1)
a 22
...............................................................
(1)
a
( 2)
(1)
i 2 b (1)
b
b
( 2)
( 2)
( 2)
2
i
i
(1)
a
x
...
a
x
b
a
nn n
n
n3 3
22
7
i, j 3,.., n

8. Прямой ход (n-1 шаг)

• В результате на (n-1) –ом шаге получим:
... a1n x n b1,
a11x1 a12 x 2
(1)
(1)
(1)
a
x
...
a
x
b
22 2
2n n
2 ,
...............................................................
( n 1)
( n 1)
a nn x n b n
где
a ij( k ) a ij( k 1)
(3)
( k 1)
a ik
( k 1)
a
,
kj
( k 1)
a kk
( k 1)
a
( k 1)
bi( k ) bi( k 1) ik
b
,
k
( k 1)
a kk
(4)
k 1,.., n 1
i, j k 1,.., n
8

9. Обратный ход

• Находим неизвестные в обратном порядке:
• Или обобщенно:
(5)
9

10. Алгоритм решения СЛАУ методом Гаусса

10

11. Модификации метода

• Рассмотренный метод называется методом Гаусса единственного
решения.
• Так как реальные машинные вычисления производятся не с
точными, а с усеченными числами, то выполнение алгоритма
может прекратиться, если на каком то этапе знаменатели дробей
окажутся равным нулю или очень маленькими числами. Чтобы
уменьшить влияние ошибок округлений и исключить деление на
ноль, на каждом этапе прямого хода столбцы матрицы
коэффициентов уравнений системы обычно переставляют так,
чтобы деление производилось на наибольший по модулю в
данном столбце (обрабатываемом подстолбце) элемент.
• Числа, на которые производятся деление в методе Гаусса,
называются ведущими, или главными элементами. Отсюда
название рассматриваемой модификации метода, исключающее
деление на ноль и уменьшающее вычислительные погрешности, метод Гаусса с постолбцовым выбором главного элемента.
11

12. Модификации метода

• Для реализации метода Гаусса с постолбцовым
выбором главного элемента между строками 1 и
2 алгоритма необходимо добавить условие
(проверка на разрешимость):
• Если деление выполняется на элемент,
наибольший по модулю во всей матрице,
преобразуемой на рассматриваемом этапе, то
метод Гаусса называют методом главных
элементов.
12

13. Применение метода Гаусса к вычислению определителей матриц

• Преобразования прямого хода метода Гаусса не
изменяют определителя матрицы А, поэтому метод
можно использовать для нахождения определителя
матрицы А.
• Определитель треугольной матрицы равен
произведению диагональных (ведущих) элементов:
13

14. Применение метода Гаусса к вычислению определителей матриц

• Для вычисления определителя алгоритм метода Гаусса
единственного деления должен быть дополнен последней
строкой:
• А при постолбцовом выборе главного элемента:
14

15. Применение метода Гаусса к обращению матриц

• Для получения обратной матрицы А-1 будем исходить из
того, что она является решением уравнения
АХ=Е.
(6)
Подставляя искомую матрицу Х как набор векторстолбцов, а единичную матрицу Е как набор единичных
векторов матричное уравнение (6) можно заменить
системой векторно-матричных уравнений:
(7)
Аx1=e1, Аx2=e2, …, Аxn=en.
• Каждое уравнение может быть решено методом Гаусса. При
этом все СЛАУ имеют одну и ту же матрицу коэффициентов.
Поэтому достаточно один раз привести матрицу А к
треугольному виду.
• В алгоритме метода Гаусса надо «размножить» строки 4 и 9
так, чтобы в роли вектора b оказались все единичные
векторы. В результате будем получать столбцы обратной
матрицы.
15

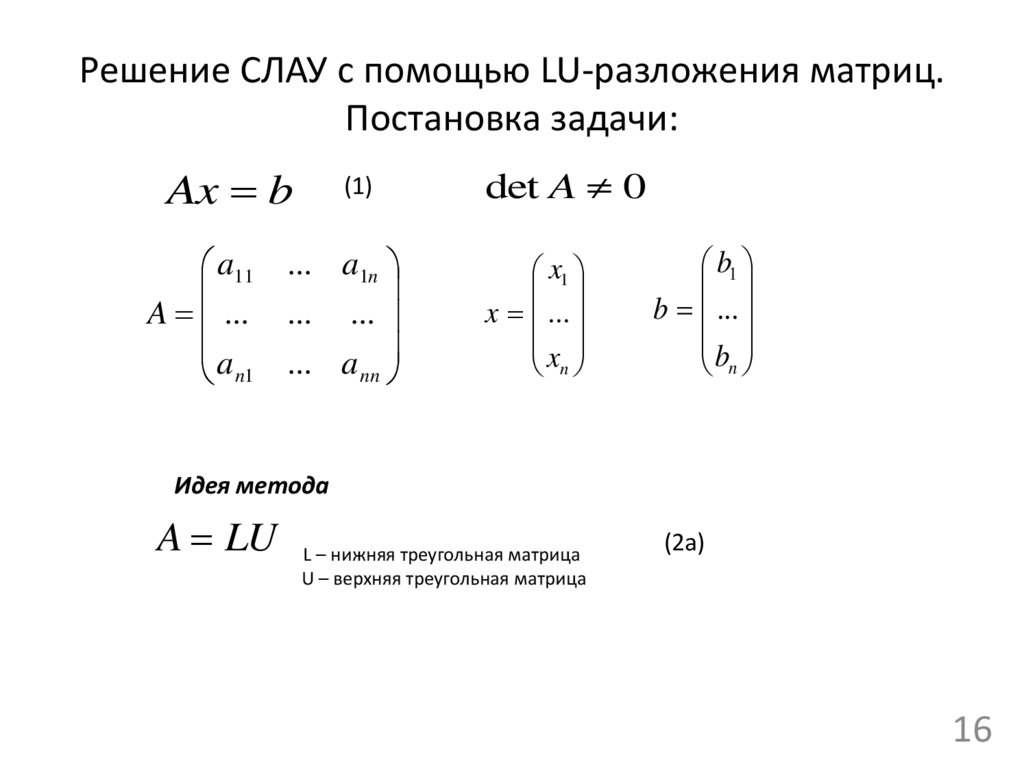
16. Решение СЛАУ с помощью LU-разложения матриц. Постановка задачи:

Ax b
(1)
a11 ... a1n
A ... ... ...
a
...
a
nn
n1
det A 0
x1
x ...
x
n
b1
b ...
b
n
Идея метода
A LU L – нижняя треугольная матрица
(2а)
U – верхняя треугольная матрица
16

17. Теорема(об LU-разложении матрицы)

Если все главные угловые миноры матрицы А не равны нулю, то
матрицу А можно представить в виде
A LU
где L – нижняя треугольная матрица, U – верхняя треугольная матрица.
Если какая – либо из матриц L, U имеет ненулевую диагональ, то такое
разложение единственно.
17

18. Два вида разложения:

1)
1 0
l21 1
L
... ...
l
n1 ln 2
...
...
...
...
0
0
...
1
u11 u12
0 u22
U
... ...
0
0
... u1n
... u2 n
... ...
... unn
(3)
2)
l11 0
l
l
L 21 22
... ...
l
n1 ln 2
... 0
... 0
... ...
... lnn
1 u12
0 1
U
... ...
0 0
... u1n
... u2 n
... ...
... 1
(4)
18

19. Получение матриц L и U

1 0
l21 1
... ...
l
n1 ln 2
...
...
...
...
u11
u11l21
...
u l
11 n1
0 u11 u12
0 0 u22
*
... ...
...
1 0 0
...
...
...
...
u12
u12l21 u22
...
u1n
a11
u2 n
a21
...
...
a
unn
n1
a12
a22
...
an 2
... a1n
... a2 n
... ...
... ann
...
u1n
... u1nl21 u2 n
...
...
19

20. Получение расчетных формул для матриц L и U

u1 j a1 j ( j 1, n )
a i1
li1
(i 2, n )
u11
u 2 j a 2 j l 21u1 j ( j 2, n )
a i 2 li1u12
li 2
(i 3, n )
u 22
n 1
u nn a nn lnk u kn
k 1
20

21.

Получение расчетных формул
для матриц L и U
(продолжение)
i 1
u ij a ij lik u kj (i j)
k 1
j 1
1
(i j)
lij
a
l
u
ij
ik
kj
u jj
k 1
21

22. Первый шаг второго этапа

РЕШЕНИЕ СЛАУ С ПОМОЩЬЮ LU-РАЗЛОЖЕНИЯ
LUx b
y Ux
Ly b
Первый шаг второго этапа
y1 b1
l y y b
21 1
2
2
l31 y1 l32 y2 y3 b3
...
ln1 y1 ... yn bn
из системы находим y1 , y2 ,..., yn
i 1
или yi bi lik y k
k 1
22

23. Второй шаг второго этапа

Ux y
... u1n x n y1
u11x1 u12 x 2
u
x
...
u
x
y
22
2
2
n
n
2
u 33x 3 ... u 3n x n y3
...
u nn x n y n
из системы находим x n , x n 1 ,..., x1
n
1
или x i yi u ik x k
u ii
k i 1
23

24. Вычисление определителя матрицы в методе LU - разложения

Вычисление определителя матрицы в методе LU разложения
Метод Гаусса
Прямой ход
a11
0
A( n 1) 0
...
0
a12
a13
...
(1)
a22
0
(1)
a23
( 2)
a33
...
...
...
0
...
0
...
...
a1n
(1)
a2 n
a3( 2n)
...
( n 1)
ann
(1)
( 2)
( n 1)
det A det A( n 1) a11 a22
a33
... ann
LU-алгоритм
или
det A det(L U) det L det U
u11 u 22 ... u nn - I вид LU-разложения
l11 l22 ... lnn
- II вид LU-разложения
24

25. Обращение матрицы в методе LU - разложения

A L U A 1 U 1 L 1
Умножаем на U слева и на L справа. Получим:
U A 1 L 1
и
A 1L U 1
A A 1 E
Обозначим
x11 ... x1n
A 1 X ... ... ...
x ... x
nn
n1
25

26. Обращение матрицы в методе LU - разложения

26

27. Разложение симметричных матриц. Метод квадратных корней

Пусть А – симметричная матрица, т.е. aij=aji. Построим ее
разложение в виде A=UTU, где
Перемножим матрицы:
27

28. Метод квадратных корней

Общий вид формул:
i 1
u ii a ii u 2ki , i 1,...,n.
k 1
i 1
1
u ij
a ij u ki u kj
u ii
k 1
j=2, …,n(j>i).
28

29. Метод квадратных корней

• Таким образом, решение СЛАУ вида Ах=b
или UТUx=b сводится к системе вида:
29

30. Метод квадратных корней

30

31. Метод прогонки

Пусть матрица А имеет трехдиагональную структуру:
31

32. Метод прогонки

32

33. Метод прогонки

33

34. Метод прогонки: вычисление определителя

34

35. Условие применимости метода

Достаточным условием применимости метода прогонки
является требование диагонального преобладания в матрице А:
bi ci ai
(14)
Замечание
Диагональное преобладание гарантирует что угловые миноры
матрицы А отличны от 0
c1
1
b1
1 1
(15)
35