Похожие презентации:
Криволинейные интегралы
1.
2.
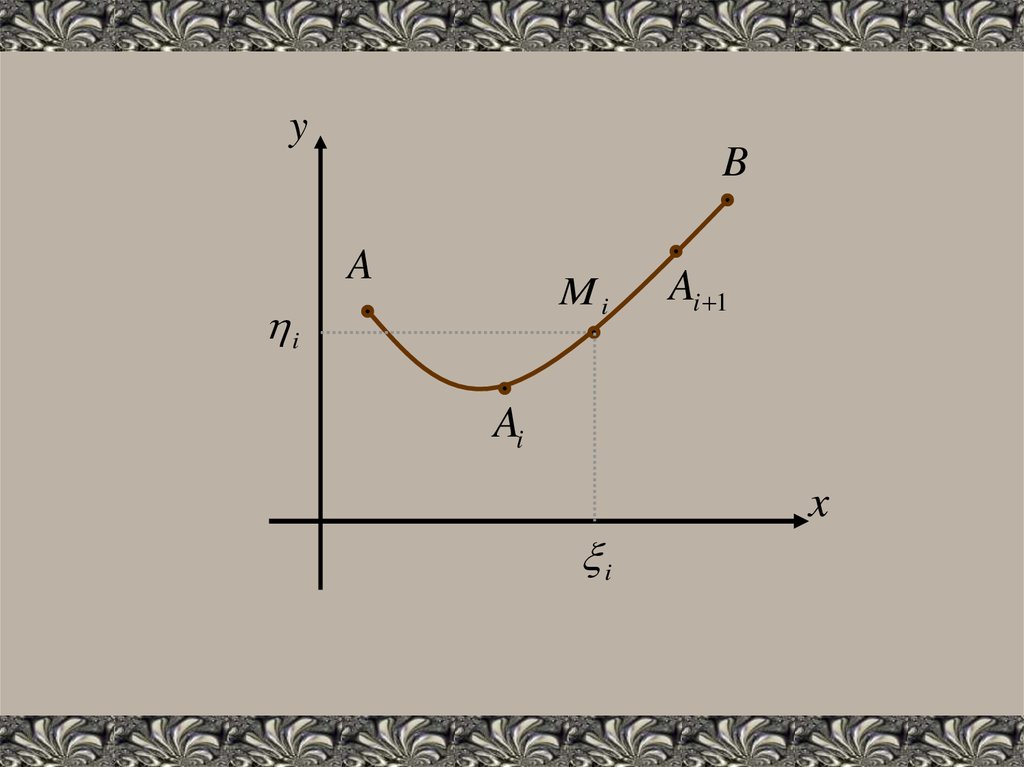
Рассмотрим произвольную функцию f(x,y),заданную вдоль непрерывной плоской
кривой АВ.
Разобьем эту кривую на элементарные
дуги AiAi+1. На каждой дуге выберем
точку
Mi(ξi,ηi)и
вычислим
значение
функции в этой точке:
f ( i , i ) f (M i )
3.
yB
A
Mi
i
Ai 1
Ai
x
i
4.
Сумму видаn
f ( , )
i 1
i
i
i
где σi – длина элементарной
дуги, называют интегральной
суммой для функции f(x,y)
по кривой АВ.
5.
Если существует конечный пределинтегральной суммы при стремлении
к нулю наибольшей из всех длин
дуг, не зависящий от способа
разбиения кривой АВ и выбора
точек
Mi,
то
он
называется
криволинейным интегралом первого
рода от функции f(x,у) по кривой
АВ.
n
lim
max i 0
f ( , )
i 1
i
i
i
f ( x, y)dS
AB
6.
Где S – длина дуги кривой.Направление кривой роли не играет:
f ( x, y)dS f ( x, y)dS
AB
BA
Аналогично строятся рассуждения
пространственных кривых:
f ( x, y, z)dS f ( x, y, z)dS
AB
BA
для





 Математика
Математика








