Рассеяние света малыми частицами

1. Рассеяние света малыми частицами

Будак Владимир Павлович,
Национальный исследовательский
университет «МЭИ»
кафедра светотехники
: +7 (495) 763-5239
BudakVP@mpei.ru

2. Основные понятия рассеяния на частице

Z
Имеем для облученностей при рассеянии на частице плоской волны
( , )
(ˆl )
ˆ
E (l ) E ( , )
E0 2 E0
E
2
r
r
( , ) – коэффициент направленного рассеяния
Y
O
X
E0
ˆl )dˆl – коэффициент полного рассеяния
(
(ˆl , ˆl )
ˆ
ˆ
– индикатриса рассеяния света на частице
x(l , l )
– коэффициент ослабления света
Qa
– факторы поглощения,
, Qs , Qe
G
G
G
рассеяния, ослабления
Все коэффициенты имеют размерность L-2,
а факторы безразмерны

3. Рассеянное поле

Пусть падает скалярная плоская монохроматическая волна: u0 exp ikz i t
Рассеянная волна на большом расстоянии от частицы - сферическая:
exp ik r z
exp ikr i t
exp ikr ikz ikz i t
ˆ
ˆ
ˆ
u S (l )
S (l )
S (l )
u0
ikr
ikr
ikr
2
2
ˆ
ˆ
ˆ
S ( l ) – амплитудная функция рассеяния E ~ u (l ) S (l )
S (ˆl )
u
u
u
1
exp
ik
r
z
На большом расстоянии от частицы
0
0
ikr
2
2
1 1
Приближение Fresnel: z : r z 2 2 z
, r z
,
2z
2z r z
2
2
ˆ
S (ˆl )
S (l )
2 Const
2
u0 u 1
exp ik 1 2 Re
exp ik
2
ikz
2z
ikz
2
z
z
При рассеянии интересует поле на больших расстояниях от
рассеивающей частицы

4. Оптическая теорема

Коэффициент ослабления:
u0 u u0
2
u0
2
2
dxdy
S (0)
S (0) 2
2
2
2 Re
exp ik dxdy 2 Re
exp ik d d
2z
2z
ikz
ikz 0 0
2
S (0)
4
4 Re
exp
ik
d
2 Re S (0)
2
2z
k
ik d
ikz 0
ik , d
2z
z
Соответственно, зная амплитудный коэффициент рассеяния
можно определить все характеристики рассеяния

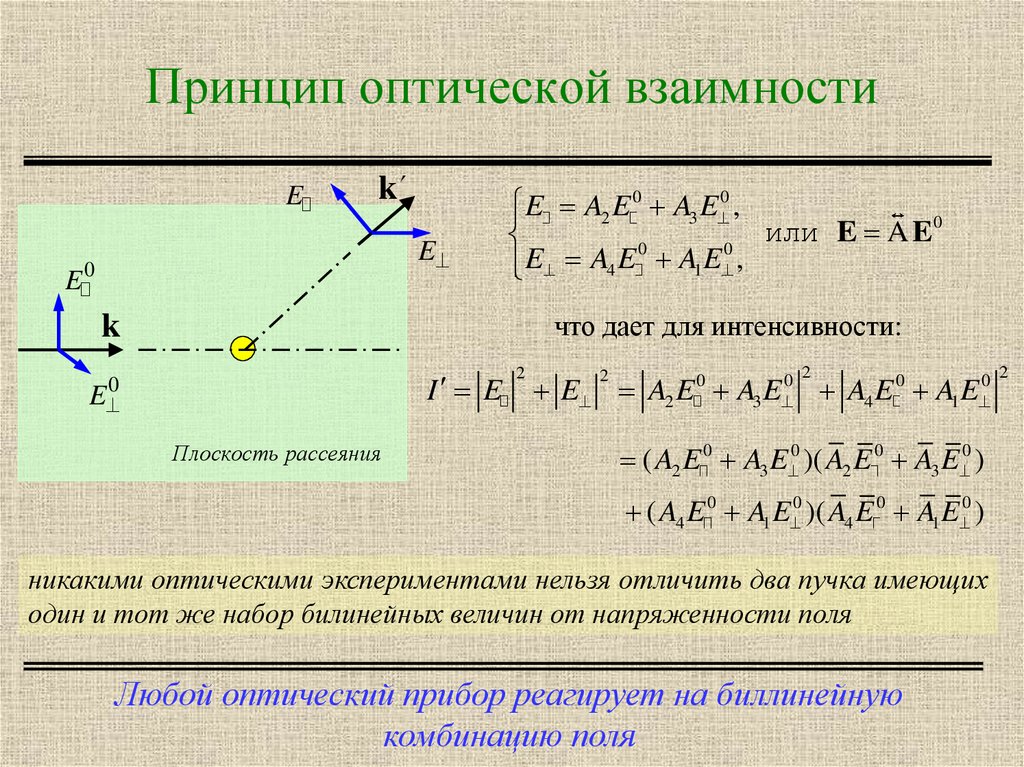
5. Принцип оптической взаимности

E
E
k´
E
0
0
0
E
A
E
A
E
2
3 ,
0
или
E
A
E
0
0
E
A
E
A
E
4
1 ,
что дает для интенсивности:
k
I E
E 0
Плоскость рассеяния
2
0 2
E A2 E A3 E
2
0
0 2
A4 E A1E
0
( A2 E 0 A3 E 0 )( A2 E 0 A3 E 0 )
( A4 E 0 A1 E 0 )( A4 E 0 A1E 0 )
никакими оптическими экспериментами нельзя отличить два пучка имеющих
один и тот же набор билинейных величин от напряженности поля
Любой оптический прибор реагирует на биллинейную
комбинацию поля

6. Параметры Стокса (Stokes)

S0 E E * E E * ,
S1 E E * E E * ,
S2 E E * E E * 2 Re E E * , S3 i E E * E E * 2 Im E E *
S0 L – яркость излучения;
S12 S22
Lmax Lmin
– степень линейной поляризации;
p
Lmax Lmin
S0
S3
q
– степень круговой поляризации: q>0 – правое вращение, q>0 – левое
S0
вращение, q=±1 – циркулярная, q=0 – линейная поляризация
r
S12 S22 S32
– степень однородности луча;
S0
Следовательно, можно определить различную комбинацию
параметров, но всегда их будет 4, поскольку существуют
4 различных типа приемников: естественный, линейные
вертикально и горизонтально, циркулярной поляризации

7. Вектор-параметр Стокса

Поляризация частично-когерентного света: фаза и амплитуда изменяются
хаотически, сохраняя в среднем разность фаз и отношение амплитуд двух
компонент
Все параметры Стокса имеют размерность яркости и соответствуют
измерению яркомером с поляризационным фильтром: нейтральный, два
скрещенных линейных (0º и 45º) и циркулярным
Параметры Стокса определяются для луча относительно некоторой
плоскости – плоскость референции
0
0
1
S S1 , S2 , S3 , S4 , S Si
0 cos 2 sin 2
i
S R S, R
E E*
E E *
0 sin 2 cos 2
*
E E *
0
0
E E
0
0
0
0
1
Реакция любого оптического приемника выражается через
вектор-параметр Стокса

8. Преобразование параметров Стокса

Преобразование вектор-параметра Стокса выражается через матрицу 4 4
Мюллера (Mueller) – линейность среды: S(r, ˆl ) D(ˆl, ˆl )S(r, ˆl )
В частности при рассеянии – матрица рассеяния:
Incident ray
Z
ˆl
Scattered ray
c
ˆl
c
Y
O
f
X
f
Reference plane
Reference plane of scattered ray
of incident ray
d11 (ˆl , ˆl )
ˆl , ˆl )
d
(
21
D(ˆl , ˆl )
ˆ ˆ
d31 (l , l )
d (ˆl , ˆl )
31
d12 (ˆl , ˆl ) d13 (ˆl , ˆl ) d14 (ˆl , ˆl )
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
d 22 (l , l ) d 23 (l , l ) d 24 (l , l )
d32 (ˆl , ˆl ) d33 (ˆl , ˆl ) d34 (ˆl , ˆl )
d32 (ˆl , ˆl ) d33 (ˆl , ˆl ) d34 (ˆl , ˆl )
ˆl , ˆl )dˆl , x (ˆl , ˆl ) 4 D(ˆl , ˆl )
d
(
11
(ˆl, )S(r, ˆl ) Q(r, ˆl )S(r, ˆl ) R(c ) D(r; ˆl , ˆl ) R(c)S(r, ˆl )dˆl
Q(r, ˆl )
ij
ij , ,
В общем случае мутная (рассеяние + поглощение) среда
является двулучепреломляющей и дихроичной

9. Теория Ми (Gustav Mie, Greifswald, 1908)

– строгое решение уравнений Maxwell при рассеянии плоской волны на
металлическом шаре
2
2
2 2
n n i n, n i
, ( n k )E(r ) 0
Сущность решения Mie – представление поля через вектора Herz:
e r e ru, m r m rv
где скалярная волна удовлетворяет скалярному волновому уравнению:
( n2k 2 ) (r) 0, E Mv iNu , H n Mu iNv , M rot(r ), nkN rot M
M – магнитные колебания: Er=0, Hr≠0; N – электрические: Er ≠ 0, Hr=0;
Решение скалярного волнового уравнения известно: lm (r , , ) Ylm ( , ) Zl ( nkr )
1 ( m |m|)
d m Pl (cos )
2l 1 (l | m |)!
|m|
im
m
2
Y ( , )
( 1)
Pl (cos ) e , Pl (cos )
4 (l | m |)!
d m
2l 1
l
P0 (cos ) 1, Pl 1 (cos )
Pl (cos ) cos
Pl 1 (cos ); Zl ( )
z l 1 ( )
l 1
l 1
2 2
m
l
По сути решение Ми есть единственное нетривиальное решение
уравнений Максвелла!

10. Поле рассеянной волны

Компоненты Er и Hr убывают быстрее 1/r и при r → ∞ обращаются в 0:
E H
i ikr
i
e S 2 ( ) cos , E H e ikr S1 ( ) cos
kr
kr
где амплитудные функции рассеяния
2m 1
2m 1
S1 ( )
a
(cos
)
b
(cos
)
,
S
(
)
m m
2
bm m (cos ) am m (cos )
m m
n 1 m( m 1)
n 1 m( m 1)
d Pm (cos( )
d
m (cos )
, m (cos )
m (cos )
d cos
d
Коэффициенты am и bm определяются из граничных условий на шаре радиуса a:
am
m ( y ) m ( x) n m ( y ) m ( x)
n m ( y) m ( x) m ( y) m ( x)
, bm
m ( y ) m ( x) n m ( y ) m ( x)
n m ( y) m ( x) m ( y) m ( x)
m ( z)
z
z
2 a
J m 1 2 ( z ), m ( z )
H m 1 2 ( z), x ka
, y nx
2
2
Расчеты по формулам теории Ми до недавнего времени
представляли трудоемкую и сложную задачу

11. Явление рассеяния

E 0 E0 cos , E 0 E0 sin , E E , E E
Следовательно, S1(θ) и S2(θ) – амплитудные функции рассеяния, через которые
выражается матрица рассеяния, в частности
( , )
i1 ( ) i2 ( )
4 S (0) S 2 (0)
2
2
, i1 ( ) S1 ( ) , i2 ( ) S 2 ( ) , 2 Re 1
2
k
2
Для качественного анализа явления рассеяния можно представить, что
рассеянная волна состоит из компонент:
1. отраженная
1
2. преломленная
2 3. дифракция
4. краевой эффект: распределение вперед
3
5. поверхностная волна: “рябь” на Qe(λ), точное
рассеяние назад, глории
Принцип локализации Debye: am и bm имеют сложный характер
при x << m, убывают при m~x и равны 0 при x>m