Похожие презентации:
Понятие логарифма
1. Понятие ЛОГАРИФМа
ПОНЯТИЕЛОГАРИФМА
2. Для чего были придуманы логарифмы ?
ДЛЯ ЧЕГО БЫЛИ ПРИДУМАНЫЛОГАРИФМЫ ?
КАК СКАЗАЛ ФРАНЦУЗСКИЙ МАТЕМАТИК П. ЛАПЛАС,
«ИЗОБРЕТЕНИЕ ЛОГАРИФМОВ,
СОКРАТИВ РАБОТУ
АСТРОНОМОВ, ПРОДЛИЛО ИМ
ЖИЗНЬ».
3. Для чего были придуманы логарифмы ?
ДЛЯ ЧЕГО БЫЛИ ПРИДУМАНЫЛОГАРИФМЫ ?
…Если необходимость совершать
обратную операцию к операции
возведения в n-ую степень, была
осознана достаточно давно, то задача
нахождения показателя степени по
а в
заданному результату, т. е. задача
решения
х
уравнения а в стала
интересной лишь в XVII веке.
х
4.
Джон Непер(1550-1617)
– английский математик.
Изобретатель логарифмов,
составитель первой таблицы
логарифмов, облегчавшей
работу вычислителей многих
поколений и оказавшей
большое влияние на
развитие приложений
математики.
5.
Решите уравнения:2 8
2 3
x
2 2
x
x=3
x
3
2 2
x
x= ?
?
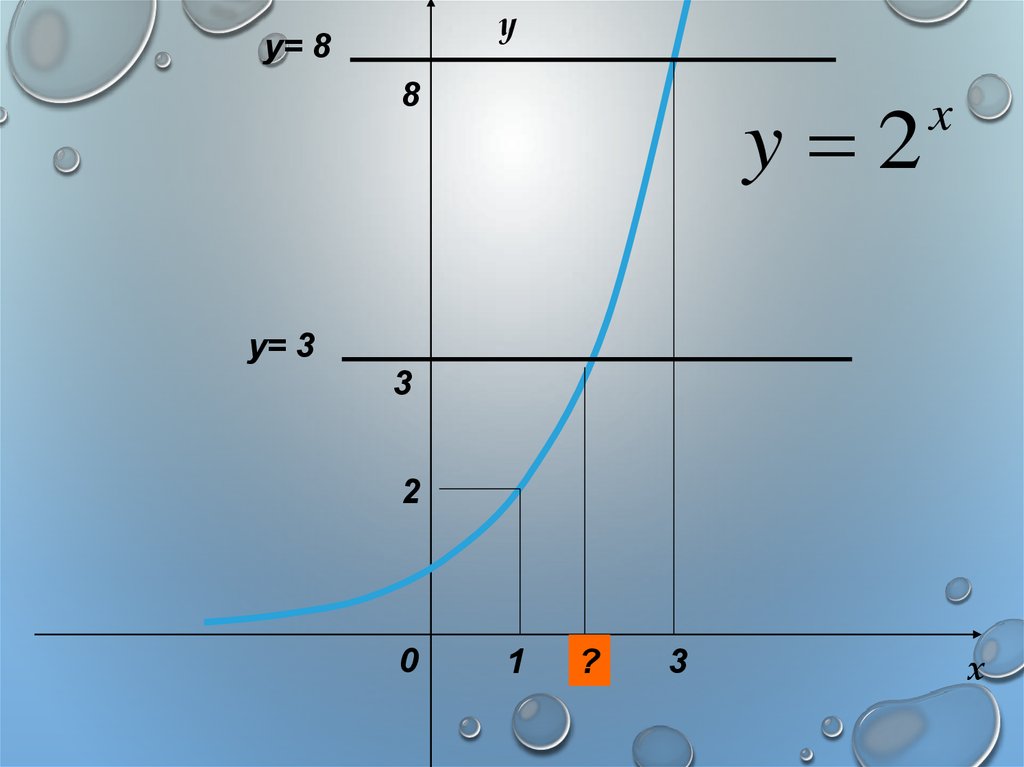
6.
yy= 8
8
y 2
x
y= 3
3
2
1
?
3
x
0
7.
Решите уравнения:2 8
x
2 2
x
x=3
3
2 3
x
2 2
x
?
x log 2 3
8. Возведение в степень имеет два обратных действия
ВОЗВЕДЕНИЕ В СТЕПЕНЬИМЕЕТ ДВА ОБРАТНЫХ
ДЕЙСТВИЯ
а
х
в
1. ОТЫСКАНИЕ A – ИЗВЛЕЧЕНИЕ КОРНЯ;
2. НАХОЖДЕНИЕ В – ЛОГАРИФМИРОВАНИЕ.
9. Определение
ОПРЕДЕЛЕНИЕ• ЛОГАРИФМОМ ПОЛОЖИТЕЛЬНОГО
ЧИСЛА В ПО ОСНОВАНИЮ А, ГДЕ
А>0,A=1,НАЗЫВАЕТСЯ ПОКАЗАТЕЛЬ
СТЕПЕНИ, В КОТОРУЮ НУЖНО
ВОЗВЕСТИ ЧИСЛО А ,ЧТОБЫ
ПОЛУЧИЛОСЬ В.
10.
• ВСПОМНИТЕ УРАВНЕНИЕ ИЗ ПЕРВОГОСЛАЙДА:
а в
х
МЫ ГОВОРИЛИ, ЧТО НАХОЖДЕНИЕ B –
ЛОГАРИФМИРОВАНИЕ. МАТЕМАТИКИ
ДОГОВОРИЛИСЬ ЗАПИСЫВАТЬ ЭТО ТАК:
log а в х
11. Например:
НАПРИМЕР:log 5 25 2,
1
log 4
2,
16
1
log 81 9 ,
2
log 1 27 3,
3
так как
так как
так как
так как
5 25
2
4
1
16
2
1
2
81 9
1
3
3
27
12. Найти значение логарифмов:
НАЙТИ ЗНАЧЕНИЕЛОГАРИФМОВ:
log 3 9
log 2 8
13. Найти значение логарифмов:
НАЙТИ ЗНАЧЕНИЕ ЛОГАРИФМОВ:log 4 4
log 7 7
log 5 5
log a a 1
14. Найти значение логарифмов:
НАЙТИ ЗНАЧЕНИЕ ЛОГАРИФМОВ:log 5 1
log 3 1
log a 1 0
log 4 ( 1)
Не имеет
смысла
15.
Определение логарифма можно записать так:a log a b = b
Это равенство справедливо при b>0, а>0, а≠1. Его
обычно называют основным логарифмическим
тождеством.
Например:
2
log 2 6
= 6;
3
– 2 log3 5
= (3
)
log 3 5
–2
=5
Вычислите:
3
log
10
8
3
log
log
2
18;
10
5;
2;
3
5log
3
2;
(1/4)
log
6;
(1/4)
9
12.
log
3
–2
= 1/25.
16.
Вычислить:Log 2 16;
log 2 64;
log
Log 2 1 ;
log 2 (1/2);
log 2 (1/8);
Log 3 27;
log 3 81;
log 3 3;
Log 3 1;
log 3 (1/9);
log 3 (1/3);
Log1/2 1/32;
Log0/5 (1/2);
log1/2 4;
log0,5 1;
2
2;
log0,5 0,125;
log1/2 2.
Дальше
17.
Сравните со своими ответами !Log 2 16;
log 2 64;
log 2 2;
Log 2 1 ;
log 2 (1/2);
log 2 (1/8);
Log 3 27;
log 3 81;
log 3 3;
Log 3 1;
log 3 (1/9);
log 3 (1/3);
Log1/2 1/32;
Log0,5 (1/2);
log1/2 4;
log0,5 1;
log0,5 0,125;
log1/2 2.
Таблица ответов:
4
0
3
0
5
1
6
-1
4
-2
-2
0
1
-3
1
-1
3
-1
18.
Домашнее задание.§14,
№№ 14.8, 14.13,
14.17, 14.23, 14.25








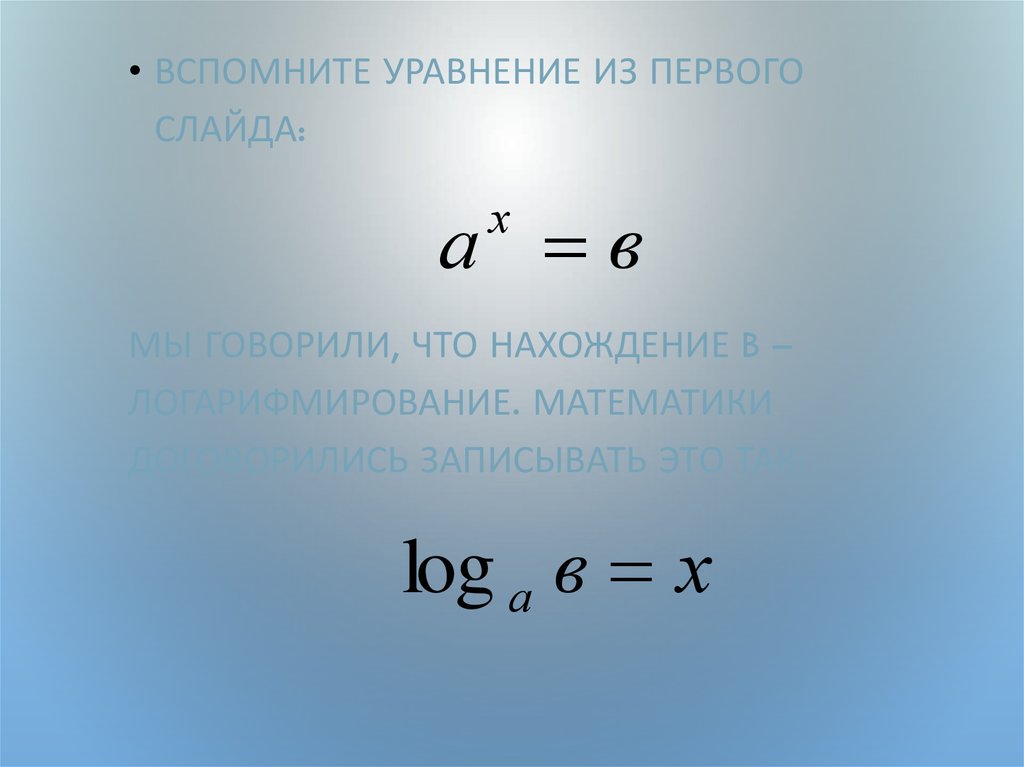








 Математика
Математика