Похожие презентации:
Синус, косинус, тангенс острого угла прямоугольного треугольника
1. Синус, косинус и тангенс острого угла прямоугольного треугольника
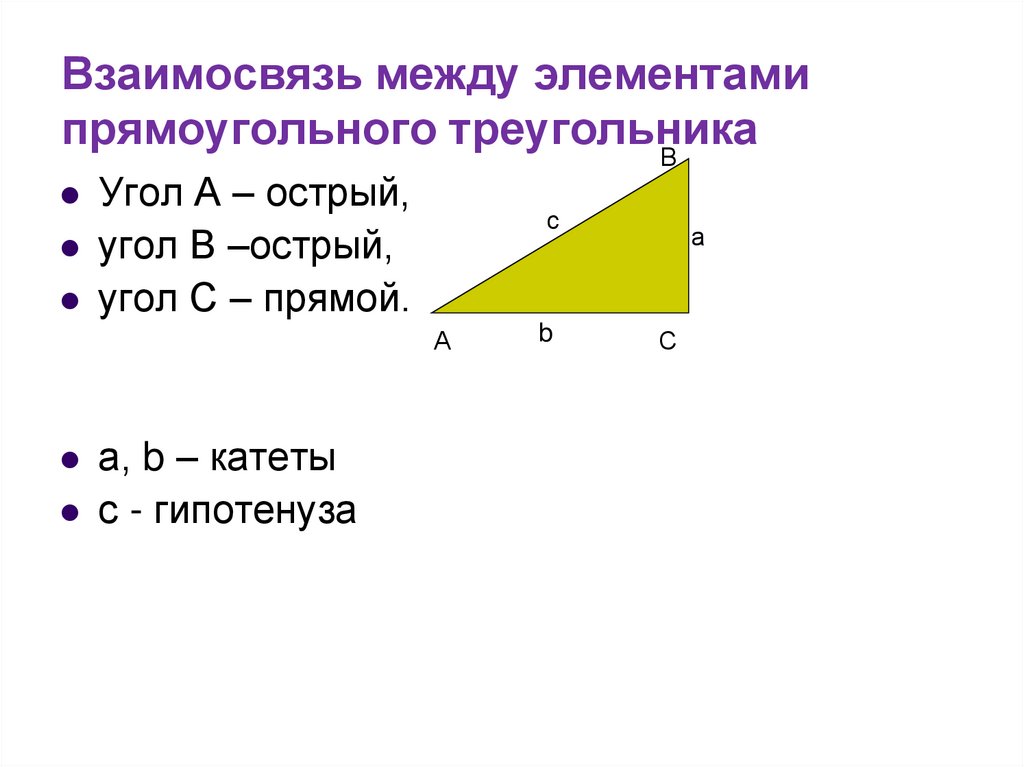
2. Взаимосвязь между элементами прямоугольного треугольника
ВУгол А – острый,
угол В –острый,
угол С – прямой.
с
А
а, b – катеты
с - гипотенуза
b
а
С
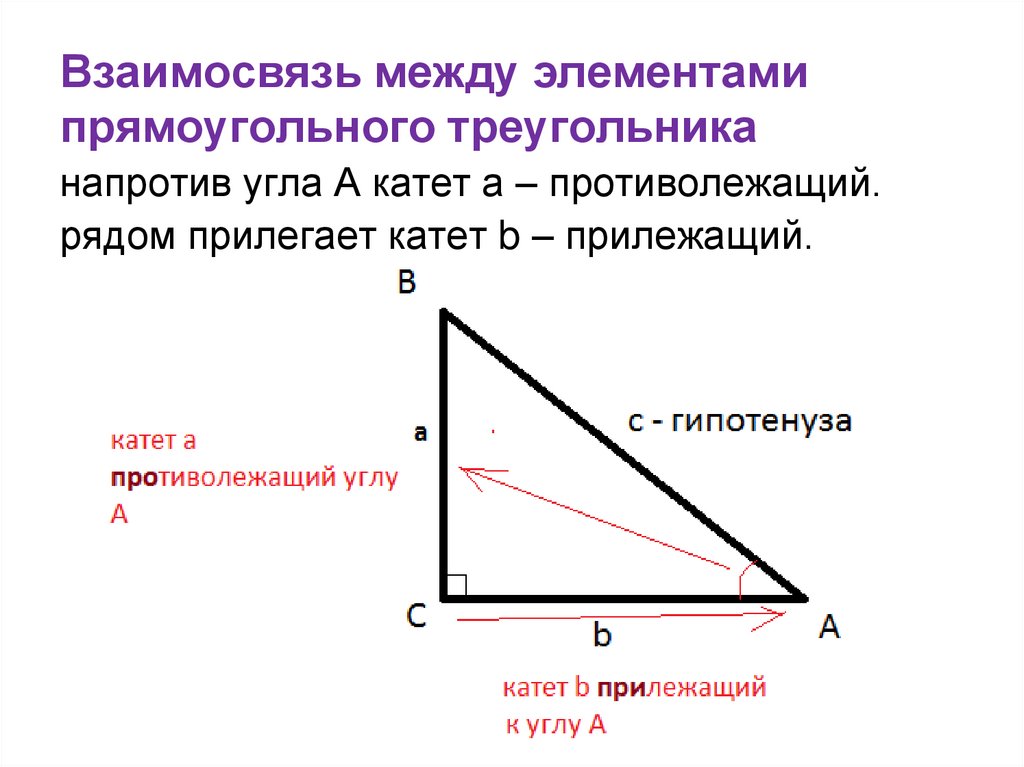
3. Взаимосвязь между элементами прямоугольного треугольника
напротив угла А катет а – противолежащий.рядом прилегает катет b – прилежащий.
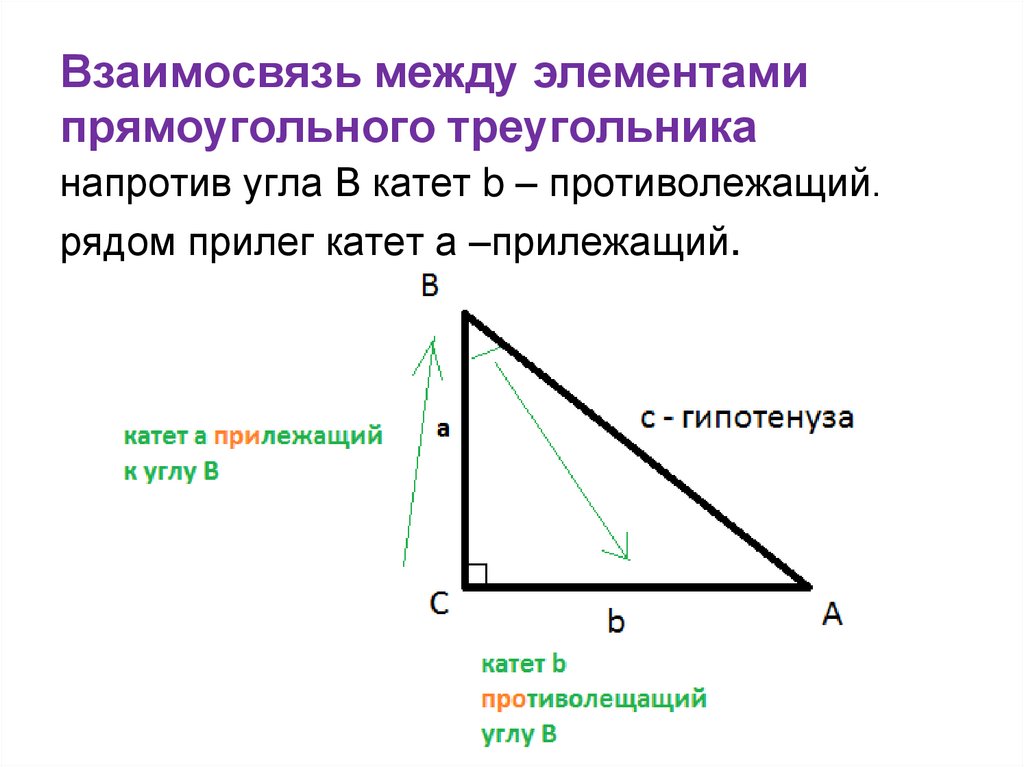
4. Взаимосвязь между элементами прямоугольного треугольника
напротив угла В катет b – противолежащий.рядом прилег катет а –прилежащий.
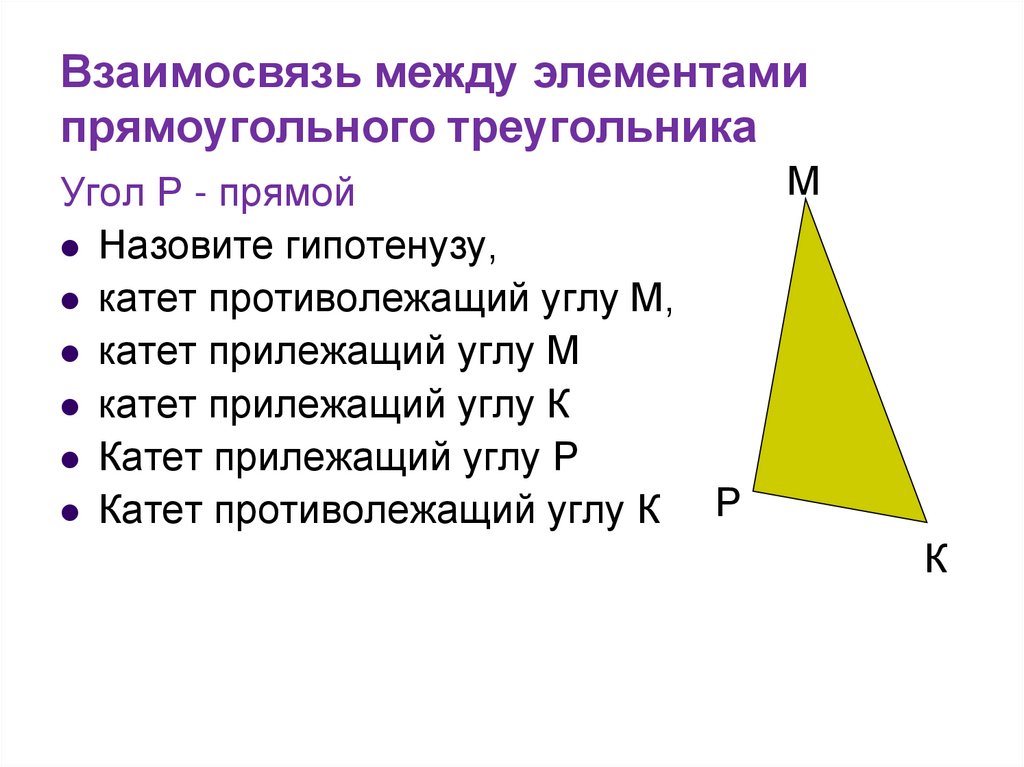
5. Взаимосвязь между элементами прямоугольного треугольника
Угол Р - прямойНазовите гипотенузу,
катет противолежащий углу М,
катет прилежащий углу М
катет прилежащий углу К
Катет прилежащий углу Р
Катет противолежащий углу К
М
Р
К
6.
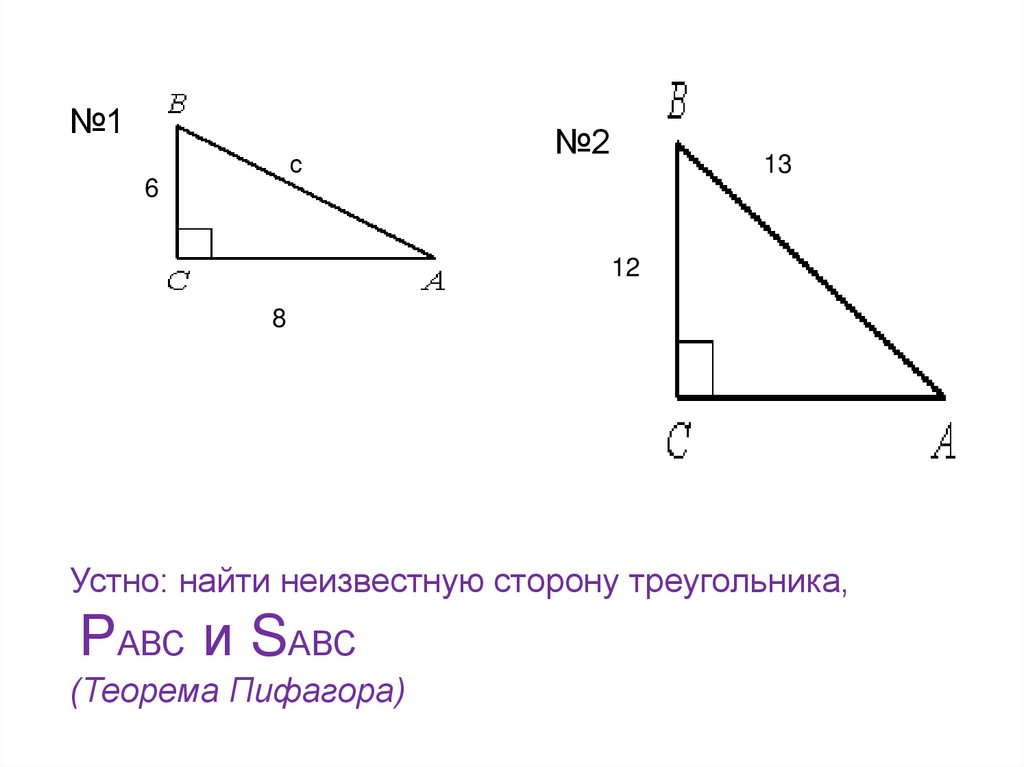
№1с
№2
13
6
12
8
Устно: найти неизвестную сторону треугольника,
РАВС и SАВС
(Теорема Пифагора)
7.
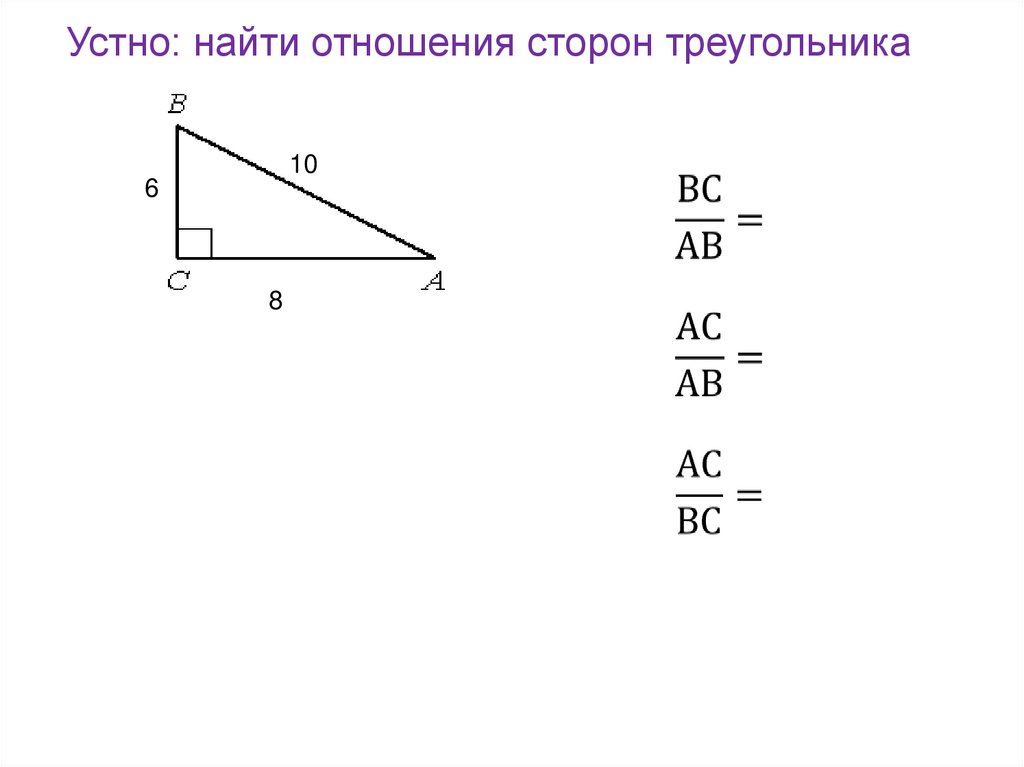
Устно: найти отношения сторон треугольника10
6
8
8. Синус, косинус и тангенс острого угла прямоугольного треугольника
9.
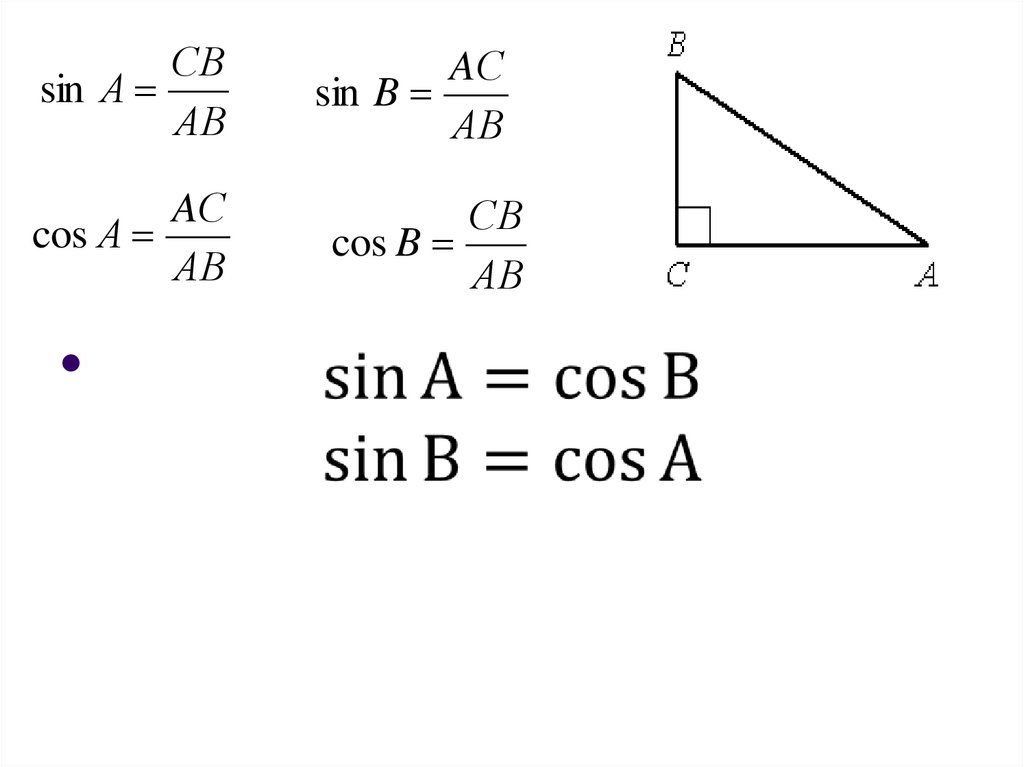
Синусом острого угла прямоугольноготреугольника называется отношение
противолежащего катета к
гипотенузе
СB
sin А
АB
AС
sin B
АB
10.
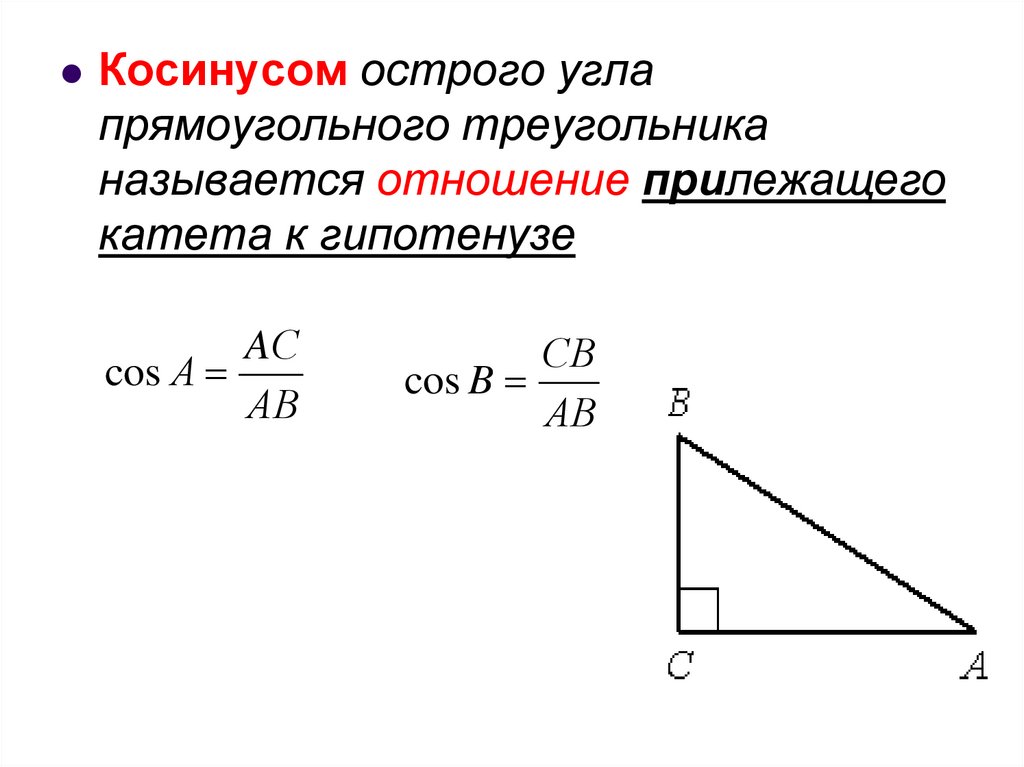
Косинусом острого углапрямоугольного треугольника
называется отношение прилежащего
катета к гипотенузе
AС
cos А
АB
СB
cos B
АB
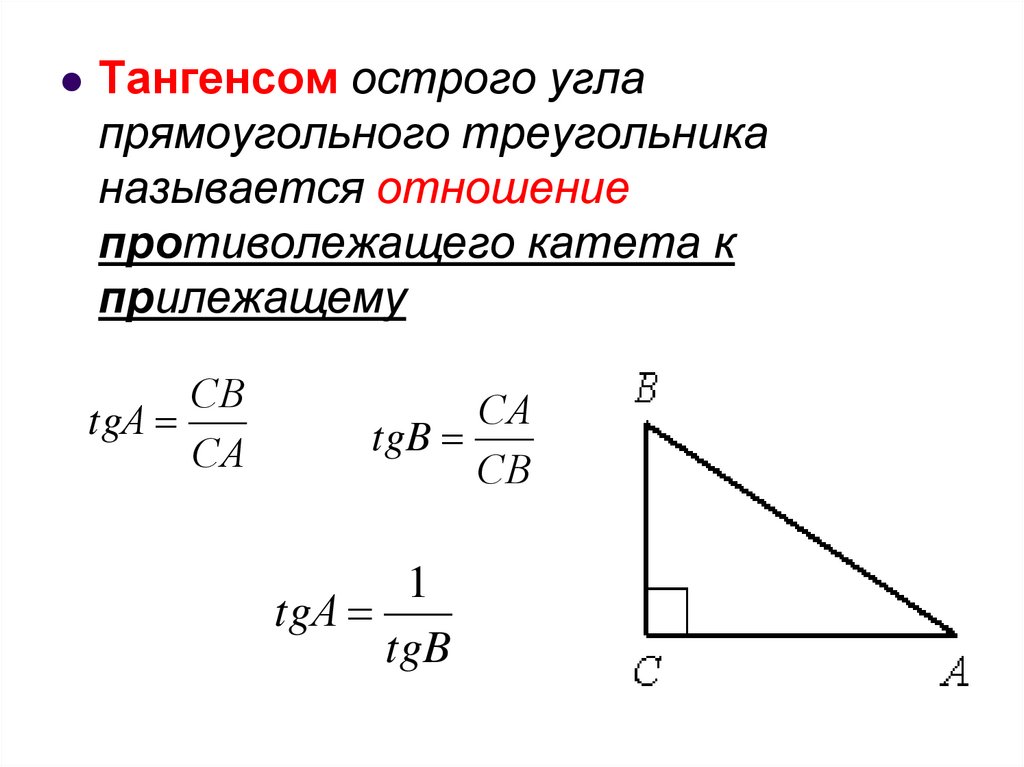
11.
Тангенсом острого углапрямоугольного треугольника
называется отношение
противолежащего катета к
прилежащему
СB
tgА
СA
СA
tgB
СB
1
tgА
tgB
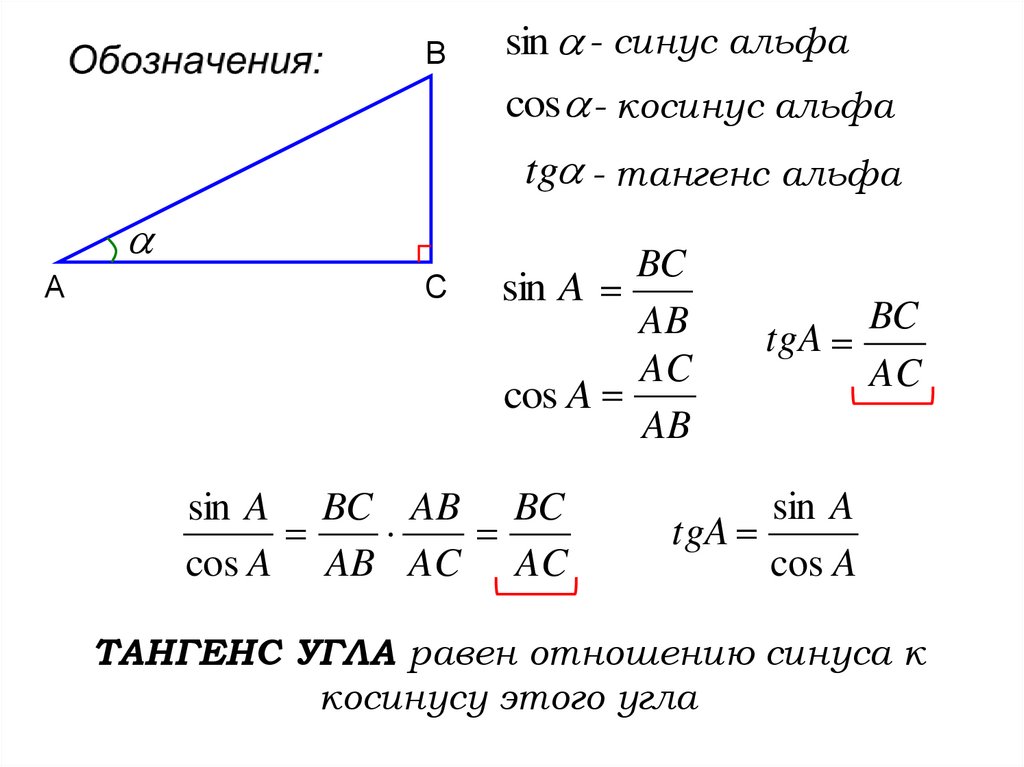
12.
Вsin - синус альфа
cos - косинус альфа
tg - тангенс альфа
А
С
BC
sin A
AB
AC
cos A
AB
sin A BC AB BC
cos A AB AC AC
BC
tgA
AC
sin A
tgA
cos A
ТАНГЕНС УГЛА равен отношению синуса к
косинусу этого угла
13. Тангенс угла равен отношению синуса к косинусу этого угла
sin AtgA
cos A
14. Соотнесите слова стихотворения с данным определением.
Противолежащий катетСинус А =
гипотенуза
Прилежащий катет
Косинус А =
гипотенуза
«Коль не знаешь правил –
минус.
Если знаешь – тебе плюс!
Если «О», то будет синус,
Если «И», то косинус.
15. Вывод:
Острый угол прямоугольного треугольниказависит от гипотенузы, от катетов.
Примечание:
«Зная длины сторон прямоугольного
треугольника можно вычислить его острый
угол. Но для этого надо знать
тригонометрические функции: «синус»,
«косинус»,»тангенс»
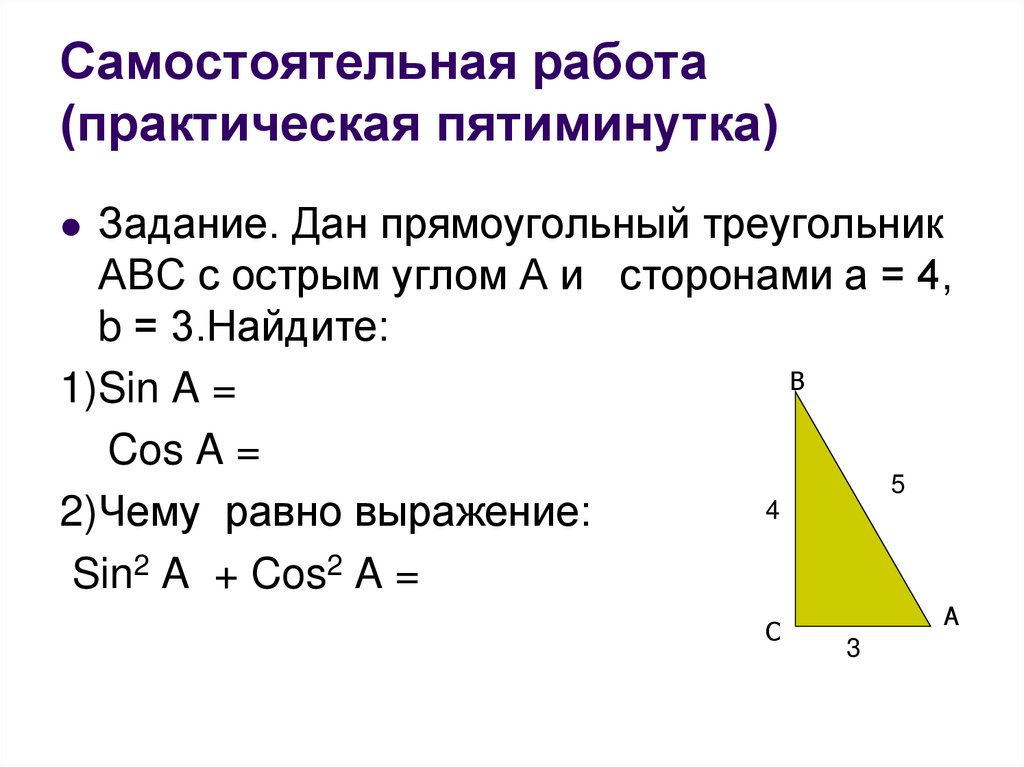
16. Самостоятельная работа (практическая пятиминутка)
Задание. Дан прямоугольный треугольникАВС с острым углом А и сторонами а = 4,
b = 3.Найдите:
В
1)Sin A =
Cos A =
5
4
2)Чему равно выражение:
Sin2 A + Cos2 A =
С
А
3
17. Всегда ли это равенство верное?
1. Ответ: Sin A = 4/5Cos A = 3/5.
2. Ответ: Sin2 A + Cos2 A = 1.
Всегда ли это равенство верное?
18. Основное тригонометрическое тождество
«Тригонометрия» в переводе с греческого«измерение треугольников»19.
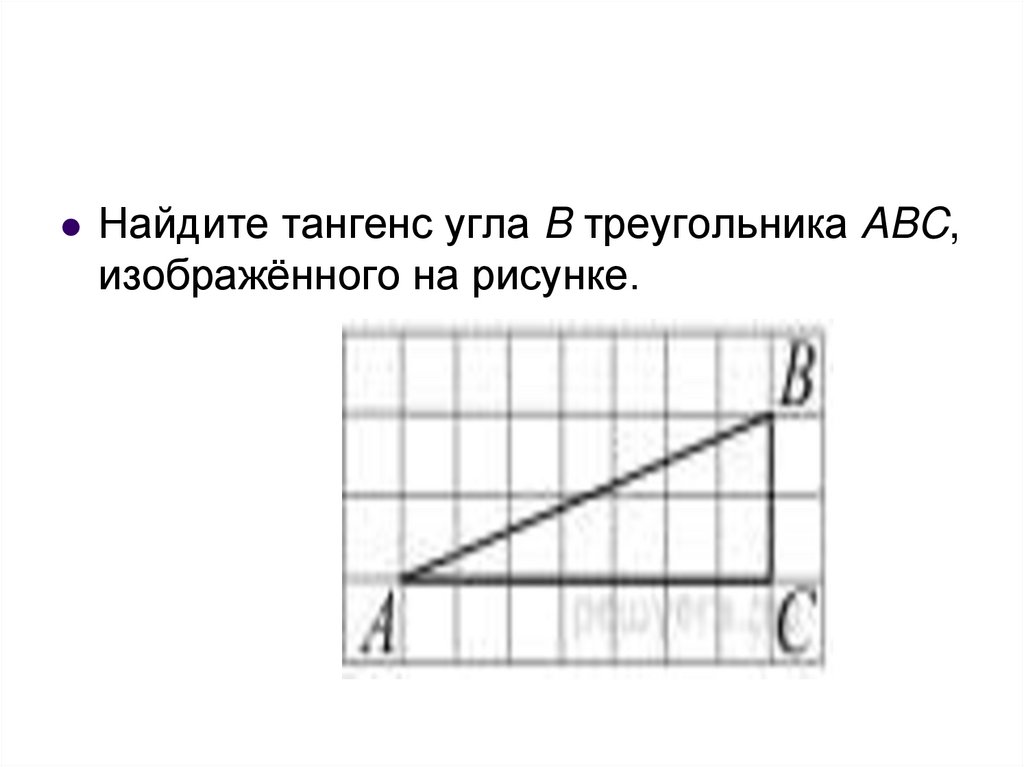
Найдите тангенс угла B треугольника ABC,изображённого на рисунке.
20.
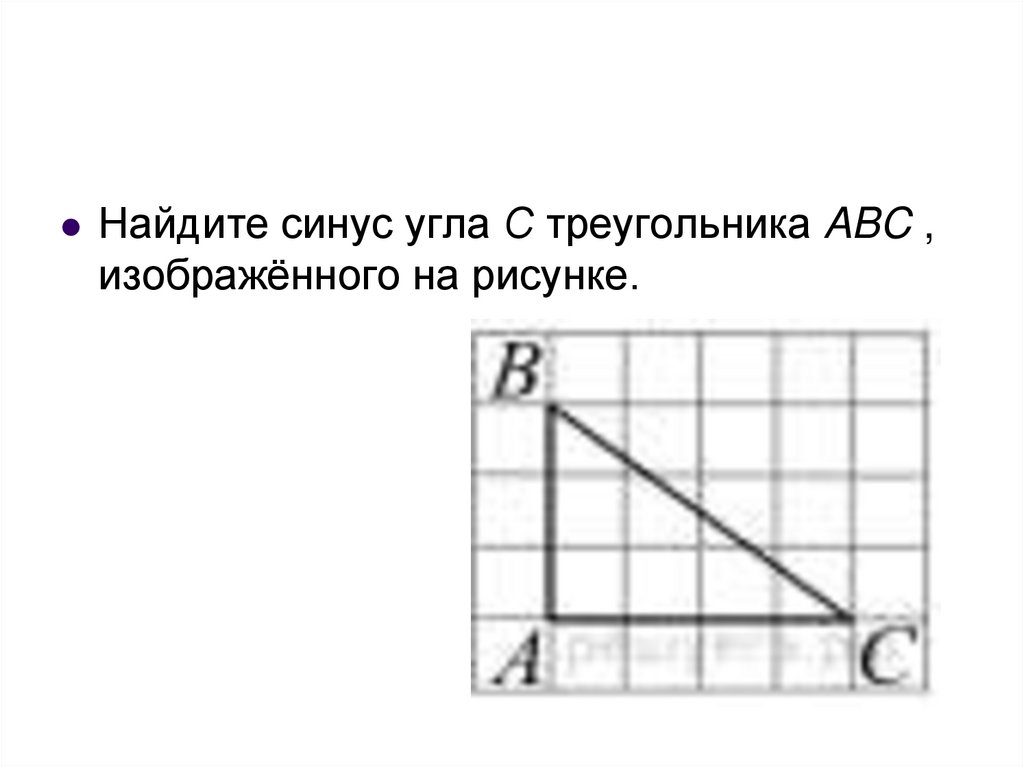
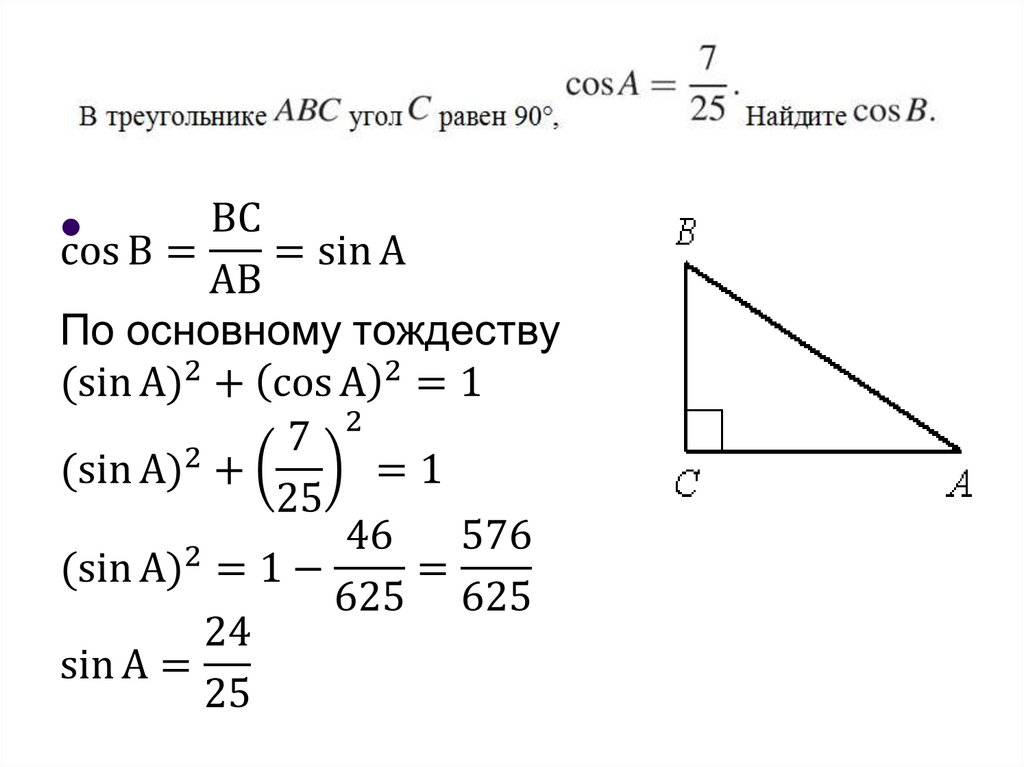
Найдите синус угла С треугольника ABC ,изображённого на рисунке.
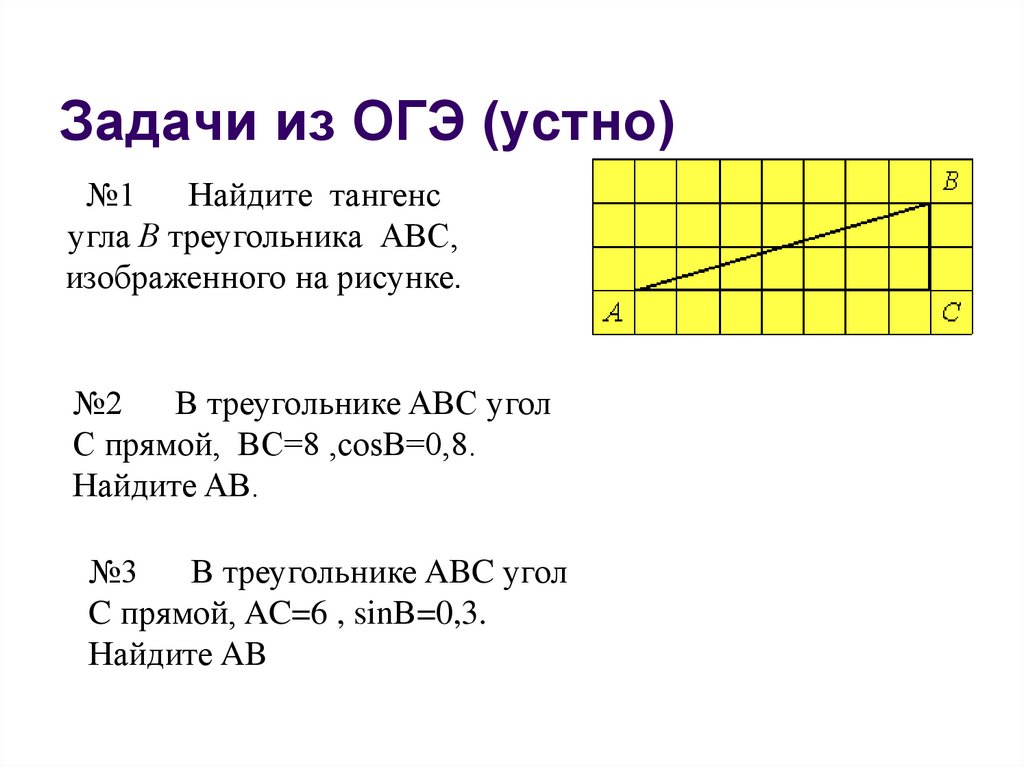
21. Задачи из ОГЭ (устно)
№1Найдите тангенс
угла В треугольника АВС,
изображенного на рисунке.
№2
В треугольнике ABC угол
C прямой, BC=8 ,сosB=0,8.
Найдите AB.
№3
В треугольнике ABC угол
C прямой, AC=6 , sinВ=0,3.
Найдите AB
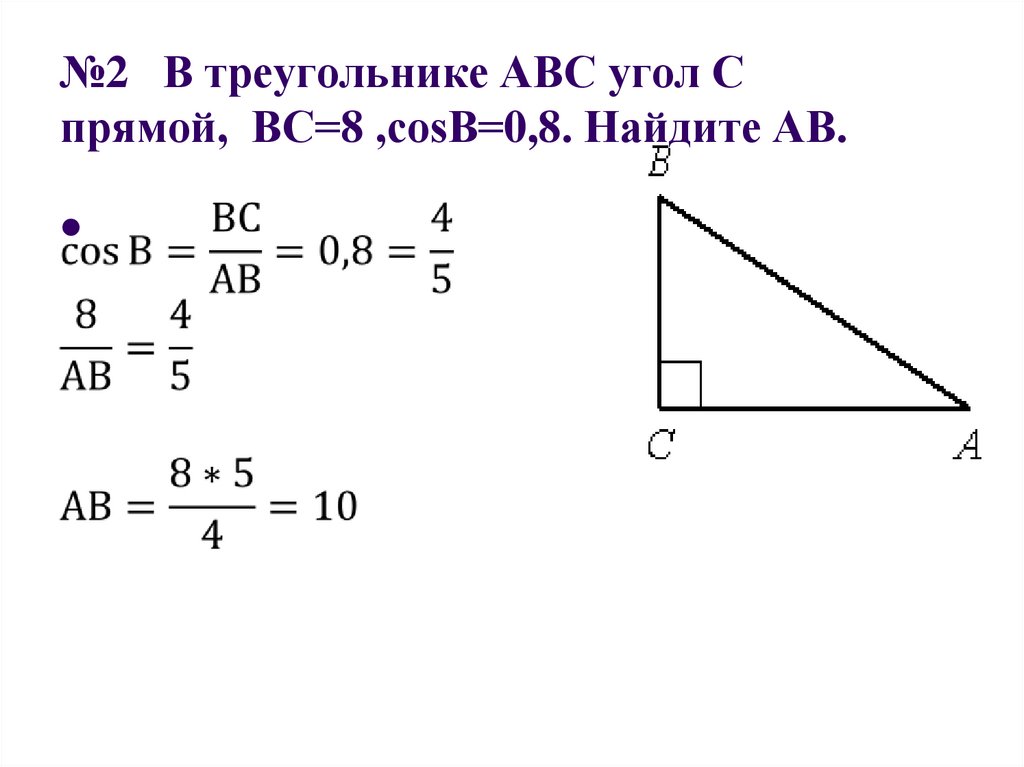
22. №2 В треугольнике ABC угол C прямой, BC=8 ,сosB=0,8. Найдите AB.
23. №3 В треугольнике ABC угол C прямой, AC=6 , sinВ=0,3. Найдите AB
24.
25.
26.
27.
СBsin А
АB
AС
cos А
АB
AС
sin B
АB
СB
cos B
АB
28.
29.
30.
31.
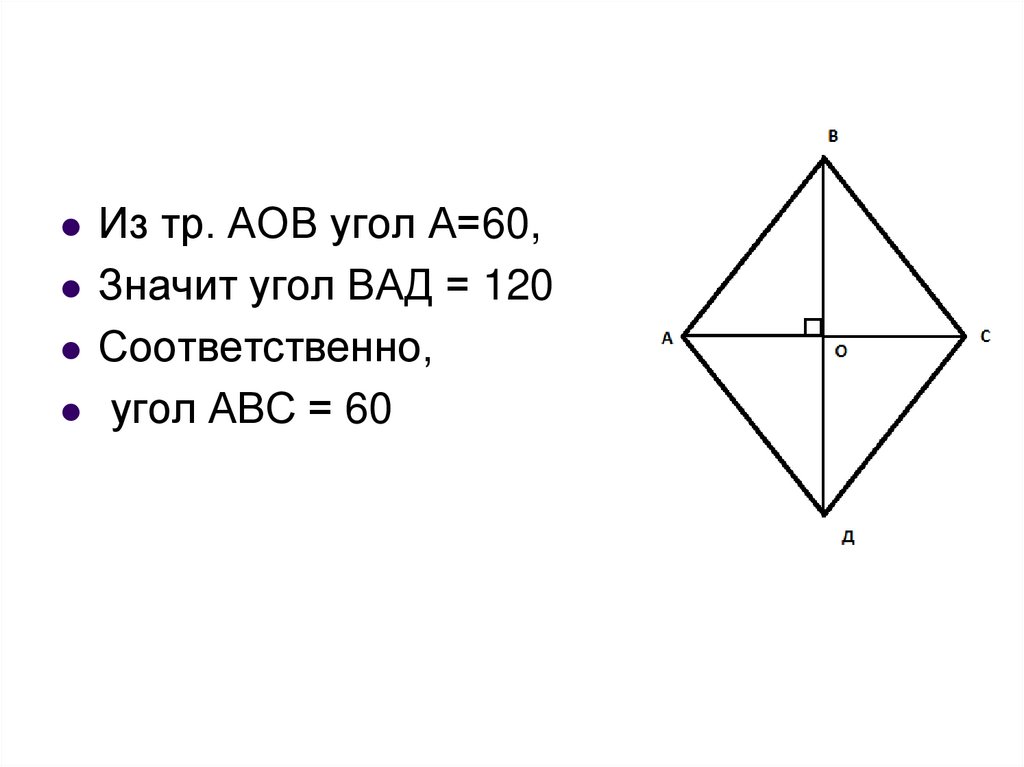
Из тр. АОВ угол А=60,Значит угол ВАД = 120
Соответственно,
угол АВС = 60
32.
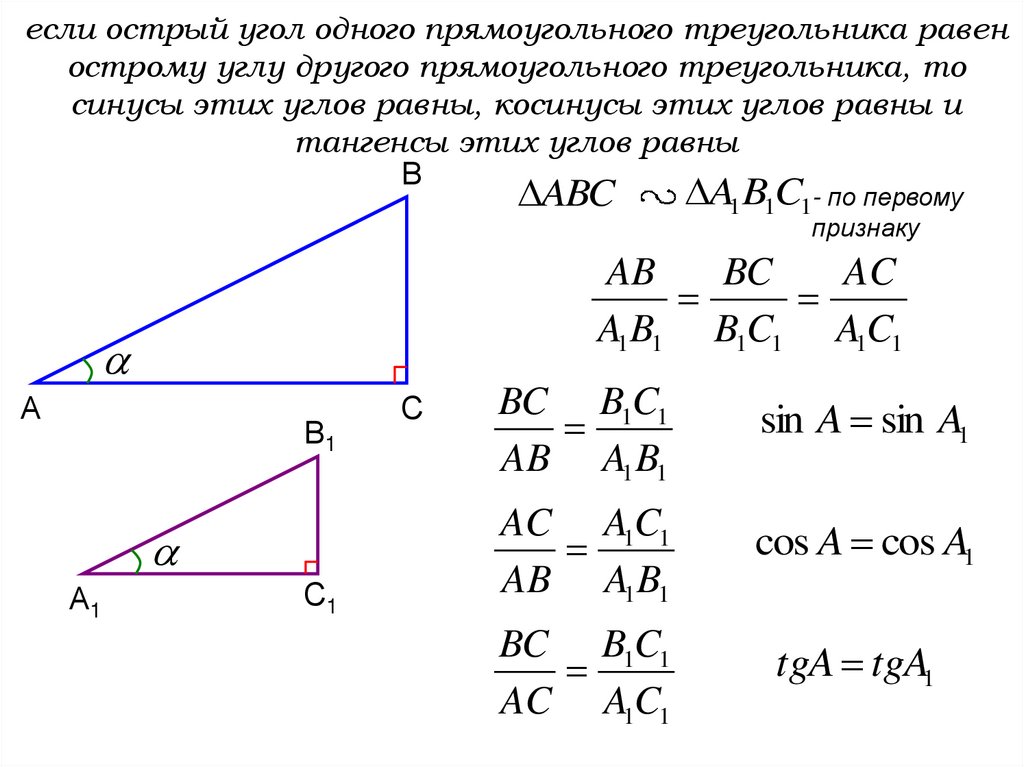
если острый угол одного прямоугольного треугольника равенострому углу другого прямоугольного треугольника, то
синусы этих углов равны, косинусы этих углов равны и
тангенсы этих углов равны
В
ABC
признаку
AB
BC
AC
A1 B1 B1C1 A1C1
А
В1
А1
A1B1C1- по первому
С1
С
BC B1C1
AB A1 B1
sin A sin A1
AC A1C1
AB A1 B1
cos A cos A1
BC B1C1
AC A1C1
tgA tgA1












 Математика
Математика