Похожие презентации:
Возможности восстановления смазанных космических изображений
1.
Возможности восстановлениясмазанных космических
изображений
Б.С. Жуков
Институт космических исследований РАН
2.
Источники «смаза» космических изображений- движение носителя,
- дефокусировка,
- разрешение объектива хуже разрешения фотоприемной
матрицы,
- суб-пиксельное подсканирование (супер-разрешение)
Задача
Устранить смаз
3.
Математическая формулировка задачиМодель формирования цифрового изображения:
g (i, j ) h(x ij x ) f (x )dx n(i, j )
g (i, j ) - цифровое изображение, f (x) - поле яркости,
h( x) - непрерывная функция рассеяния точки (ФРТ) съемочной системы,
n(i, j ) - шум, x ij - координаты центра пиксела (i,j)
где:
Дискретная аппроксимация:
g (i, j ) h(i m, j n) f (m, n) n(i, j )
(1)
m,n
где: f (i, j ) - идеальное изображение (усреднение поля яркости по площади пиксела)
h( i, j ) - дискретная аппроксимация ФРТ
Задача:
Решить уравнение (1) относительно идеального изображения
f (i, j )
4.
Особенность задачизадача решения уравнения
g (i, j ) h(i m, j n) f (m, n)
m,n
относится к классу некорректных задач, решение которых неустойчиво:
при наличии даже небольшого шума возможны большие отклонения
восстановленного изображения от идеального
Методы решения
Классические: решить задачу при заданной ФРТ
Инверсная и винеровская фильтрация, фильтрация
Тихонова, метод Ричардсона-Люси и др.
Слепые: решить задачу при неизвестной ФРТ
5.
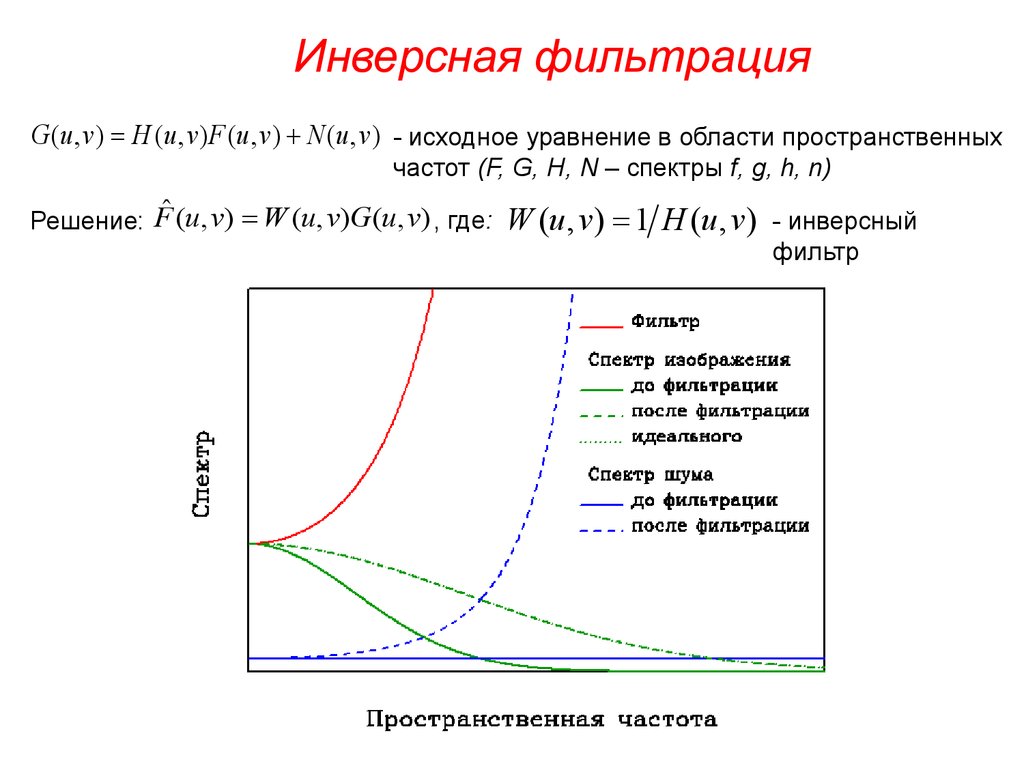
Инверсная фильтрацияG (u, v) H (u , v) F (u, v) N (u , v) - исходное уравнение в области пространственных
частот (F, G, H, N – спектры f, g, h, n)
Решение: Fˆ (u , v) W (u , v)G (u , v) , где:
W (u , v) 1 H (u , v)
- инверсный
фильтр
6.
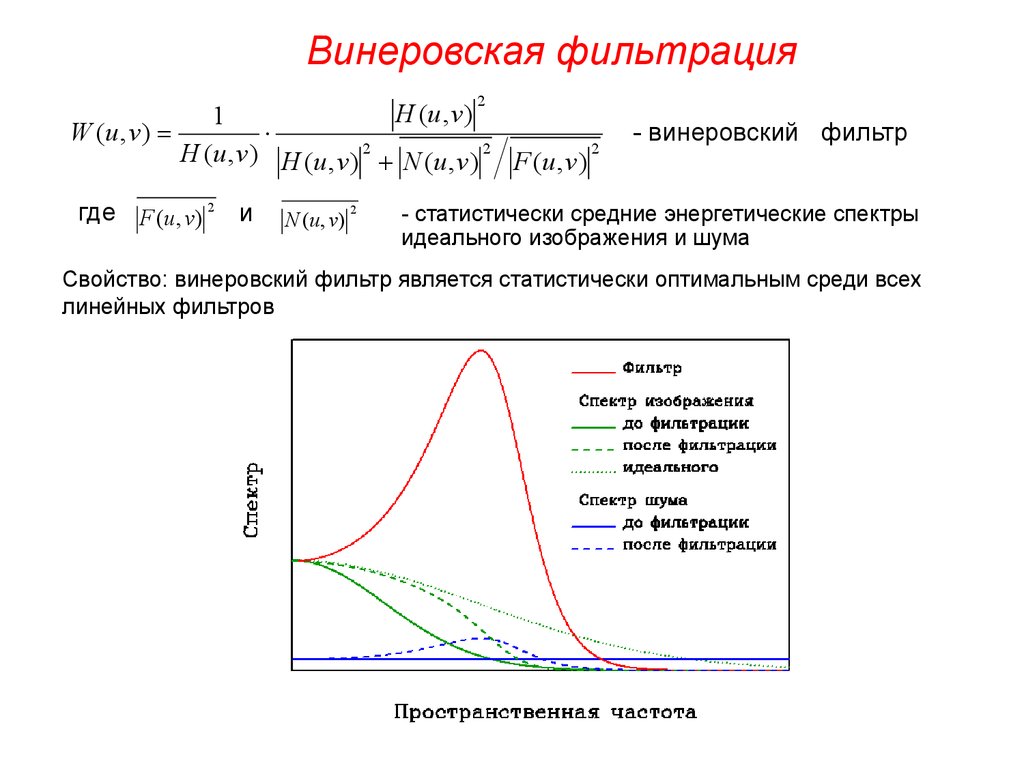
Винеровская фильтрация2
H (u , v)
1
W (u , v)
H (u, v) H (u , v) 2 N (u, v) 2 F (u, v) 2
где F (u, v) 2 и
N (u , v)
2
- винеровский фильтр
- статистически средние энергетические спектры
идеального изображения и шума
Свойство: винеровский фильтр является статистически оптимальным среди всех
линейных фильтров
7.
Фильтрация Тихонова2
H (u, v)
1
W (u, v)
H (u , v) H (u , v) 2 u 2 v 2
- фильтр Тихонова
где α – подбираемый параметр.
При α = 0 фильтрация Тихонова сводится к инверсной фильтрации
8.
Элемент:4 пиксела
Элемент:
1 пиксел
Элемент:
2 пиксела
Элемент:
8 пиксела
Тестовое изображение
9.
Смазанное изображение(ширина ФРТ 2σ = 1,5
пиксела,
СКО шума = 1
ЕМР)
После инверсной фильтрации
10.
Смазанное изображение(ширина ФРТ 2σ = 2 пиксела,
СКО шума = 1 ЕМР)
После инверсной фильтрации
11.
Смазанное изображениеПосле инверсной фильтрации
(ширина ФРТ 2σ = 2,5 пиксела,
СКО шума = 1 ЕМР))
После фильтрации Тихонова
(α = 1.Е-5)
12.
Смазанное изображение(ширина ФРТ 2σ = 3 пиксела,
СКО шума = 1 ЕМР)
После инверсной фильтрации
После фильтрации Тихонова
(α = 6.Е-6)
13.
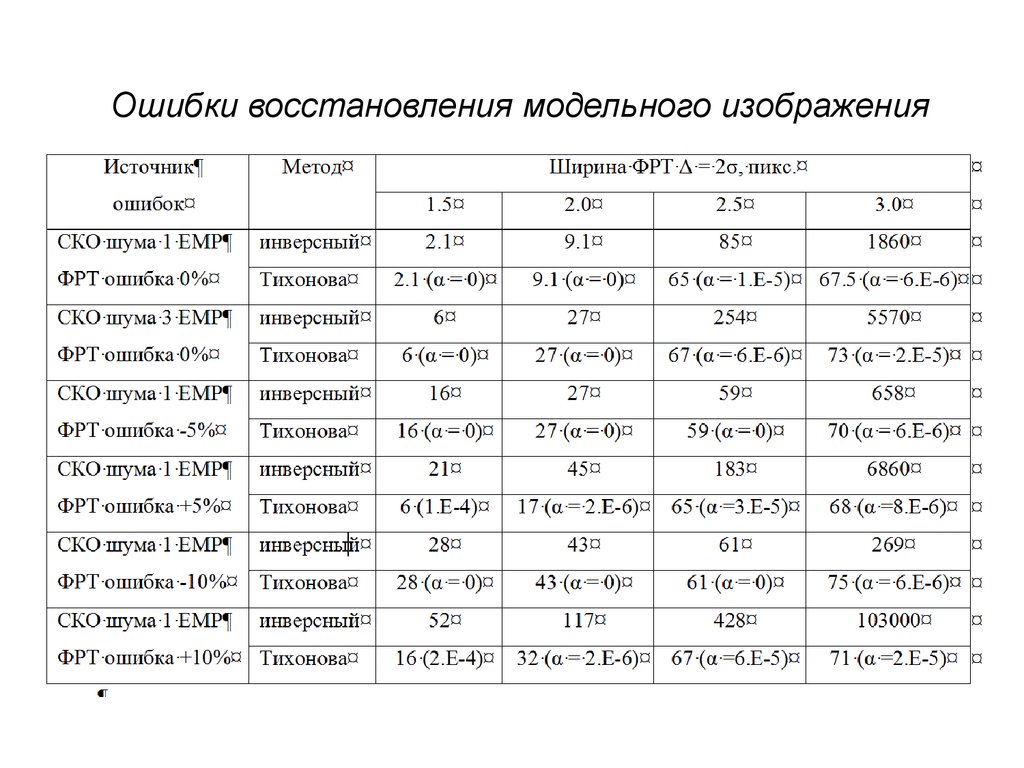
Ошибки восстановления модельного изображения14.
Изображение Луны, полученное УТК-ТСНН (2σx = 1.96, 2σy = 1.70)15.
Изображение Луны после фильтрации Тихонова (α = 1.Е-4)16.
до фильтрациипосле фильтрации
Фрагмент изображения Луны
17.
до фильтрациипосле фильтрации
Фрагмент изображения Луны
18.
ЗаключениеРезультаты анализа тестового изображения
показывают, что при низком уровне шума (1:250 относительно
максимального сигнала) и небольших ошибках в ФРТ (до 5%)
метод Тихонова позволяет удовлетворительно восстановить
объекты размером до половины ширины ФРТ с качеством,
пригодным для визуального анализа.
Метод Тихонова требует подбора параметра α в
зависимости от уровня шума и точности знания ФРТ съемочной
системы и поэтому хорошо подходит для интерактивного
режима обработки изображений.
Возможность использования метода в автоматическом
режиме (например, при потоковой обработки изображений КМСС)
требует дополнительных исследований.















 Физика
Физика








