Похожие презентации:
Дифференциальное исчисление функции одной переменной
1.
ДИФФЕРЕНЦИАЛЬНОЕИСЧИСЛЕНИЕ
ФУНКЦИИ ОДНОЙ
ПЕРЕМЕННОЙ
1
2.
ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ ФУНКЦИИПредел отношения приращения функции y=f(x) к приращению
аргумента (x), когда приращение аргумента ( x) стремится к нулю
(если этот предел существует и является конечным) называется
производной функции
y
f ( x x) f ( x)
lim
lim
f / x
x 0 x
x 0
x
Операция нахождения производной называется дифференцированием.
2
3.
ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙПроизводная функции в точке х0 есть угловой коэффициент
касательной, проведенной к кривой y=f(x) в точке х0.
Уравнение касательной в точке х0:
Y
y y0 f ' x0 x x0
y0
x0
X
Уравнение нормали в точке х0:
1
x x0
y y0 '
f x0
3
4.
ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯПусть функции u(x) и v(x) имеют производные, тогда сумма, разность,
произведение и частное этих функций также имеют производные,
которые выражаются следующим образом:
u v u ' v'
'
u v ' u ' v u v '
u u v u v
2
v
v
'
'
'
Cu Cu'
'
v( x) 0
4
5.
ПРОИЗВОДНАЯ СЛОЖНОЙ ФУНКЦИИПроизводная сложной функции f(g(x)) вычисляется по формуле:
f ( g ( x)) f g g x
5
6.
ТАБЛИЦА ПРОИЗВОДНЫХ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ1)
C' 0
2)
x n x
3)
e e
4)
a a
5)
6)
7)
n '
x '
n 1
x
n 1
u '
x
x '
u n u
e e u
n '
ln a
1
'
ln x
x
u
a a
u '
u
u'
'
ln a u '
1 '
ln u u
u
'
'
1
log a x
x ln a
1
log a u
u'
u ln a
cos x sin x
cos u ' sin u u '
'
, где u u x
'
6
7.
ТАБЛИЦА ПРОИЗВОДНЫХ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ8)
sin x ' cos x
sin u ' cos u u '
9)
tgx '
tgu '
10)
ctgx '
11)
arcsin x '
12)
arccos x '
13)
14)
1
cos 2 x
1
sin 2 x
1
1 x2
1
1 x2
1
arctgx
1 x2
arcctgx ' 1 2
1 x
'
1
'
u
cos 2 u
1
ctgu 2 u '
sin u
arcsin u ' 1 2 u '
1 u
arccos u ' 1 2 u '
1 u
arctgu ' 1 2 u '
1 u
'
1
'
arcctgu
u
1 u2
'
7
8.
ПРИМЕРЫ.1)
3 7
2)
sin x log 3 x sin x log 3 x sin x log 3 x
x
'
4 x 2 3 7 x ln 7 20 x 4 0.
5
'
'
'
1
cos x log 3 x sin x
.
x ln 3
arctgx arctgx ln x arctgx ln x
3)
2
ln x
ln x
1
1
ln x arctgx
2
x.
1 x
2
ln x
'
'
'
8
9.
4)cos x sin x x 2 x sin x .
5)
5x 5x
2
3
'
'
2
1/ 3 '
2 '
2
1
1/ 3 1
'
5 x
5 x
3
5
5
2 / 3
5 x
.
2
3
3
3 25 x
9
10.
ДИФФЕРЕНЦИАЛ ФУНКЦИИПусть y=f(x) определена на промежутке X и дифференцируема в
некоторой окрестности точки x X. Тогда существует конечная
производная
y
lim
f / x
x 0 x
Дифференциалом функции называется главная линейная часть
приращения функции. Дифференциал функции вычисляется по
формуле
d f ( x) f / x dx
10
11.
ПРИМЕРЫ.1) d 4x 1 4 x 1 dx 4dx.
'
2) d sin 3x sin 3x dx 3 cos 3x dx.
'
11
12.
ПРАВИЛО ЛОПИТАЛЯПредел отношения двух бесконечно малых функций или двух
бесконечно больших функций равен пределу отношения их
производных
f x 0
f / x
lim
или lim / .
x x0 g x
x x0 g x
0
12
13.
ПРИМЕРЫ.cos x 1
sin x 0
sin x
1.
1) lim
lim
lim
'
x 0
x 0
1
1
x
0 x 0 x
'
5x 1
5 x 1
5
2) lim
lim
lim
5.
'
x 3 x
x
3 x x 1
'
'
x
a 1 0
a 1
a ln a
3) lim
lim
lim
ln a.
'
x 0
x 0
x
1
0 x 0 x
x
x
13
14.
ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВПроизводную n-го порядка обозначают
f n x .
Аналогично определяются дифференциалы высших порядков.
14
15.
2Пример. ln x 3 .
x
1
'
ln x
x
'' '
'
1
1 '
ln x x 1 x 2
x
''
ln x
'''
x
2x
2 '
3
15







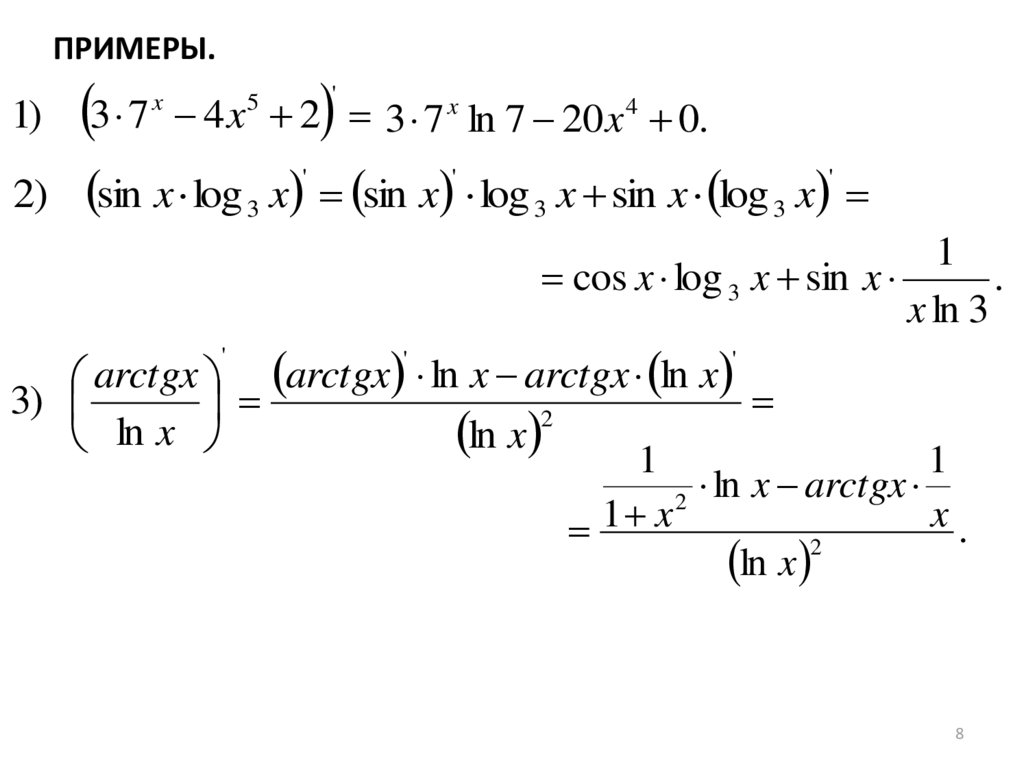
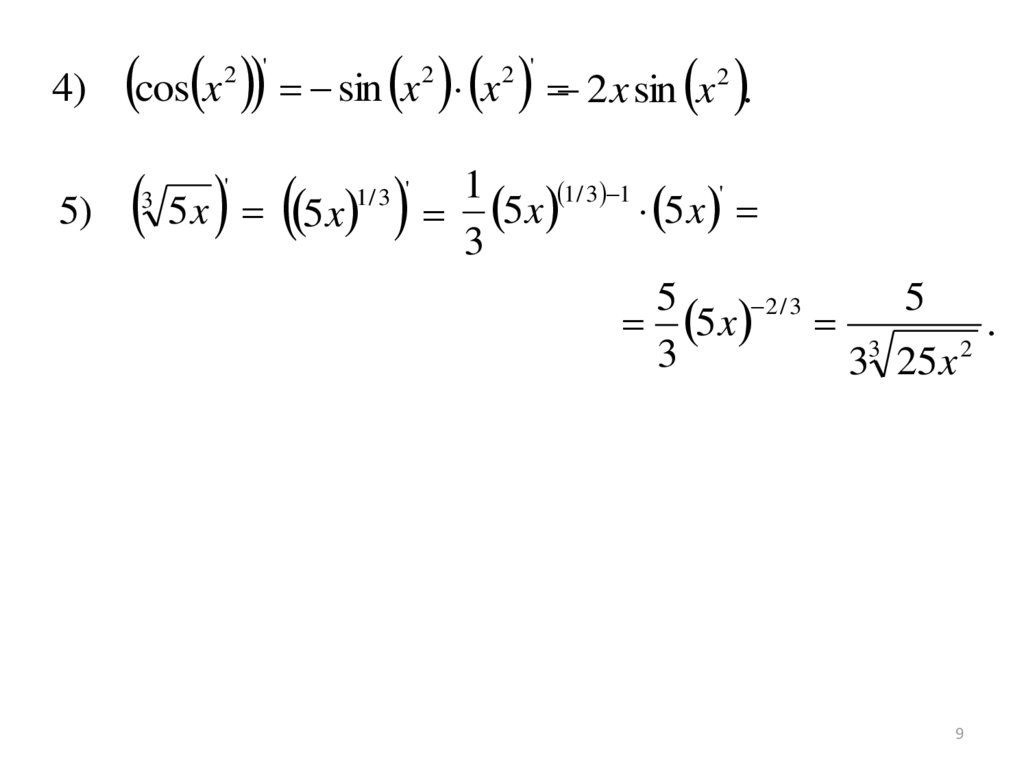

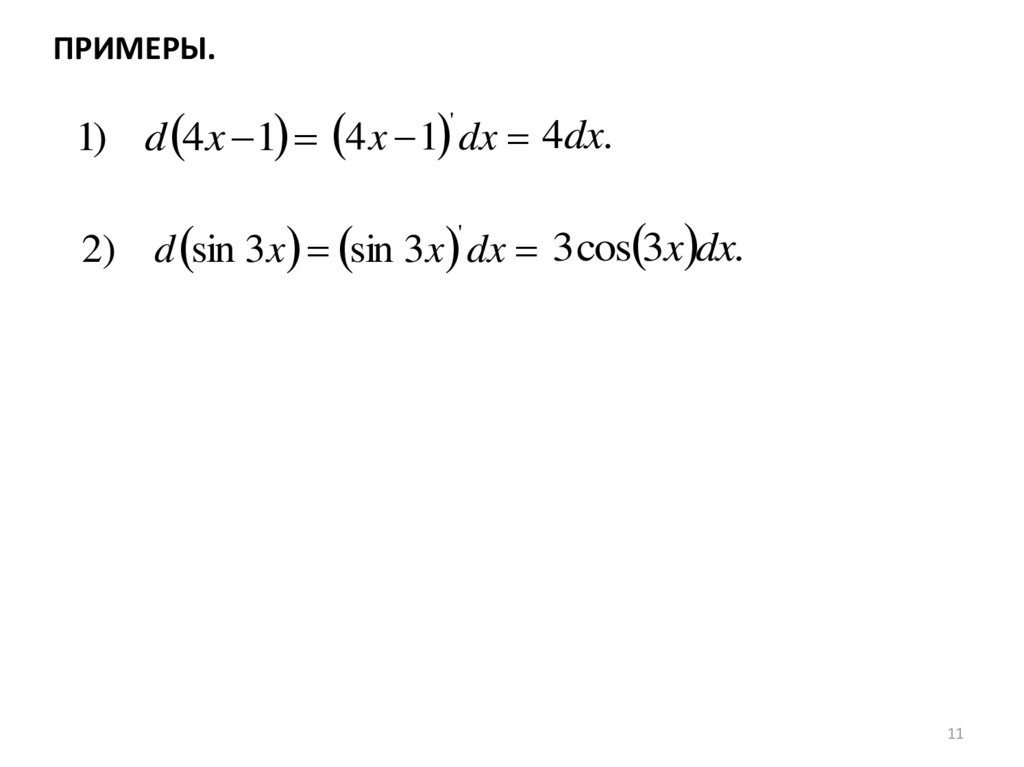



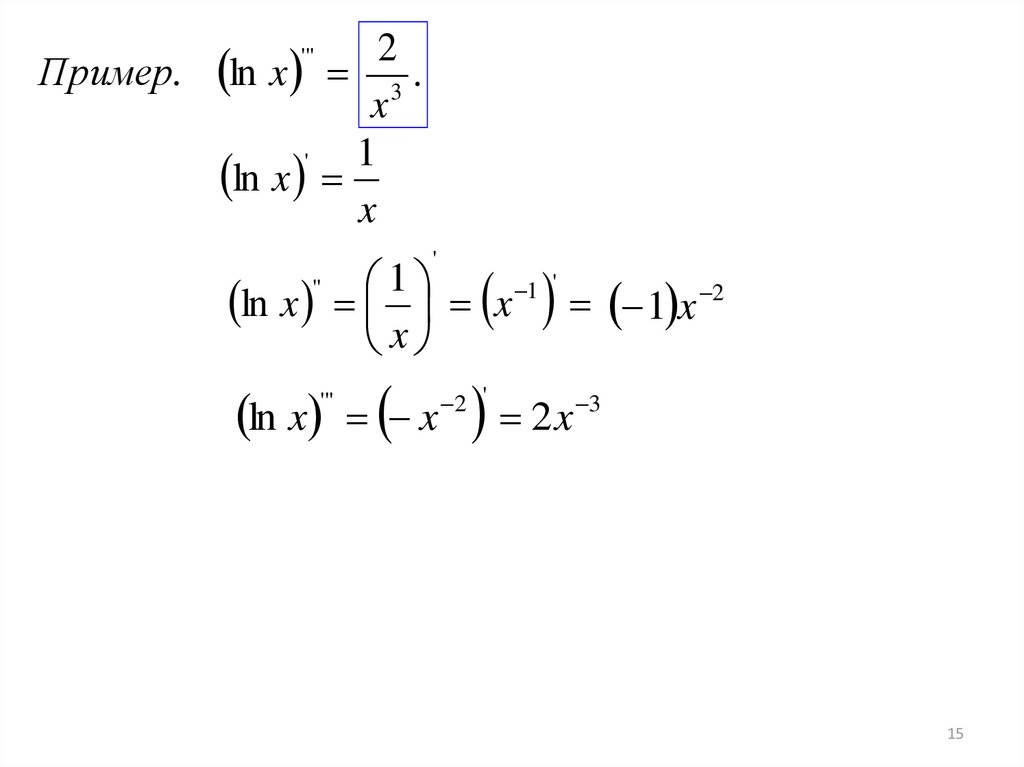
 Математика
Математика








