Похожие презентации:
Предел и непрерывность функции одной переменной
1. Предел и непрерывность функции одной переменной
2. Бесконечно малые функции
Пусть функция (x ) определена в окрестности точки a, кроме, бытьможет, самой точки a.
Функция (x ) называется бесконечно малой функцией
(б.м.ф.) при x, стремящемся к a, если
lim ( x ) 0.
x a
0 0 : x 0 | x a | | ( x) |
3.
Определение б.м.ф. на бесконечностиФункция (x ) называется бесконечно малой функцией
(б.м.ф.) при x , x или x , если
lim ( x) 0
x
lim ( x) 0
x
или
lim ( x) 0
x
4.
Примеры.1. ( x) x 1 б.м.ф. при x 1
lim ( x) lim ( x 1) 0.
x 1
( x) x a
x 1
б.м.ф. при
x a
1
2. ( x) , x 0 б.м.ф. при
x
1
lim ( x) lim 0
x
x x
3. ( x) e x б.м.ф. при
lim ( x) lim e x 0
x
x
x
x
5. Свойства бесконечно малых функций
6. Теорема 5 (сумма б.м.ф.)
Если( x), ( x) - б.м.ф. при x a ,
то их сумма
( x) ( x)
есть также б.м.ф. при
x a.
7.
Доказательство:Функция
(x )
б.м.ф. при x a.
0 1 0 : x a | x a | 1 | ( x) |
2
Функция (x ) б.м.ф. при x a.
0 2 0 : x a | x a | 2 | ( x) |
2
min 1 , 2
x a | x a | | ( x) |
| ( x) |
2
2
| ( x) ( x) | | ( x) | | ( x) |
2 2
( x) ( x) б.м.ф. при x a.
8. Теорема 6 (произведение б.м.ф. на ограниченную функцию)
Если функция (x ) является б.м.ф. при x a,а функция f(x) ограничена в окрестности точки a,
то произведение
есть б.м.ф. при
( x) f ( x)
x a.
9.
Доказательство:f (x )
- ограничена в окрестности точки a.
M 0 1 0
| f ( x) | M x U (a, 1 ) (a 1 , a 1 )
(x ) - б.м.ф. при x a.
0 2 0 : x 0 | x a | 2 | ( x) |
M
min 1 , 2
x 0 | x a | | ( x) |
| f ( x) | M
M
M
| ( x) f ( x) | | ( x) | | f ( x) |
M
x 0 | x a |
( x) f ( x) - б.м.ф. при
x a.
10.
Пример.( x) x
1
y x sin
x
- б.м.ф. при x 0.
1
f ( x) sin , x 0 -ограничена в любой проколотой
окрестности точки x=0.
x
1
y x sin
x
- б.м.ф. при
1
lim x sin 0
x 0
x
x 0.
11.
Следствие.Если
(x )
- б.м.ф. при x a,
а функция f(x) имеет конечный предел
в точке a, то произведение
( x) f ( x) - б.м.ф. при x a.
12.
Лемма.Если функция f(x) в точке x=a имеет предел,
отличный от нуля , то функция
1
- ограничена в окрестности точки x=a.
f ( x)
13.
lim f ( x) A 0Доказательство:
x a
0 0 : x 0 | x a | | f ( x) A |
| A|
2
| A|
| A f ( x) |
2
| A|
| A | | f ( x) | | A f ( x) |
2
| A|
x 0 | x a |
| f ( x ) |
2
1
f ( x)
определена и
1
f ( x)
1
1
2
f ( x) | f ( x) | | A |
- ограничена в проколотой окрестности
точки x=a.
14. Теорема 7
Если (x ) - б.м.ф. приx a,
а функция f(x) в точке x=a имеет предел,
отличный от нуля , то частное
( x ) - есть б.м.ф. при
f ( x)
x a.
15.
Доказательство:( x)
1
( x)
f ( x)
f ( x)
f (x ) имеет конечный предел в точке x=a.
лем м а
1
f ( x)
теорем а6
- ограничена в проколотой окрестности
точки x=a.
1
( x)
f ( x)
- б.м.ф. при x a.
16. Теорема 8(связь функции, имеющей предел, с её пределом и бесконечно малой функцией)
Пусть функция f(x) определена в окрестности точки x=a, кроме,быть может, самой точки a.
Для того, чтобы число А было пределом функции f(x)
при x a , необходимо и достаточно, чтобы f(x) можно
было представить в виде суммы
f ( x) A ( x),
Где (x )
- б.м.ф. при
x a.
lim f ( x) A f ( x) A ( x) : lim ( x) 0
x a
x a
17.
lim f ( x) AНеобходимость.
x a
Положим ( x) f ( x) A
и докажем, что (x ) - б.м.ф. при
x a.
lim f ( x) A
x a
0 ( ) 0 : x, 0 x a f ( x) A
| ( x) |
(x ) - б.м.ф. при x a.
Достаточность.
f ( x) A ( x),
(x ) - б.м.ф. при
lim ( x) 0
x a.
x a
0 ( ) 0 : x, 0 x a ( x)
( x) f ( x) A
| f ( x) A | для тех же значений x .
lim f ( x) A
x a
18. Теорема 9 (арифметические операции над пределами)
Пусть функция f (x ) и (x ) определены в окрестности точки x=a,кроме, быть может, самой точки a.
Если f (x ) и (x ) имеют пределы в точке x=a, то имеют
пределы также их сумма f ( x) ( x), разность f ( x) ( x),
произведение f ( x) ( x) и частное f ( x )
при
( x)
условии lim ( x ) 0 , причём
x a
f ( x) lim ( x)
lim [ f ( x) ( x)] lim
x a
x a
x a
lim [ f ( x ) ( x )] lim f ( x) lim ( x)
x a
x a
x a
lim f ( x )
f
(
x
)
x a
lim
x a
( x)
( x ) lim
x a
(lim ( x) 0)
x a
19.
Доказательство.теорема8
где
lim f ( x) A
x a
f ( x) A ( x),
lim ( x) B
x a
( x) B ( x),
( x), ( x) - б.м.ф. при x a.
f ( x) ( x) [ A ( x)] [ B ( x)]
A B B ( x) A ( x) ( x) ( x)
B (x ), A (x ), ( x) ( x) - б.м.ф. при x a.
( x) B ( x) A ( x) ( x) ( x) - б.м.ф. при x a.
f ( x) ( x) A B ( x)
теорема8
lim [ f ( x) ( x)] A B
x a
20.
Следствие.Постоянный множитель можно выносить за знак
предела.
21. Определение бесконечно большой функции
Пусть функция f (x ) определена в окрестности точки a, кроме, быть может,самой точки a.
Если для любого, как угодно большого, числа M>0
существует такое число , что для всех x a,
удовлетворяющих условию
| x a |
выполняется неравенство
| f ( x) | M ,
То функцию f(x) называют бесконечно большой функцией
при x a.
lim f ( x)
x a
22.
f(x) – б.б.ф.(lim f ( x) )
x a
M 0 (M ) 0 : x, 0 x a
f ( x) M
f(x) – положительная б.б.ф.
(lim f ( x) )
x a
M 0 (M ) 0 : x, 0 x a
f ( x) M
f(x) – отрицательная б.б.ф.
(lim f ( x) )
x a
M 0 (M ) 0 : x, 0 x a
f ( x) M
23.
Пример.Решение.
Функция f ( x)
1
б.б.ф. при х 0, x 0
x
M 0 (M ) 0 : x, 0 x a f ( x) M
1
1
1
| f ( x) |
M | x | | x 0 |
M
x |x|
1
M
1
x 0 | x 0 | | x |
M
1
| f ( x) |
M
|x|
1
1
lim f ( x) б.б. при х 0
x 0 x
x
24. Теорема о связи бесконечно больших и бесконечно малых функций
Если ( x) б.м.ф. при x a и в некоторой окрестноститочки a, кроме, быть может самой точки a, ( x) 0 , то
функция
1
F ( x)
б.б.ф. при х а.
( x)
И, наоборот, если F ( x) б.б.ф. при x a,
.
то
1
( x)
б.м.ф. при х а.
F ( x)
25.
Доказательство.Пусть
( x) б.м.ф. при x a.
Следовательно,
lim ( x) 0
x a
0 ( ) 0 : x, 0 x a
Обозначим
1
1
1
( х)
М
F ( x)
1
( x)
M 0 ( ) 0 : x, 0 x a
lim F ( x)
x a
( x)
F ( x) M
1
F ( x)
б.б.ф. при х а.
( x)
Обратное утверждение доказывается аналогично.
26. Односторонние пределы
Пусть функция f(x) определена только слева (или только справа) от а, т.е. в интервале х< а (х > а).
Определение 1.
Число а называется левосторонним пределом функции f(x)
при
х а (х < а), если
0 ( ) 0 : a x a f ( x) A
lim f ( x) A
x a
lim f ( x) A
x a 0
Определение 2.
Число а называется правосторонним пределом функции
f(x) при х а (х >а), если
lim f ( x) A
x a
lim f ( x) A
x a 0
27.
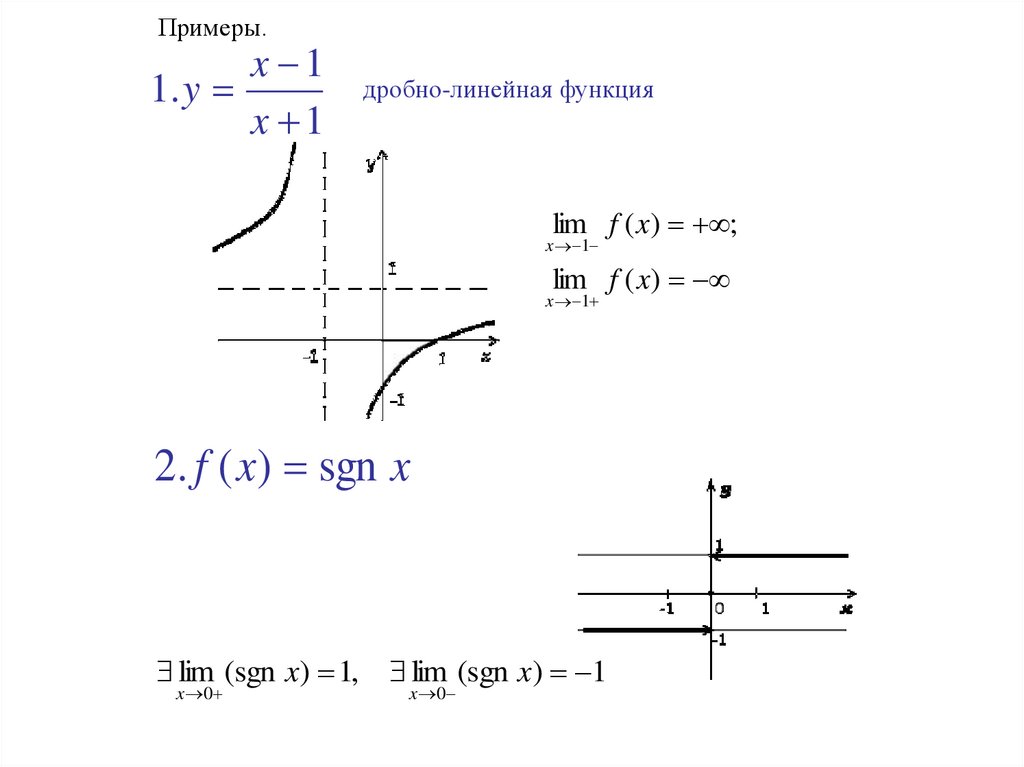
Примеры.x 1
1. y
x 1
дробно-линейная функция
lim f ( x) ;
x 1
lim f ( x)
x 1
2. f ( x) sgn x
lim (sgn x) 1, lim (sgn x) 1
x 0
x 0
28. Теорема
Для того, чтобы функция f(x) имела предел в точке a,необходимо и достаточно, чтобы существовали
пределы функции f(x) в точке a справа и слева и они
были равны между собой.
lim f ( x) lim f ( x) А lim f ( x) A
x a
x a
x a
29.
Доказательство.lim f ( x) A
x a
0 ( ) 0 :
x (a , a ), x a f ( x) A
x (a , a), x a f ( x) A
lim f ( x) A
x a 0
x (a, a ), x a f ( x) A
lim f ( x) A
x a 0
Обратно, lim f ( x) А
x a
lim f ( x) A
x a
0 1 , 2 0 : a x a
f ( x) A
min{ 1 , 2 }
lim f ( x) A
x a
a x a
30. Предел функции (продолжение)
• Бесконечно малые функции.• Сумма б.м.ф., произведение б.м.ф. на
ограниченную, частное б.м.ф. и функции,
имеющей предел в точке.
• Связь функции, имеющей предел, с её пределом и
б.м.ф.
• Арифметические операции над пределами.
• Бесконечно большие функции.
• Связь между б.м.ф. и б.б.ф.
• Односторонние пределы.
















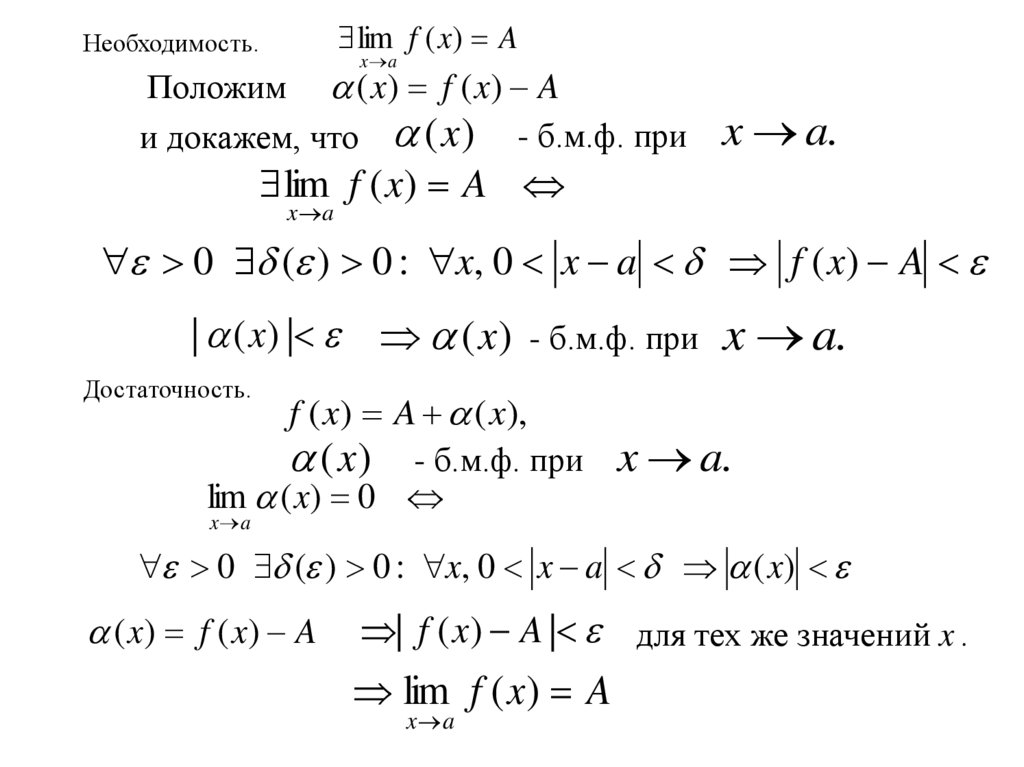










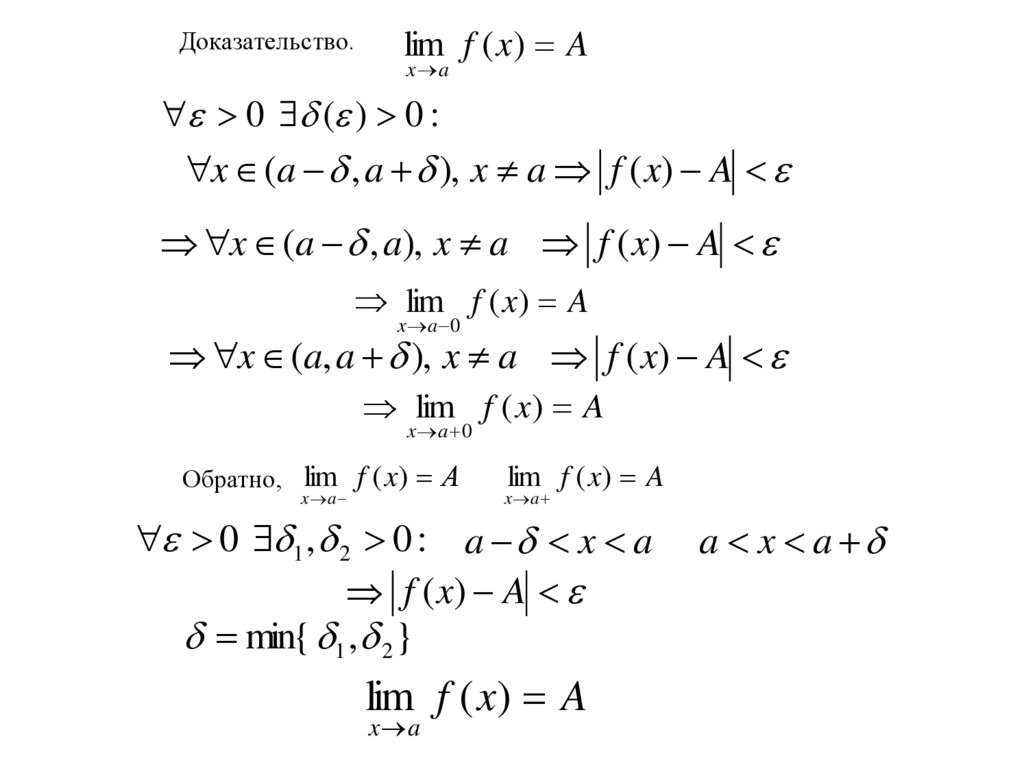

 Математика
Математика








