Похожие презентации:
Определенный интеграл
1.
2.
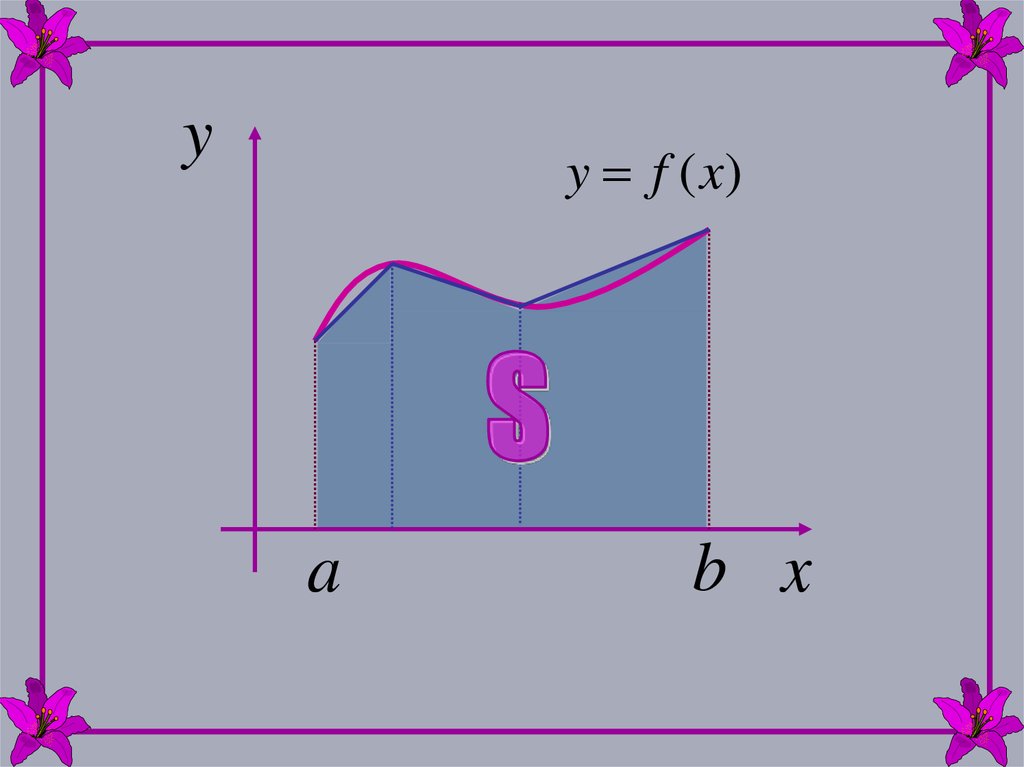
Пустьна
отрезке
[a,b]
задана
неотрицательная функция y=f(x).
Требуется найти площадь криволинейной
трапеции, ограниченной кривой y=f(x),
прямыми x=a, x=b и осью абсцисс y=0.
Рассмотрим
ломаную,
расположенную
достаточно близко к кривой.
3.
Фигура под ломаной состоит из трапеций иее площадь равна сумме площадей всех
трапеций:
S Sтрап
Причем,
площадь
под
кривой
будет
приближенно равна площади под ломаной,
если ломаная достаточно близко подходит к
кривой.
4.
yy f (x)
a
b x
5.
За искомую площадь под кривой берутпредел площади под ломаной при условии,
что ломаная неограниченно приближается
к кривой.
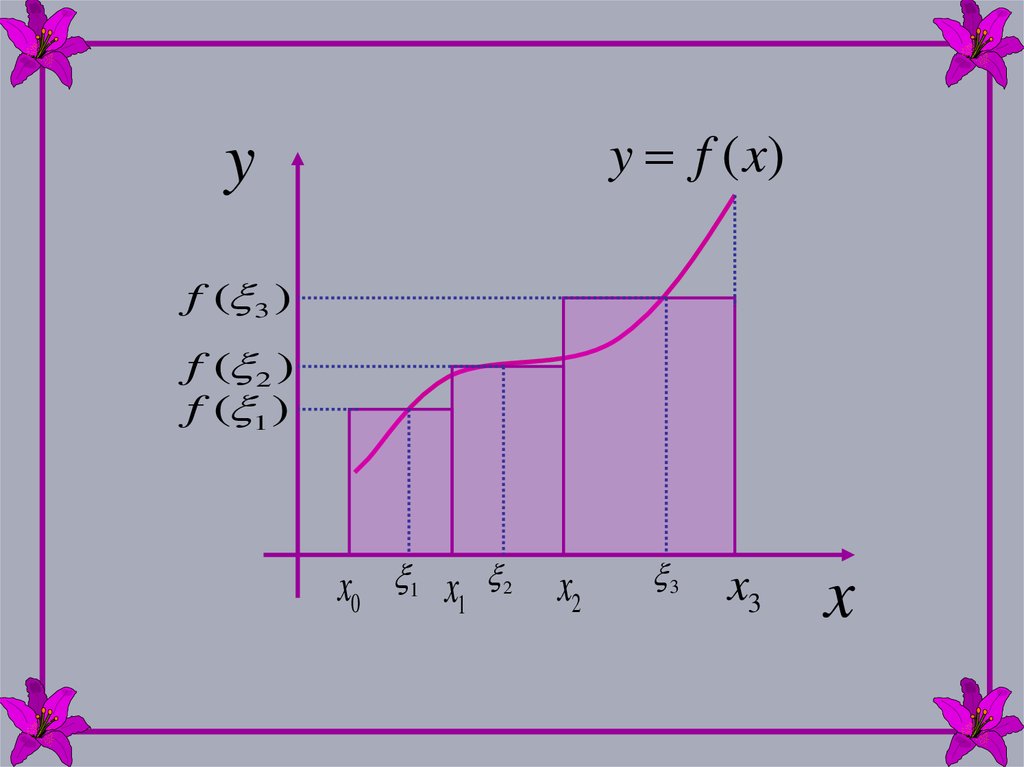
Разобьем отрезок [a,b] на n элементарных
отрезков точками х0, х1, …хn .
Положим
xi xi xi 1
На каждом из отрезков выберем точку ξi , и
найдем значение функции в этой точке
f ( i )
6.
Сумму видаn
f ( ) x
i 1
i
i
называют интегральной суммой
для функции y=f(x) на отрезке [a,b] .
7.
Интегральная сумма зависит от способаразбиения отрезка и выбора точек ξi
Каждое отдельное слагаемое в интегральной
сумме
f ( i ) xi
равно площади
сторонами
прямоугольника
Si
f ( i )
и
xi
со
8.
y f (x)y
f ( 3 )
f ( 2 )
f ( 1 )
x0 1 x1
2
x2
3
x3
x
9.
Наибольший из отрезков разбиенияxi 1 , xi
обозначим как
max xi
Вся интегральная сумма будет равна
n
S Si
i 1
10.
Еслисуществует
конечный
предел
интегральной суммы при max xi 0
не зависящий от способа разбиения отрезка
[a,b] и выбора точек ξi, то он называется
определенным интегралом от функции
y=f(x) на отрезке [a,b].
b
n
lim
max xi 0
f ( ) x f ( x)dx
i 1
i
i
a
11.
Функция y=f(x) называется интегрируемойна отрезке [a,b].
Числа a и b называются нижним и верхним
пределом, соответственно.
12.
Неопределенный интегралf ( x)dx
есть семейство функций, а определенный
b
интеграл
f ( x)dx
a
есть определенное число.
По определению предполагается, что а < b.
Положим
b
a
a
b
f ( x)dx f ( x)dx
13.
С учетом этого несущественно, какой пределбольше или меньше.
Если а = b, то
a
a
a
a
f ( x)dx f ( x)dx
a
2 f ( x)dx 0
a
a
f ( x)dx 0
a
14.
Интегрируемая на отрезке [a,b] функцияy=f(x) ограничена на этом отрезке.
15.
Если на отрезке [a,b] функция y=f(x)непрерывна, то она интегрируема на
этом отрезке.
16.
1Постоянный множитель можно выносить
за знак определенного интеграла.
b
b
a
a
k f ( x)dx k f ( x)dx
17.
Пусть фиксировано разбиение отрезка [a,b] ивыбор точек
1 , 2 ... n
Рассмотрим интегральную сумму:
n
k f ( ) x
i 1
i
i
n
k f ( i ) xi
i 1
Переходим к пределу в левой и правой части
равенства при
max x 0
i
18.
nlim
max xi 0
k f ( ) x
i
i 1
i
k lim
n
lim k f ( i ) xi
max xi 0
max xi 0
i 1
n
f ( ) x
i
i 1
i
Следовательно по определению:
b
b
a
a
k f ( x)dx k f ( x)dx
19.
2Определенный интеграл от алгебраической
суммы (разности) двух функций равен
сумме (разности) интегралов от
этих функций.
b
b
b
a
a
a
f ( x) g ( x) dx f ( x)dx g ( x)dx
20.
3Если отрезок интегрирования разбит
на части, то интеграл на всем отрезке
равен сумме интегралов по каждому
из участков разбиения.
b
c
b
a
a
c
f ( x)dx f ( x)dx f ( x)dx
21.
Геометрически это означает, что если a<c<b ифункция y=f(x) неотрицательна на [a,b], то
согласно
геометрическому
смыслу
определенного интеграла
b
c
b
f ( x)dx S f ( x)dx S f ( x)dx S
1
a
a
S1 S2 S
c
2
22.
yy f (x)
1
a
2
c
b x
23.
4f ( x) g ( x)
Если на [a,b], где a<b,
то
b
b
a
a
f ( x)dx g ( x)dx
24.
Пусть фиксировано разбиение отрезка [a,b] ивыбор точек 1 , 2 ... n
Если
f ( x) g ( x) то для интегральных сумм:
n
n
f ( ) x g ( ) x
i
i 1
i
i 1
i
i
Переходим к пределу в левой и правой части
неравенства при max xi 0
n
lim
max xi 0
f ( ) x
i
i 1
i
lim
max xi 0
b
b
a
a
n
g ( ) x
i 1
f ( x)dx g ( x)dx
i
i
25.
Пусть на [a,b], где a<b,m f ( x) M
где m и M некоторые числа. Тогда
b
m(b a) f ( x)dx M (b a)
a
26.
По свойству 4 имеем:b
b
b
a
a
a
mdx f ( x)dx Mdx
По свойству 1 и геометрическому смыслу
определенного интеграла:
b
mdx m(b a)
a
b
Mdx M (b a)
a
b
m(b a) f ( x)dx M (b a)
a
27.
5Если на [a,b], где a<b, функция y=f(x)
непрерывна, то найдется такое значение
a, b
что
b
f ( x)dx f ( ) (b a)
a
28.
По свойству функции, непрерывной на отрезке,для произвольного значения
x [ a, b]
справедливо неравенство:
m f ( x) M
Где m и М – наименьшее и наибольшее значения
функции на отрезке. Тогда
29.
bm(b a) f ( x)dx M (b a)
a
b
1
m f ( x)dx
M
b a
a
Но функция, непрерывная на отрезке, принимает
любое значение, заключенное
между ее
наименьшим и наибольшим значениями, поэтому
найдется такое число
a, b
что
b
f ( x)dx f ( ) (b a)
a
30.
Пустьf ( x) 0
Тогда теорема о среднем утверждает, что найдется
такая точка
a, b
что площадь под кривой y=f(x) на [a,b] равна
площади прямоугольника со сторонами
f ( ) и (b a)
31.
yy f (x)
f ( )
a
b x
32.
Равенствоb
f ( x)dx f ( ) (b a)
a
называется формулой среднего значения.
f ( )
называется средним значением функции.
33.
6Если
на
[a,b]
функция
y=f(x)
неотрицательна, то площадь под этой
кривой численно равна определенному
интегралу
b
f ( x)dx S
a































 Математика
Математика








