Свойство углов при основании равнобедренного треугольника

1. Свойство углов при основании равнобедренного треугольника

Девиз урока:
Думать – коллективно,
Работать – оперативно,
Спорить – доказательно,
Для всех обязательно!
Свойство углов при основании
Равнобедренный треугольник
равнобедренного треугольника

2.

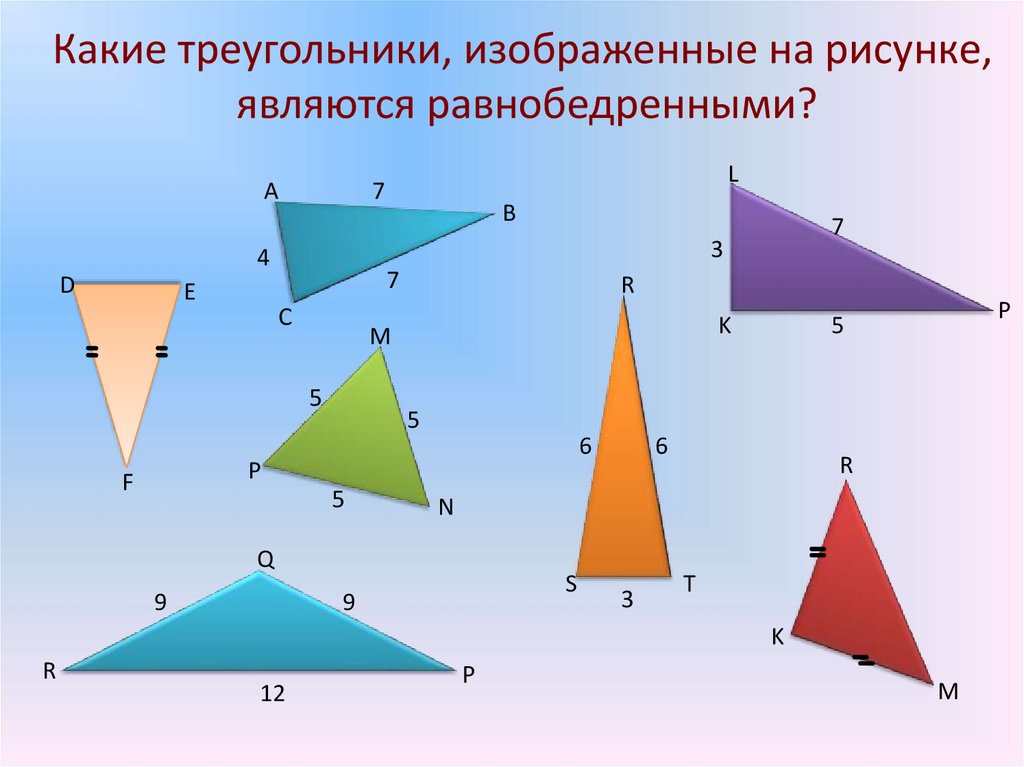
Какие треугольники, изображенные на рисунке,
являются равнобедренными?
А
E
В
7
С
R
K
M
5
6
5
6
R
N
Q
9
P
5
5
P
F
7
3
4
D
L
7
S
9
3
T
K
R
12
P
M

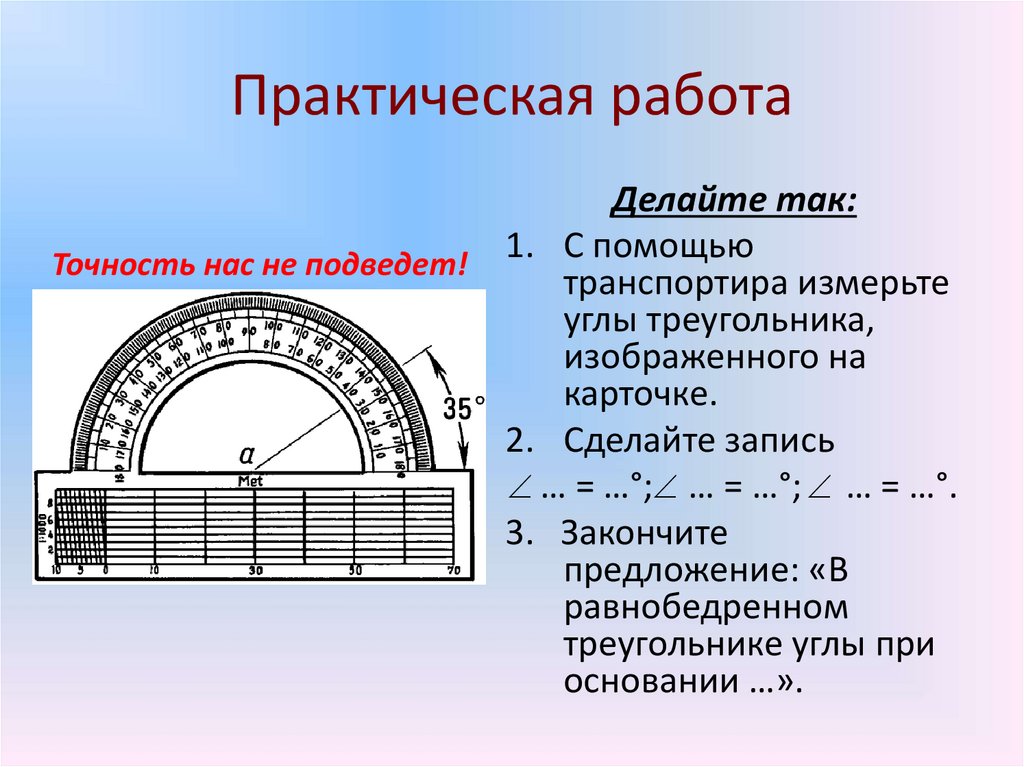
3. Практическая работа

Делайте так:
1. С помощью
Точность нас не подведет!
транспортира измерьте
углы треугольника,
изображенного на
карточке.
2. Сделайте запись
… = …°; … = …°; … = …°.
3. Закончите
предложение: «В
равнобедренном
треугольнике углы при
основании …».

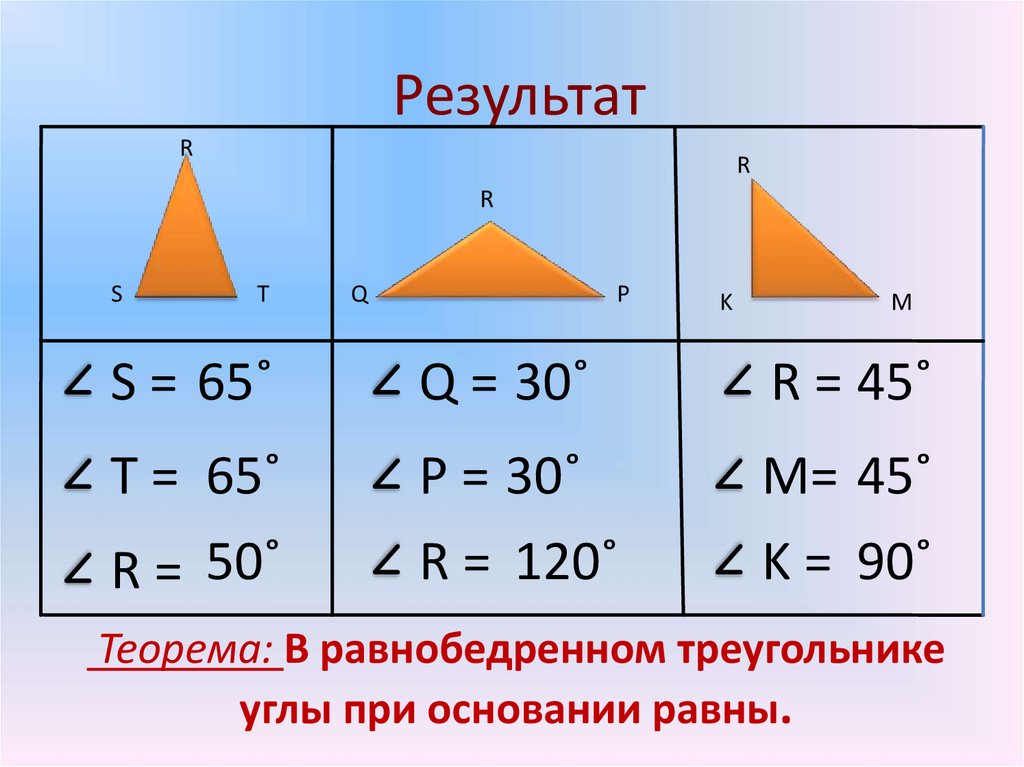
4. Результат

R
R
R
S
T
Q
P
K
M
S = 65˚
Q = 30˚
R = 45˚
T = 65˚
P = 30˚
M= 45˚
R = 50˚
R = 120˚
K = 90˚
Теорема: В равнобедренном треугольнике
углы при основании равны.

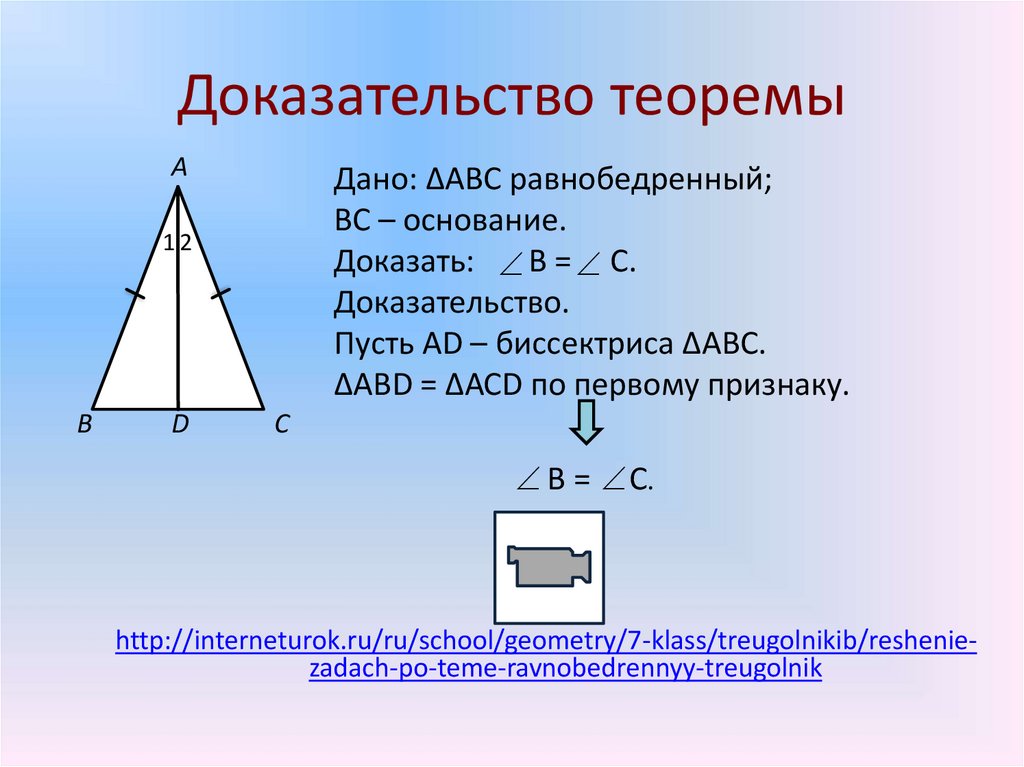
5. Доказательство теоремы

А
Дано: ΔАВС равнобедренный;
ВС – основание.
Доказать: В = С.
Доказательство.
Пусть АD – биссектриса ΔАВС.
ΔАВD = ΔАСD по первому признаку.
12
В
D
С
В = С.
http://interneturok.ru/ru/school/geometry/7-klass/treugolnikib/resheniezadach-po-teme-ravnobedrennyy-treugolnik

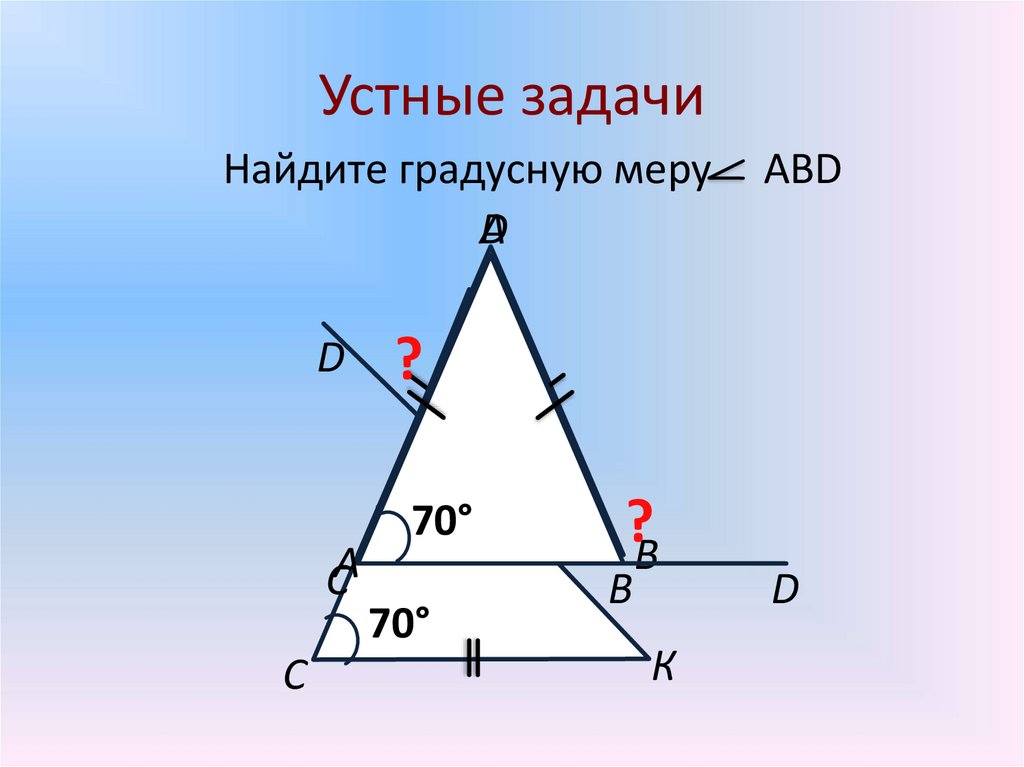
6. Устные задачи

Найдите градусную меру
D
А
А
D ?
В
СА
С
70°
70°
? ?
В
В
К
АВD
D

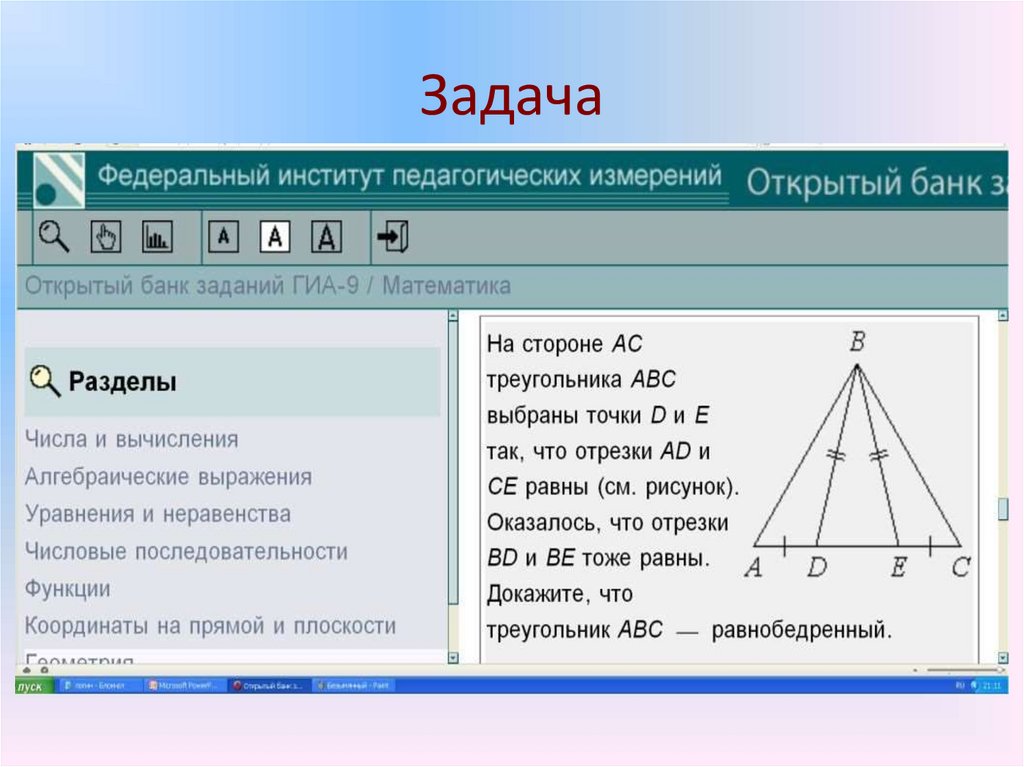
7. Задача

8.

Треугольников в мире не счесть
В жизни нам они часто встречаются
Среди них и особые есть
Равнобедренными называются.
Отличить от других их легко:
По бокам у них стороны равные
Есть у них ещё свойство одно:
Углы при основании равные.
Так же в них и биссектриса
Обладает отличительной чертой
К основанию проведенная,
Является медианой и высотой.
Будем свойства эти знать
Сдадим экзамены на «пять».

9. Домашнее задание

• п.18 (теорема 1 и её доказательство) стр.35;
№ 112; 116 стр. 37 – 38.
• В электронном дневнике

10. Интернет-ресурсы

• http://images.yandex.ru/
• http://fcior.edu.ru/card/4825/ravnobedrennyy
-treugolnik-i-ego-svoystva-perimetrravnobedrennogo-treugolnika-p2.html
• http://interneturok.ru/ru/school/geometry/7klass/treugolnikib/reshenie-zadach-po-temeravnobedrennyy-treugolnik
• http://www.fipi.ru/