Планиметрия. Аксиомы стереометрии

1. Планиметрия

А

2.

Стереометрия – это раздел
геометрии,в котором
изучаются фигуры в
пространстве.

3. Аксиомы стереометрии

Какова бы ни была
плоскость,существуют
точки,принадлежащие этой
плоскости, и точки,не
принадлежащие ей. С 1

4.

Если две различные
плоскости имеют общую
точку,то они пересекаются
по прямой,проходящей
через эту точку.С 2

5.

⍺
А
β

6.

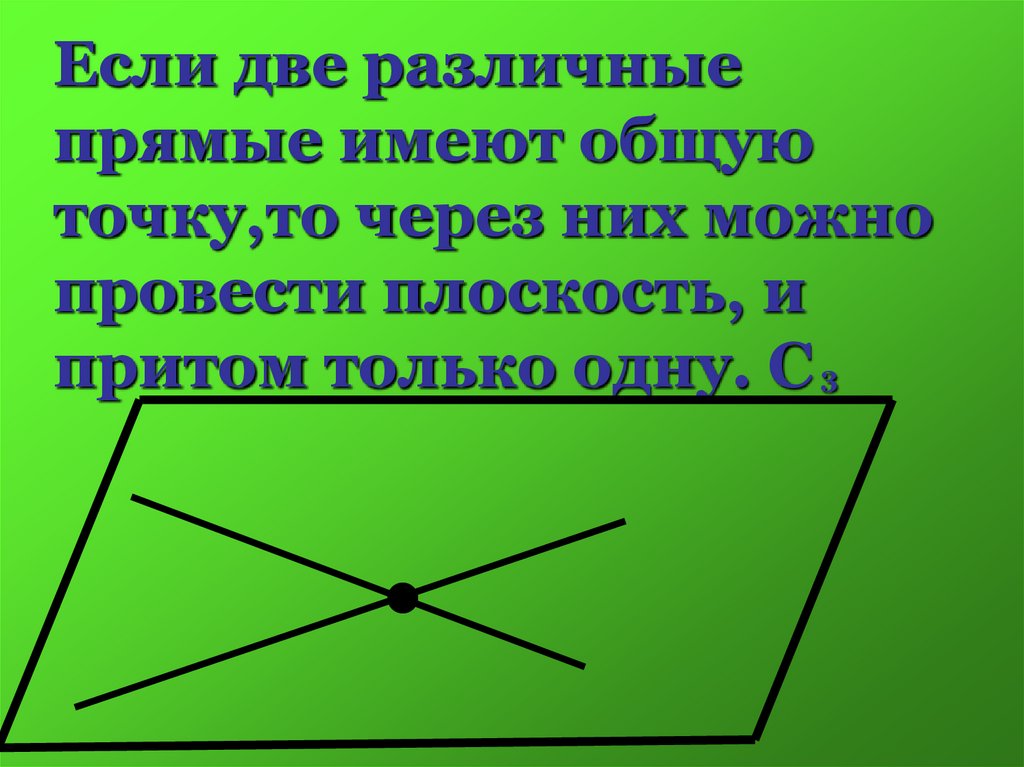
Если две различные
прямые имеют общую
точку,то через них можно
провести плоскость, и
притом только одну. С 3

7. Аксиомы планиметрии

1.Какова бы ни была прямая,существуют точки,принадлежащие этой прямой,и
точки,не принадлежащие ей.Через любые две точки можно провести прямую,и
только одну.
2.Из трех точек на прямой одна и только одна лежит между двумя другими.
3.Каждый отрезок имеет определенную длину,большую нуля.Длина отрезка
равна сумме длин частей,на которые он разбивается любой его точкой.
4.Прямая,принадлежащая плоскости,разбивает эту плоскость на две
полуплоскости.
5.Каждый угол имеет определенную градусную меру,большую
нуля.Развернутый угол равен 180.Градусная мера угла равна сумме градусных
мер углов,на которые он разбивается любым лучом,проходящим между его
сторонами.
6.На любой полупрямой от ее начальной точки можно отложить отрезок
заданной длины,и только один.
7.От полупрямой на содержащей ее плоскости в заданную полуплоскость
можно отложить угол с заданной градусной мерой,меньшей 180,и только один.
8.Каков бы ни был треугольник,существует равный ему треугольник в данной
плоскости в заданном расположении относительно данной полупрямой в этой
плоскости.
9.На плоскости через данную точку,не лежащую на данной прямой,можно
провести не более одной прямой,параллельной данной.

8.

Через прямую и не лежащую на ней
точку проходит плоскость, и притом
только одна.
а
P
Q
М
⍺

9.

Если две точки прямой лежат в
плоскости, то и прямая
лежит в плоскости.
В
А
⍺

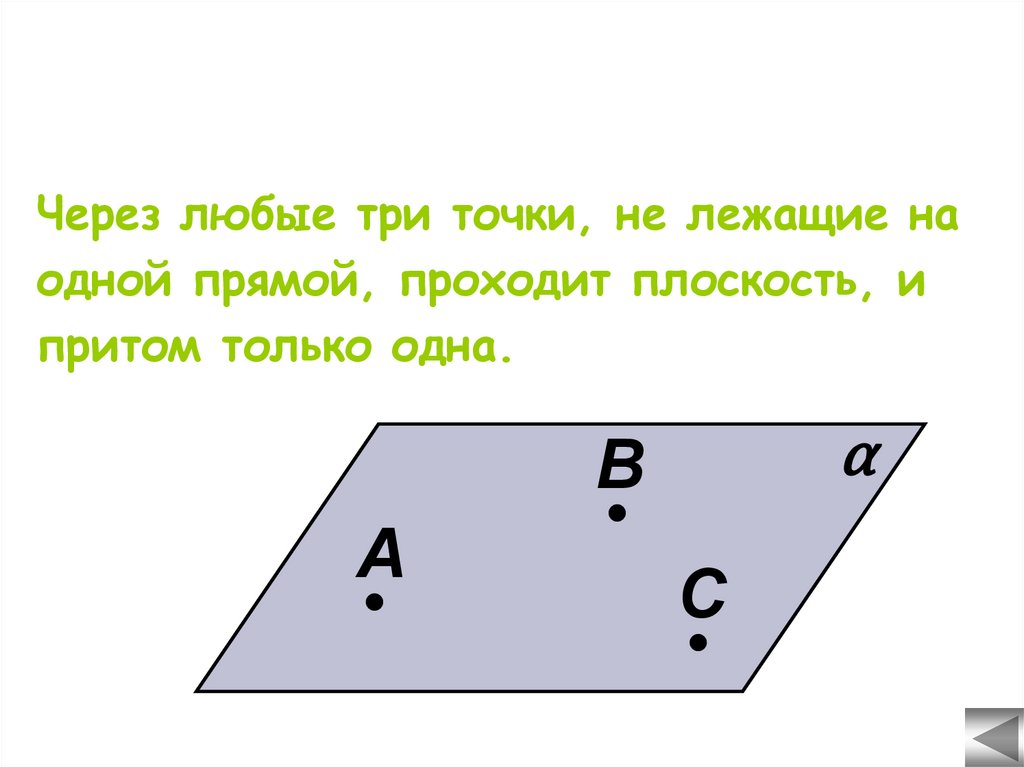
10.

Через любые три точки, не лежащие на
одной прямой, проходит плоскость, и
притом только одна.
⍺
В
А
С

11.

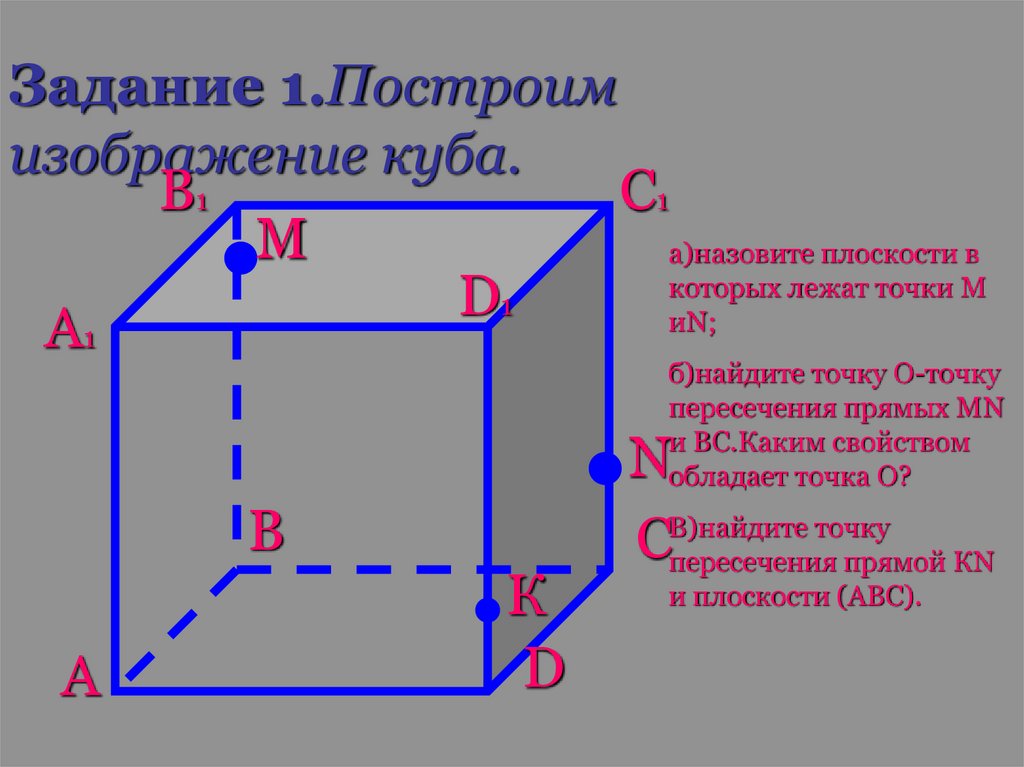
Задание 1.Построим
изображение куба.
В1
С1
М
а)назовите плоскости в
которых лежат точки М
D1
иN;
А1
б)найдите точку О-точку
пересечения прямых МN
и ВС.Каким свойством
обладает точка О?
В
А
К
D
N
точку
СВ)найдите
пересечения прямой КN
и плоскости (АВС).

12.

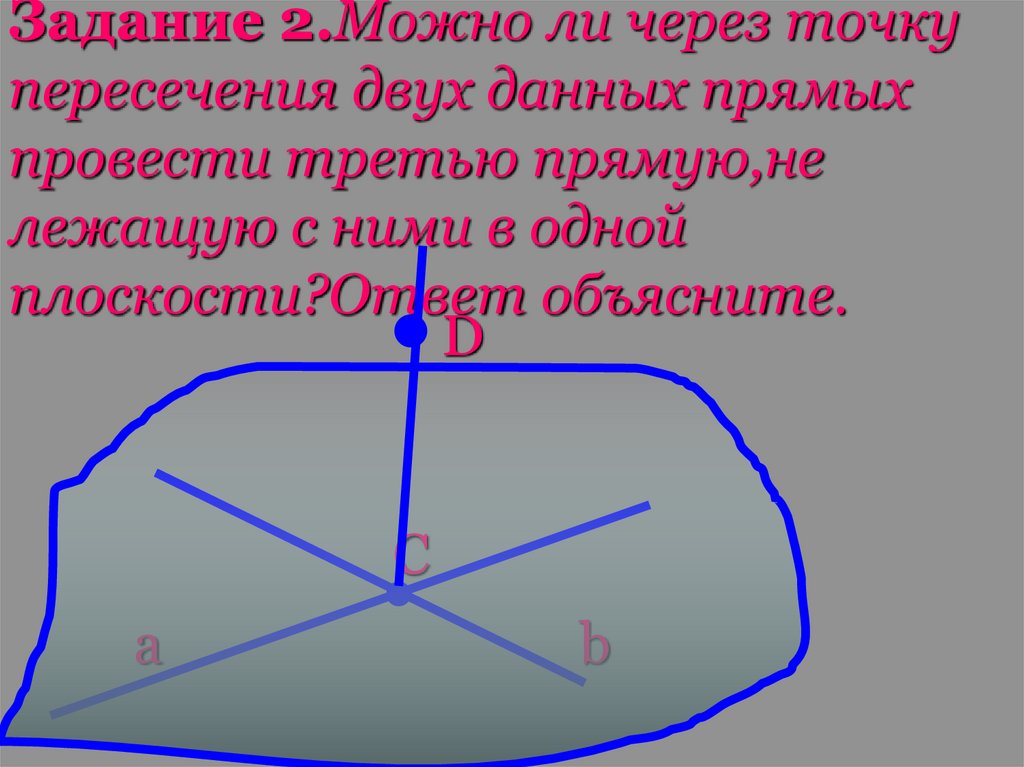
Задание 2.Можно ли через точку
пересечения двух данных прямых
провести третью прямую,не
лежащую с ними в одной
плоскости?Ответ объясните.
D
C
а
b

13.

Устная работа
Найдите ошибку.Ответ обоснуйте
D
М
О
N
С
А
В
МNпересекает ВD в
точке О

14.

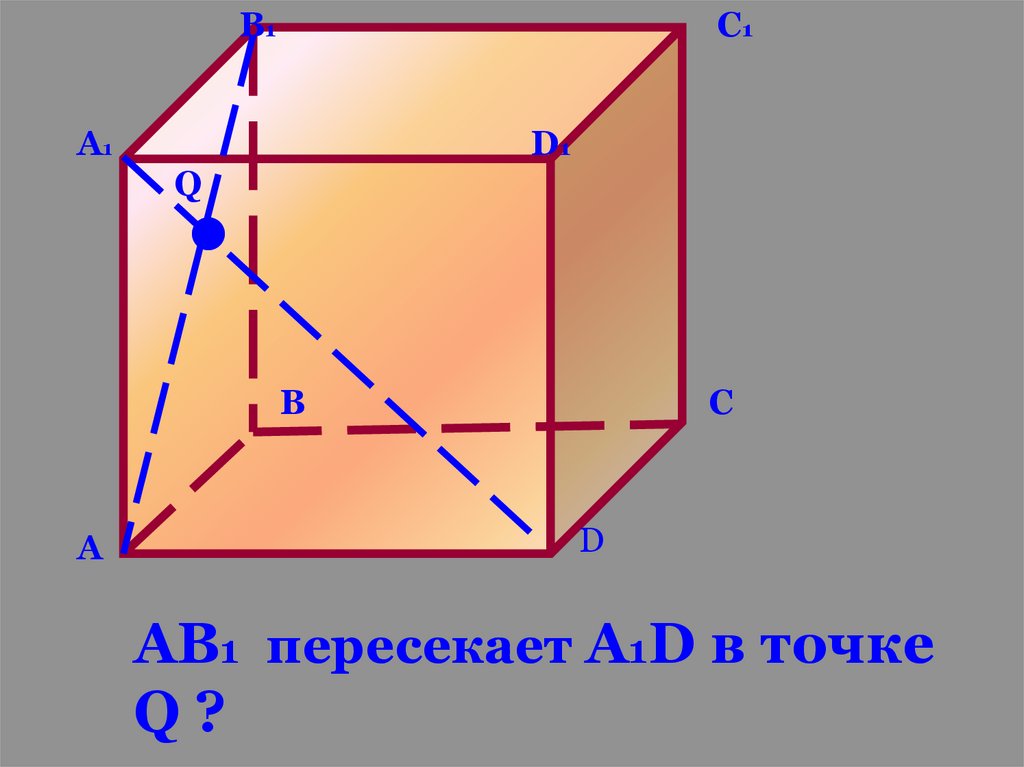
В1
С1
А1
D1
Q
В
А
С
D
АВ1 пересекает А1D в точке
Q?

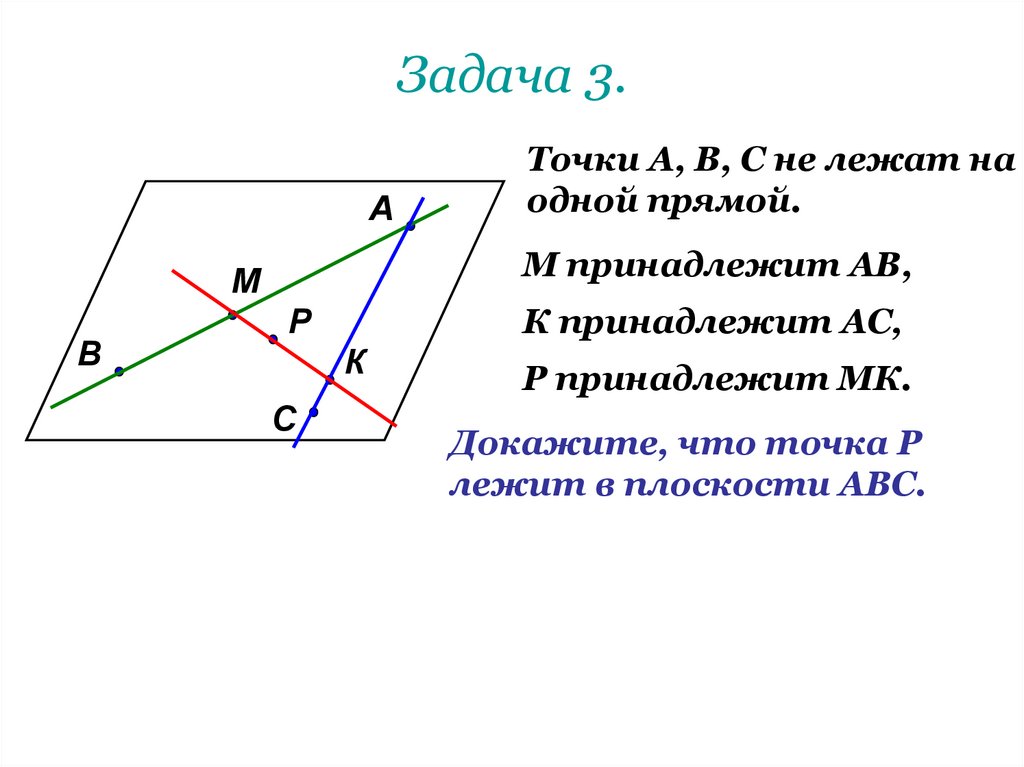
15. Задача 3.

А
М принадлежит АВ,
М
В
Точки А, В, С не лежат на
одной прямой.
К принадлежит АС,
Р
К
С
Р принадлежит МК.
Докажите, что точка Р
лежит в плоскости АВС.

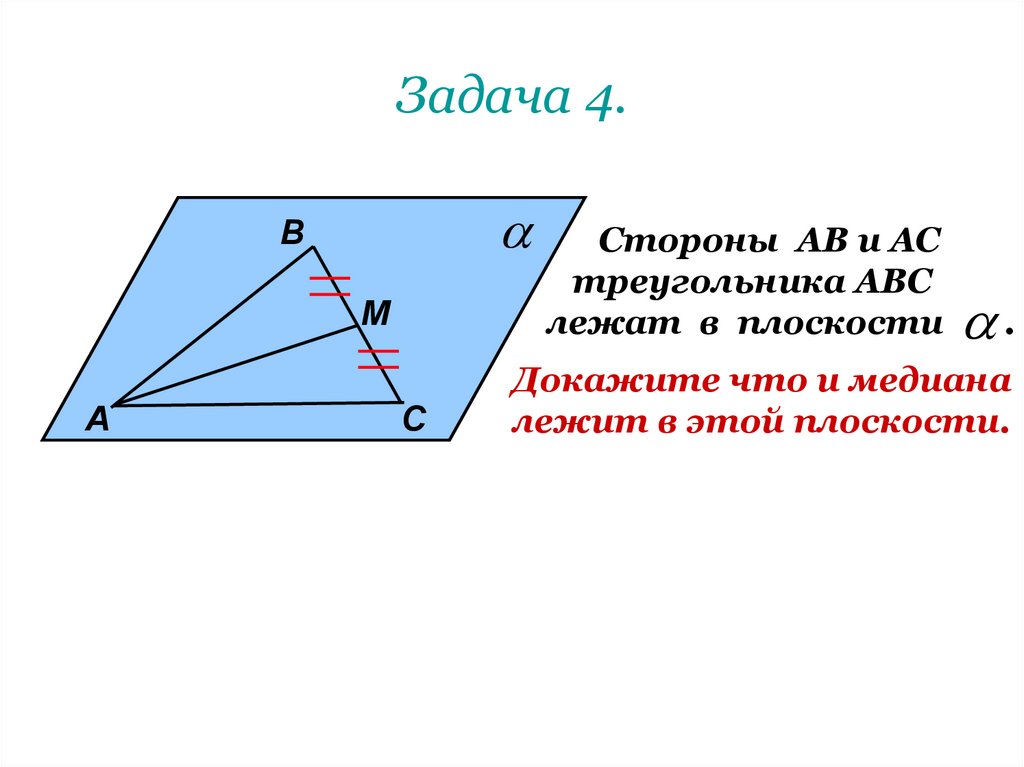
16. Задача 4.

В
М
А
С
Стороны АВ и АС
треугольника АВС
лежат в плоскости
.
Докажите что и медиана
лежит в этой плоскости.

17.

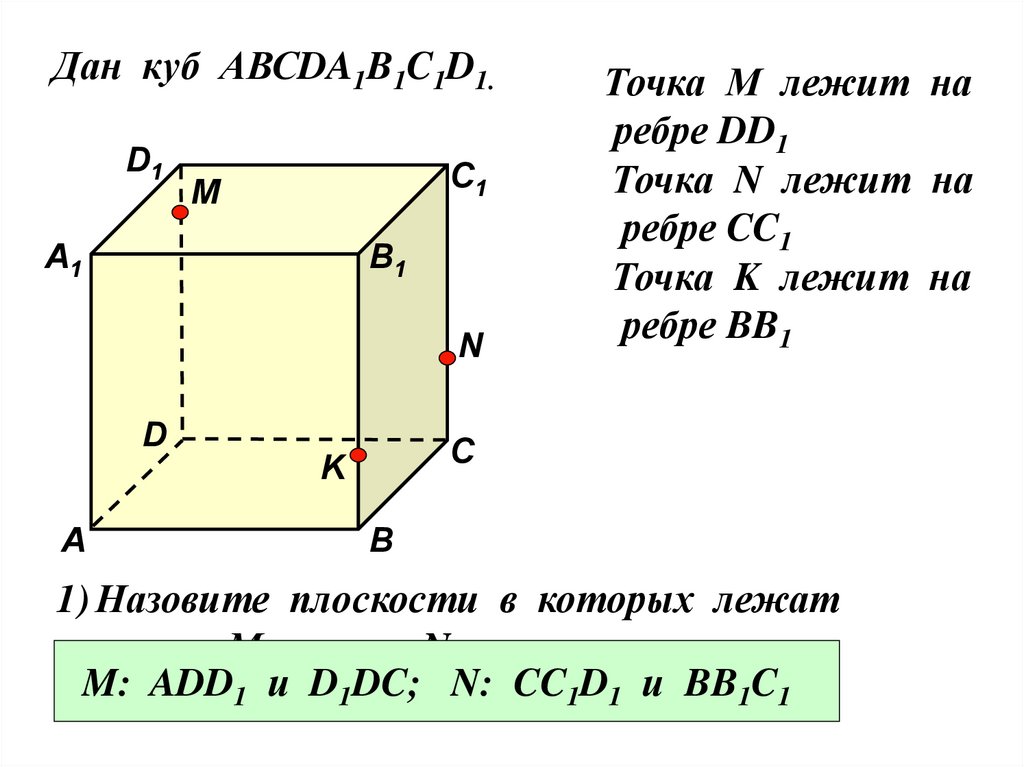
Дан куб АВСDA1B1C1D1.
D1
С1
M
А1
В1
N
D
С
K
А
Точка М лежит на
ребре DD1
Точка N лежит на
ребре CC1
Точка K лежит на
ребре BB1
В
1) Назовите плоскости в которых лежат
точка М, точка N.
M: ADD1 и D1DC; N: CC1D1 и BB1C1

18.

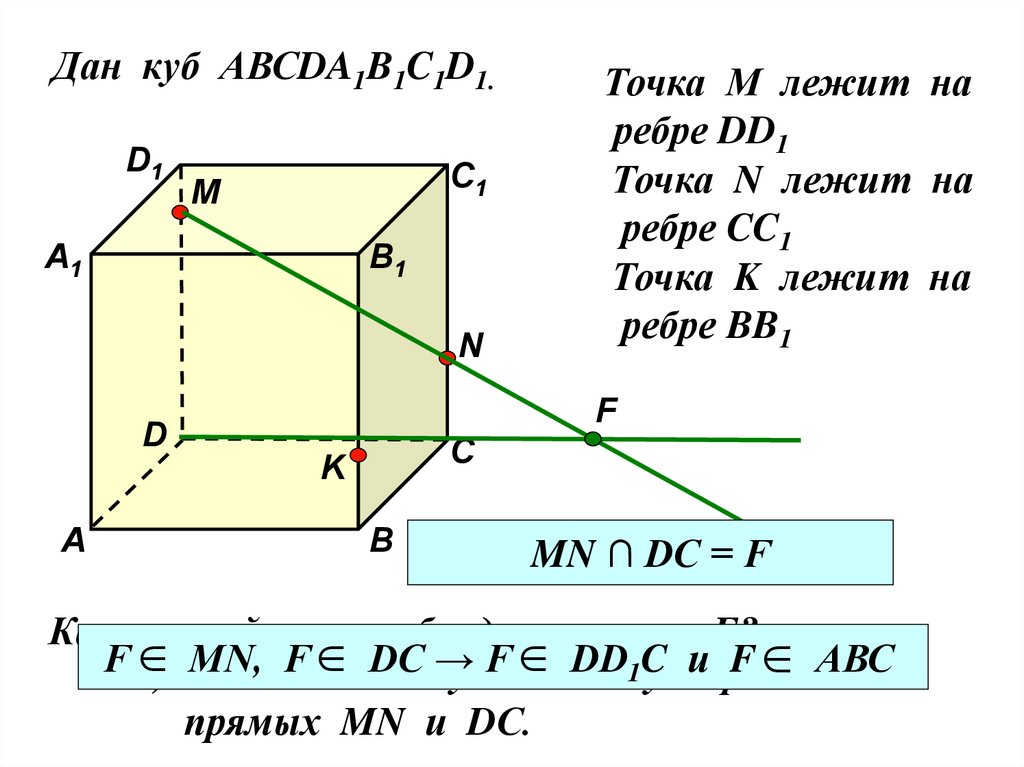
Дан куб АВСDA1B1C1D1.
D1
С1
M
А1
В1
N
F
D
С
K
А
Точка М лежит на
ребре DD1
Точка N лежит на
ребре CC1
Точка K лежит на
ребре BB1
В
MN ∩ DC = F
Каким свойством обладает точка F?
F
MN, F точку
DC → F
DD1C пересечения
и F АВС
2) Найдите
F
– точку
прямых MN и DС.

19.

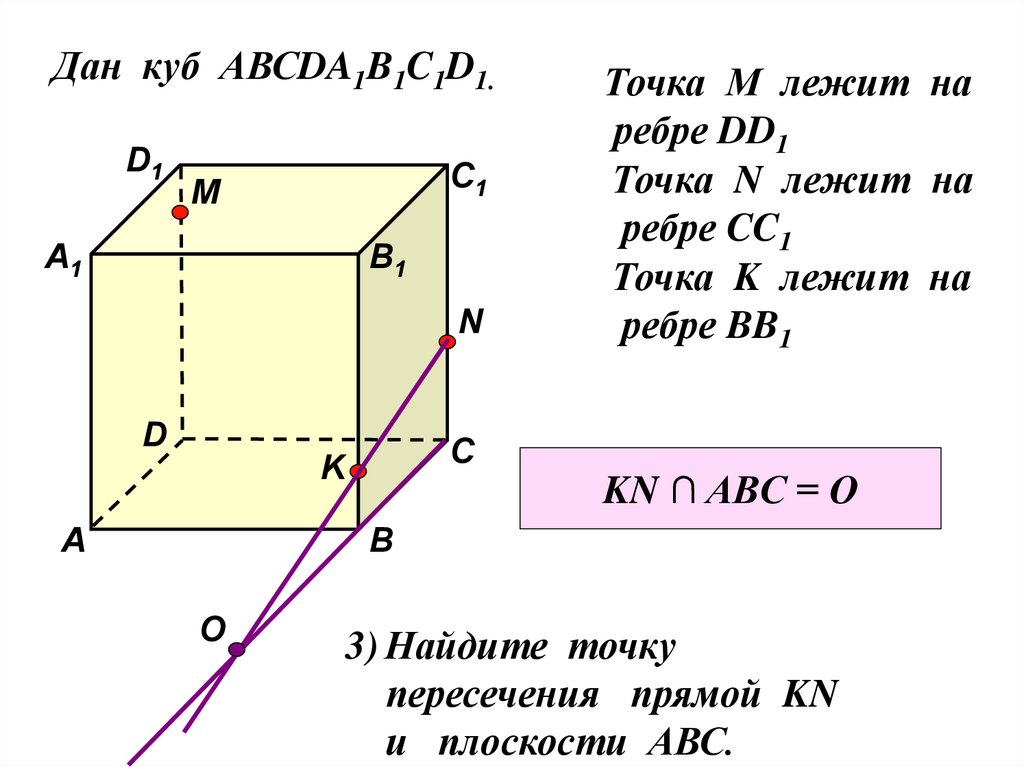
Дан куб АВСDA1B1C1D1.
D1
С1
M
А1
В1
N
D
С
K
А
Точка М лежит на
ребре DD1
Точка N лежит на
ребре CC1
Точка K лежит на
ребре BB1
KN ∩ ABC = O
В
О
3) Найдите точку
пересечения прямой KN
и плоскости АВС.

20.

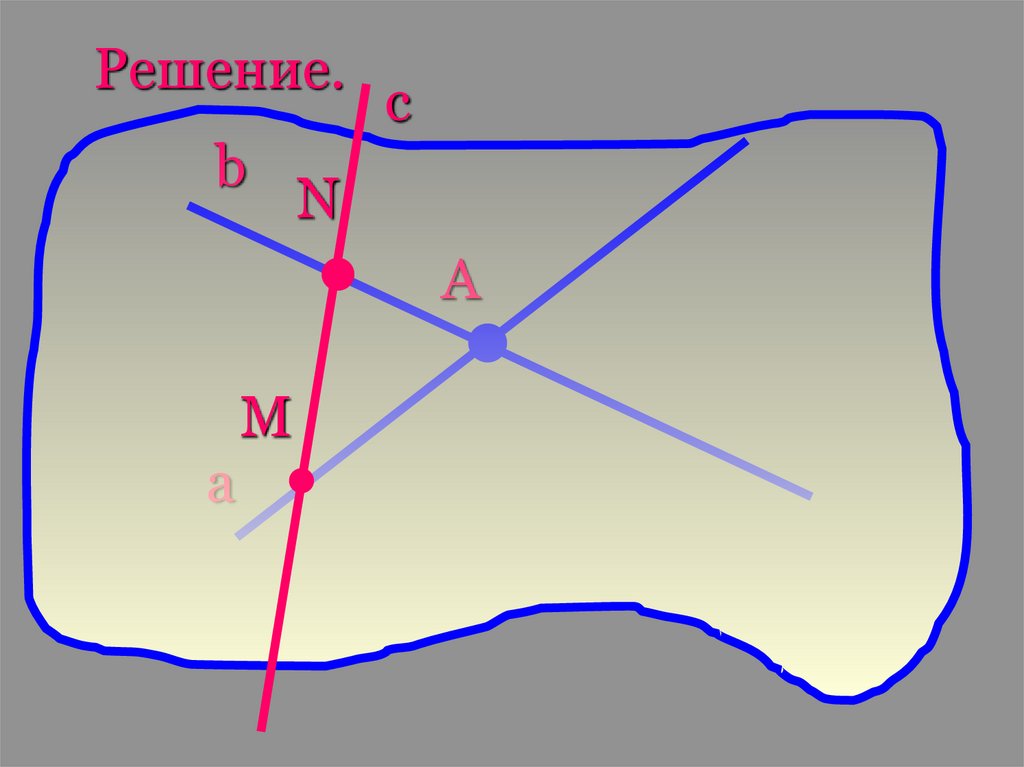
Задача.Даны две различные
прямые,пересекающиеся в точке
А.Докажите,что все
прямые,пересекающие обе данные
прямые и не проходящие через
точку А,лежат в одной плоскости.

21.

Решение.
b
с
N
А
М
а