Изучение микроструктуры процессов релаксации в плазме

1. Дипломная работа

тема: «Изучение микроструктуры
процессов релаксации в плазме»
Выполнила студентка 6 курса Переславцева МГ

2.

Исследование
процессов
релаксации в
плазме является
одной из наиболее
актуальных задач
современной
физики.

3. Я рассмотрела одну из моделей, описываемую уравнением

LU (t , r ) = f (r , t ), r = {x, y , z} Î R 3 , t > 0
(1)
где:
¶3
¶2
¶
¶
¶3
¶2
¶
¶2 ¶2
L º (a3 3 - a2 2 + a1 + a0 )( + b3 3 - b2 2 + b1 + b0 ) - 2 - 2
¶x
¶x
¶x
¶t
¶x
¶x
¶x
¶y ¶z
ak , bk ³ 0; a3 + b3 > 0
(2)

4.

U (r , t ) = (r , t ) (r , t )
(3)

5. a={0,0,0,1} и b={0,0,1,0} уравнения (1) с оператором:

¶
¶
¶
¶
Lº
- 5 + 2 + 2.
3
¶t ¶x ¶x ¶y ¶z
4
5
2
2
(4)

6. Задача Коши, для которой построено Засориным Ю.В. ФРК:

r
ì LE (r , t ) = 0, r = ( x, y, z ), t > 0;
ï 3
r
r
ï¶ E
3
=
d
(
r
),
r
Î
R
;
í 3 t =+0
ï ¶x r
r
ï E (t , r ) = o (1), r ® +¥.
î
(5)
d(r) – трехмерная дельта-функция Дирака, для которой
выполняется:
ò
R3
r
r r r
3
f (r )d (r )dr = f (0), "f Î C ( R ),

7. Фундаментальное решение:

c
r
E (t , r ) = 2 2 exp(w1 ) Ai(w2 ),
r 3t 3
4 (8t 3 + 9r 2 x)t 2
w1 =
,
4
27
r
2
3
2
3
1 (3r 2 x + 4t 3 )3 2
w2 =
,
2 1
9
2 r
r ( )3
t
r 2 = y2 + z2 ,
r
r = ( x, y, z ).
(6)

8.

9. Расчет параметров W1 и W2

10. Цель работы:

Построение поверхностей уровня
G c = {r Î R : E (r , t ) = C}
3
(7)
В различные моменты времени t>0 при
различных значениях С
В рамках данной работы рассмотрены
четыре момента времени(t=0.1, t=0.3, t=1,
t=2), для каждого из них был подобран
масштаб, построены линии уровня.

11. Построение поверхностей уровня для E=0

E0 ( x, r , t ) º
C
2 2
3 3
exp(w1 ) Ai (w2 ) , отсюда следует
r t
1 -1
3 3
2
3
3
3
4t
xn = ( ) t (r ) zn - 2
4
3r
3 ü
ì 3
zn = - í( )p ( n + ) ý
4 þ
î 2
2
3
-нули функции Эйри

12. Фрагмент программы для t=0.1

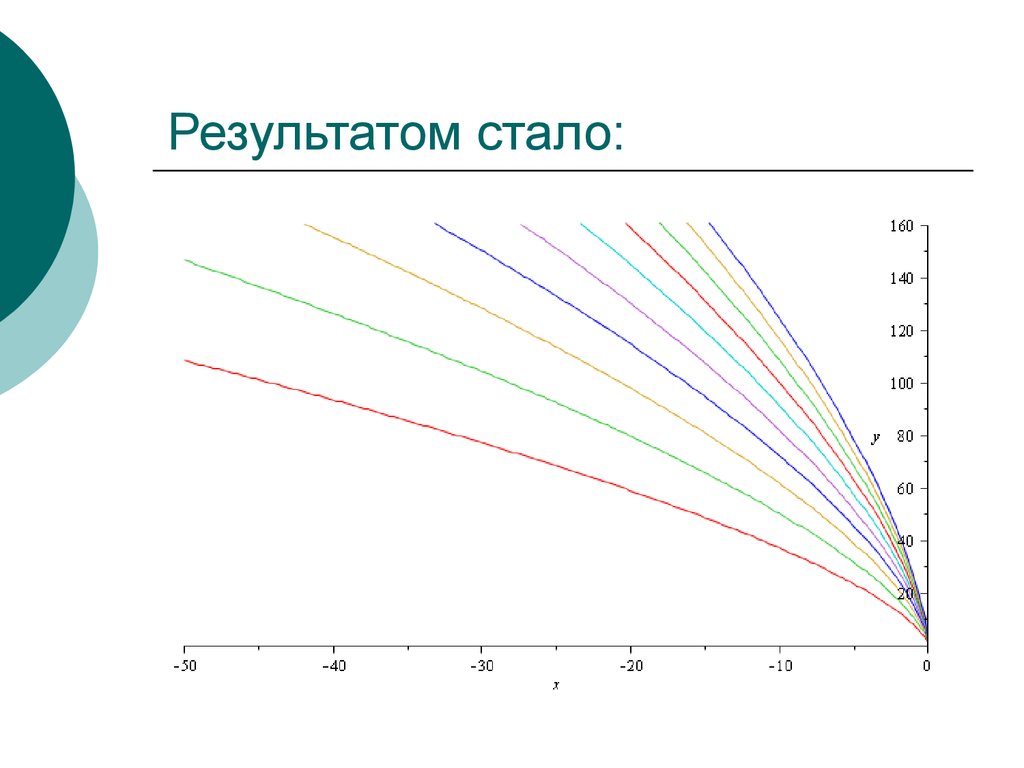
13. Результатом стало:

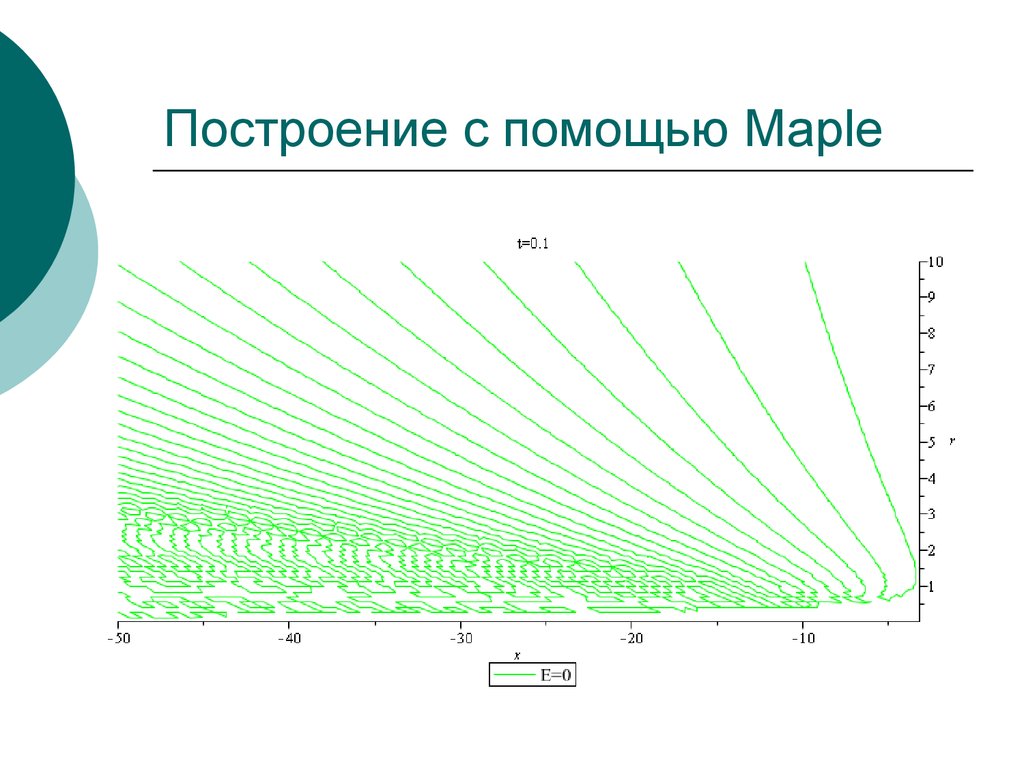
14. Построение с помощью Maple

15. Пример построения графика

16.

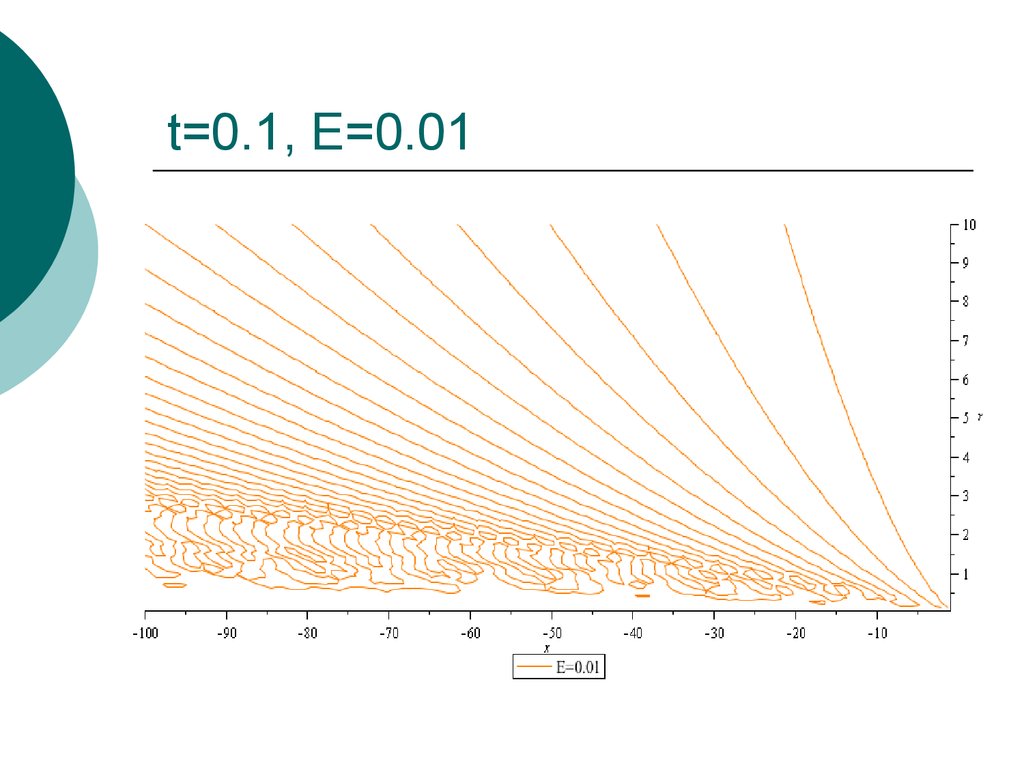
17. t=0.1, E=0.01

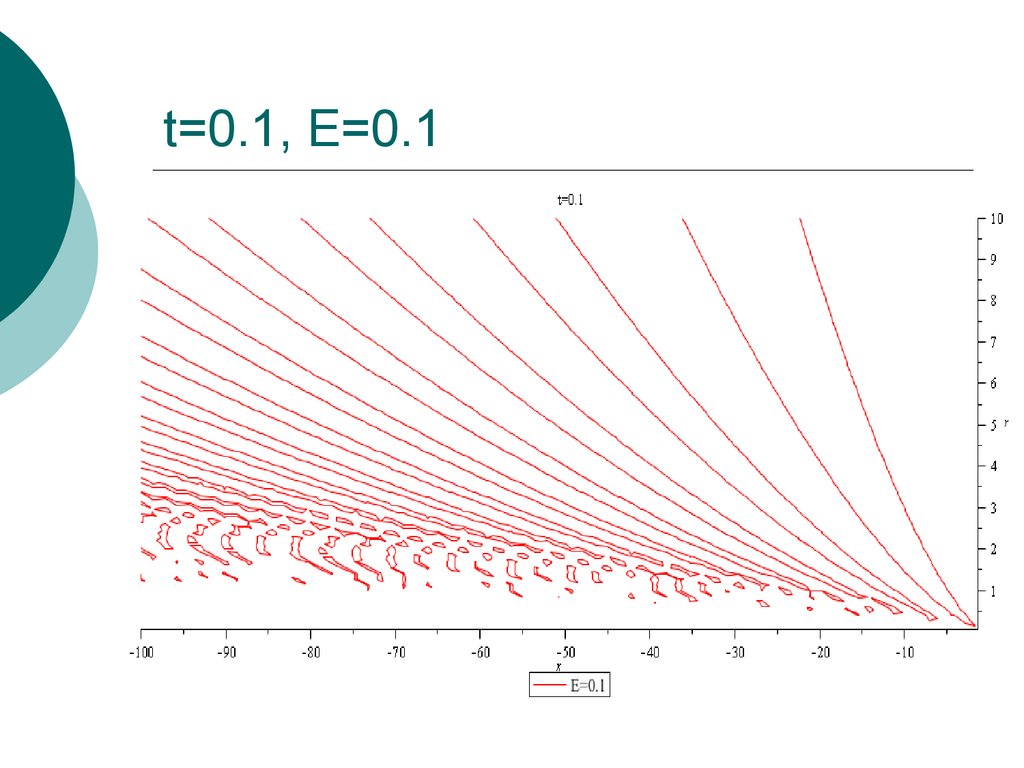
18. t=0.1, E=0.1

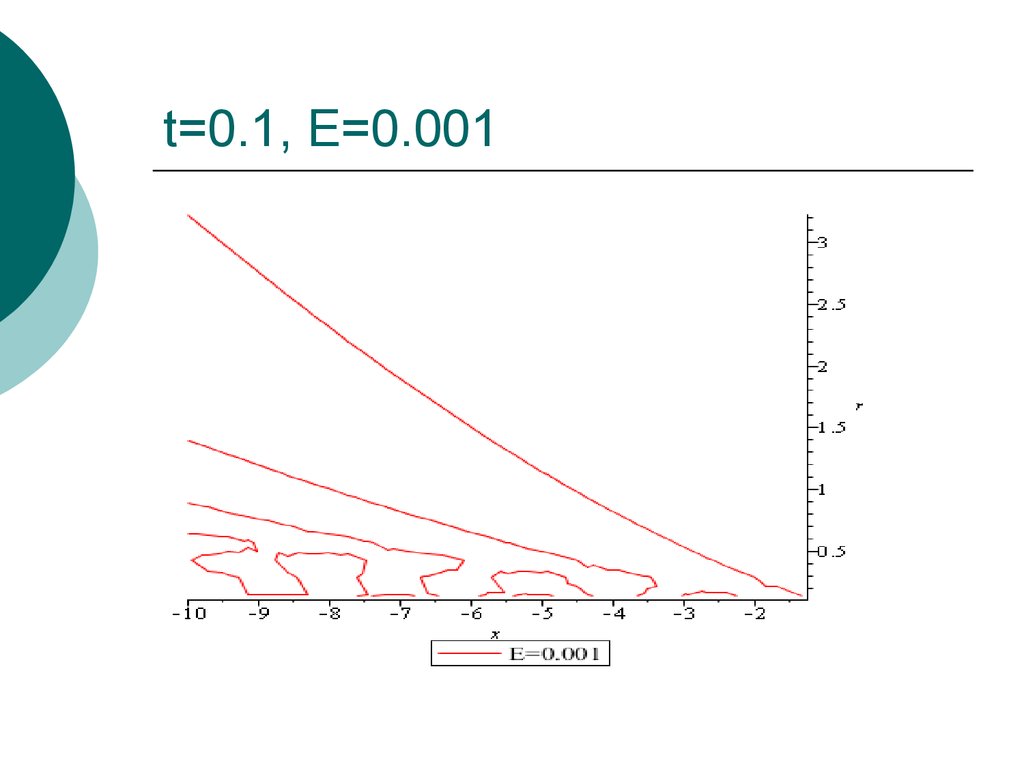
19. t=0.1, E=0.001

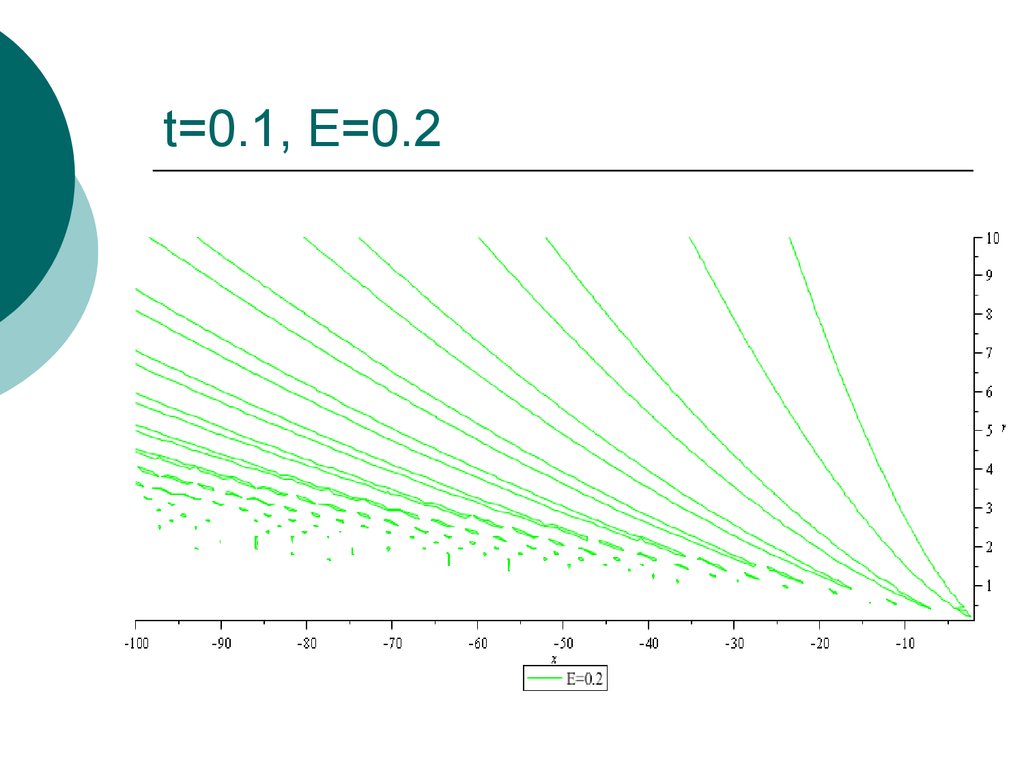
20. t=0.1, E=0.2

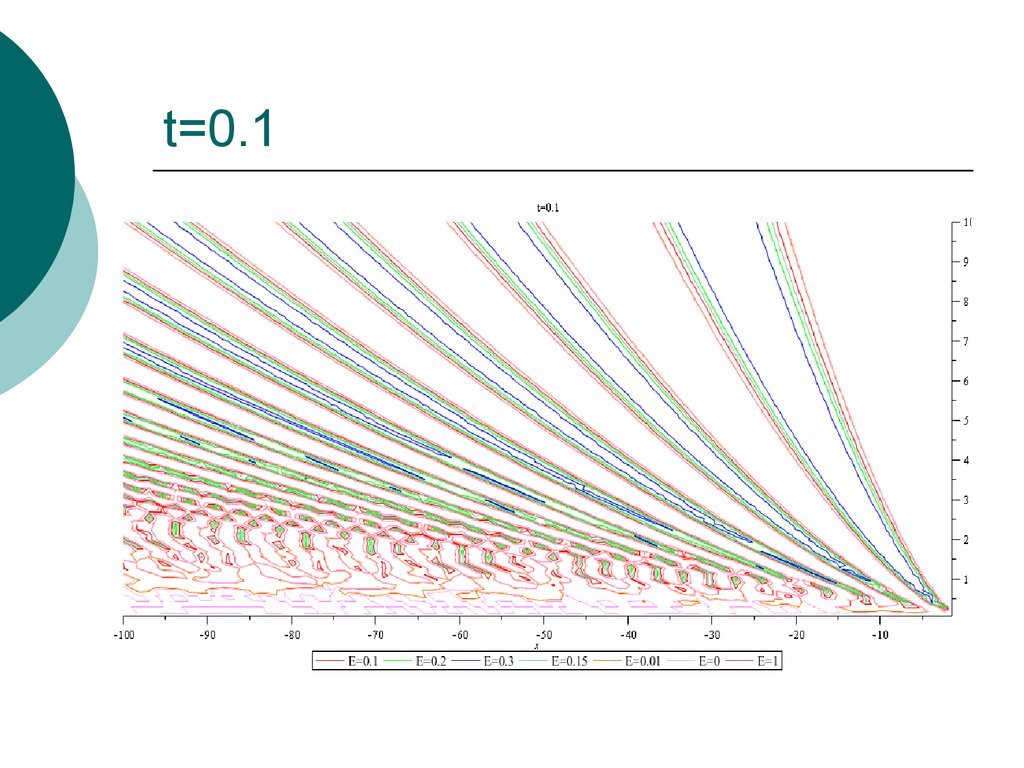
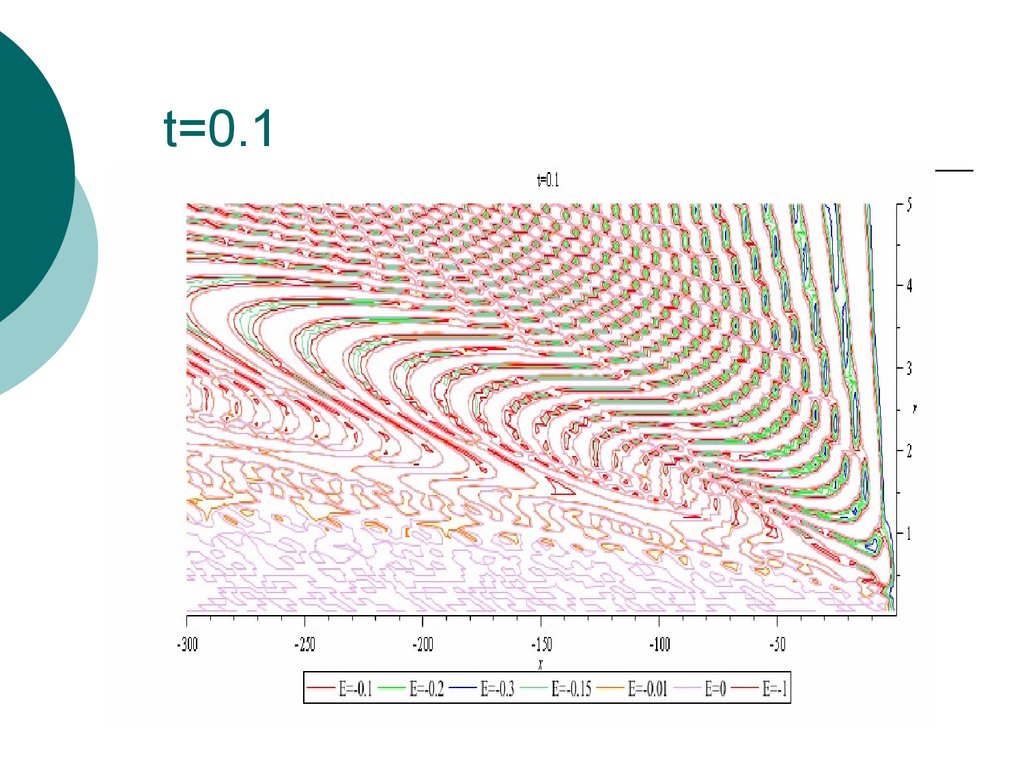
21. t=0.1

22. t=0.1

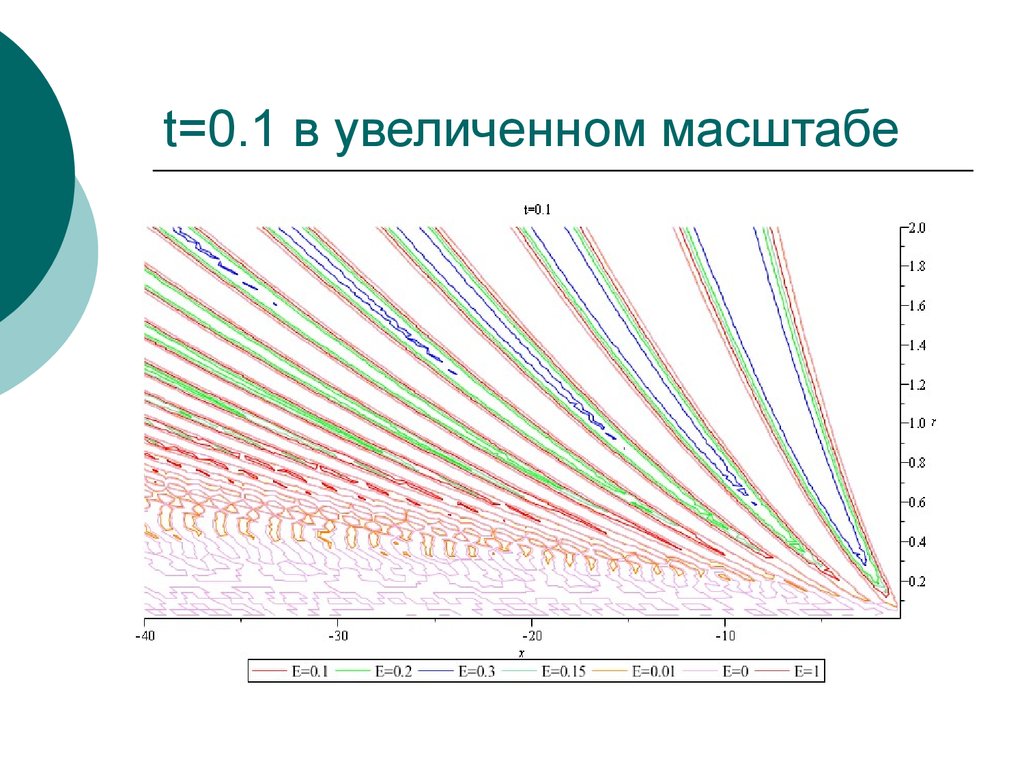
23. t=0.1 в увеличенном масштабе

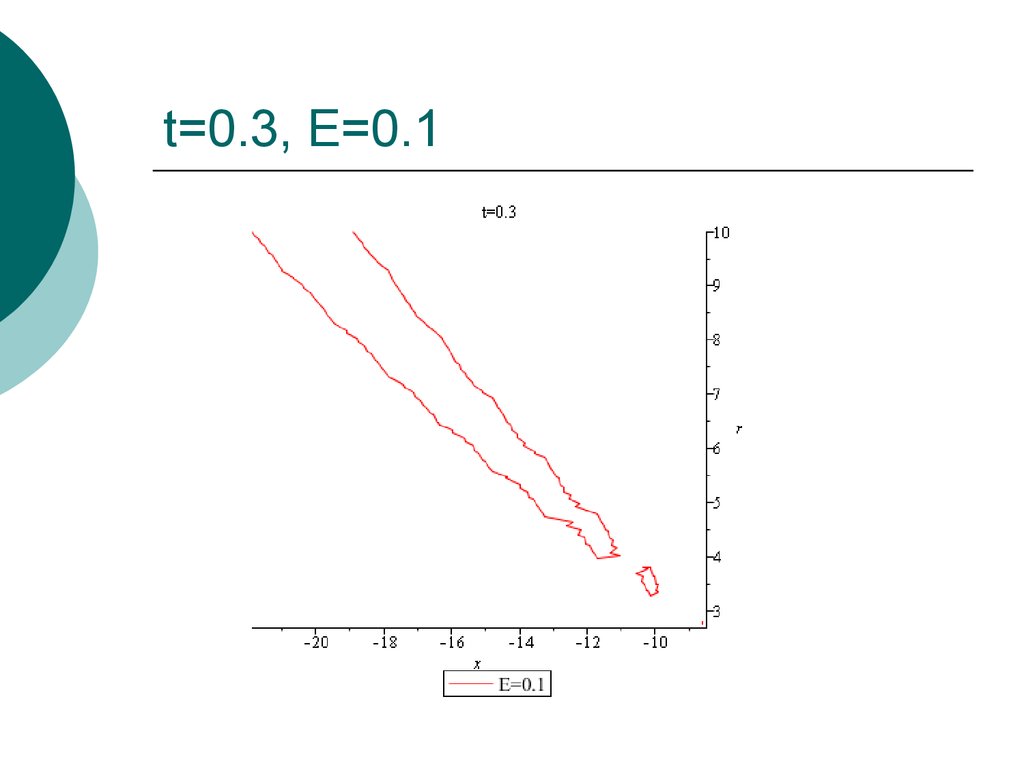
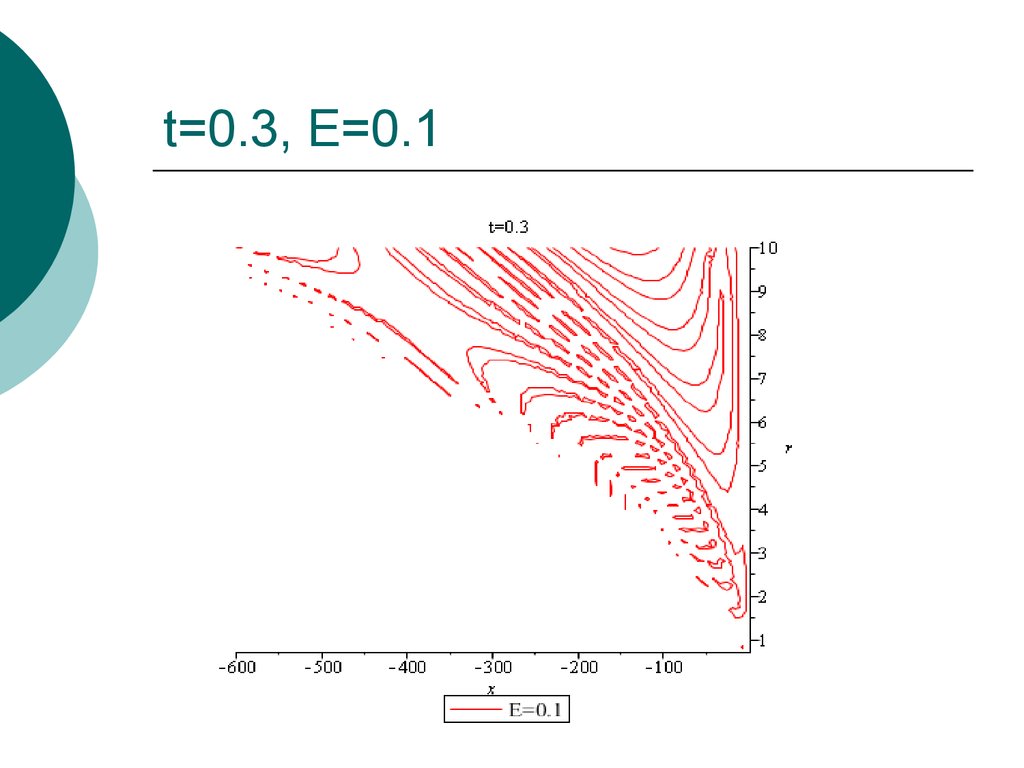
24. t=0.3, E=0.1

25. t=0.3, E=0.1

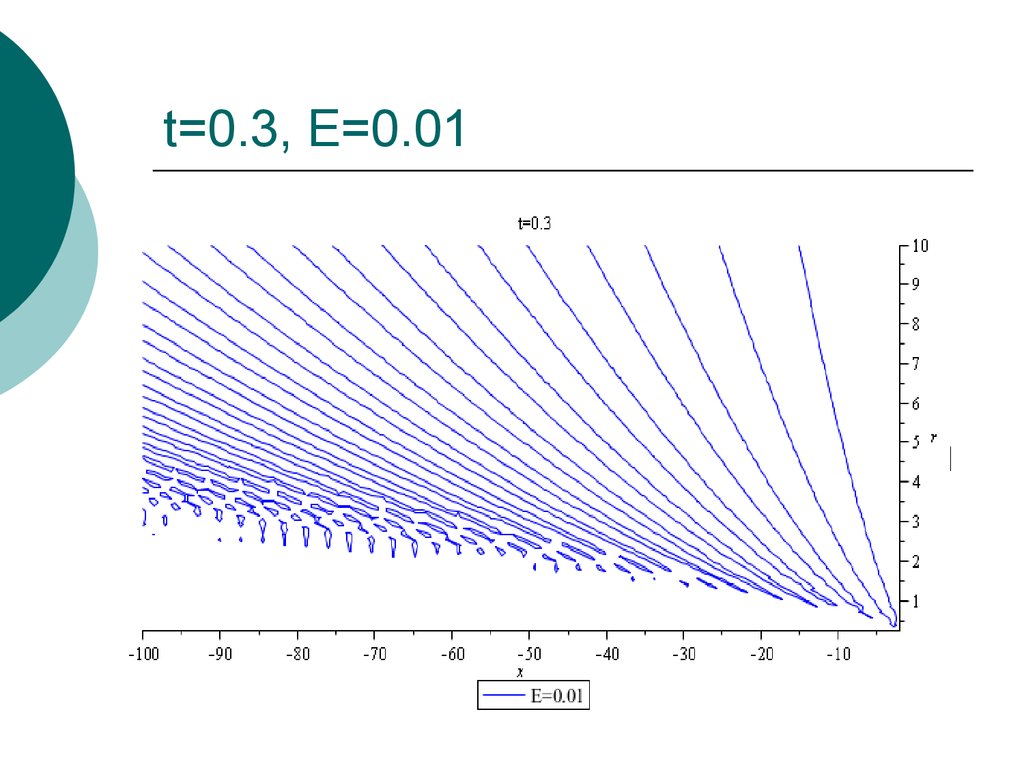
26. t=0.3, E=0.01

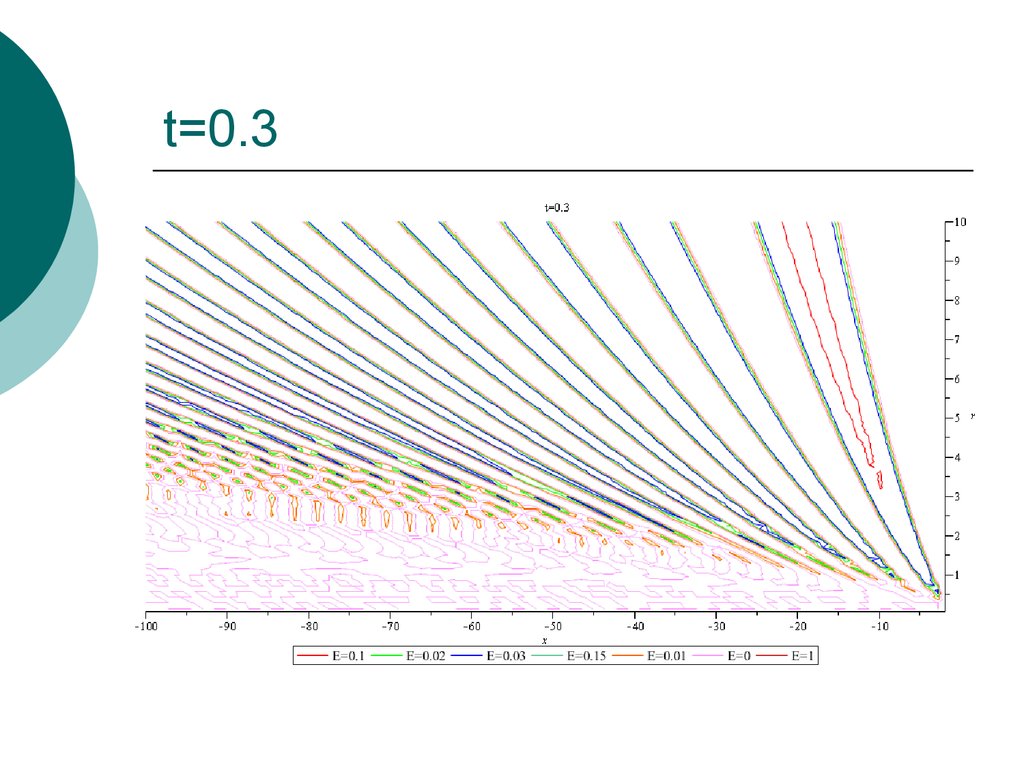
27. t=0.3

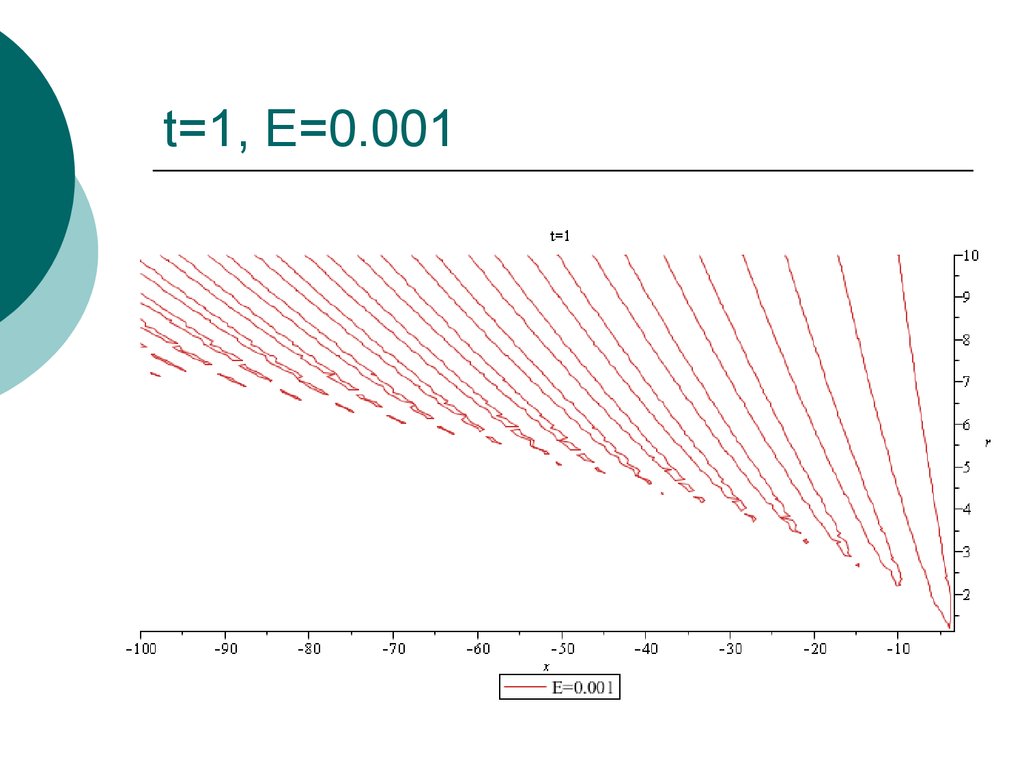
28. t=1, E=0.001

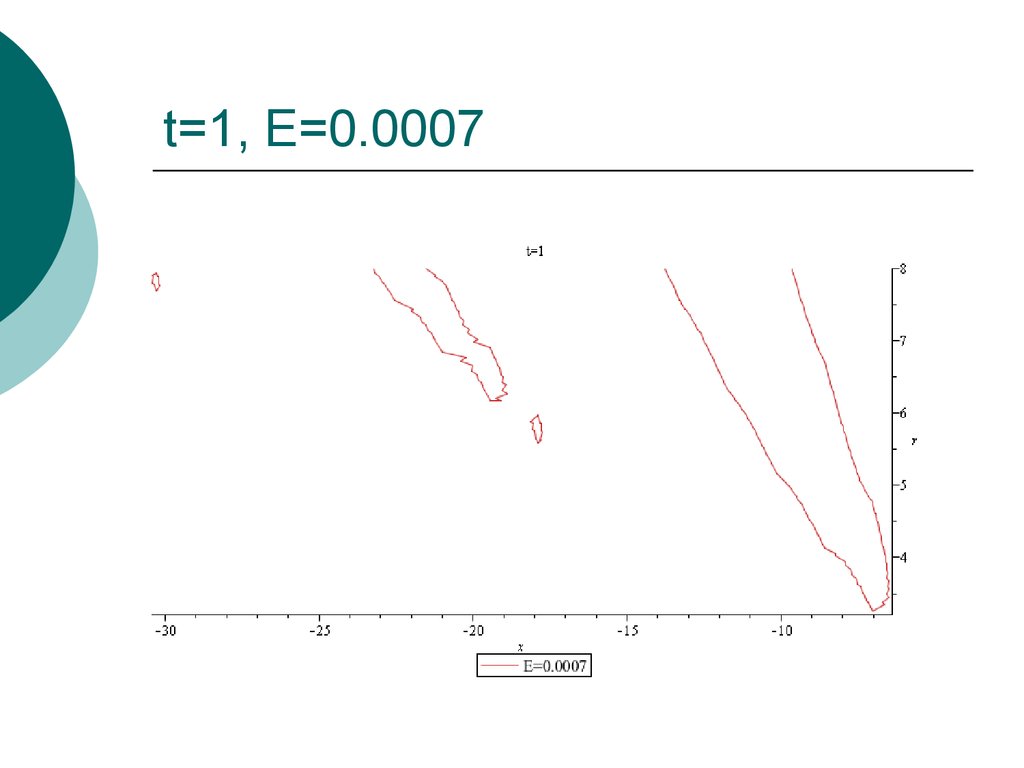
29. t=1, E=0.0007

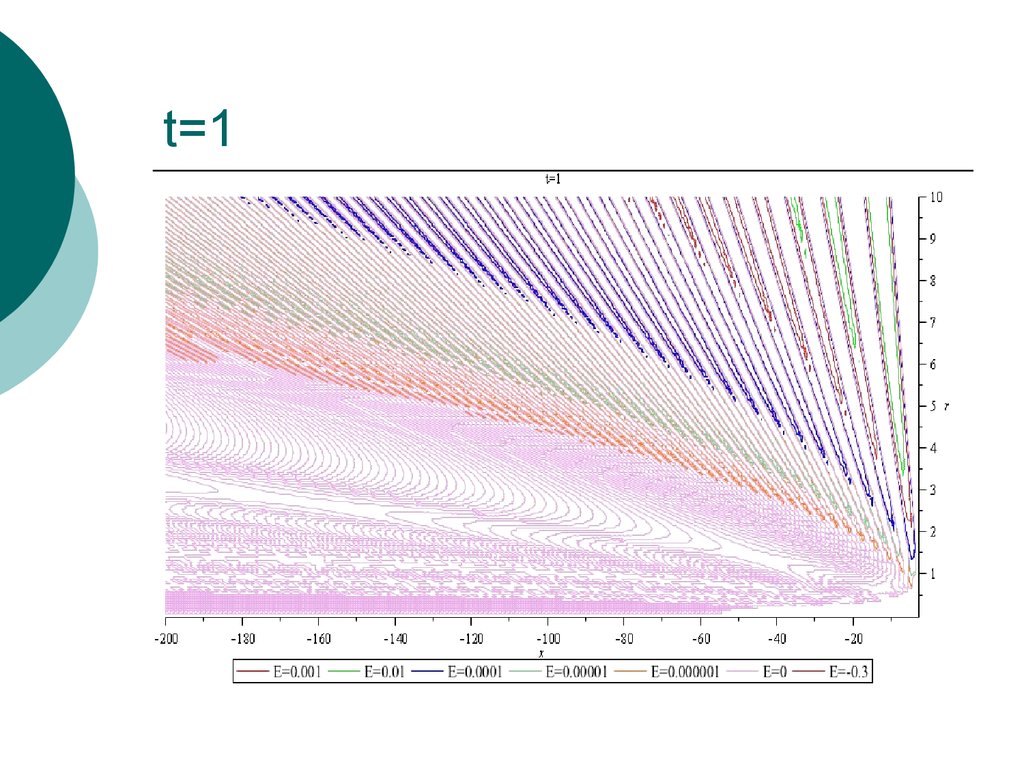
30. t=1

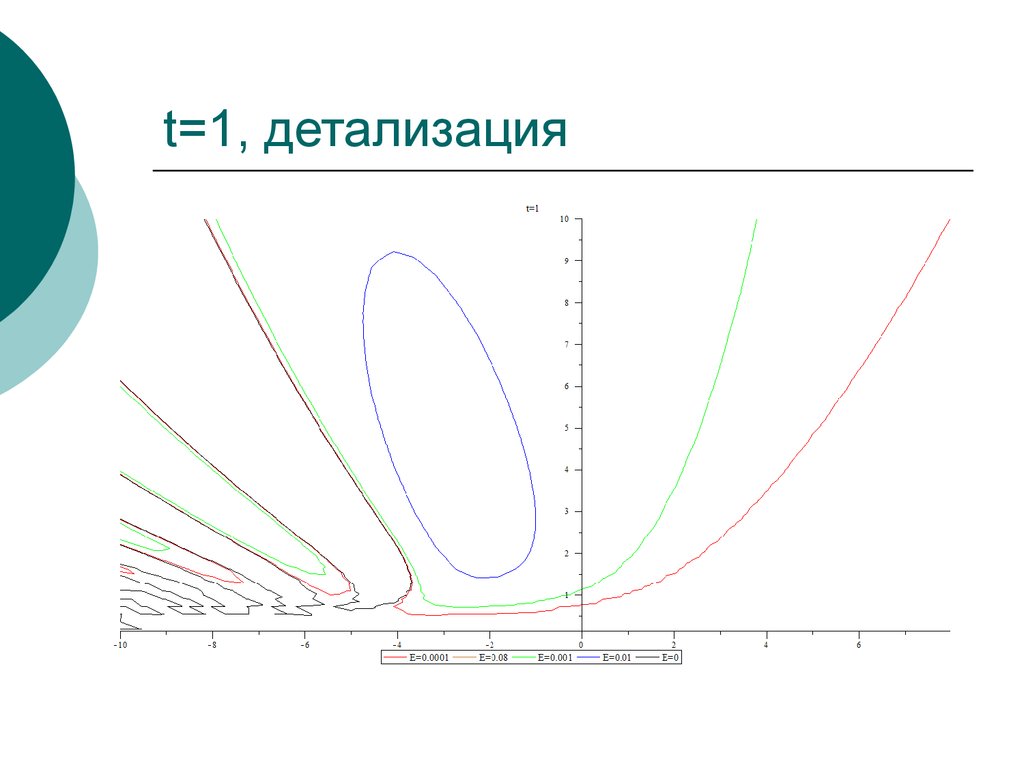
31. t=1, детализация

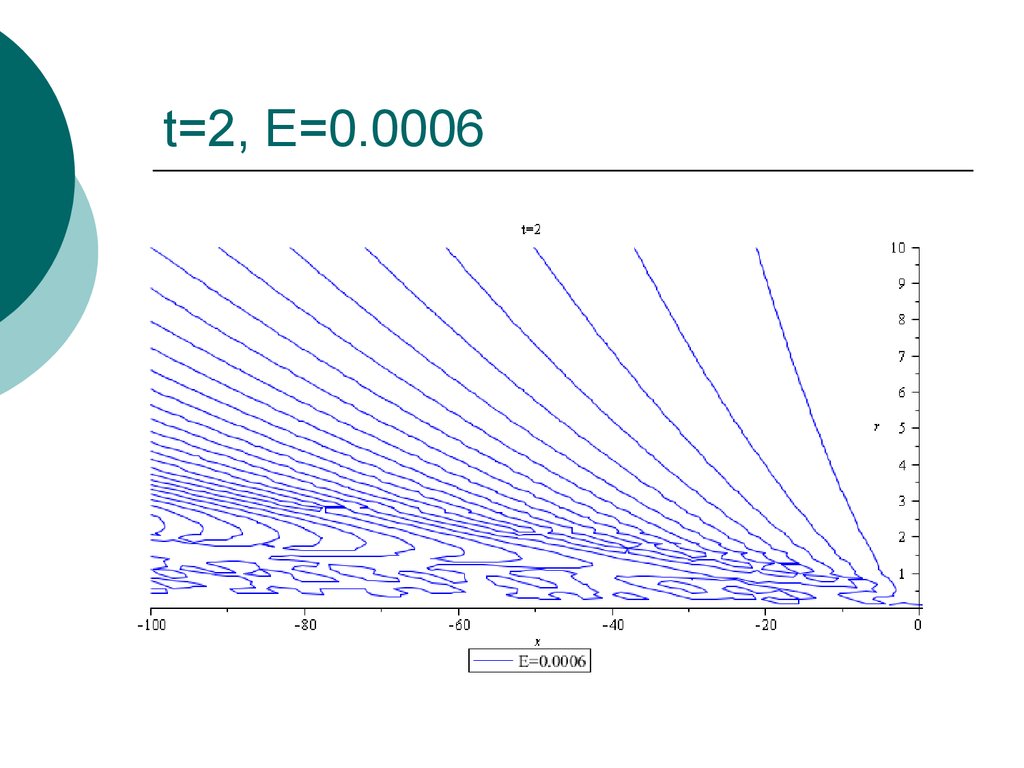
32. t=2, E=0.0006

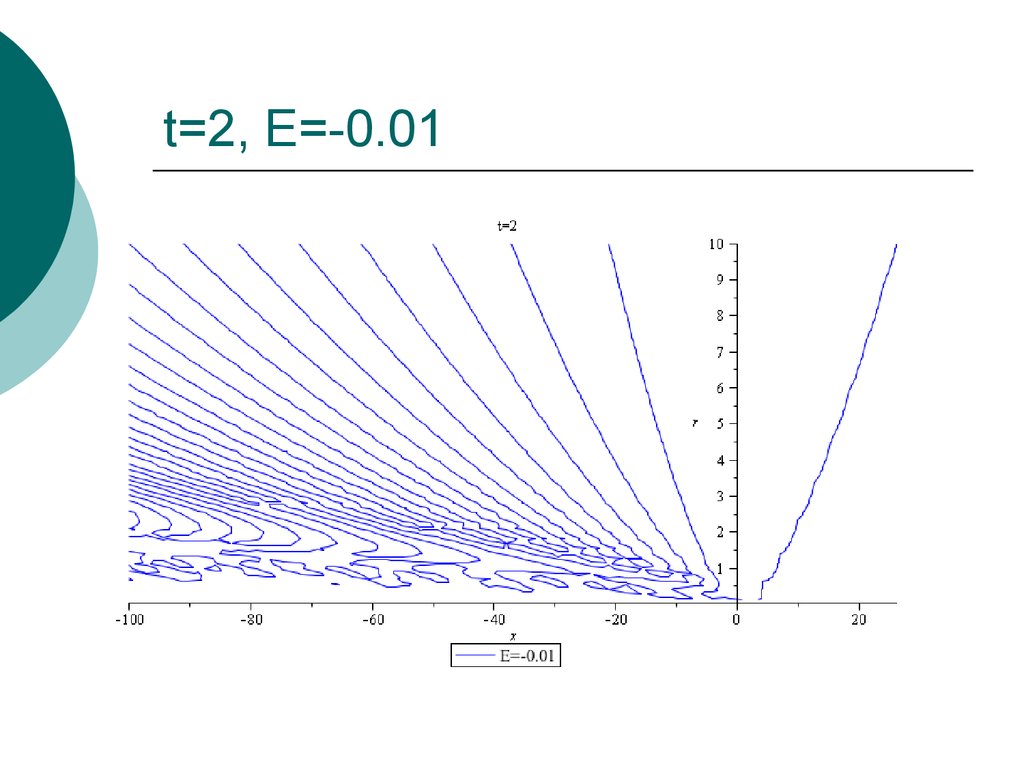
33. t=2, E=-0.01

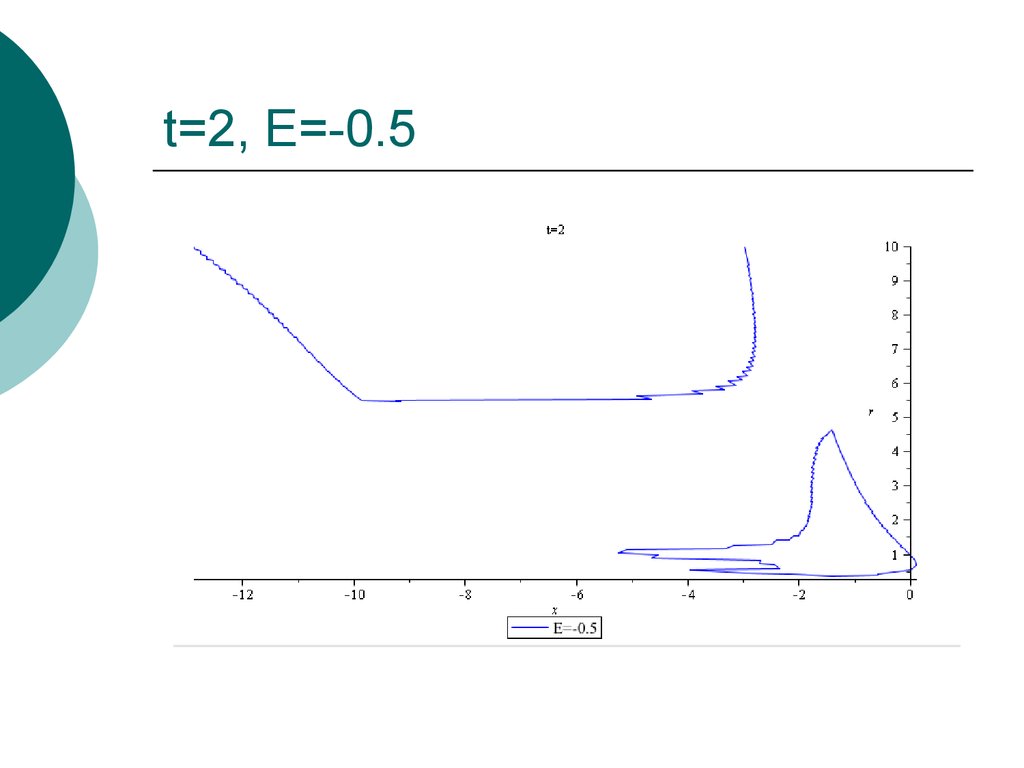
34. t=2, E=-0.5

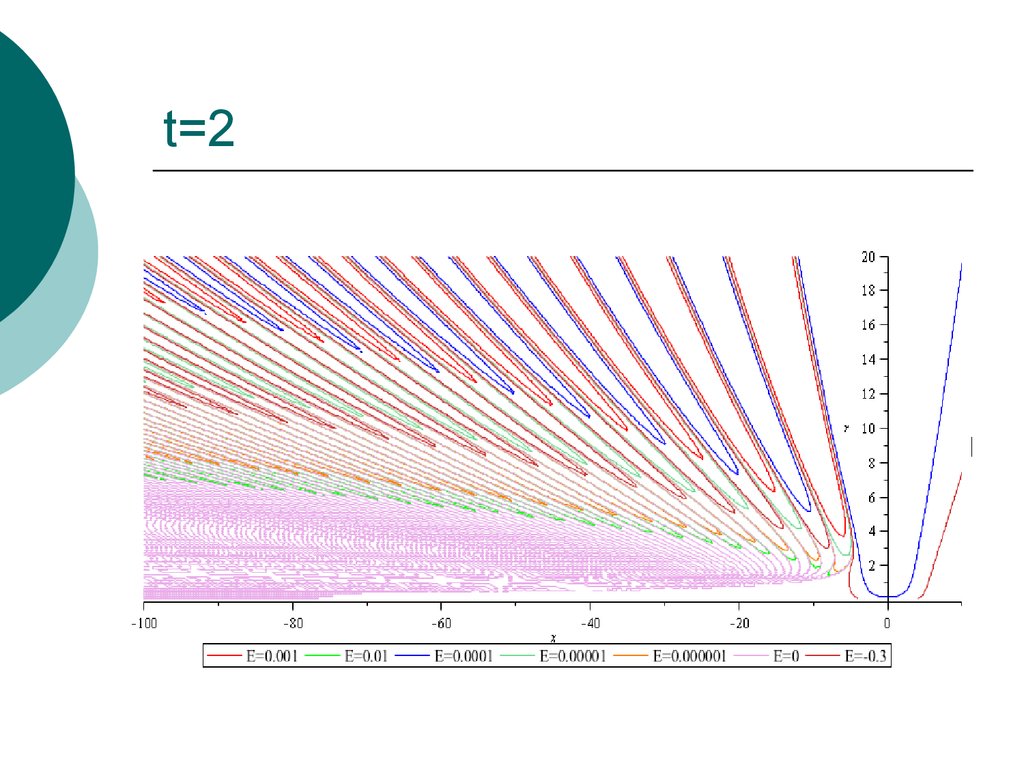
35. t=2

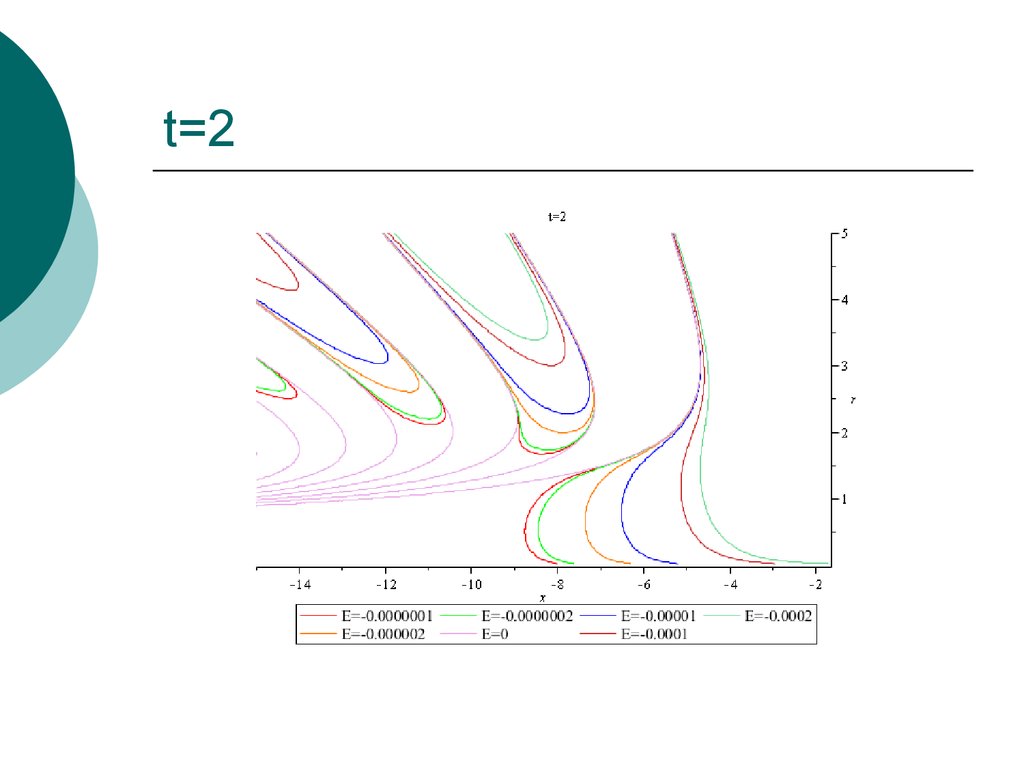
36. t=2

37. Вывод:

Была дана исчерпывающая информация о
фундаментальном решении E, прослежена
эволюция поверхностей уровня во времени
и выявлены интересные физические
эффекты(существование торроидалольных
стратов)

38. Спасибо за внимание