Похожие презентации:
Решение задач С2. Плоскость
1. Решение задач С2
Титенко О.Г. учитель математики МБОУ СОШ № 17с. Краснопартизанского
2. Вариант 21
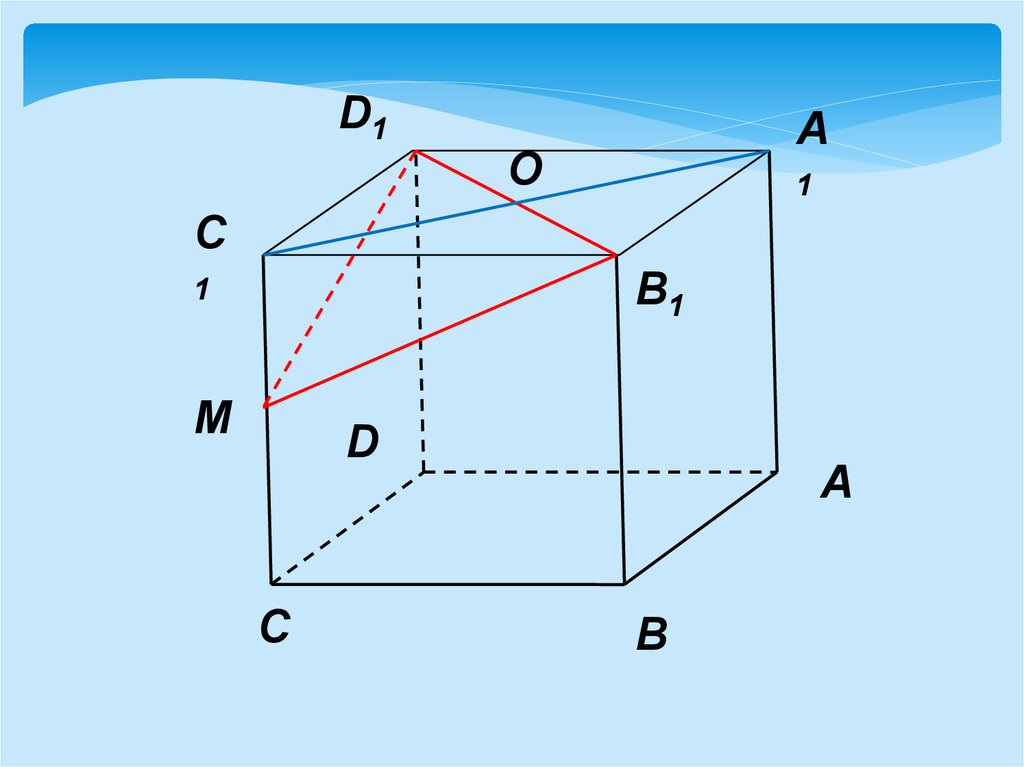
В основании прямой призмыABCDA1B1C1D1 лежит ромб ABCD, со
стороной a и острым углом А, равным
600. Высота призмы равна a. Через
вершины B1, D1 и середину М ребра
СС1 проведена плоскость. Найдите
угол ( в градусах) между плоскостью
B1MD1 основанием ABCD.
3.
D1A
O
1
C
B1
1
M
D
C
A
B
4.
Плоскости АВС и А1В1С1 параллельны. ПлоскостьB1MD1 образует равные углы с плоскостями
оснований призмы. Находим двугранный угол
C1B1D1M
MC 1 ( B1C 1 D1)
Т.к.
ОC1 B1D1
и МО B1D1
, то
по теореме
о 1трех перпендикулярах
МОС
.
Значит
угла C1B1D1M
- линейный угол двугранного
5.
С1В1О прямоуголь ный,В1С1О 30 ,
0
В1С1 a,
a 3
C1O B1C1 cos 30
2
С1MО прямоуголь ный,
0
C 1M a a 3
1
tg C1OM
:
C1O 2 2
3
0
C1OM 30
6. Вариант 23
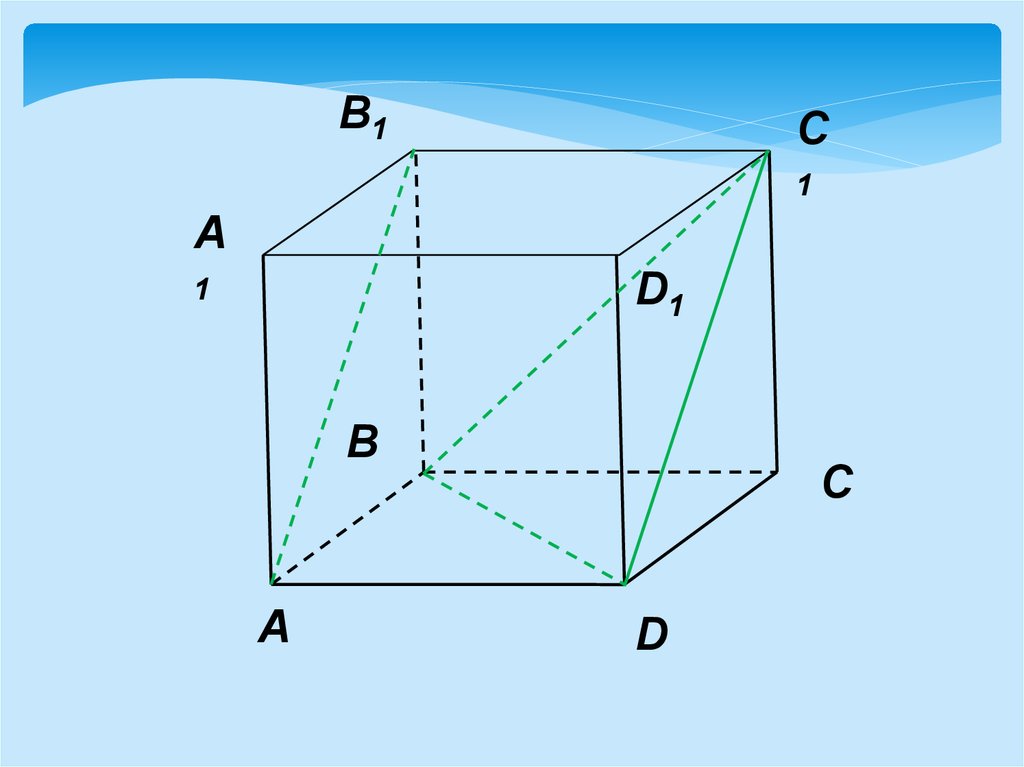
В основании прямой призмыABCDA1B1C1D1 лежит ромб ABCD,
со стороной a и острым углом А,
равным 600. Высота призмы равна
a. Найдите косинус угла между
прямыми АВ1 и ВD
7.
B1C
1
A
D1
1
B
A
C
D
8.
Прямые АВ1 и BD – скрещивающиеся, т.к. АВ1 иDC1 параллельные прямые, то угол BDC1 –
искомый угол между скрещивающимися прямыми
АВ1 и BD .
BDC 1 равнобедренный,
BC 1 DC 1 a 2
BD a
9.
По теореме косинусов:BC 1 BD DC 1 2 BD DC 1 cos BDC 1
2
2
2
BD DC 1 BC 1
cos BDC 1
2 BD DC 1
a 2 2a 2 2a 2
1
2
cos BDC 1
4
2a a 2
2 2
2
2
2
10. Вариант 25
В основаниипрямой
призмы
3
ABCDA1B1C1D1 лежит ромб ABCD,
со стороной
и острым углом
А, равным 600. Высота призмы
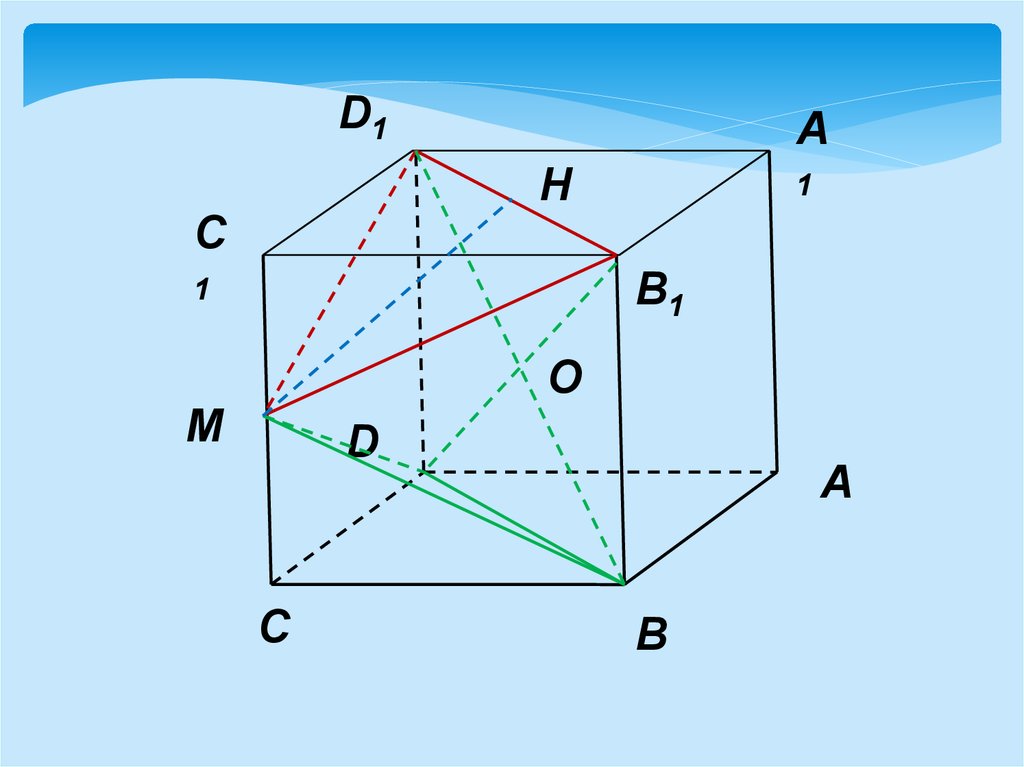
равна 4. Через вершины B1, D1 и
середину М ребра СС1 проведена
плоскость. Найдите расстояние от
точки В до плоскости B1MD1.
11.
D1A
Н
1
C
B1
1
О
М
D
C
A
B
12.
B1C1M D1C1M BCM DCMB1M D1M BM DM 2
2
3
2
7
Рассмотрим пирамиду MDD1B1B. Т.к. боковые
ребра пирамиды равны, то основанием высоты,
проведенной из вершины М к основанию
пирамиды – прямоугольнику DD1B1B, является
точка О ( точка пересечения диагоналей
основания).
Вычислим объём пирамиды MDD1B1B.
13.
1VMDD1 B1 B SDD1 B1 B MO
3
DB 3
D1D 4
SDD1 B1 B DB D1D 4 3
BD 1
3 4
19
BO
2
2
2
19
14.
219
2
3
7
MO
2
2
3
1
VMDD1 B1 B 4 3 2 3
2
3
1
VMD1 B1 B VMDD1 B1 B 3
2
Объём пирамиды MD1B1B можно вычислить
приняв за основание треугольник MD1B1. Высота,
проведенная из вершины В к основанию MD1B1,
является искомым расстоянием от точки В до
15.
MD1B1 равнобедренный,MB1 МD1 7
B1D1 3
3
D1H B1H
2
MH
2
3
5
7
2
2
2
1
1
5 5 3
S MD1 B1 B1D1 MH 3
2
2
2
4
16.
1VMD1 B1 B SMD1 B1 h
3
3 V
3 3 12
h
2,4
SMD1 B1 5 3
5
4
17. Вариант 27
Восновании
прямой
призмы
ABCA1B1C1 лежит равнобедренный
прямоугольный
треугольник
с
катетом 1.
Высота призмы СС1 равна 2.
Найдите
косинус
угла
между
прямыми AB1 и BC1.
18.
С1А1
В1
С
А
В
О
19.
Прямыеплоскости
AB1
АА1В
и
BC1 – скрещивающиеся. В
проведем
прямую
ВО
параллельную прямой АВ1.
Угол ОВС1 является углом между прямыми АВ1 и
АВС прямоуголь ный
ВС1.
АВ 2
СС1В прямоуголь ный
С1В 5
ОАВ1В параллелограмм
ОА ВВ 1 2
20.
ОА1С1 прямоуголь ныйОС 1 17
ABB1 прямоуголь ный
АВ1 6
ОВ АВ1 6
В ОВС 1 по теореме косинусов
ОС 1 ОВ ВС 1 2 ОВ ВС 1 соs OBC 1
2
2
2
ОВ ВС 1 ОС 1
соs OBC 1
2 ОВ ВС 1
2
2
2
21.
6 5 172
соs OBC 1
2
2
2 6 5
6 5 17
6
3
соs OBC 1
2 30
2 30
30
OBC 1 является тупым углом.
За угол между прямыми АВ1 и ВС1
нужно принять угол , смежный OBC 1
cos(1800 ) cos
3
cos
0,3
30
22. Вариант 29
В основании прямой призмы лежитпрямоугольный
треугольник
с
катетами 3 и 4. Через гипотенузу АВ
основания и середину М ребра СС1
проведена плоскость.
При какой длине высоты призмы
плоскость
АМВ
наклонена
к
плоскости основания под углом 450?
23.
С1А1
В1
М
С
А
Н
В
24.
АС ВС 4 3СН АВ, СН
2,4
АВ
5
0
0
МСН , МСН 90 , МНС 45 ,
МСН равнобедренный, МС НС 2,4
МС МС 1 2,4
СС1 4,8





















 Математика
Математика








