Похожие презентации:
График функции y = x 2
1.
2.
Как называется график функции y = x 2?Сформулируйте свойства функции y = x
Как называется точка пересечения
параболы y = x 2
с её осью симметрии ?
2
3.
y ax2
4. Наша задача:
Рассмотреть графики функций y = ax2.Изучить свойства функции y = ax2
Научиться строить графики
функции y = ax2
5.
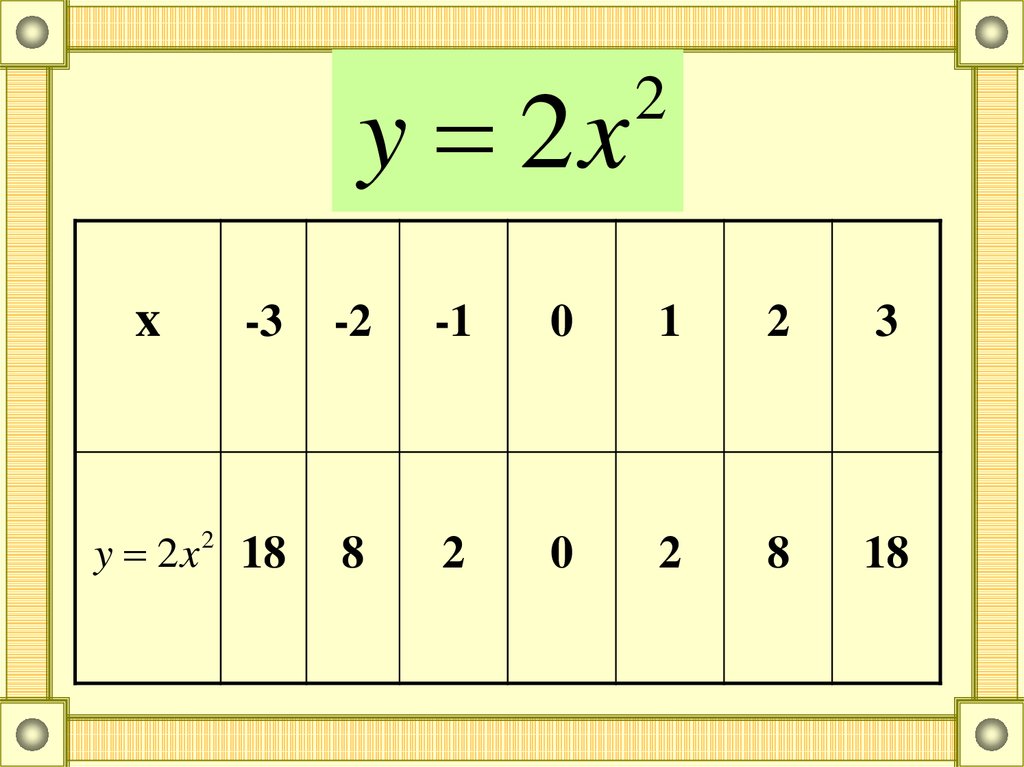
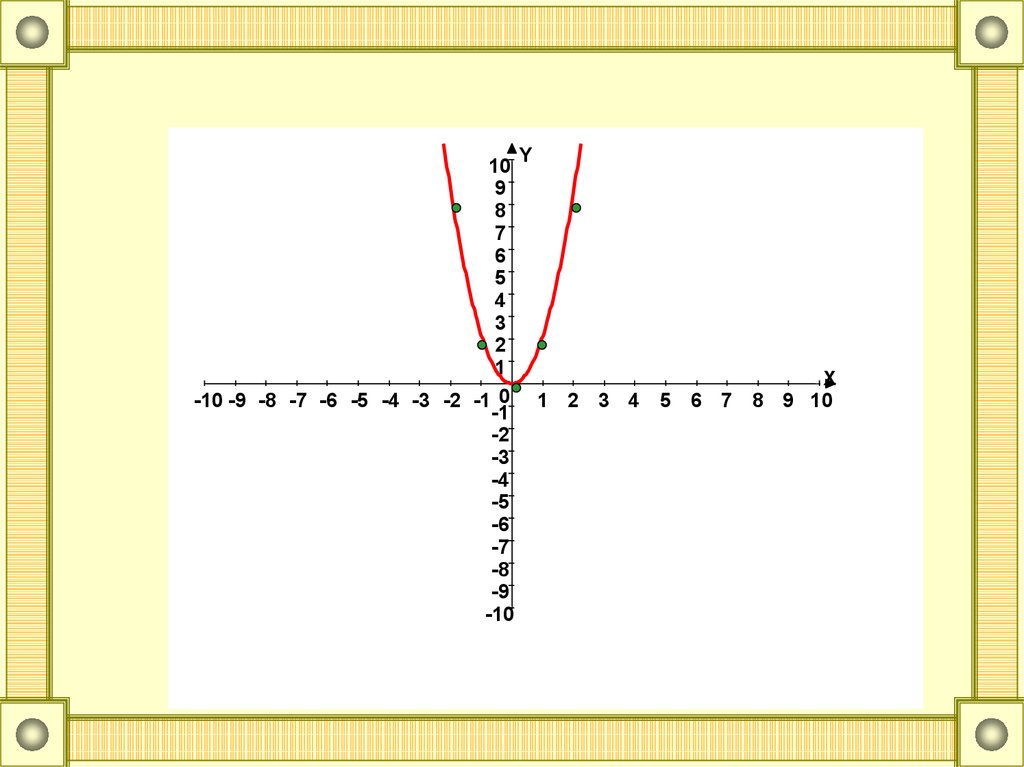
y 2xx
2
-3
-2
-1
0
1
2
3
y 2x 2 18
8
2
0
2
8
18
6.
109
8
7
6
5
4
3
2
1
-10 -9 -8 -7 -6 -5 -4 -3 -2 -1 0
-1
-2
-3
-4
-5
-6
-7
-8
-9
-10
Y
1 2
3 4
5
6 7
X
8 9 10
7.
10Y
y=2x2
9
8
7
6
5
y=x2
4
3
2
1
-10
-9
-8
-7
-6
-5
-4
-3
-2
-1
0
-1
X
1
2
3
4
5
6
7
8
-2
-3
-4
-5
-6
-7
-8
График функции y = 2x2 получается
растяжением
-9
графика функции y = x2 от-10оси Ox вдоль оси Oy
в 2 раза.
9
10
8.
y 1/ 2x2
x
-3
-2
-1
0
1
2
3
y 1/ 2x2
4,5
2
0,5
0
0,5
2
4,5
9.
10Y
y=x2
9
8
7
6
5
4
y = ½ x2
3
2
1
-10
-9
-8
-7
-6
-5
-4
-3
-2
-1
0
-1
X
1
2
3
4
5
6
7
8
9
10
-2
-3
-4
-5
-6
-7
-8
-9
-10
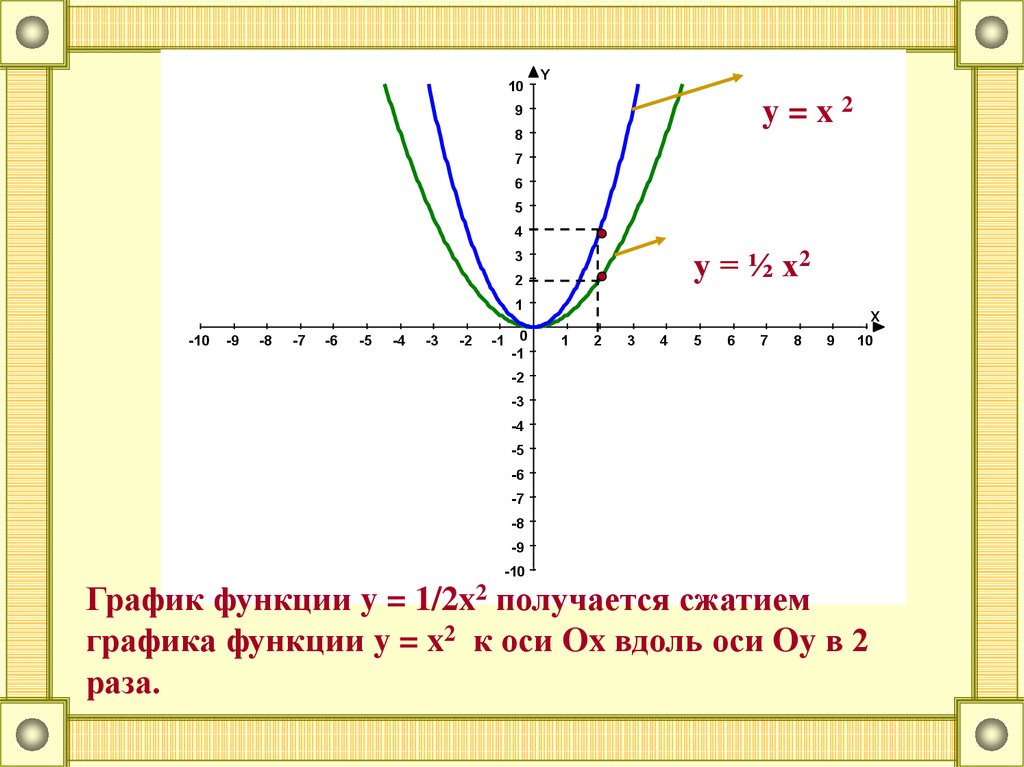
График функции y = 1/2x2 получается сжатием
графика функции y = x2 к оси Ox вдоль оси Oy в 2
раза.
10.
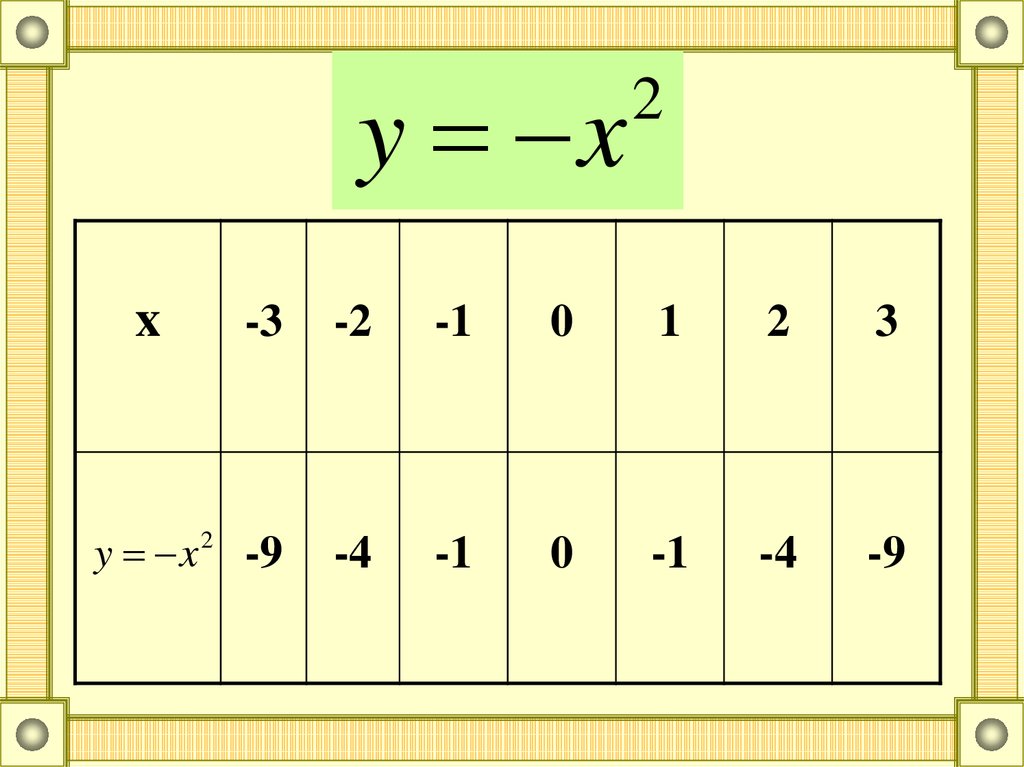
y xx
2
-3
-2
-1
0
1
2
3
y x 2 -9
-4
-1
0
-1
-4
-9
11.
10Y
9
8
7
y=x2
6
5
4
3
2
1
-10
-9
-8
-7
-6
-5
-4
-3
-2
-1 0
-1
X
1
2
3
4
5
6
7
8
9
10
-2
-3
-4
-5
-6
y=-x2
-7
-8
-9
-10
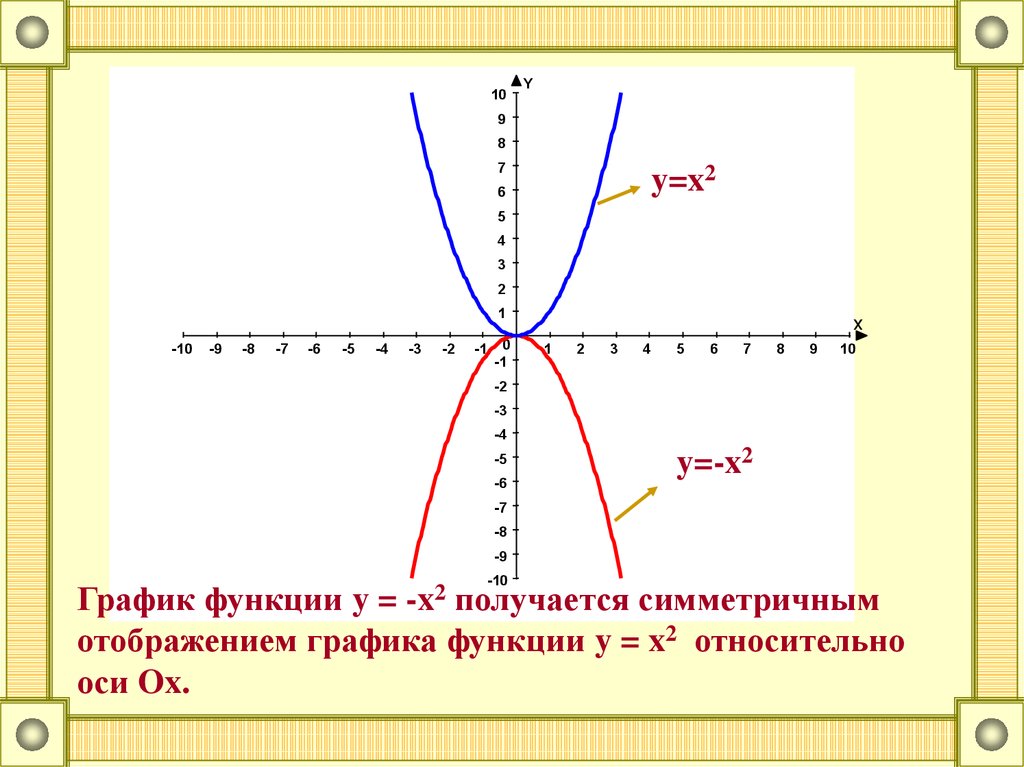
График функции y =
получается симметричным
отображением графика функции y = x2 относительно
оси Ox.
-x2
12.
Вывод:График функции y = a x 2 при любом
a ≠ 0 также называется параболой.
При a > 0 ветви параболы направлены
вверх,
а при a < 0 ветви параболы
направлены вниз.
13.
С помощью графика функции y = -2x2 решитьнеравенство: - 2 x2 ≤ - 8
10
Y
Ответ: x € (- ∞; - 2] U [2; +∞)
9
8
7
6
5
4
3
2
1
-10 -9
-8
-7
-6
-5
-4
-3
-2
-1 0
-1
X
1
2
3
4
5
6
7
8
9
-2
-3
-4
y = -2x2
-5
-6
-7
-8
-9
-10
y=-8
10
14.
№ 599 (3)15.
§37 № 59516.
17.
Хочется надеяться, чтосегодняшний урок
разбудит у вас жажду
новых познаний, ведь
«великий океан
истины по-прежнему
расстилается перед
вами не
исследованным до
конца».


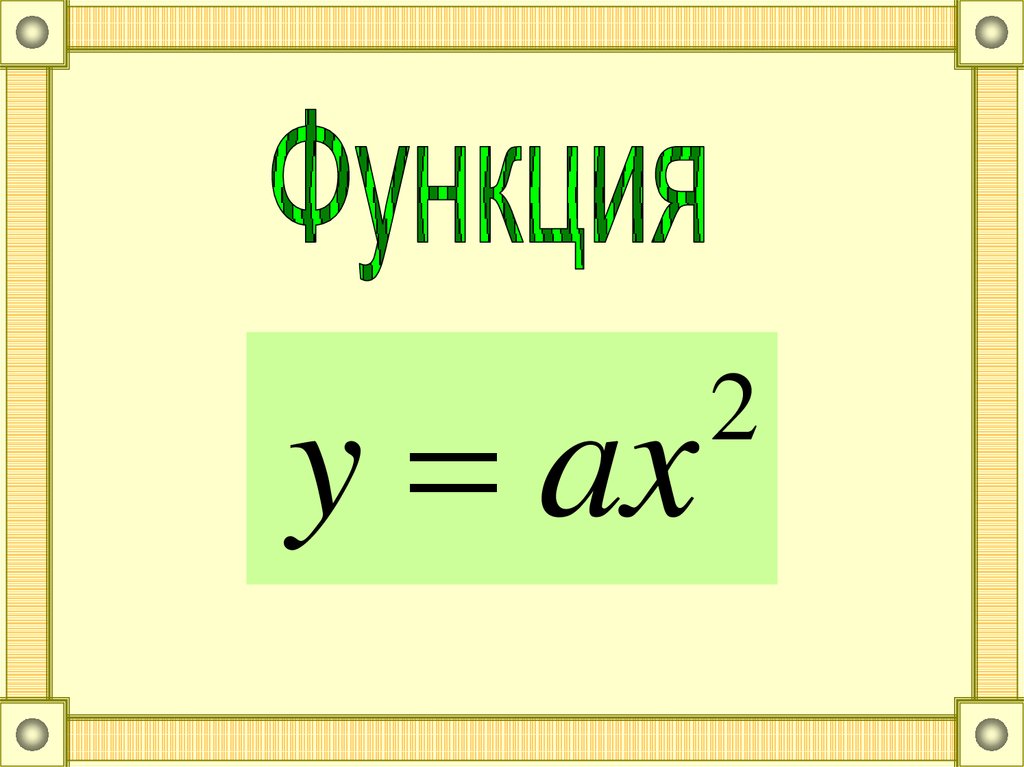









 Математика
Математика








