Арифметический квадратный корень

1. Арифметический квадратный корень

Понятие квадратного корня
из неотрицательного числа

2.

у
у = х2
А
В
4
1
-2
0
у=4
х
1 2
Решить уравнение
х2 = 4
Построим в одной системе
координат
параболу у = х2 и прямую у = 4
Абсциссы точек А и В
являются корнями уравнения,
т.е. х1 = – 2, х2 = 2
Ответ: – 2; 2

3.

9
у
C
D
у=9
у = х2
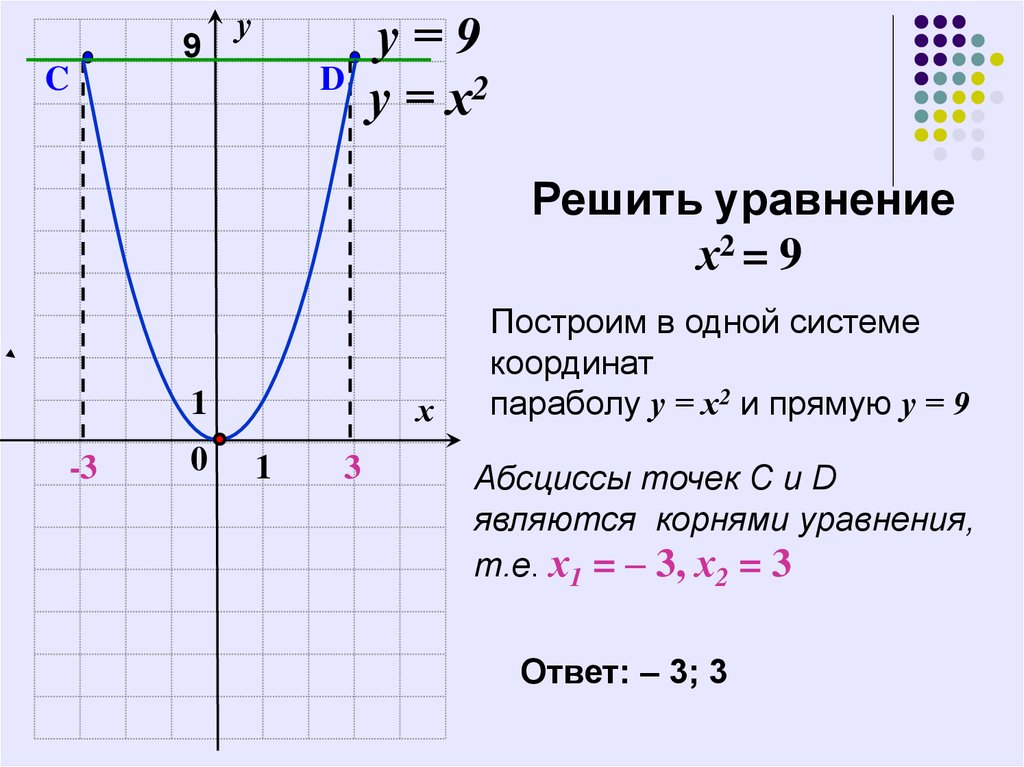
Решить уравнение
х2 = 9
1
-3
0
х
1
3
Построим в одной системе
координат
параболу у = х2 и прямую у = 9
Абсциссы точек C и D
являются корнями уравнения,
т.е. х1 = – 3, х2 = 3
Ответ: – 3; 3

4.

у
у = х2
C
5
1
5
0
у=5
D
2 3
1
5
х
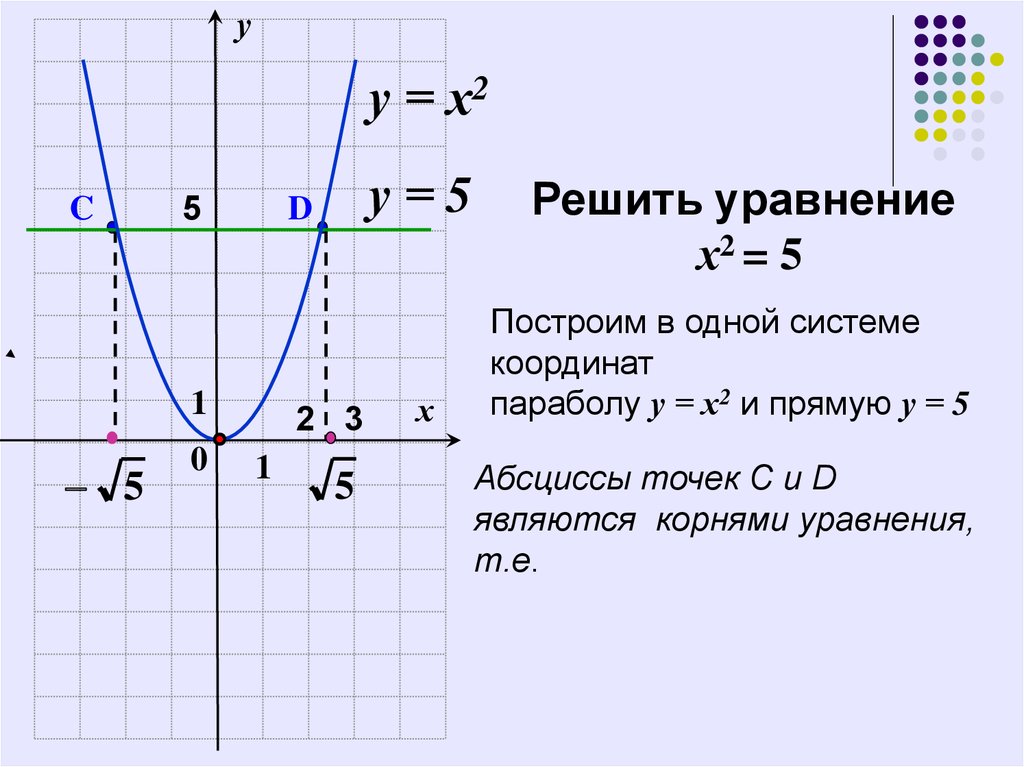
Решить уравнение
х2 = 5
Построим в одной системе
координат
параболу у = х2 и прямую у = 5
Абсциссы точек C и D
являются корнями уравнения,
т.е.

5.

у
у = х2
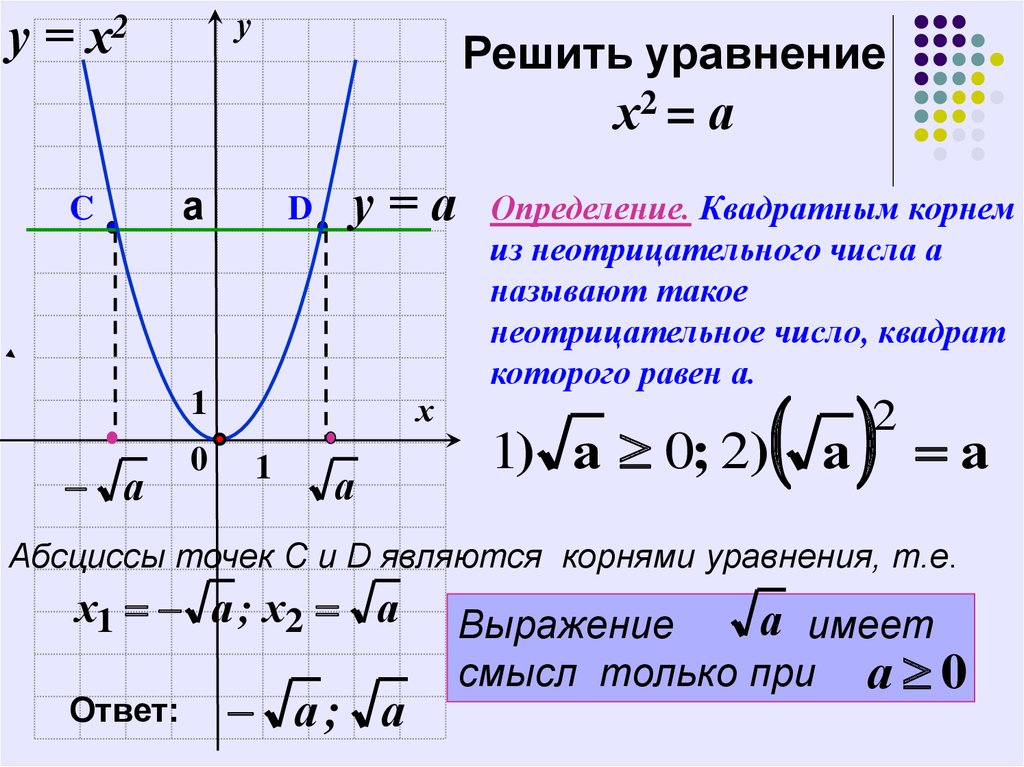
Решить уравнение
х2 = а
C
а
D
у=а
1
а
0
х
1
а
Определение. Квадратным корнем
из неотрицательного числа а
называют такое
неотрицательное число, квадрат
которого равен а.
1) а 0; 2) а
2
а
Абсциссы точек C и D являются корнями уравнения, т.е.
х1 а ; х2 а
Ответ:
а; а
а имеет
Выражение
смысл только при а 0

6.

Обозначается:
- знак корня
(радикал)
a
a
- подкоренное число
(выражение)
Область допустимых значений
переменной (ОДЗ) арифметического
квадратного корня:
a≥0
20.07.2019
6

7.

Операция нахождения квадратного
корня из неотрицательного числа
называют извлечением квадратного
корня.

8.

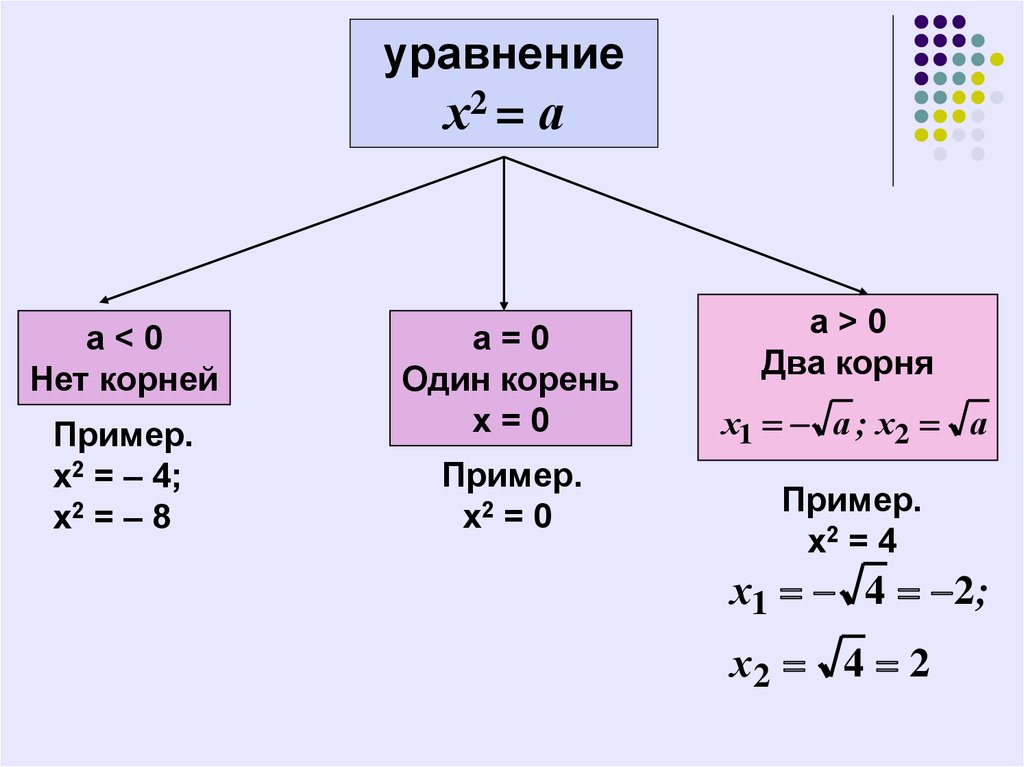
уравнение
х2 = а
a<0
Нет корней
Пример.
х2 = – 4;
х2 = – 8
а=0
Один корень
х=0
Пример.
х2 = 0
а>0
Два корня
х1 а ; х2 а
Пример.
х2 = 4
х1 4 2 ;
х2 4 2

9.

Извлечь арифметический квадратный
корень:
2
49 7 , так как 7 0 ; 7 49
0,25 0,5
0
0
17 4,123
4
Выражение не имеет смысла
961 31
5625 75