Асимптотические методы. Граничные условия на горизонтальной скважине. (Лекция 3)

1. Введение в асимптотические методы. Лекция 3: продолжение

Граничные условия на
горизонтальной скважине

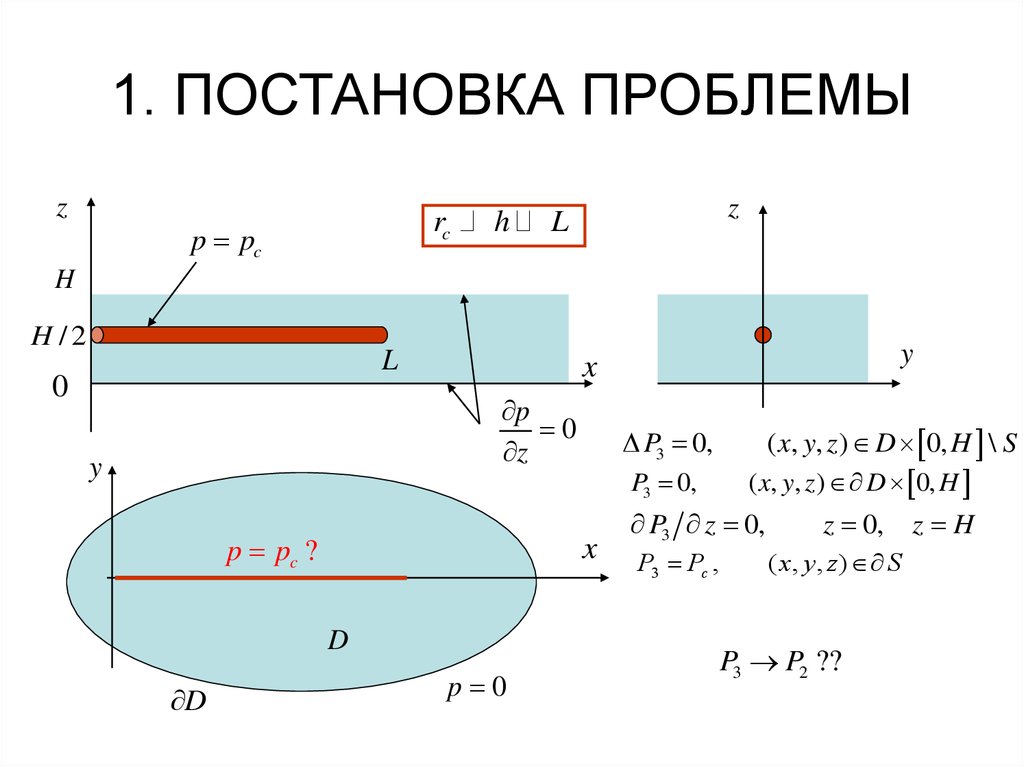
2. 1. ПОСТАНОВКА ПРОБЛЕМЫ

z
rc
p pc
h
z
L
H
H /2
L
0
p
0
z
y
p pc ?
P3 0,
P3 0,
x
D
D
y
x
p 0
( x, y, z ) D 0, H \ S
( x, y, z ) D 0, H
P3 z 0,
P3 Pc ,
z 0,
( x, y , z ) S
P3 P2 ??
z H

3. 2. ТЕХНИКА

L
L
P2 ( x, y ) G2 ( x, y; x, 0) q( x) dx
P3 (r ) G3 ( x, y, z; x,0, H / 2)q ( x)dx
10
G2 ( x x) ( y y)
H
G2 0,
( x, y) D
G3 ( x x) ( y y ) ( z z )
0
( x, y, z ) D 0, H
G3 0,
G3 z 0,
L
P3 P2 R( x, y, z; x, 0, H 2) q( x) dx
z 0, z H
R G3 G2
0
R ( x x) ( y ) z H 2 1 H
R z 0,
R 0,
z 0, z H
y 2 ( x x) 2
1
R
H
Преобразование
Фурье
2 n y 2 ( x x) 2
2 n
cos
z H 2 K0
H
H
n 1
q
L
0
Pc P2 R ( x, 0, rc H 2; x, 0, H 2) q( x) dx q ( x) f ( x ) dx
1
f ( x x)
H
cos 2 n r
n 1
c
H K0 ( 2 n x x H )
1 H
ln
2 2 rc
f
x
H
x

4. 3. РЕЗУЛЬТАТ

2 P2 0,
P2 0,
( x, y) D
( x, y) D
P2 n H 1q( x), y 0, 0 x L
Пример:
L1 L2 50 м
q2
P
Pc P2 2
n
H 10 м
H H
ln
2 2 rc
rc 0.1 м
1 % 2 %
q0
q1
100
17.54
17.37
21.03
1.01
19.8
50
20.54
20.30
25.56
1.19
24.4
10
28.41
27.91
40.29
1.78
41.81
2
34.13
33.27
58.69
2.49
72
0.5
36.44
35.22
74.53
3.35
104
H
2