Похожие презентации:
Линейные дифференциальные уравнения первого порядка
1. Тема :
Линейныедифференциальные
уравнения первого порядка
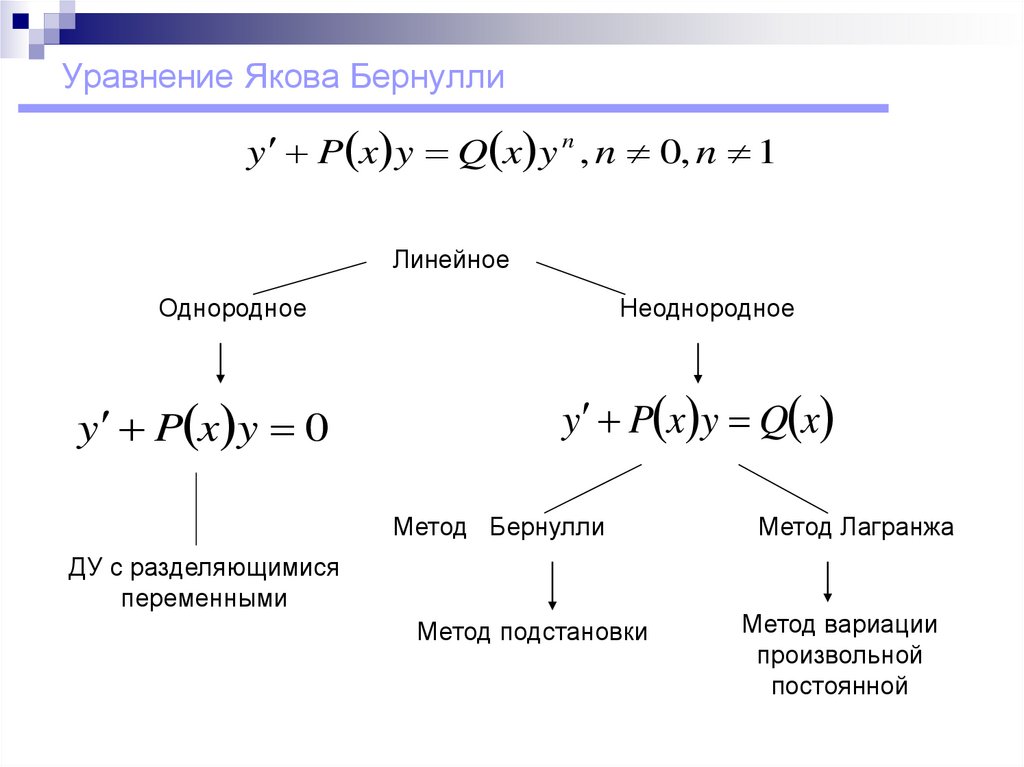
2. Уравнение Якова Бернулли
y P x y Q x y n , n 0, n 1Линейное
Однородное
y P x y 0
Неоднородное
y P x y Q x
Метод Бернулли
ДУ с разделяющимися
переменными
Метод подстановки
Метод Лагранжа
Метод вариации
произвольной
постоянной
3. Линейные дифференциальные уравнения первого порядка
Уравнение вида y P x y Q x ,Q x
P x
– функции постоянные величины, называется линейным
дифференциальным уравнением первого порядка
•Замечание. Уравнение называется линейным, так как искомая функция y
и её производная y’ входят в это уравнение в первой степени.
Линейное ДУ первого порядка называется однородным, если функция
Q x 0
Линейное ДУ первого порядка называется неоднородным, если
функция Q x 0
4. Линейное однородное ДУ первого порядка
1. Решить уравнениеРешение:
y
dy
,
dx
y y sin x 0
имеем
dy
y sin x 0
dx
Получаем
dx
y
dy
y sin xdx
ln y cos x C
Решение:
Выразить производную функции
через дифференциалы
Разделить переменные
dy
sin xdx 0
y
2. Решить уравнение
y P x y 0
y
0
x
y Cx
Интегрировать
(общее решение)
y
(общее решение)
5.
Линейное неоднородное ДУ. Метод Бернуллиy P x y Q x
Замечание. Любую величину можно представить в форме произведения двух
сомножителей, причем один из множителей можно выбрать по своему
желанию.
y u v v u.
y uv
В результате линейное неоднородное ДУ сводиться к двум уравнениям с
разделяющимися переменными.
где
u
и
v
- новые функции переменной
1. Решить уравнение
Решение:
Положим
тогда
y
3
y x.
x
3
P x , Q x x.
x
y uv,
y u v v u.
x
6. Алгоритм решения линейного ДУ первого порядка
y P x y Q xy uv, находят y u v v u
1. Приводят уравнение к виду
2. Используя подстановку
и подставляют эти выражения в уравнение.
3. Группируют члены уравнения, выносят одну из функций u или v
за скобки. Находят вторую функцию, приравняв выражение в скобках
нулю и решив полученное уравнение.
4. Подставляют найденную функцию в оставшееся выражение и
находят вторую функцию.
5. Записывают общее решение, подставив выражения для
найденных функций u и v в равенство y uv,
6. Если требуется найти частное решение , то определяют С из
начальных условий и подставляют в общее решение.
7.
Получимили
3
u v v u uv x,
x
3
u v v u v x.
x
3
v v 0.
x
dv
v ,
dx
dv 3dx
,
v
x
dv
dx
v 3 x ,
ln v 3 ln x,
v x3.
Имеем
u x 3 x
3
y x.
x
y uv
y
(1)
ЗП
y u v v u
Выразить производную функции
через дифференциалы
Разделить переменные
Интегрировать
С=0, ввиду произвольности в выборе
8.
uВыразить производную функции
через дифференциалы
du
dx
1
du 2 dx
x
du
Разделить переменные
dx
x2
1
u C,
x
Интегрировать
постоянную С писать обязательно!
Окончательно получим
1 3
y uv C x
x
(общее решение)
Замечание. Уравнение (1) можно было записать в эквивалентном
виде:
3
v u u uv x
x
=0
3
u v v u uv x,
x
Находим u из ур-ния, приравняв выражение в скобках к нулю. Затем,
находим V , решая уравнение u v =x
9. Самостоятельная работа
Решить уравнения:y 0 2.
1.
yy 2 0,
2.
xy y x 2 cos x.
Решить задачу Коши.
Найти общее решение.
3. Решить линейное ДУ первого порядка
2y
y
x2 , x 0
x
4. Решить задачу Коши для линейного ДУ первого порядка
y ytgx
1
; y 0 0
3
cos x








 Математика
Математика








