Применение определенного интеграла

1. Занятие 112. Применение определенного интеграла

Математика
Занятие 112.
Применение определенного
интеграла
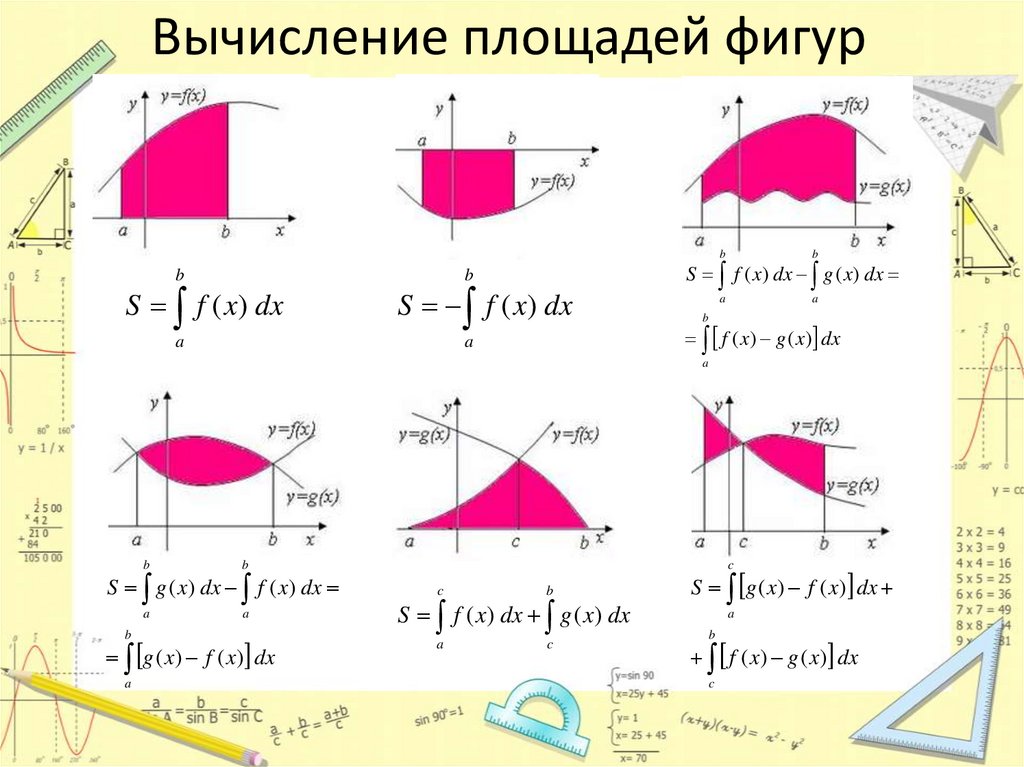
1. Вычисление площадей фигур
2. Вычисление объемов тел

2. Вычисление площадей фигур

Пусть на плоскости имеется некоторая
фигура, граница которой задана конечным
количеством непрерывных функций.
Для нахождения ее площади нужно
разделить исходную фигуру на несколько
криволинейных трапеций, площади
которых можно вычислить через
определенные интегралы.

3. Вычисление площадей фигур

b
S f ( x) dx
b
S f ( x) dx
a
a
b
b
a
a
S f ( x) dx g ( x) dx
b
f ( x) g ( x) dx
a
b
b
S g ( x) dx f ( x) dx
a
b
a
g ( x) f ( x) dx
a
c
c
b
S f ( x) dx g ( x) dx
a
c
S g ( x) f ( x) dx
a
b
f ( x) g ( x) dx
c

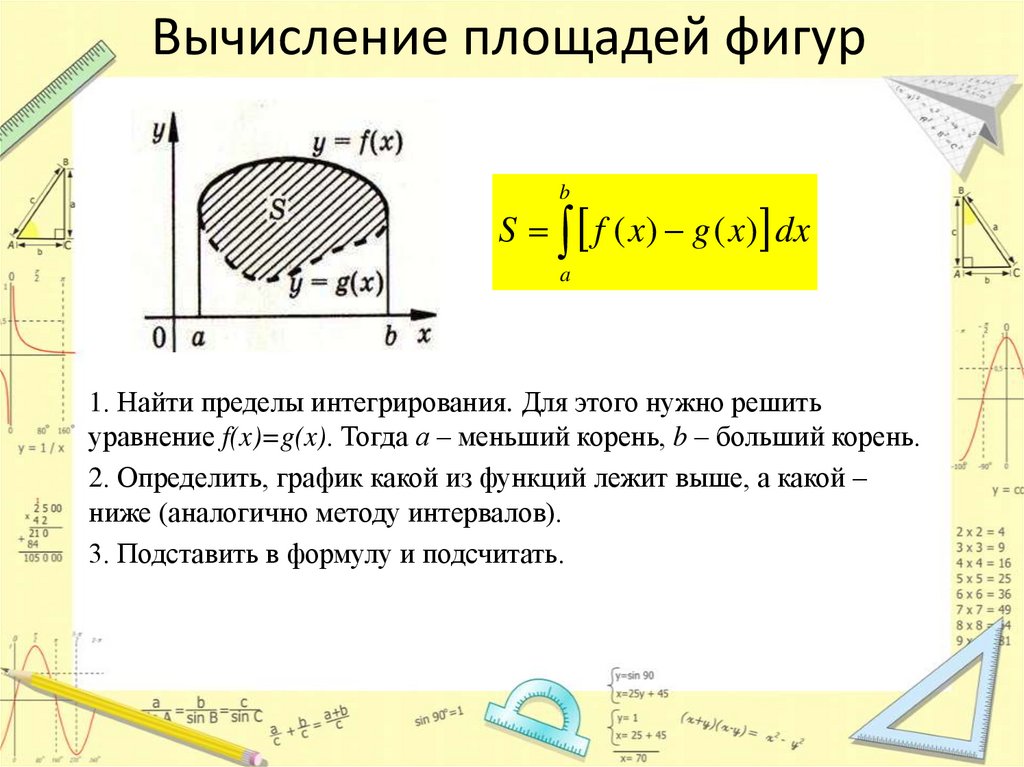
4. Вычисление площадей фигур

b
S f ( x) g ( x) dx
a
1. Найти пределы интегрирования. Для этого нужно решить
уравнение f(x)=g(x). Тогда а – меньший корень, b – больший корень.
2. Определить, график какой из функций лежит выше, а какой –
ниже (аналогично методу интервалов).
3. Подставить в формулу и подсчитать.

5. Вычисление площадей фигур

Найти площадь фигуры ограниченной линиями:
1)
y x 2 3, y 0, x 1, x 2
2
23
13
8
х3
1
S ( x 3) dx 3 х 3 * 2 3 *1 6 3
3
3
1
3
3
3
1
7 16
3
3 3
2
2
2)
y x 3 , y 4 x 1, x 0, x 1
t 1 / 2 [0; 1],
y1 (1 / 2) 3 1 / 8, y2 4 *1 / 2 1 1
g ( x) x 3 , f ( x) 4 x 1
1
х2
х4
S (4 х 1 x ) dx 4 * х
2
4
0
3
1
3
2 1 0
4
4
1
0
х4
2х х
4
2
1
0

6. Вычисление площадей фигур

Найти площадь фигуры ограниченной линиями:
3)
y x 2 2 х, y 0
x 2 2 х 0 x( х 2) 0 x 0 или х 2 0 х1 0, х2 2
a 2, b 0; t 1 [ 2; 0],
y ( 1) 2 2 * ( 1) 1
0
х3
х3
( 2) 3
х2 0
2
S ( x 2 x) dx 2 * х 0
( 2) 2
2 2
3
3
2
3
2
8
4
4
3
3
0
2

7. Вычисление площадей фигур

Найти площадь фигуры ограниченной линиями:
4)
y x2 , y х
x 2 х x 4 х x 4 х 0 x ( х 3 1) 0 x 0 или х 3 1 0
х1 0, х2 1 a 0, b 1;
t 1 / 4 [0; 1],
y1 (1 / 4) 2 1 / 16, y2 1 / 4 1 / 2
g ( x) x 2 , f ( x) х
1
3
2
х
S ( х x 2 ) dx
х3
3
3
0
1
0
2 1 1
3 3 3

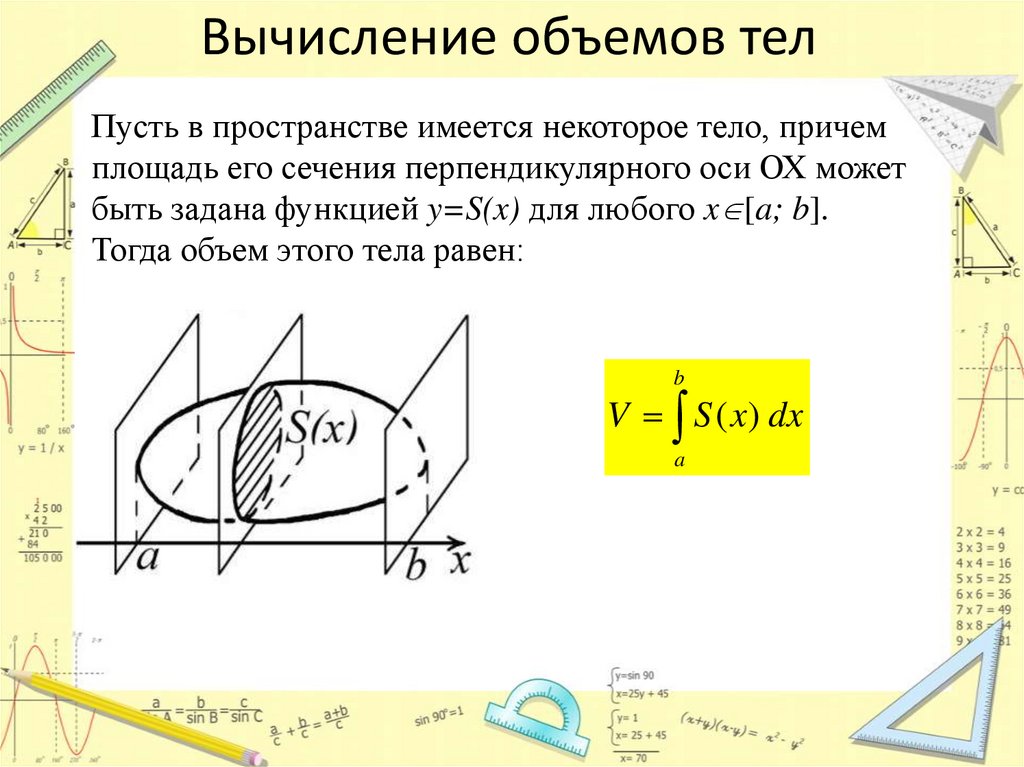
8. Вычисление объемов тел

Пусть в пространстве имеется некоторое тело, причем
площадь его сечения перпендикулярного оси ОХ может
быть задана функцией y=S(x) для любого x [a; b].
Тогда объем этого тела равен:
b
V S ( x) dx
a

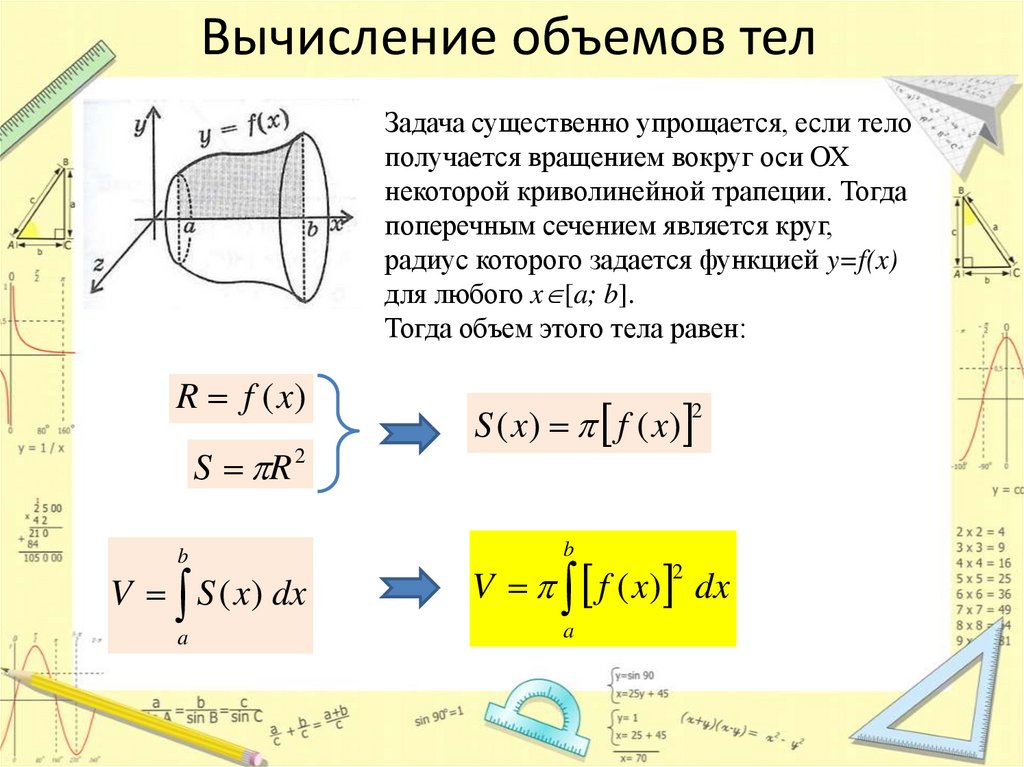
9. Вычисление объемов тел

Задача существенно упрощается, если тело
получается вращением вокруг оси ОХ
некоторой криволинейной трапеции. Тогда
поперечным сечением является круг,
радиус которого задается функцией y=f(x)
для любого x [a; b].
Тогда объем этого тела равен:
R f (x)
S R 2
b
V S ( x) dx
a
S ( x) f ( x)
2
b
V f ( x) dx
2
a

10. Вычисление объемов тел

Вычислить объем тела, полученного вращением вокруг
оси ОХ криволинейной трапеции, заданной линиями:
b
1)
y x 1, y 0, x 1, x 2
2
V f ( x) dx
2
a
х5
2
х3
V ( x 1) dx ( x 2 x 1) dx 2 * х
3
5
1
1
1
2
2
2
2
4
2
25
15
23
13
1 2 178
32 16
2 * 2 2 * 1 2 1
3
3
3
5 3
15
5
5
5
2)
y 12 x 5 , y 0, x 0, x 1
1
х2
V ( 12 x 5 ) dx (12 x 5) dx 12 * 5 х
2
0
0
0
1
1
2
(6 х 5 х) 6 5 * 0
2
1
0

11. Вычисление объемов тел

Вычислить объем тела, полученного вращением вокруг
оси ОХ криволинейной трапеции, заданной линиями:
3)
b
V f ( x) dx
y 1 x , y 0
2
2
a
1 x 2 0 1 x 2 0 x 2 1 х1 1, х2 1
a 1, b 1
1
V 1 x2
1
2
3
1
х
2
dx (1 x ) dx х
3 1
1
1
13
( 1) 3
2 2 4
1 1
3
3
3 3 3