Похожие презентации:
Игры в нормальной форме. Normal form games, strategic form games
1. Игры в нормальной форме (normal form games, strategic form games)
1) Множество игроков I = {1 , 2 , … , n}2) Множества стратегий S1 , S2 , … , Sn
Пространство стратегий игры S = S1 S2 … Sn
3) Функции выигрышей
u1: S → ℝ1
u2: S → ℝ1
…
un: S → ℝ1
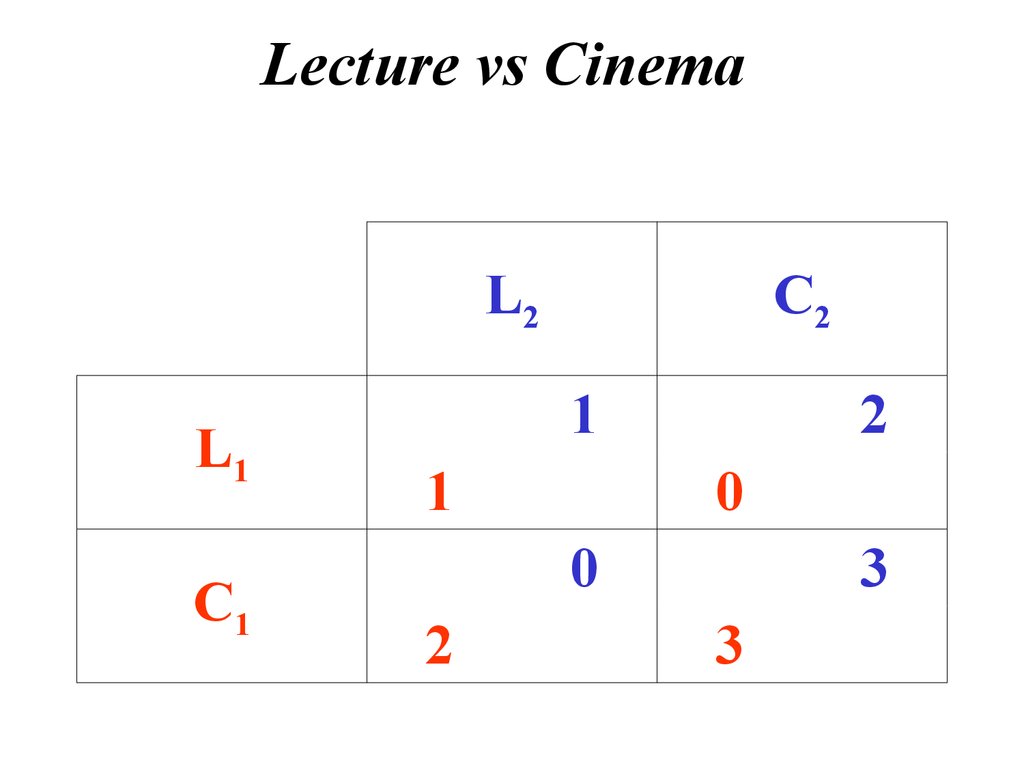
2. Lecture vs Cinema
L2L1
C1
C2
1
1
2
0
0
2
3
3
3. Полезные обозначения
G = {I ; S ; U}, гдеU: S → ℝn ; U = {u1 , u2 , … , un}
⊐ s = (s1 , s2 , … , sn) ∈ S, i ∈ I.
s–i ⇆ (s1 , s2 , … , si–1 , si+1 , … , sn) ∈ S–i
S–i ⇆ S1 S2 … Si–1 Si+1 … Sn
s = (si , s–i)
S = Si S–i
4. Игра 2 2
Игра 2 2s'2
s'1
s''1
s''2
u2(s'1;s'2)
u1(s'1;s'2)
u2(s'1;s''2)
u1(s'1;s''2)
u2(s''1;s'2)
u1(s''1;s'2)
u2(s''1;s''2)
u1(s''1;s''2)
5. Доминирование стратегий
⊐ G = {I ; S ; U}, i ∈ I.Стратегия s'i доминирует стратегию s''i игрока i,
если
ui (s'i , s–i) > ui (s''i , s–i) для ∀s–i ∈ S–i .
Обозначение
s'i ≻≻ s''i
{ui }
NB s'i ≻≻ s''i ⇔ (s'i , s–i) (s''i , s–i)
для ∀s–i ∈ S–i
6. Доминантные стратегии
⊐ G = {I ; S ; U}, i ∈ I.Стратегия s∗i называется
доминантной стратегией игрока i, если
ui (s∗i , s–i) > ui (si , s–i)
для ∀si ∈ Si , si ≠ s∗i и для ∀s–i ∈ S–i .
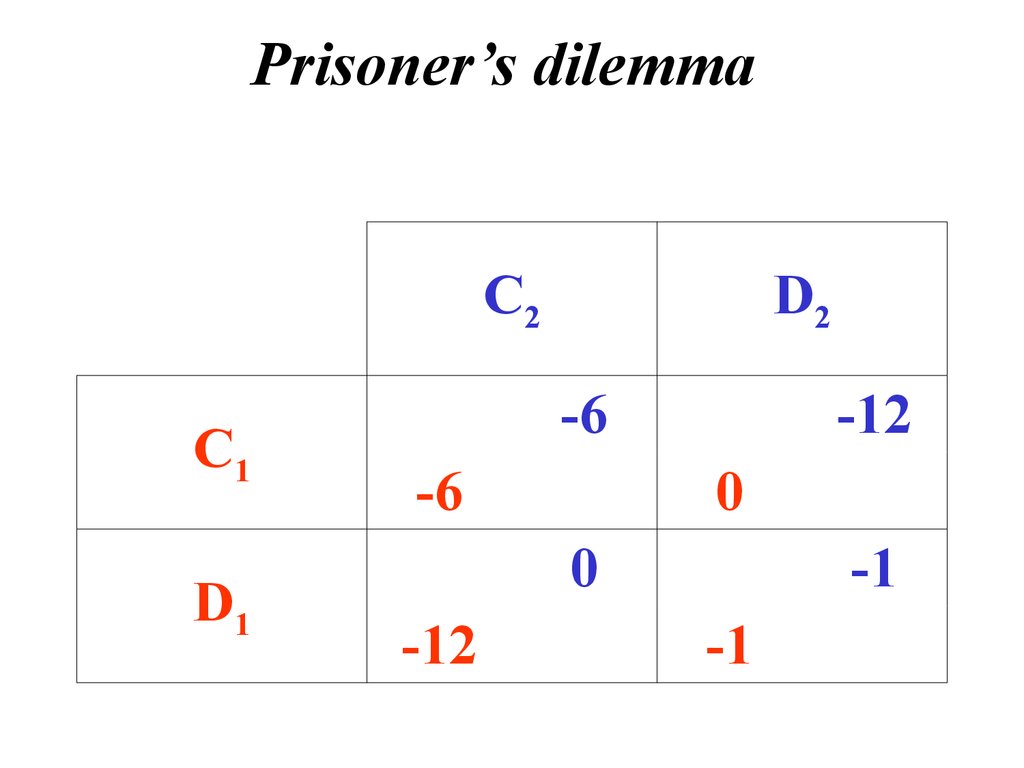
7. Prisoner’s dilemma
C2C1
D1
D2
-6
-6
-12
0
0
-12
-1
-1
8. Последовательное исключение доминируемых стратегий
LU
M
D
C
3
2
0
3
4
1
1
2
6
2
7
0
R
2
4
2
1
8
3
9. Общее знание (common knowledge)
⊐ G = {I ; S ; U}А является общим знанием, если
1) всем игрокам известно А
2) всем игрокам известно 1)
3) всем игрокам известно 2)
и т.д.
10. Игры с полной информацией (complete information games)
Игра G = {I ; S ; U} называется игрой с полнойинформацией, если набор функций выигрыша
U является общим знанием всех игроков.
В противном случае G называется игрой с
неполной информацией.








 Математика
Математика Программирование
Программирование








