Похожие презентации:
Выпуклый анализ. Пространство подмножеств. Лекция 1
1. ВЫПУКЛЫЙ АНАЛИЗ
ЛЕКЦИЯ 11. ПРОСРАНСТВО ПОДМНОЖЕСТВ
R
n
2.
ЛИТЕРАТУРА1. Благодатских В.И. Введение в оптимальное управление, М. Высшая школа 2001.
2. Васильев Ф.П. Численные методы решения экстремальных задач, М.: Наука, 1988.
3. Рокафеллер Р. Выпуклый анализ, М.: Мир, 1973.
4. Пшеничный Б.Н. Выпуклый анализ и экстремальные задачи, М.: Наука, 1979.
5. Алексеев В.М., Тихомиров В.М., Фомин С.В. Оптимальное управление,
М.: Наука, 1979.
6. Лутманов С.В. Курс лекций по методам оптимизации. Ижевск, РХД, 2001
3.
Rn .1. ПРОСРАНСТВО ПОДМНОЖЕСТВ
1.1. Пространство
n
R .
1.2. Точки и подмножества пространства
n
R .
4.
1. ПРОСРАНСТВО ПОДМНОЖЕСТВ1.1. Пространство
R
n
æ u1 ö
ç ÷
u = çL ÷.
ç un ÷
è ø
- двухмерная плоскость и т.д.
R
n
В частности
Элементы
заглавными.
Rn
а во втором
сложения векторов
R
1
числовая ось,
R2
будем обозначать строчными буквами,
При этом будем различать одноточечные
n
R . В первом случае это будет
n
u Î R n . В пространстве R определены операции:
множества и точку этого множества, как элемент
{ u} Ì R n ,
R .
R n . Рассмотрим n мерное евклидово векторное пространство
с элементами
а подмножества
n
æ u1 ö æ v1 ö
u + v = çç L ÷÷ + çç L ÷÷ =
ç u n ÷ ç vn ÷
è ø è ø
æ u1 + v1 ö
ç
÷
ç L ÷;
ç u n + vn ÷
è
ø
5.
умножение вектора на числоæ u1 ö
ç ÷
a ×çL ÷ =
ç un ÷
è ø
a ×u =
скалярное произведение векторов
æ a u1 ö
ç
÷
ç L ÷;
çaun ÷
è
ø
n
i i
u
u, v = å v .
i =1
Это пространство является нормированным с нормой
u =
u, u =
n
å( u )
i 2
.
i =1
Норма определяет расстояние между любыми двумя точками пространства
по формуле
r ( u, v ) = u v =
n
å( u
i =1
i
v
)
i 2
.
Rn
6.
1.2. Точки и подмножества пространстваn
R .
Определение 1. Открытой окрестностью точки
u0 Î R n
называется
множество
{
O ( u0 , R ) = u Î R
u0 R
Множество O
точке
Множество
u0 R
u0
( u0 , R )
и радиуса
{
}
u u0 < R ,
n
O ( u0 , R ) = u Î R
n
u0 Î R n , R > 0.
еще называют открытым шаром с центром в
R.
}
u u0 £ R ,
u0 Î R n , R > 0.
u0 Î R n .
По отношению к произвольному множеству U Ì R n можно определить
называют замкнутой окрестностью точки
точки
следующих четырех типов: внутренние, внешние, граничные и изолированные.
7.
Определение 2. Точкаесли
U
O ( v, e ) Ì U
v
O ( v, e )
v
называется внутренней точкой множества
для некоторого
U,
e > 0.
Определение 3. Совокупность всех внутренних точек множества
U
называется внутренностью множества
символом
U
и обозначается
int U .
Заметим, что не любое множество имеет непустую внутренность. Например,
плоский диск в трехмерном пространстве не имеет внутренних точек.
Определение 4. Множество состоящее только из внутренних точек называется
открытым множеством
Очевидно, что если внутренность множества не пуста, то она открыта.
Определение 5. Точка
множеству
U Ì Rn
v Î Rn
, если
называется внешней по отношению к
v U
и для некоторого
e >0
выполнено
8.
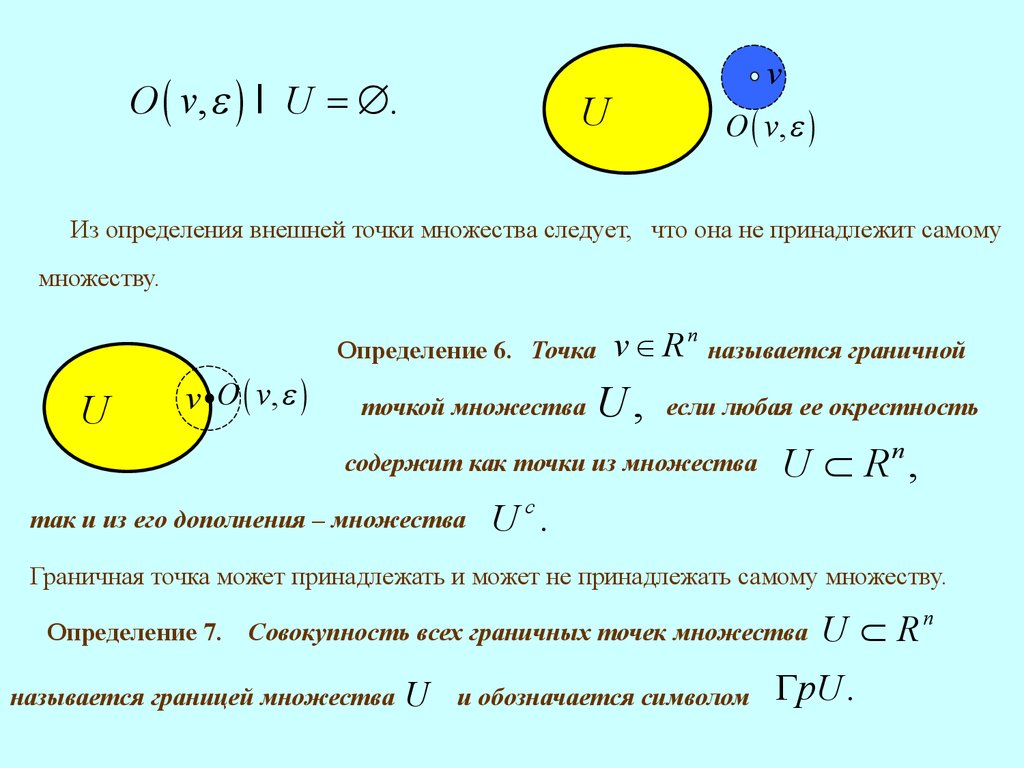
O ( v, e ) I U = Æ.v
U
O ( v, e )
Из определения внешней точки множества следует, что она не принадлежит самому
множеству.
Определение 6. Точка
U
v O ( v, e )
точкой множества
v ÎRn
U,
называется граничной
если любая ее окрестность
содержит как точки из множества
так и из его дополнения – множества
U Ì Rn ,
U c.
Граничная точка может принадлежать и может не принадлежать самому множеству.
Определение 7. Совокупность всех граничных точек множества
называется границей множества
U
и обозначается символом
U Ì Rn
GрU .
9.
Определение 8. ТочкаU,
v
U
O ( v, e )
Пусть
v Î Rn
если
O ( v, e ) ,
называется изолированной для множества
v ÎU
что
и существует такая окрестность
U I O ( v, e ) = { v} .
U Ì Rn.
Определение 9. Точка
u
называется предельной точкой множества
U,
если в любой открытой окрестности этой точки содержится хотя бы одна точка
множества
U.
Определение 10.
Множество
U Ì Rn
называется замкнутым, если оно
содержит все свои предельные точки.
Пересечение любого числа замкнутых множеств замкнуто. Это свойство позволяет
ввести следующее определение.
10.
Определение 11. ЗамыканиемU
замкнутое множество, содержащее
Заметим, что
Пример 1.
множества
U
называется наименьшее
U.
GрU = U \ int U .
Множество
O ( 0, R ) не является замкнутым,
æRö
ç ÷
0
точка ç ÷ O ( 0, R ) , хотя она является предельной
çL ÷
ç ÷
для множества O 0, R .
0
è ø
(
так как, например,
O ( 0, R ) .
)
Множество
{
}
O ( 0, R ) = u Î R n u £ R ,
замкнуто и
даже является замыканием множества
Кроме того, справедливо
R>0
O ( 0, R ) .
O ( 0, R ) .
11.
int éëO ( 0, R ) ùû = O ( 0, R ) ;1)
2)
{
Gр éëO ( 0, R ) ùû = S ( 0, R ) =
Определение 12. Множество
}
s Î R n s u0 = R .
U Ì Rn
называется ограниченным, если оно
содержится в замкнутом шаре
O ( 0, R )
конечного радиуса.
Определение 13. Множество U
называется компактным, если оно
U
R
O
ÌR
n
O ( 0, R )
замкнуто и ограничено.
Напомним, что из последовательности элементов компактного множества всегда
можно извлечь подпоследовательность,
множества.
сходящуюся к некоторому элементу этого
12.
Пример 2. Множество O ( u0 , r ) компактно. Множествокомпактным, т.к. оно не замкнутое.
множеством,
Пусть
O ( 0, R ) не является
Прямая на плоскости не является компактным
т.к. это неограниченное множество.
U Ì Rn
компактное множество.
Определение 14. Величина
U = max u
uÎU
называется модулем множества
В силу непрерывности функции нормы и компактности множества
max в принятом определении корректна.
операция
Геометрический смысл модуля множества
таков: это есть радиус наименьшего шара с центром в начале
U
O
U
U
координат,
содержащего это множество.
U Ì O ( 0, U ) .
Таким образом,
U.
13.
yУпражнение 1. Определить модуль круга
U=
{ ( x, y ) ( x x0 )
2
( x0 , y0 )
}
+ ( y y0 ) £ R 2 .
2
0
( x* , y* )
x
Решение:
U = x02 + y02 + R
y
Упражнение 2.
U=
{ ( x, y )
}
x x0 £ a, y y0 £ a .
( x0 , y0 )
0
Решение:
U =
( x* , y* )
Определить модуль квадрата
( x0 + a ) + ( y0 + a ) .
2
2
2a
2a
x













 Математика
Математика Программирование
Программирование








