Похожие презентации:
Дифференциальные уравнения и ряды. Лекция 8
1. Дифференциальные уравнения и ряды
Лекция 82.
Тема 2. Несобственные интегралыОпределенный интеграл
где [a, b] − конечный
промежуток интегрирования, а подынтегральная
функция f(x) непрерывна на отрезке [a, b], называют
еще собственным интегралом.
Определенный интеграл от непрерывной функции, но с
бесконечным промежутком интегрирования или
определенный интеграл с конечным промежутком
интегрирования, но от функции, имеющей на нем
бесконечный разрыв, называется несобственным
интегралом.
2
3.
§1. Несобственный интеграл I рода (интеграл сбесконечным промежутком интегрирования)
Пусть функция f(x) непрерывна на промежутке [a, +∞).
Если существует конечный предел
то его называют несобственным интегралом первого
рода и обозначают
Таким образом, по определению
3
4.
В этом случае говорят, что несобственный интегралсходится.
Если же указанный предел не существует или он равен
бесконечности, то говорят, что несобственный интеграл
расходится.
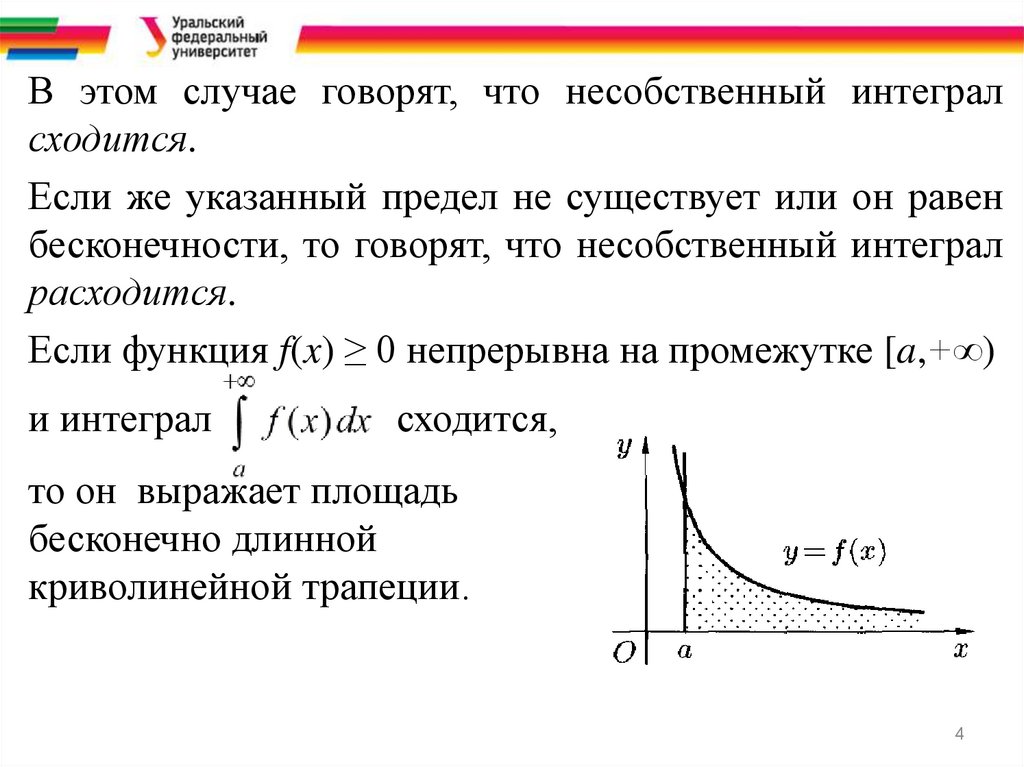
Если функция f(x) ≥ 0 непрерывна на промежутке [a,+∞)
и интеграл
сходится,
то он выражает площадь
бесконечно длинной
криволинейной трапеции.
4
5.
Аналогично определяется несобственный интеграл напромежутке (‒∞, b]:
Несобственный интеграл с двумя бесконечными
пределами определяется формулой:
где с ‒ произвольное число.
В этом случае интеграл слева сходится лишь тогда,
когда сходятся оба интеграла справа.
5
6.
Пример 1. Вычислить несобственные интегралы илиустановить их расходимость:
Решение.
1. Вычисляем по определению
1
b
dx
dx
1 lim 1 1
0 1 1.
lim 2 lim b
2
b
b x
b
x
x 1
1
b
Интеграл равен конечному числу сходится.
2. Решаем аналогично
1
1
1
dx
dx
lim ln x lim ln 1 ln a 0
x alim
a
a
x a
a
интеграл расходится.
6
7.
3. Разбиваем интеграл на сумму двух несобственныхинтегралов (для упрощения вычислений возьмем с = 0)
c
0
c
0
cos x dx cos x dx cos x dx cos x dx cos x dx.
Вычисляем первый интеграл
0
0
cos x dx lim cos x dx lim (sin x) a lim (sin 0 sin a)
0
a
a
a
a
lim sin a,
a
т.к. функция y = sin x не имеет предела при х , то
полученный предел не существует. Следовательно,
первый интеграл расходится. Значит cos x dx так же
расходится.
7
8.
При решении задач в некоторых случаях нетнеобходимости вычислять интеграл, достаточно лишь
знать сходится он или нет.
Для этого используются признаки сходимости:
1. Признак сравнения.
Если на промежутке [a, +∞) непрерывные функции f(x)
и g(x) удовлетворяют условию 0 ≤ f(x) ≤ g(x), то из
сходимости интеграла
интеграла
следует сходимость
а из расходимости интеграла
следует расходимость интеграла
8
9.
Пример 2. Исследовать на сходимостьРешение.
dx
Для сравнения используем интеграл 2 , который
x
1
сходится (см. пример 1).
Сравним подынтегральные функции:
1
1
1
x (1, ) 1 e 1
1 2
2.
x
x
1 e
x (1 e ) x
x
По признаку сравнения из сходимости большего
интеграла следует сходимость меньшего интеграла,
поэтому
1
dx
так же сходится.
2
x
x (1 e )
9
10.
2. Предельный признак сравненияЕсли на промежутке [a, +∞) f(x) > 0, g(x) > 0 и
существует конечный предел
интегралы
то
одновременно оба
сходятся или оба расходятся
(т.е. ведут себя одинаково в смысле сходимости).
В качестве интеграла, с которым производится
сравнение, обычно используют интегралы вида
которые сходятся при α > 1 и
расходятся при α ≤ 1.
10
11.
Пример 3. Исследовать на сходимостьРешение.
Подберем функцию для сравнения. Для этого
преобразуем подынтегральную функцию
x2 2
( x 2 1) 1
1
ln 2
ln
ln 1 2
.
2
x 1
x 1
x 1
Используем эквивалентные функции:
ln(1 x) x при х 0,
1
тогда ln 1 2
x 1
1
x2 1
1
при х .
2
x
Поэтому для сравнения используем интеграл
который сходится.
1
dx
,
2
x
11
12.
По предельному признаку сравнения2
x2 2 1
1
1
x
lim ln 2
:
lim
:
lim 2
1 0
2
2
2
x
x x 1 x
x x 1
x 1 x
интегралы
x2 2
1 ln x 2 1 dx и
одинаково, т.е. оба сходятся.
1
dx
ведут себя
2
x
Замечание. При вычислении предела вновь
воспользовались эквивалентностью функций
x2 2
ln 2
x
1
1
( x ).
2
x 1
12
13.
§2. Несобственный интеграл II рода (интеграл отразрывной функции)
Пусть f(x) непрерывна на промежутке [a, b) и имеет
бесконечный разрыв при x = b. Если существует
конечный предел
то его называют
несобственным интегралом второго рода и
обозначают
Таким образом, по определению
13
14.
Если предел в правой части существует, тонесобственный интеграл сходится. Если же указанный
предел не существует или равен бесконечности, то
говорят, что интеграл расходится.
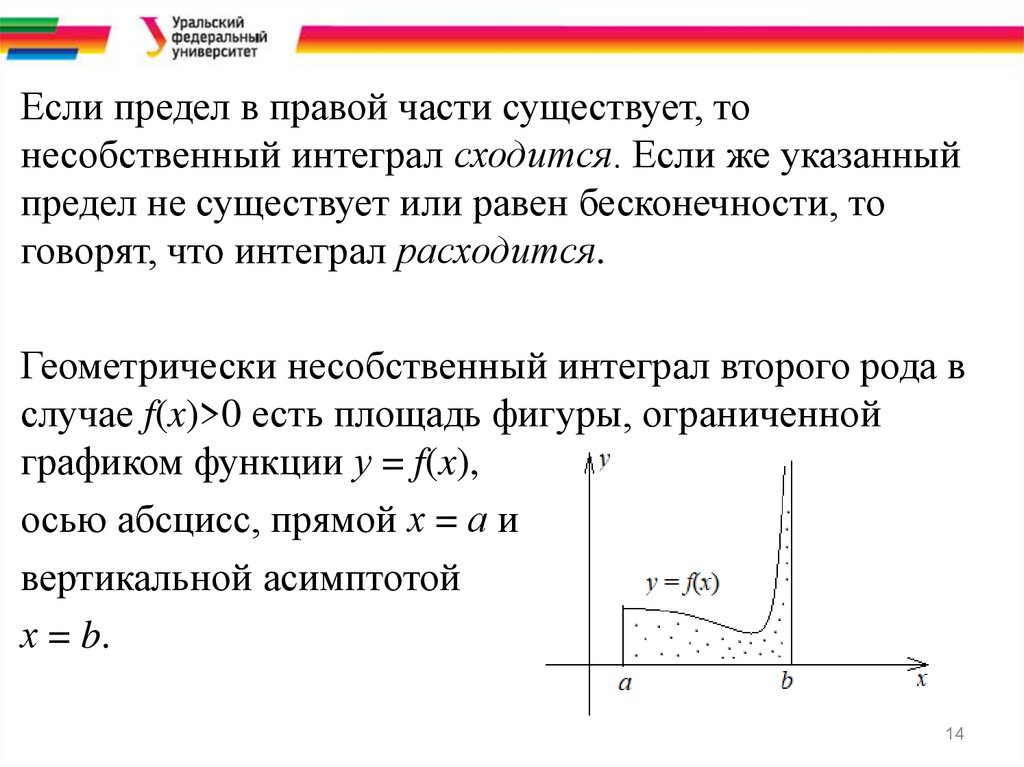
Геометрически несобственный интеграл второго рода в
случае f(x)>0 есть площадь фигуры, ограниченной
графиком функции у = f(x),
осью абсцисс, прямой х = а и
вертикальной асимптотой
х = b.
14
15.
Аналогично определяется несобственный интеграл вслучае, когда f(x) терпит бесконечный разрыв в точке
х = а:
Если функция f(x) терпит бесконечный разрыв во
внутренней точке с отрезка [a, b], то несобственный
интеграл второго рода определяется формулой:
В этом случае интеграл слева сходится, если сходятся
оба несобственных интеграла справа.
15
16.
1dx
Пример 4. Вычислить 2 .
x
1
Решение.
Подынтегральная функция терпит разрыв в точке с = 0
(точка разрыва 2-го рода).
1
0
1
dx
dx
dx
Поэтому, по определению 2 2 2 .
x
x
x
1
1
0
Вычислим первый интеграл
dx
dx
1
1
lim 2 lim
lim 1 .
1 x 2
0
0 x
0
x
1
1
0
1
dx
Следовательно, интеграл 2 расходится.
x
1
16
17.
Замечание. Если вычислять данный интеграл, необращая внимание на разрыв подынтегральной
функции в точке х = 0, то получим неверный результат
dx 1
1 x 2 x 1 1 1 2.
1
1
17
18.
Признаки сходимости несобственных интегралов IIрода аналогичны признакам сходимости
несобственных интегралов I рода.
В качестве интеграла, с которым производится
сравнение, используются интегралы вида:
которые сходятся при α < 1 и расходятся при α ≥ 1.
18
19.
12 x2 x
Пример 5. Исследовать на сходимость
dx.
sin x x
0
Решение.
Подынтегральная функция не определена в точке х = 0.
Выясним характер разрыва функции в этой точке:
2 x 2 x 0 ПЛ
(2 x 5 2 ) '
5 x3 2
0 ПЛ
lim
lim
lim
x 0 sin x x
0 x 0 (sin x x) ' x 0 cos x 1 0
15 x1 2
15 x 1 2
0 ПЛ
lim
lim
.
x 0 2( sin x )
0 x 0 4( cos x)
Следовательно, х = 0 точка разрыва второго рода
(бесконечный разрыв).
19
20.
Для сравнения возьмем интеграл видаa 0
dx
b 1
a ( x a)
1
b
1
dx ,
x1 2 который сходится.
2 0
По предельному признаку сравнения
2x2 x 1
2 x3
6x2
0 ПЛ
0 ПЛ
lim
:
lim
lim
x 0 sin x x x1 2
x 0 sin x x
x
0
cos x 1 0
0
12 x
lim
12 0,
x 0 sin x
поэтому оба интеграла ведут себя одинаково, т.е.
сходятся.
20


















 Математика
Математика








