Похожие презентации:
Декартова система координат в пространстве
1.
Декартова системакоординат в пространстве
2.
Определение• Упорядоченная система трёх
пересекающихся перпендикулярных друг
другу осей с общим началом отсчёта
(началом координат) и общей единицей
длины называется прямоугольной
декартовой системой координат в
пространстве.
3.
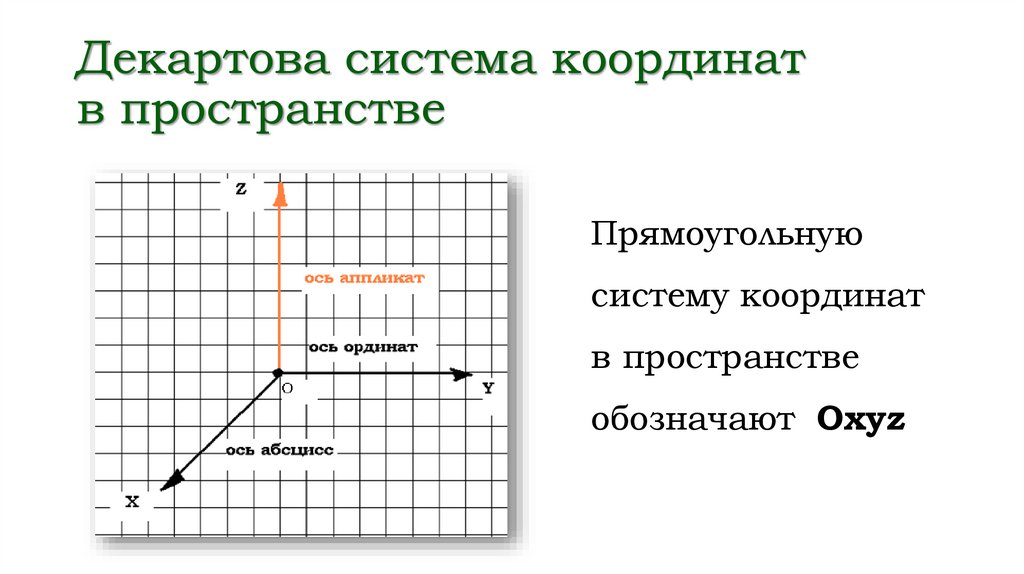
Декартова система координатв пространстве
Прямоугольную
систему координат
в пространстве
обозначают Охуz
4.
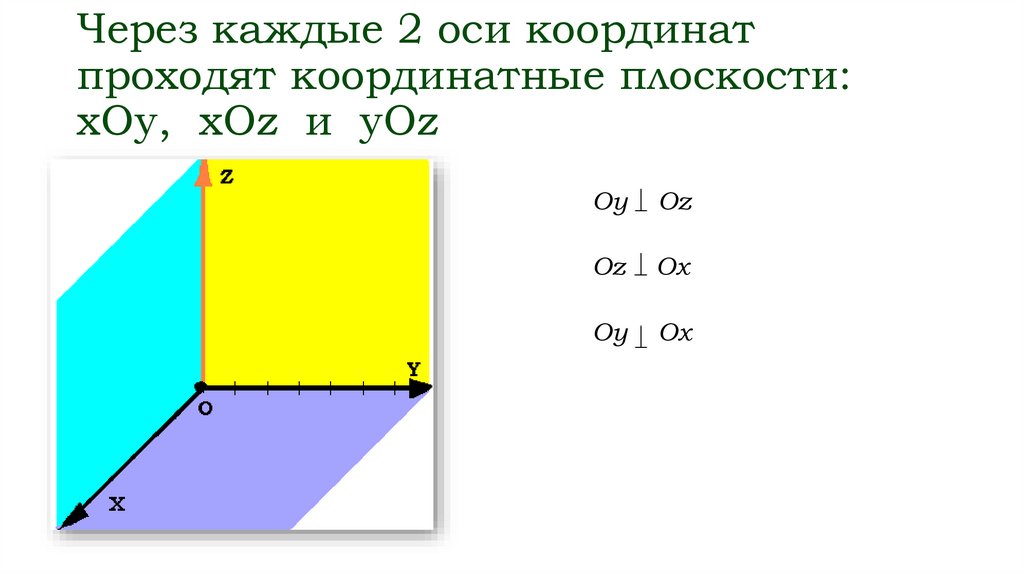
Через каждые 2 оси координатпроходят координатные плоскости:
xOy, xOz и yOz
Оy
Оz
Оz
Оx
Оy
Оx
5.
положительнаяполуось
Каждая ось делится точкой О на два
луча.
положительная
О
отрицательная
полуось
отрицательная
полуось
полуось
• В соответствии с этим,
лучи, направление
которых совпадает с
направлением оси,
называют
положительными
полуосями, а
оставшиеся лучи —
отрицательными
полуосями
6.
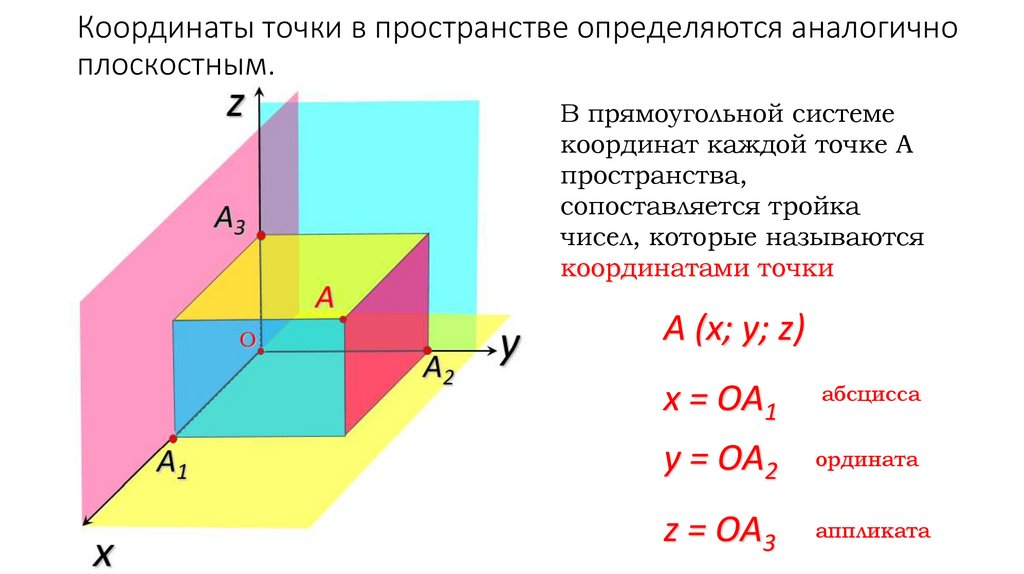
Координаты точки в пространстве определяются аналогичноплоскостным.
В прямоугольной системе
координат каждой точке А
пространства,
сопоставляется тройка
чисел, которые называются
координатами точки
А (x; y; z)
x = OА1
абсцисса
y = OА2
ордината
z = OА3
аппликата
7.
Декартова система координатна плоскости
• Частным случаем является система координат на плоскости,
например координатная плоскость xОу.
8.
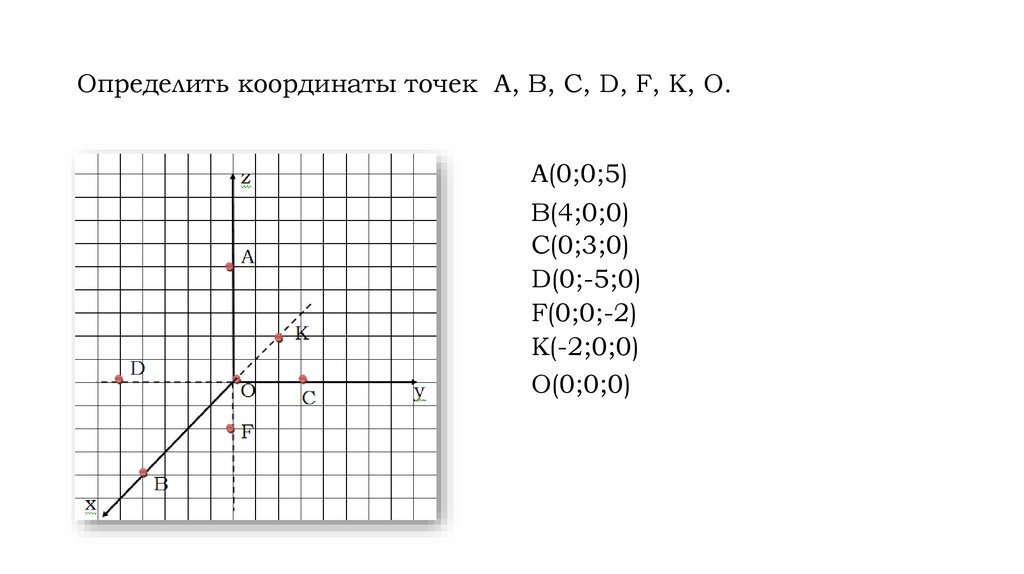
Определить координаты точек А, В, С, D, F, К, О.А(0;0;5)
В(4;0;0)
С(0;3;0)
D(0;-5;0)
F(0;0;-2)
К(-2;0;0)
О(0;0;0)
9.
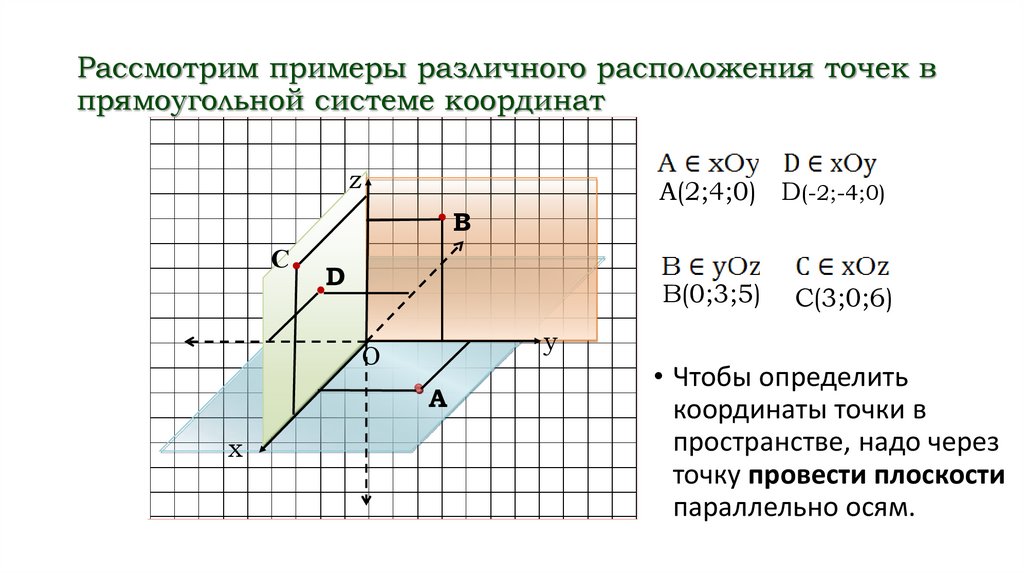
Рассмотрим примеры различного расположения точек впрямоугольной системе координат
z
А(2;4;0) D(-2;-4;0)
В
С
D
В(0;3;5)
y
О
А
x
С(3;0;6)
• Чтобы определить
координаты точки в
пространстве, надо через
точку провести плоскости
параллельно осям.
10.
точка лежитна оси
Ox (x; 0; 0)
Oy (0; y; 0)
Oz (0; 0; z)
в координатной
плоскости
Oyz (0; y; z)
Oxz (x; 0; z)
Oxz (x; 0; z)
11.
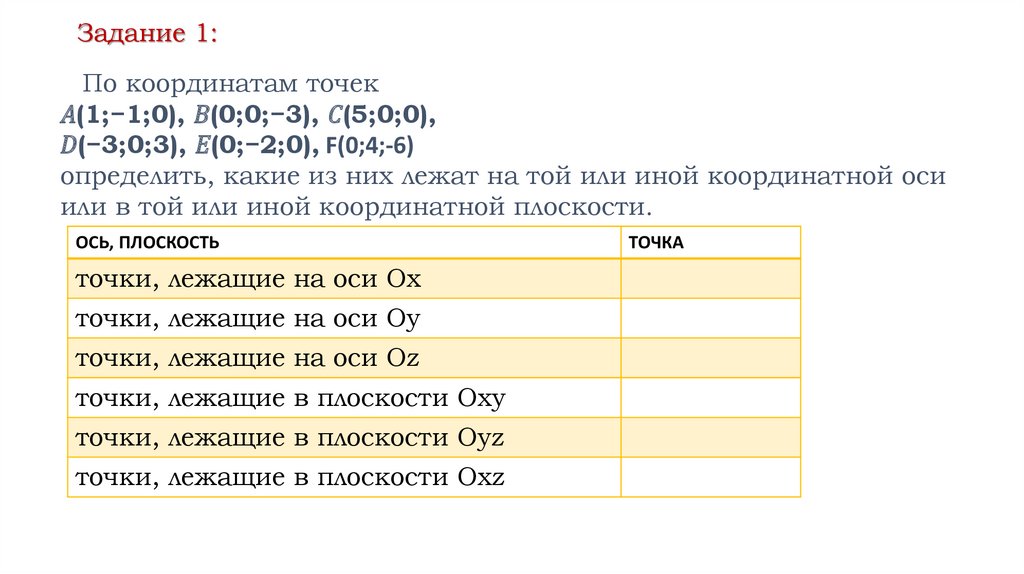
Задание 1:По координатам точек





 Математика
Математика








