Похожие презентации:
Линейная функция, её график и свойства
1.
*Повторение
1. Что называется функцией прямой
пропорциональности и какой формулой
она задается? Приведите пример
2.
* Ответ: Определение. Прямойпропорциональностью
называется функция, которую
можно задать формулой у=кх, где
х – независимая переменная, а k –
некоторое число, неравное нулю.
3.
*2. что такое угловойкоэффициент? Как влияет
его знак на расположение
графика прямой
пропорциональности
4.
*ответ : k- заданное постоянное число
Если k>0, то прямая расположена в Iи III
координатных четвертях
Если k<0, то прямая расположена в IIи IV
координатных четвертях
Если k=0, то прямая у=0 совпадает с осью Ох
5.
6.
• Функция вида у = kx + bназывается линейной.
• Графиком функции вида у = kx +b
является прямая.
• Для построения прямой
необходимы только две точки,
так как через две точки проходит
единственная прямая.
7.
8.
y = kx + b – линейная функциях – аргумент (независимая
переменная)
у – функция (зависимая
переменная)
k, b – числа (коэффициенты)
к≠0
9.
ху
Х1
Х2
Х3
У1
У2
У3
10.
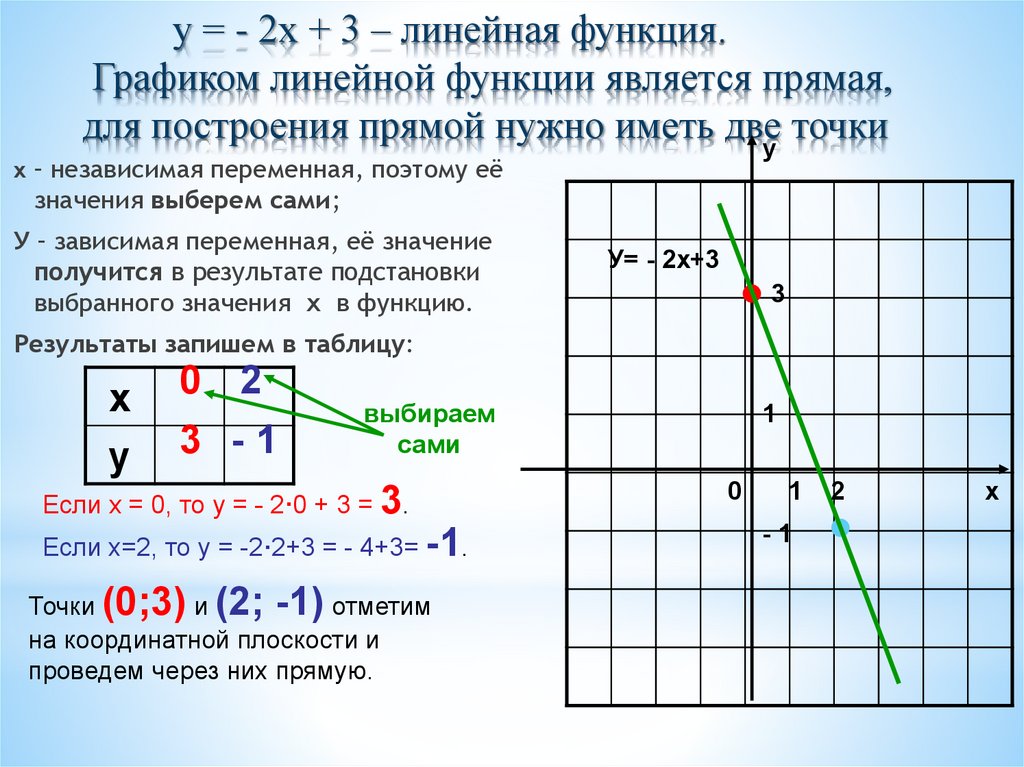
у = - 2х + 3 – линейная функция.Графиком линейной функции является прямая,
для построения прямой нужно иметь двеу точки
х – независимая переменная, поэтому её
значения выберем сами;
У – зависимая переменная, её значение
получится в результате подстановки
выбранного значения х в функцию.
У= - 2х+3
3
Результаты запишем в таблицу:
х
у
0 2
3 -1
выбираем
сами
Если х = 0, то у = - 2·0 + 3 = 3.
Если х=2, то у = -2·2+3 = - 4+3= -1.
Точки (0;3) и (2; -1) отметим
на координатной плоскости и
проведем через них прямую.
1
0
1
-1
2
х
11.
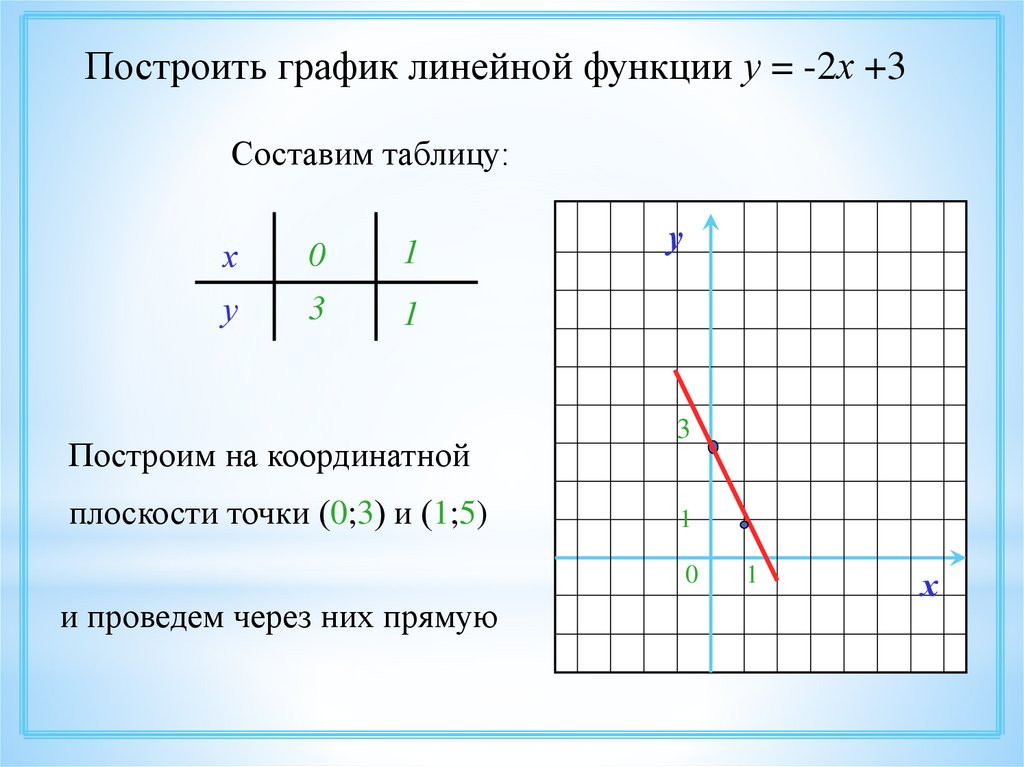
Построить график линейной функции у = -2х +3Составим таблицу:
х
0
1
у
3
1
Построим на координатной
плоскости точки (0;3) и (1;5)
у
3
1
0
и проведем через них прямую
1
х
12.
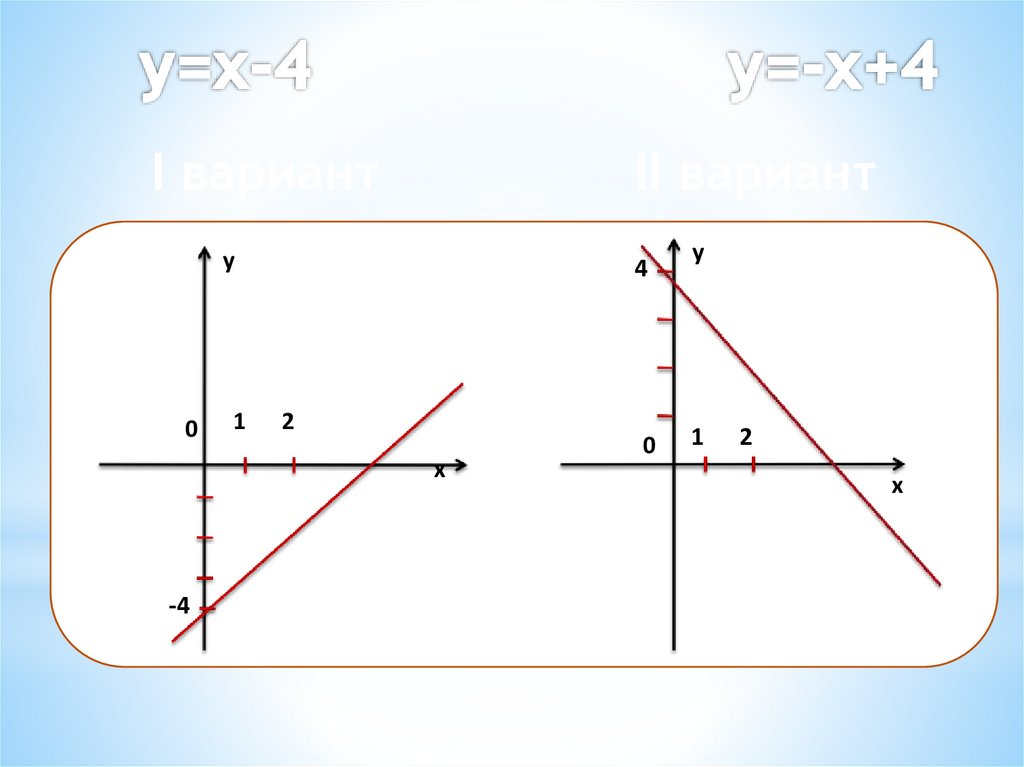
Построить график линейнойфункции
I вариант
II вариант
y=x-4
y=-x+4
13.
I вариантII вариант
y
0
1
4
2
x
-4
0
y
1
2
x
14.
15.
Мы узнали:*Функция вида у = kx + b называется линейной.
*Графиком функции вида у = kx + b является
прямая.
*Для построения прямой необходимы только две
точки, так как через две точки проходит
единственная прямая.
Выводы записать в тетрадь













 Математика
Математика








