Взаимное расположение прямых в пространстве. Угол между прямыми

1.

Тема: «Взаимное расположение прямых в
пространстве. Угол между прямыми.»
Выполнила: Уханева А.А.
Группа СД 14-05

2.

Скрещивающиеся прямые
Определение
Две прямые называются
скрещивающимися , если они не лежат в
одной плоскости.
a
b

3.

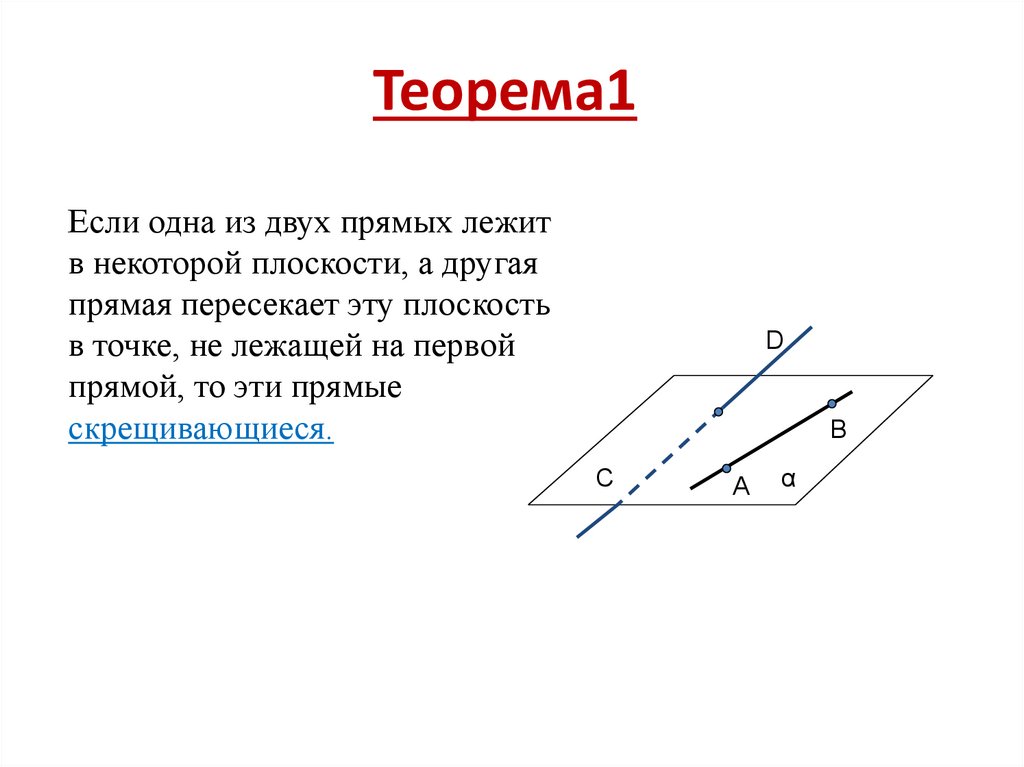
Теорема1
Если одна из двух прямых лежит
в некоторой плоскости, а другая
прямая пересекает эту плоскость
в точке, не лежащей на первой
прямой, то эти прямые
скрещивающиеся.
D
B
C
A
α

4.

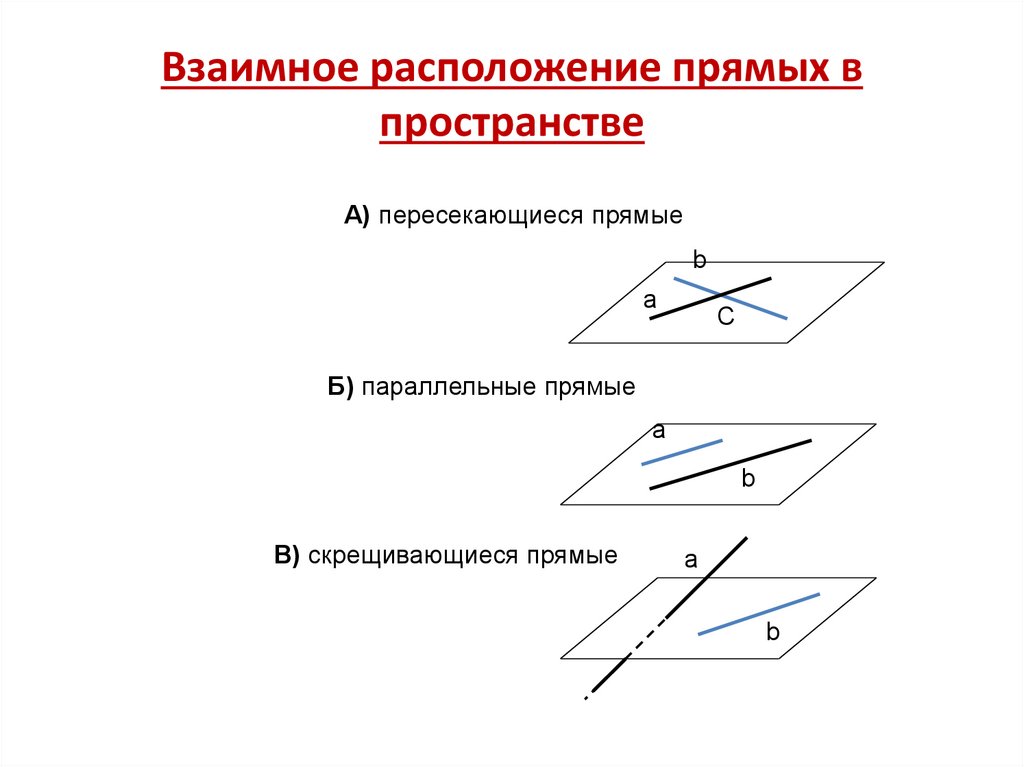
Взаимное расположение прямых в
пространстве
А) пересекающиеся прямые
b
a
C
Б) параллельные прямые
a
b
В) скрещивающиеся прямые
a
b

5.

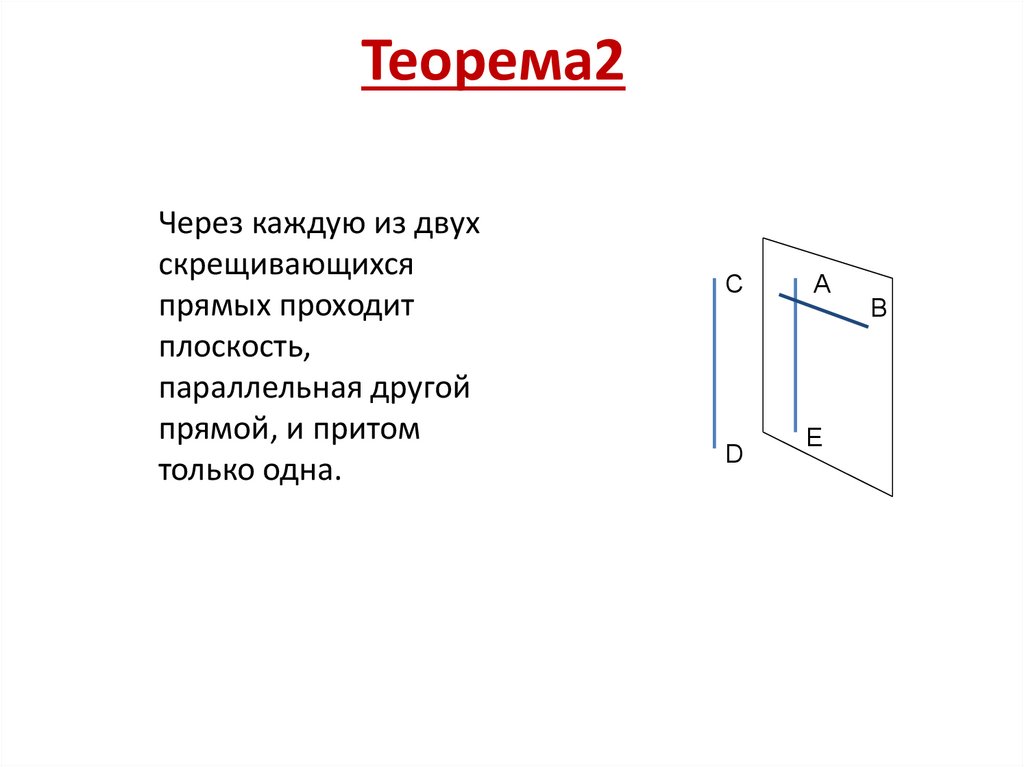
Теорема2
Через каждую из двух
скрещивающихся
прямых проходит
плоскость,
параллельная другой
прямой, и притом
только одна.
C
A
B
D
E

6.

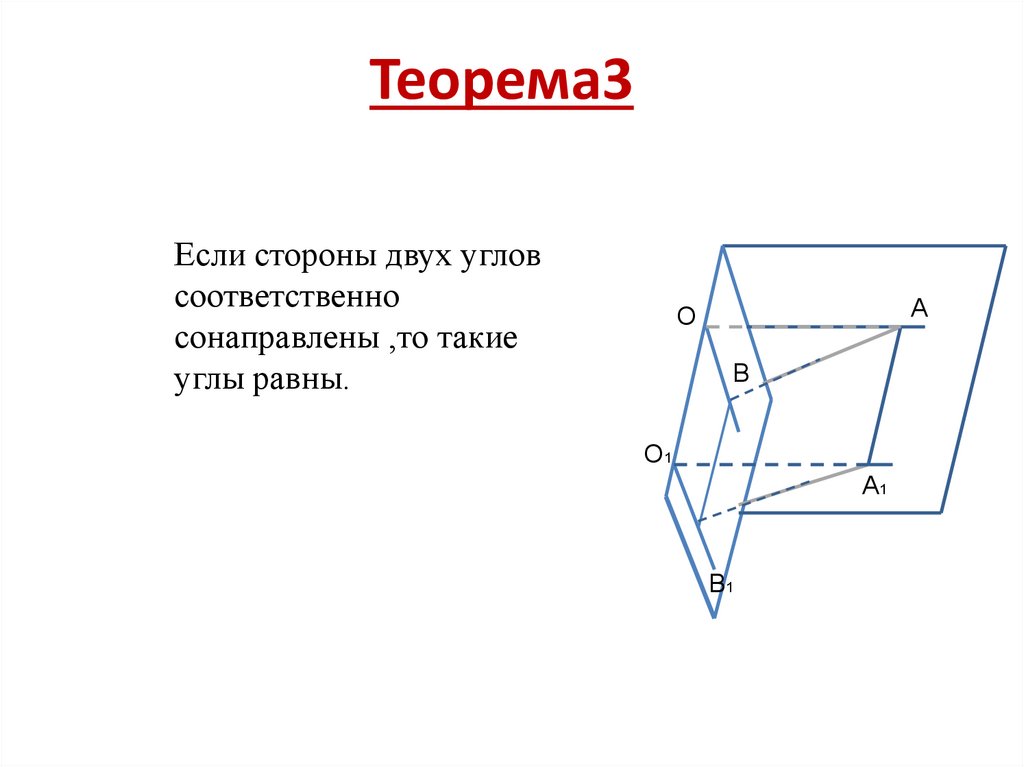
Теорема3
Если стороны двух углов
соответственно
сонаправлены ,то такие
углы равны.
A
O
B
O1
A1
B1

7.

Угол между двумя прямыми
Любые две пересекающиеся прямые лежат в одной
плоскости и образуют четыре неразвернутых угла.
Если известен один из этих углов ,то можно найти и
другие три угла.
Пусть α –тот из углов, который не превосходит
любой из трех остальных углов.
Тогда говорят, что угол между пересекающимися
прямыми равен α.
α
180-α

8.

Угол между скрещивающимися прямыми
Если угол между прямыми A1B1 и
C1D1 равен φ, то будем говорить,
что угол между
скрещивающимися прямыми AB
и CD равен φ.
A1
C1
A2
φ
φ
М1
D1
C2
М2
B1
D2
B2