Похожие презентации:
Степенная функция. 9 класс
1.
2.
Эпиграф урока:«… руководить ходом
своих мыслей, начиная с
предметов простейших
и легко познаваемых, и
восходить мало-помалу,
как по ступеням до
познания наиболее
сложных…»
Р. Декарт
3.
Линейная функция (прямаяпропорциональность), график - прямая,
проходящая через начало координат
Свойства функции у х :
1. D(f) = (− ∞; + ∞);
2. возрастает на всей
области определения;
3. не ограничена ни снизу,
ни сверху;
4. нет ни наибольшего, ни
наименьшего значения;
5. функция непрерывна;
6. Е(f) = (− ∞; + ∞).
4.
Квадратичная функция, график – парабола,вершина которой лежит в начале координат и
которая направлена ветвями вверх
2
Свойства функции у х :
1. D(f) = (− ∞; + ∞);
2. убывает на луче (− ∞; 0],
возрастает на луче [0; + ∞)
3. ограничена снизу, не
ограничена сверху;
4. Унаим. = 0, Унаиб. - не
существует;
5. функция непрерывна;
6. Е(f) = [0; + ∞);
7. выпукла снизу.
5.
у х723
6.
Тема:«Функции у = хn (n Є N), их свойства и
графики».
Задача:
Научиться строить графики функции
у = хn (n Є N) и изучить их свойства».
7.
ОпределениеФункцию у = хn , где n = 1, 2, 3, 4,
5, …, называют степенной
функцией с натуральным
показателем.
8.
План исследования функций:1.
2.
3.
4.
5.
6.
7.
8.
Указать область определения функции.
Определить четность или нечетность
функции (или отметить, что она не
является ни четной, ни нечетной).
Определить промежутки возрастания
и убывания функции.
Определить ограниченность функции.
Указать наибольшее и наименьшее
значение функции.
Определить непрерывность функции.
Указать область значений функции.
Определить выпуклость функции.
9.
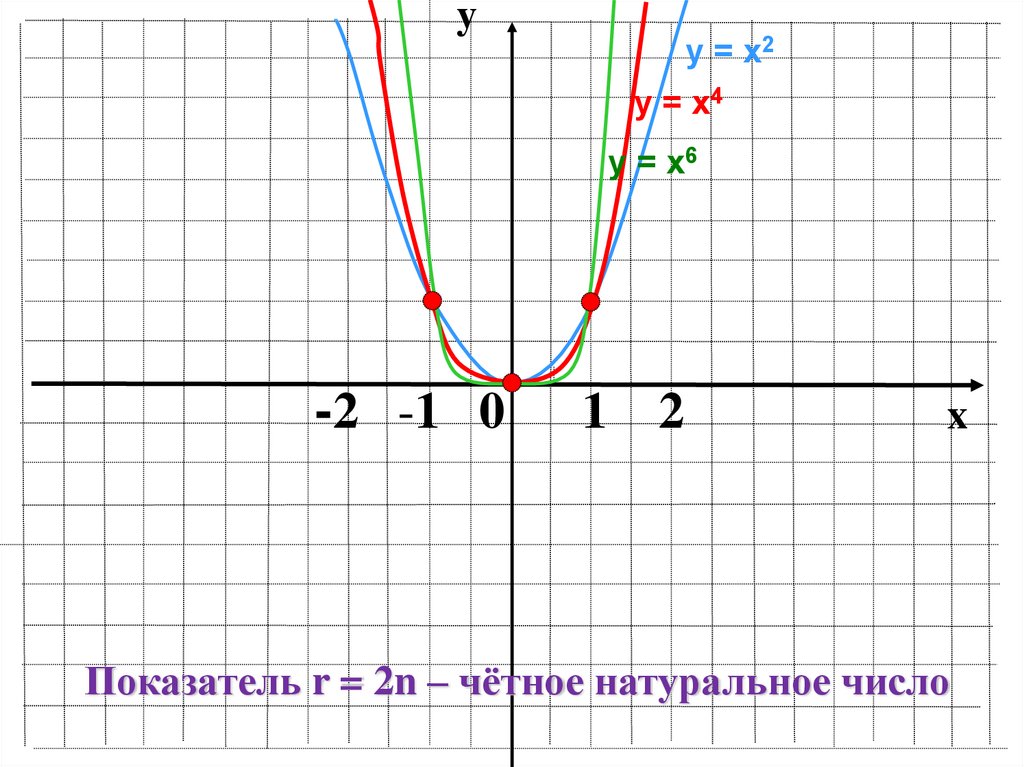
yу = х2
у = х4
у = х6
-2 -1 0
1
2
x
Показатель r = 2n – чётное натуральное число
10.
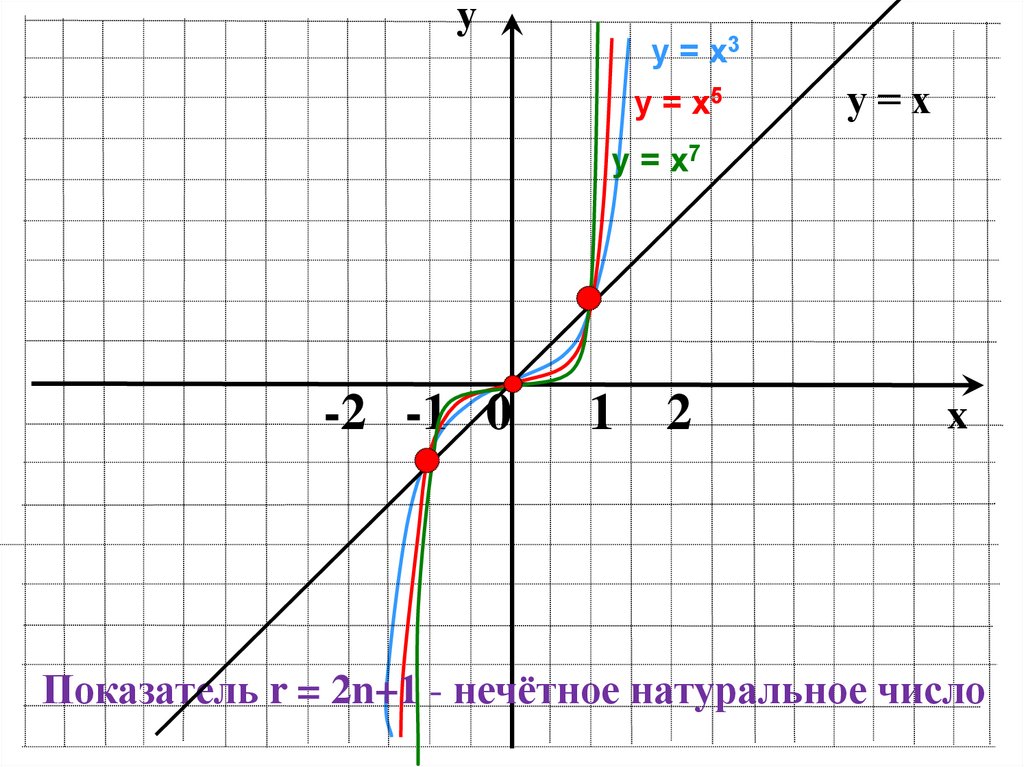
yу = х3
у = х5
у=х
у = х7
-2 -1 0
1 2
x
Показатель r = 2n+1 - нечётное натуральное число
11.
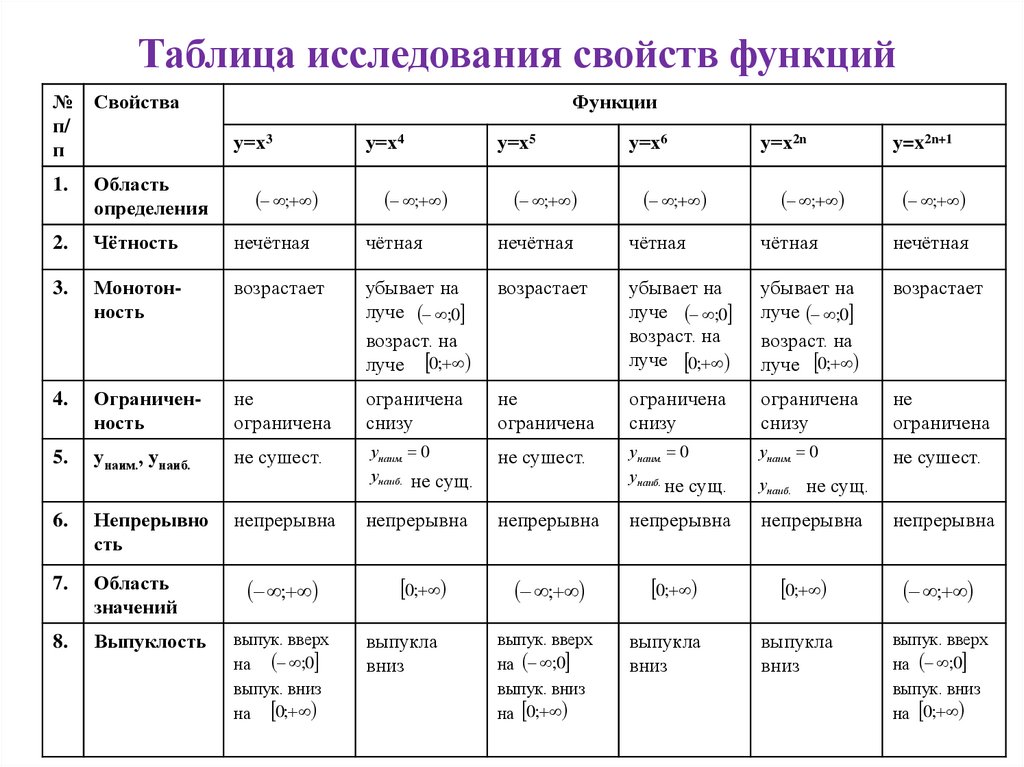
Таблица исследования свойств функций№
п/
п
Свойства
Функции
1.
Область
определения
2.
Чётность
нечётная
чётная
нечётная
чётная
чётная
нечётная
3.
Монотонность
возрастает
убывает на
луче ;0
возраст. на
луче 0;
возрастает
убывает на
луче ;0
возраст. на
луче 0;
убывает на
луче ;0
возраст. на
луче 0;
возрастает
4.
Ограниченность
не
ограничена
ограничена
снизу
не
ограничена
ограничена
снизу
ограничена
снизу
не
ограничена
5.
унаим., унаиб.
не сушест.
унаим. 0
не сушест.
унаим. 0
унаиб.
унаим. 0
не сушест.
непрерывна
непрерывна
непрерывна
;
0;
у=х3
6.
Непрерывно
сть
7.
Область
значений
8.
Выпуклость
;
непрерывна
;
выпук. вверх
на ;0
выпук. вниз
на 0;
у=х4
у=х5
;
унаиб.
;
не сущ.
непрерывна
0;
выпукла
вниз
у=х6
;
не сущ.
выпук. вверх
на ;0
выпук. вниз
на 0;
выпукла
вниз
у=х2n
;
у=x2n+1
;
унаиб. не сущ.
0;
выпукла
вниз
непрерывна
;
выпук. вверх
на ;0
выпук. вниз
на 0;
12.
Изменение графика степеннойфункции от значения показателя
http://fcior.edu.ru/card/7398/stepennaya-funkciyas-naturalnym-pokazatelem-ee-svoystva-i-grafiki1.html
http://fcior.edu.ru/card/6031/stepennaya-funkciyas-naturalnym-pokazatelem-ee-svoystva-i-grafikobratnaya-funkciya-ee-oblast-opred.html
(проверка усвоения материала 1-2 задания)
13.
КарточкаI вариант
II вариант
Выполняя моделирование, заполните пустые клетки таблицы:
Данная
функция
Новая
функция
Описание
преобразовани
я
Данная
функция
Новая функция Описание преобразования
Перенос на 2
y=x4
единицы вверх
y=x3
Перенос на 2 единицы вверх
y=x3
y=x3-4
y=x4
y=x4-4
y=x3
y=(x+1)3
y=x4
y=(x+1)4
y=x3
Перенос на 3
единицы
вправо
y=x4
Перенос на 3 единицы вправо
y=x3
Перенос на 1
единицу влево
и на 2
единицы вниз
y=x4
Перенос на 1 единицу влево и 2
единицы вниз
14.
Ответ на поставленный вопрос найден!Вывод:
График функции у х 723
и её свойства такие же как
2 n 1
у функции у х
.
15.
Домашнее задание:Пункт 4.1- 4.2
(свойства степенной функции с натуральным
показателем наизусть)
№210, 213(б), 218, 224, 228












 Математика
Математика