Деление отрезка в данном отношении

1. Деление отрезка в данном отношении

Даны две точки M 1 ( x1 , y1 , z1 ) и M 2 ( x 2 , y 2 , z 2 ) .
Найти координаты точки M3, делящей отрезок в
отношении , т.е. | M 1M 3 | или M1M 3 M 3 M 2
| M 3M 2 |
М2
M1M 3 ( x3 x1 , y3 y1 , z3 z1 )
M 3 M 2 ( x2 x3 , y2 y3 , z 2 z3 )
М3
М1
x3 x1 ( x 2 x3 ),
y3 y1 ( y 2 y3 ),
z 3 z1 ( z 2 z 3 ),
x1 x 2
x3 1 ,
y1 y 2
y3 1 ,
z1 z 2
z
.
3
1
1

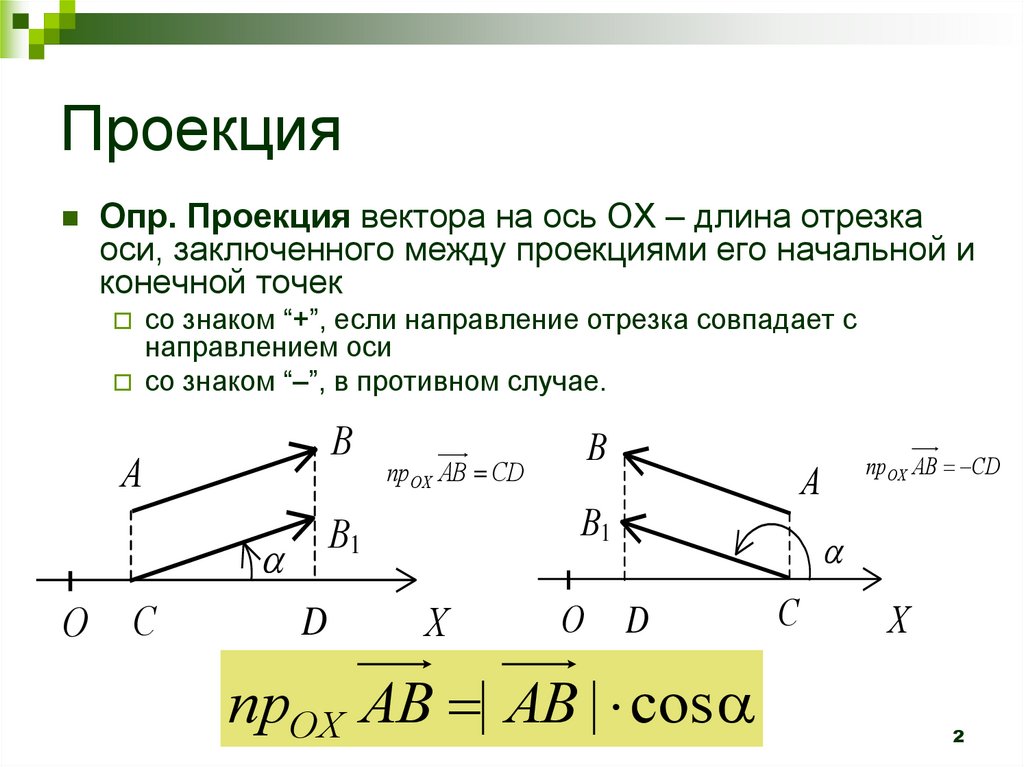
2. Проекция

Опр. Проекция вектора на ось ОХ – длина отрезка
оси, заключенного между проекциями его начальной и
конечной точек
со знаком “+”, если направление отрезка совпадает с
направлением оси
со знаком “–”, в противном случае.
В
А
О
С
пр OX AB CD
D
Х
О
пр OX AB CD
А
В1
В1
В
D
прOX AB | AB | cos
С
Х
2

3. Свойства проекции

1. пр е a пр е a
2. ï ðå (a b ) ï ðåa ï ðåb
3

4.

Теорема. Декартовы прямоугольные
координаты вектора равны проекциям
вектора a ( x, y, z ) на соответствующие оси
декартовой прямоугольной с/к.
x ï ðÎ Õ a
y ï ðÎ Y a
z ï ðÎ Z a
Из опр. проекции
x | a | cos
y | a | cos
z | a | cos
где , , – углы наклона вектора к осям OX, OY, OZ.
По т.Пифагора
| a | x 2 y 2 z 2
z
x
y
4

5. Направляющие косинусы

cos
x
x y z
2
cos
2
y
x y z
2
cos
2
2
2
2
2
z
x y z
2
2
2
2
cos cos cos 1
5

6. Скалярное произведение векторов

Ск. пр. – операция умножения вектора
на вектор, в результате которой
получается скаляр (число).
(a , b ) a b | a | | b | cos
(a, b ) | a | ï ðab | b | ï ðb a
6

7. Свойства

1. (a , b ) (b , a )
2. (a , b c ) (a , b ) (a , c )
3. (a , b ) (a , b ), где - константа
4. Если векторы a и b коллинеарны, то
(a , b ) | a | | b |
4а.
(a, a ) a | a |
2
2
7

8. Свойства

èëè b 0, òî (a , b ) 0
6. a b ( a , b ) 0
7. Åñëè (a , b ) 0, a 0, b 0,
5. a 0
8. (i , i ) i 1
( j, j) j 2 1
2
(k , k ) k 1
òî
a b
2
(i , j ) (i , k ) ( j , k ) 0
8

9. Скалярное произведение в координатной форме

Пусть
Тогда
a ( x1 , y1 , z1 ) x1i y1 j z1k
b ( x2 , y2 , z2 ) x2i y2 j z2k
(a , b ) ( x1i y1 j z1k , x2i y2 j z2k )
x1 x2 (i , i ) x1 y2 (i , j ) x1 z2 (i , k )
y1 x2 ( j , i ) y1 y2 ( j , j ) y1z2 ( j , k )
z1 x2 (k , i ) z1 y2 (k , j ) z1 z2 (k , k )
x1 x2 y1 y2 z1 z2 .
9

10.

( a , b ) x 1 x 2 y1 y 2 z 1 z 2
| a |
2
x1
2
y1
2
z1
(a , b )
cos
| a | | b |
(a , b )
ï ðb a
|b |
a b (a , b ) 0
10

11. Векторное произведение

Опр. Векторным произведением векторов a и b
называется вектор
c a b [a, b ] , который
1. c a и c b
2. | c | | a | | b | sin( a, b )
3. a, b , c - правая тройка
Правая
c
b
a
тройка.
Если смотреть с конца
вектора c , то кратчайший
поворот от a к b
происходит против
часовой стрелки.
11

12.

b
S h | a | | b | | a | sin
h
a
S a , b
12

13. Свойства

1. [a , b ] [b , a ]
2. [ a , b ] [a , b ]
3. [a b , c ] [a, c ] [b , c ]
Критерий коллинеарности
Если a 0 è b 0 , то [a , b ] 0 a b
13

14. Векторное произведение в координатной форме

a x1i y1 j z1k
b x2 i y 2 j z 2 k
[a , b ] [ x1i y1 j z1k , x2i y2 j z2k ]
0
0
x1 x2 [i , i ] x1 y2 [ik
, j ] x1z2 [i , k ] y1x2[ j ,ki ] y1 y2[ j , j ]
y1 z2 [ j , k ] z1 x2 [k , i ] z1 y2 [k , j ] z1z2 [k , k ].
k
i
i
j
0
[a , b ] x 1
j
k
y1
z1
x2
y2
z2
14

15. Векторное произведение в координатной форме

a x1i y1 j z1k
b x2 i y 2 j z 2 k
i
[a , b ] x 1
j
k
y1
z1
x2
y2
z2
15

16. Смешанное произведение векторов

Опр. Смешанным
произведением трех
векторов a ,b ,c , называется число,
равное
(a ,b ,c ) ([ a ,b ], c )
Свойства
1. (a b) c a (b c)
2. (a , b , c ) (b , c , a ) (c , a , b )
(b , a , c ) (a , c , b ) (c , b , a )
16