Кинематика. Операции с векторами

1.

ФИЗИКА ч. I
МЕХАНИКА

2.

Физика изучает наиболее общие законы
формирования
и развития окружающей нас материи в ее
наиболее примитивных формах,
которые принято называть неживой
природой.
Поэтому можно утверждать, что физика
является фундаментом всех естественных
наук.

3.

4.

“Пусть будет стыдно тому, кто бездумно пользуется
чудесами науки и техники, смысля в них не более
того, что смыслит в ботанике корова, с
удовольствием щиплющая траву.”
(А. Эйнштейн, 1903 г.)

5.

МАТЕМАТИЧЕСКОЕ
ВВЕДЕНИЕ
Операции с векторами

6.

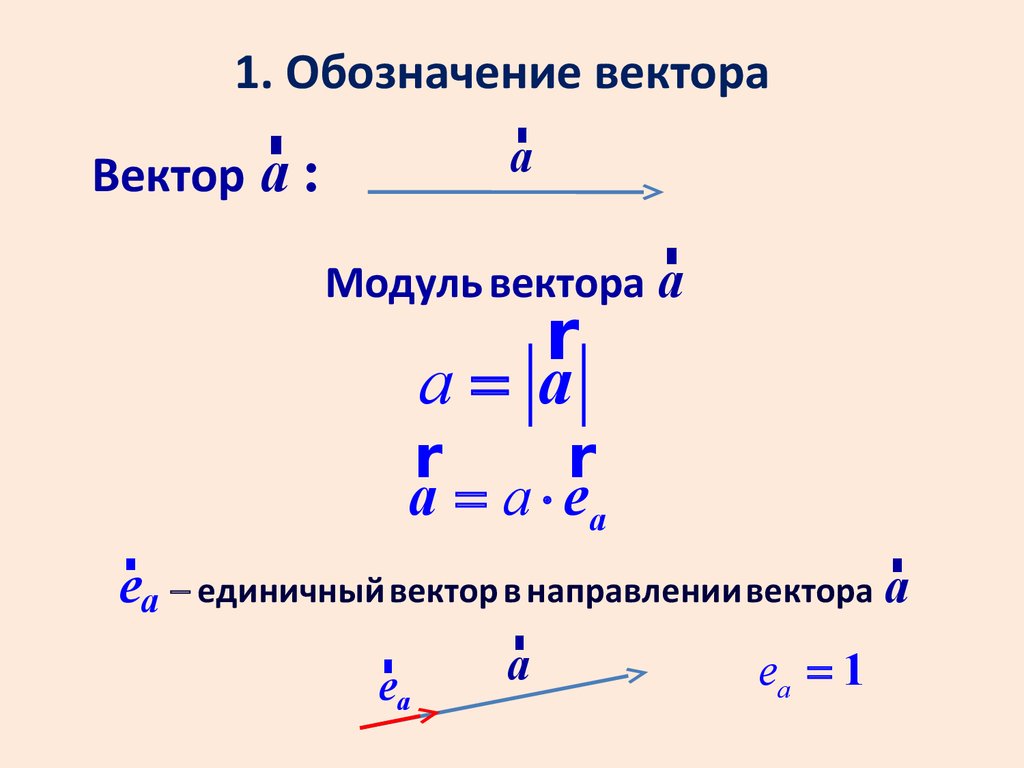
1. Обозначение вектора
r
a
r
Вектор a :
r
Модуль вектора a
r
a= a
r
r
a = a × ea
r
r
ea - единичный вектор в направлении вектора a
r
ea
r
a
ea = 1

7.

Орты
осей
координатных
r r r
Единичные векторы i , j и k ,
проведенные в направлении координатных осей,
называют ортами этих осей.
Такая тройка векторов полностью определяет
систему координат, поэтому ее называют
базисом координатной системы.

8.

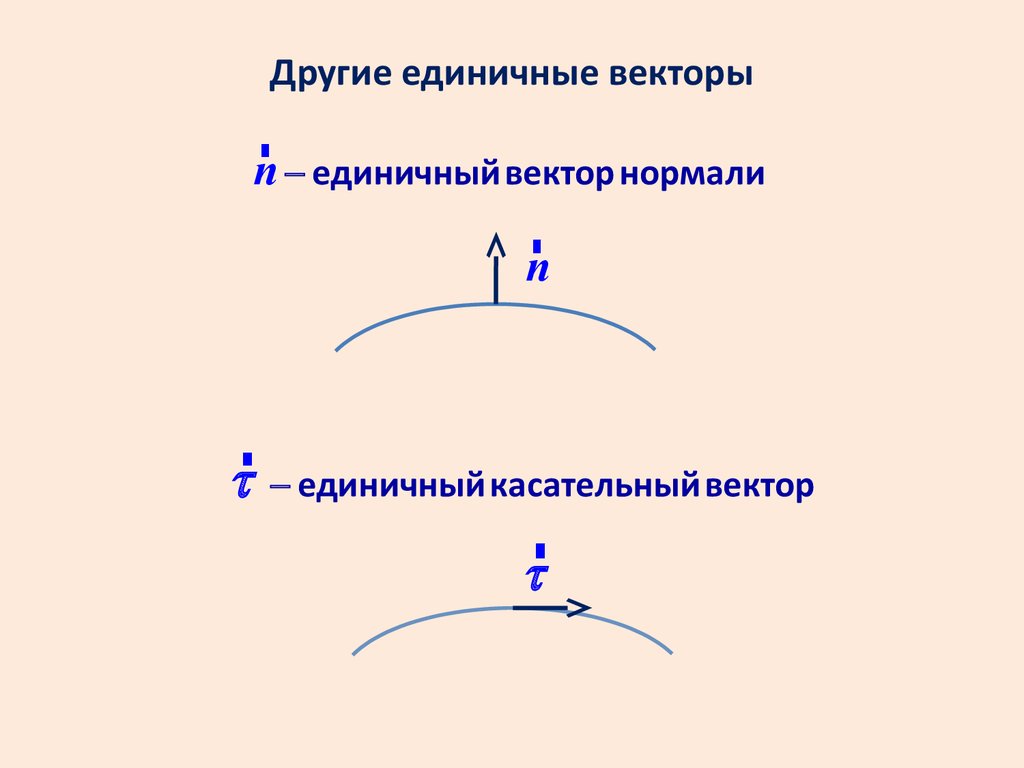
Другие единичные векторы
r
n - единичный вектор нормали
r
n
r
t - единичный касательный вектор
r
t

9.

2. Проекция вектора
a
x1
ах
x2
ax = x2 - x1
ax = a cos a
х

10.

3. Сложение векторов
r r r
с =a+b
a) правило параллелограмма
б) правило треугольника
и многоугольника

11.

4. Умножение вектора на число
r
a
r
b ( m > 0)
r
b ( m < 0)
По модулю
b= ma
r
r
b = ma

12.

5. Разложение вектора через проекции
y
ay
r
j
z
r
r i
k
r
a
ax
х
r
r
r
r
a = a x i + a y j + az k

13.

6. Скалярное произведение векторов
Обозначается
r r
c = (a , b )
или
r r
с = a ×b
Раскрывается
c = abcosa
r r
a - угол между а и b
r
а
a
r
b

14.

Примеры
c = abcos0 = ab
c = abcosp = - ab
p
c = abcos = 0
2
c = abb = aba
r r
r r
(a , b ) = (b , a )
r r
2
(a , a ) = a

15.

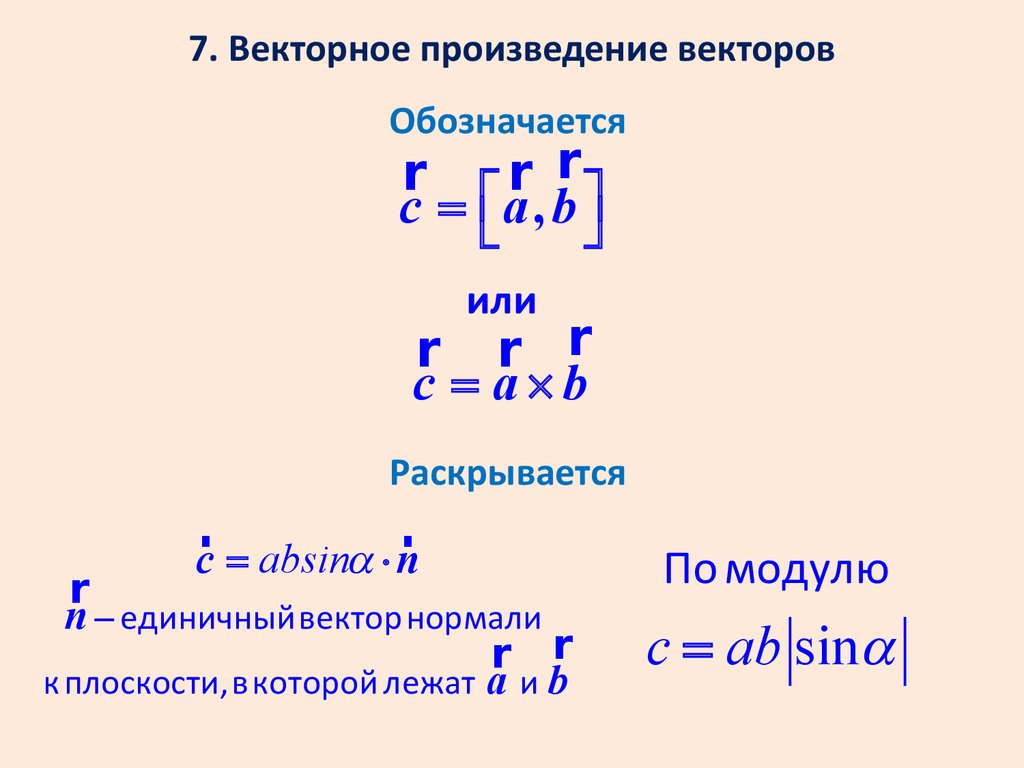
7. Векторное произведение векторов
Обозначается
r
r r
c = éë a , b ùû
или
r r r
с = a´b
Раскрывается
r
r
c = absina × n
r
n - единичный вектор нормали
r r
к плоскости, в которой лежат а и b
По модулю
c = ab sina

16.

r
Вектор c направлен по нормали к r
r
плоскости, в которой лежат векторы a и b.
Он перпендикулярен обоим
векторам-сомножителям.
r r r r
с ^a ис ^b

17.

r
c находят по
Направление вектора
правилу правого винта.
r
c
r
b
r
n
a
r
a
r
Если смотреть
вслед вектору c ,
r
r
то поворот от а к b осуществляется по часовой стрелке.
r r r
a, b и c образуют правую тройку векторов

18.

Примеры
c = absin0 = 0
c = absinp = 0
p
c = absin = ab
2
r r
r r
éa , b ù = - éb , a ù
ë
û
ë
û
r r
[ a, a] = 0

19.

8. Производная вектора
r
r
r
dea
da d ( a × ea ) da r
=
=
× ea + a ×
dt
dt
dt
dt
Показывает, как изменяется
модуль вектора.
Показывает, как изменяется
направление вектора.

20.

МЕХАНИКА

21.

Механика изучает движение тел.
Механическое движение –
изменение положения тела
относительно других тел.
Для описания движения
необходима система отсчёта: тело
отсчёта, система координат, часы.
21

22.

За тело отсчета принимают такое тело,
которое в данной задаче можно условно
считать неподвижным.
Тело отсчета

23.

Основная задача механики– зная положение и скорость
тела в начальный момент
времени, определить положение
и скорость тела в произвольный
момент времени.

24.

Реальные физические
явления очень сложны и, как
правило, возможно лишь
приближенное их описание.
Для этого пользуются
упрощающими моделями.

25.

Материальная точка –
– тело, размерами и формой
которого в данной задаче можно
пренебречь.
(Массой – нельзя!)
Абсолютно твердое тело –
– такое тело, деформацией которого
можно пренебречь.

26.

ВИДЫ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
Поступательное движение – все точки тела
движутся одинаково. Любая прямая, связанная
с телом, параллельна самой себе.
Достаточно описать движение одной точки.
Вращательное движение – точки тела движутся
по окружностям, центры которых лежат на
неподвижной прямой, называемой осью
вращения.

27.

Кинематика материальной точки
Траектория – линия, по которой
движется материальная точка.
Положение точки на траектории можно
задать либо с помощью координат х,r y,
z, либо с помощью радиус–вектора r .

28.

Радиус-вектор – это вектор, проведенный из
начала координат в данную точку траектории.
y
ае
тр
0
ия
ор
кт
r
r
x

29.

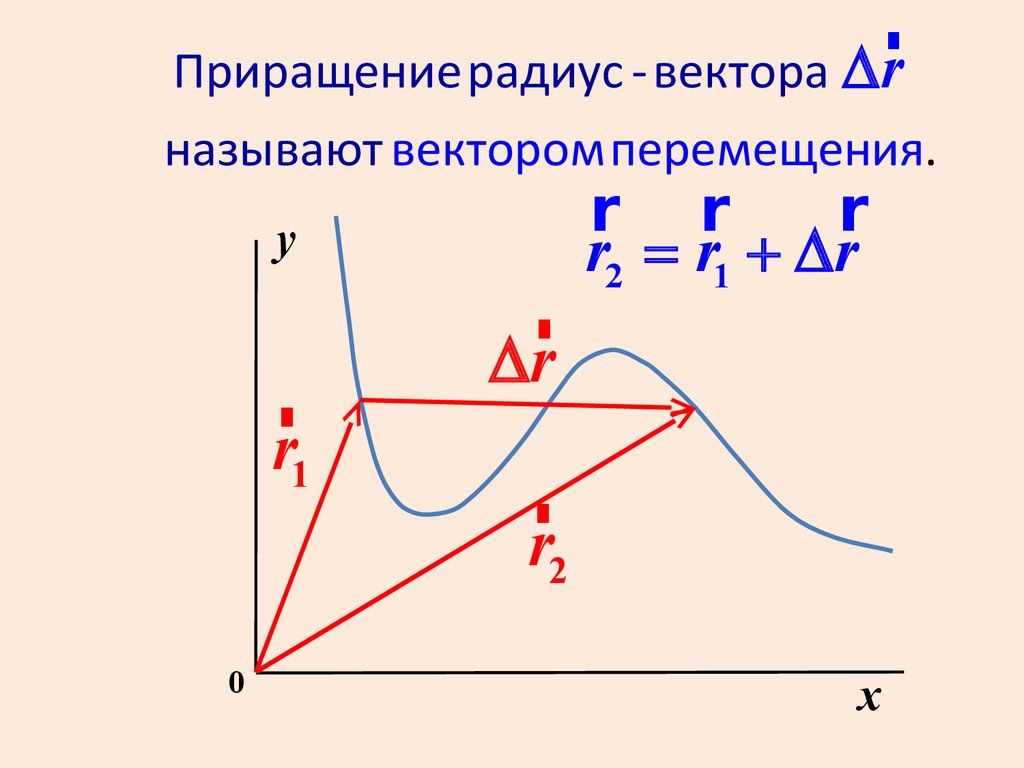
r
Приращение радиус - вектора Dr
называют вектором перемещения.
y
r
r1
0
r
Dr
r r
r
r2 = r1 + Dr
r
r2
x

30.

Длина участка траектории между
двумя положениями МТ - это путь Ds.
y
r
r1
0
r
Dr
Ds
[ Dsм] = [ ]
r
r2
x

31.

Путь и модуль вектора перемещения равны только
в случае однонаправленного прямолинейного
движения. Во всех других случаях путь больше.
r
Ds ³ Dr
Обе величины равны также при бесконечно
малом перемещении.
r
ds = dr

32.

СКОРОСТЬ
Скорость – это величина,
характеризующая быстроту
изменения радиус-вектора
материальной точки со временем.

33.

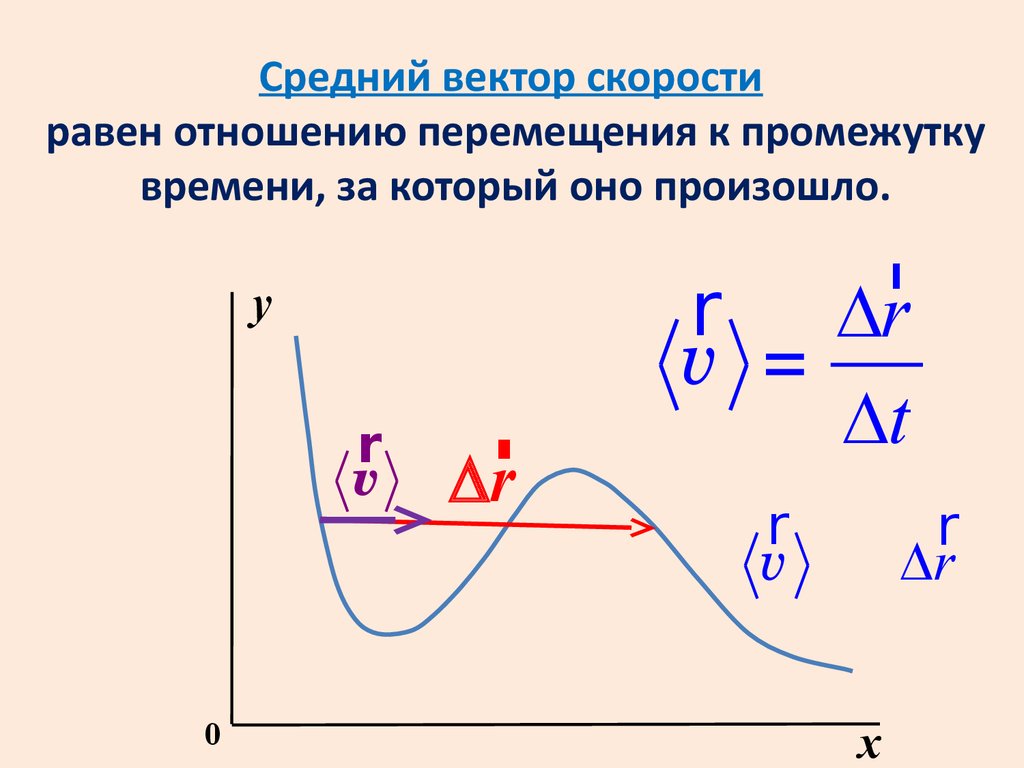
Средний вектор скорости
равен отношению перемещения к промежутку
времени, за который оно произошло.
y
r
v
0
r
Dr
r
r Dr
v =
Dt
r
r
v ­ ­ Dr
x

34.

Средняя путевая скорость
(средний модуль скорости) равна
отношению пути к промежутку времени,
за который этот путь пройден.
Ds
v =
Dt

35.

Если траектория замкнута, то
r
r
Dr = 0 и v = 0,
а Ds ¹ 0 и v ¹ 0.

36.

Мгновенная скорость – это скорость в
данный момент времени. Ее находят
как предел средней скорости при
Dt 0.
r
r
r
Δr
v = lim v = lim
Dt 0
Dt 0 Δt
r
r d r r&
v=
=r
dt

37.

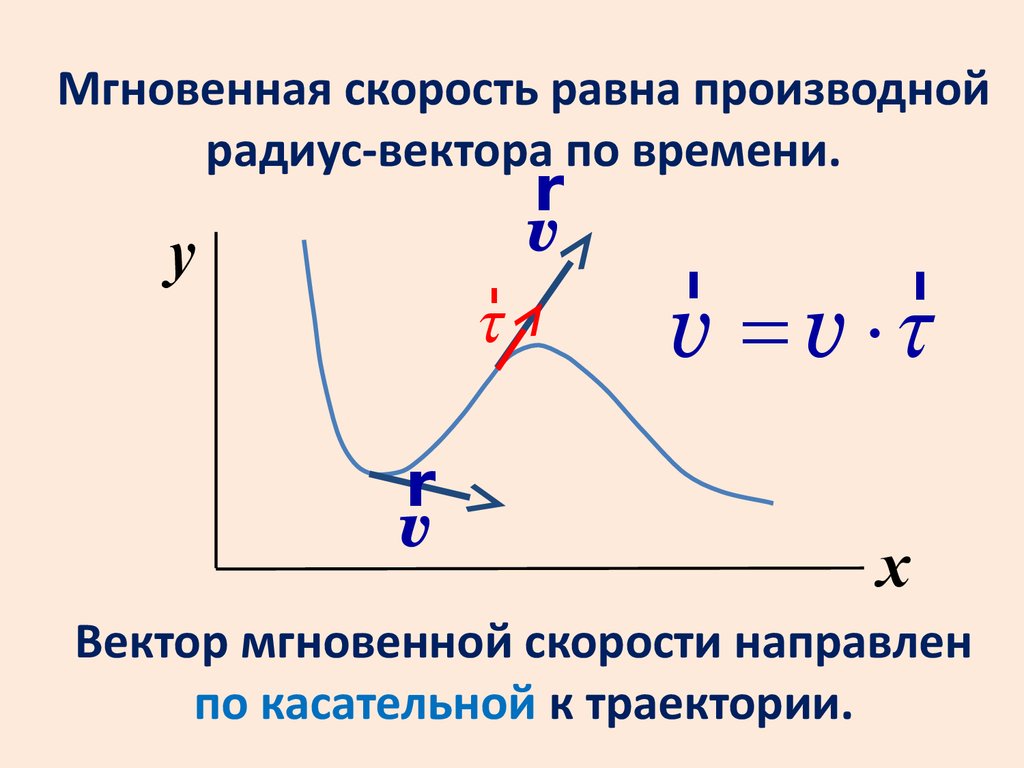
Мгновенная скорость равна производной
радиус-вектора по времени.
y
r
t
r
v
r
v
r
r
v = v ×t
x
Вектор мгновенной скорости направлен
по касательной к траектории.

38.

Модуль мгновенной скорости
находят как производную пути по времени.
r
r dr
v= v =
dt
r
dr = ds
ds
v = = s&
dt
é мù
[ v] = ê ú
ëсû

39.

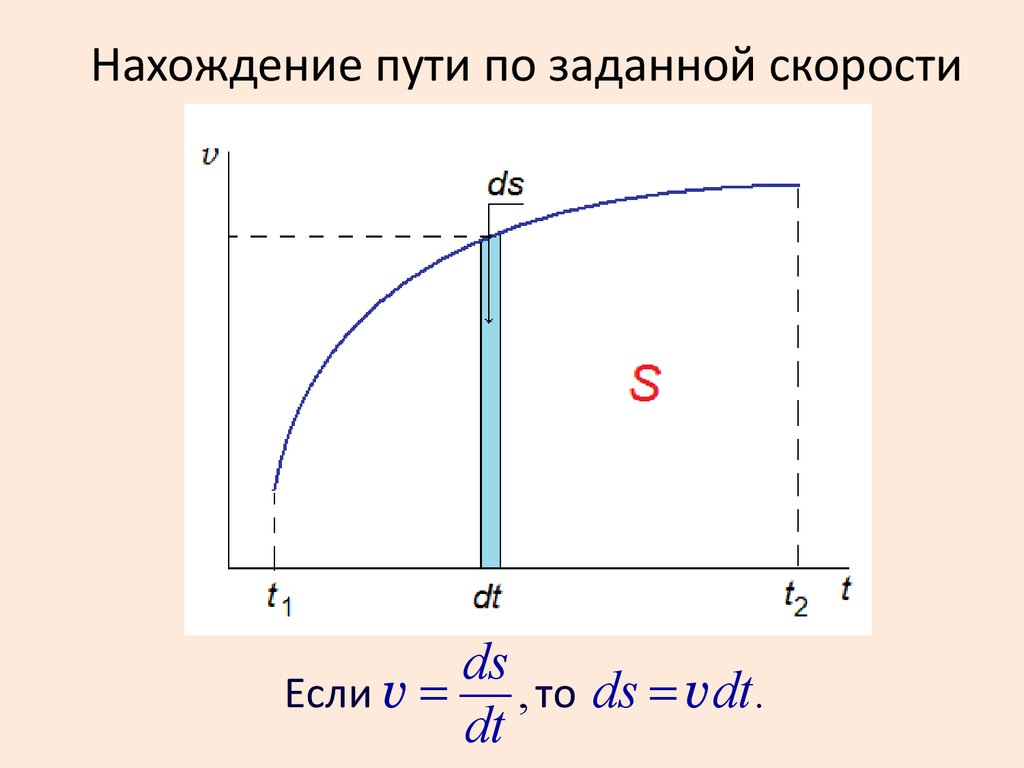
Нахождение пути по заданной скорости
ds
Если v =
, то ds = vdt.
dt

40.

Путь, пройденный за время от t1 до t2:
t2
Ds = ò vdt
t1
На графике это площадь под кривой v(t).
В случае v=const.:
t2
Ds = v ò dt = v(t2 - t1 )
t1