Похожие презентации:
Дифференциальное исчисление функций одной действительной переменной 11. Вычисление производных (продолжение)
1. Дифференциальное исчисление функций одной действительной переменной
11. Вычисление производных(продолжение).
Производные высших порядков
2. Правила дифференцирования
• u=u(x), v=v(x) – дифференцируемые на (a; b)функции, с – const
u v u v
u v u v u v
u u v u v
2
v
v
c u c u
u u
с
с
2
3. Правила дифференцирования
d (u v) du dvd (u v) v du u dv
u v du u dv
d
2
v
v
4. Таблица производных
c 0 x nxn
a a ln a
e e
x
x
1
log a x
x ln a
sin x cos x
1
tgx 2
cos x
1
arcsin x
1 x2
x 1 x 2 x
n 1
x
x
1
ln x
x
cos x sin x
1
ctgx 2
sin x
1
arctgx
1 x2
1
1
1
2
x
x
sh x ch x
ch x sh x
cth x
1
sh 2 x
arccos x
1
1 x2
1
arcctgx
1 x2
5. Производная сложной функции.
• Если функции y=f(u) и u=g(x) имеютпроизводные в точках u0=g(x0) и x0
соответственно, то сложная функция y=f(g(x))
имеет производную в точке x0, которая
находится по формуле: y x yu u x
6. Дифференциал сложной функции
• Пусть функции y=f(u) и u=g(x) –дифференцируемые функции, y=f(g(x)) – сложная
функция
y x yu u x
y x dx yu u x dx
du u x dx
dy yu du
dy y dx
dy y x dx
dx x
du u
Первый дифференциал сложной функции обладает
свойством инвариантности (неизменности) формы.
6
7. Производная обратной функции.
• Если функция y=f(x) строго монотонна наинтервале (a; b) и в произвольной точке х0
данного интервала имеет конечную отличную
от нуля производную (y/(х0)≠0), то обратная ей
функция x=f – 1(y)=φ(y) также имеет
производную х/ в соответствующей точке у0
(f(х0)= у0, φ(y0)= x0), причем
1
( y0 )
f ( x0 )
1
x y ( y )
y x ( x)
7
8.
1( y0 )
f ( x0 )
x ( y ) ( f ( x))
x ( f ( x))
1 y f x
1
y
f x
8
9. Логарифмическая производная
1ln f ( x) f ( x) f ( x)
f ( x) f ( x) ln f ( x)
x nx
n
n 1
f ( x) x ( x 0, R)
f ( x) ( x ) x (ln x ) x ( ln x)
1
x x 1
x
x x
1
9
10. Производная показательно-степенной функции
Производная показательностепенной функцииy u ( x)
v( x)
(u( x) 0)
ln y v( x) ln u ( x)
(ln y ) (v( x) ln u ( x) )
y
u ( x)
v ( x) ln u ( x) v( x)
y
u ( x)
u ( x)
v( x)
y u ( x) v ( x) ln u ( x) v( x)
u ( x)
ln y ln u( x)v ( x )
y u ln u v v u
v
v 1
u
10
11. Производная параметрически заданной функции
x (t ),y
t
(
a
;
b
)
x ?
y (t ),
t ( x)
1
y (t ) ( ( x))
1
1
y x t ( ) x t
t
1
yt
y x
xt
11
12. Производная неявно заданной функции
Пусть у=f(х) – дифференцируемая функция переменной х.F ( x; y ) 0
F ( x; f ( x)) 0
Дифференцируем по х обе части уравнения с учетом того,
что у – функция переменной х .
Fx ( x; y ) Fy ( x; y ) y x 0
Fx
y x
Fy
12
13. Производные высших порядков
y f (x) производная первого порядкадифференцируемая функция
( y ) y производная второго порядка
d y d dy dy
y xx , f ( x), y ,
,
,
2
dx
dx dx dx
( n 1)
( n)
(y
) y производная п-го порядка
2
( 2)
13
14. Производные высших порядков от параметрически заданной функции
ytx (t ),
t (a; b)
y x
xt
y (t ),
x (t ),
yt
y
y
(
t
)
x
x ) t xt t
(
y
y xx ( y x ) x ( y x ) t t x
xt
xt
yt xt xt yt
3
( xt )
14
15. Дифференциалы высших порядков
• Пусть y=f(х) – дифференцируемая функцияdy f ( x) dx
– дифференциал первого порядка
dy y dx
dx x h
d (dy ) d y d f – дифференциал второго порядка
2
2
d y d (dy ) d ( y h) ( y h) x y h x
2
d ( y ) h y d (h) ( y x) h y 0
d y y (dx) y dx
3
2
3
d y d (d y) y dx – дифференциал третьего порядка
2
d y d (d
n
2
2
n 1
(n)
y) y (dx) – дифференциал п-го порядка
n
15
16. Высшие дифференциалы не обладают свойством инвариантности формы
• y=f(g(x)) – сложная функция, u=g(x) – промежуточнаяdy yu du
d y d (dy ) d ( yu du )
2
d ( yu ) du yu d (du ) yu du du yu d (du)
yu du yu d u
2
d y y x dx
2
2
2
2
d y
y x
2
dx
16


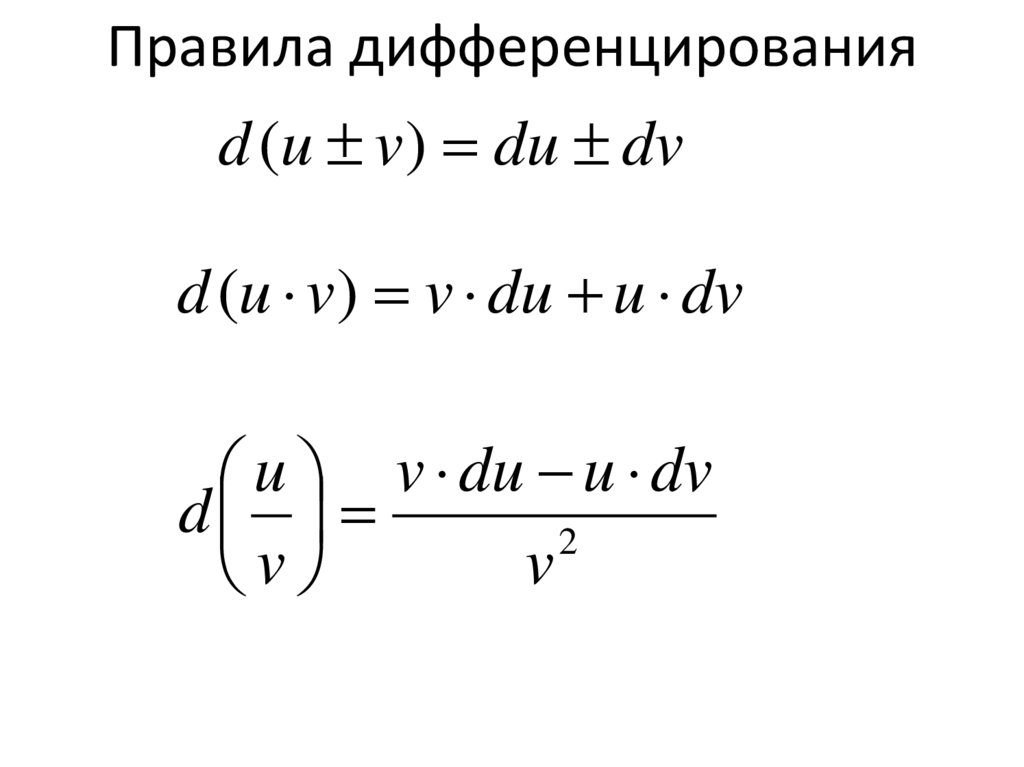




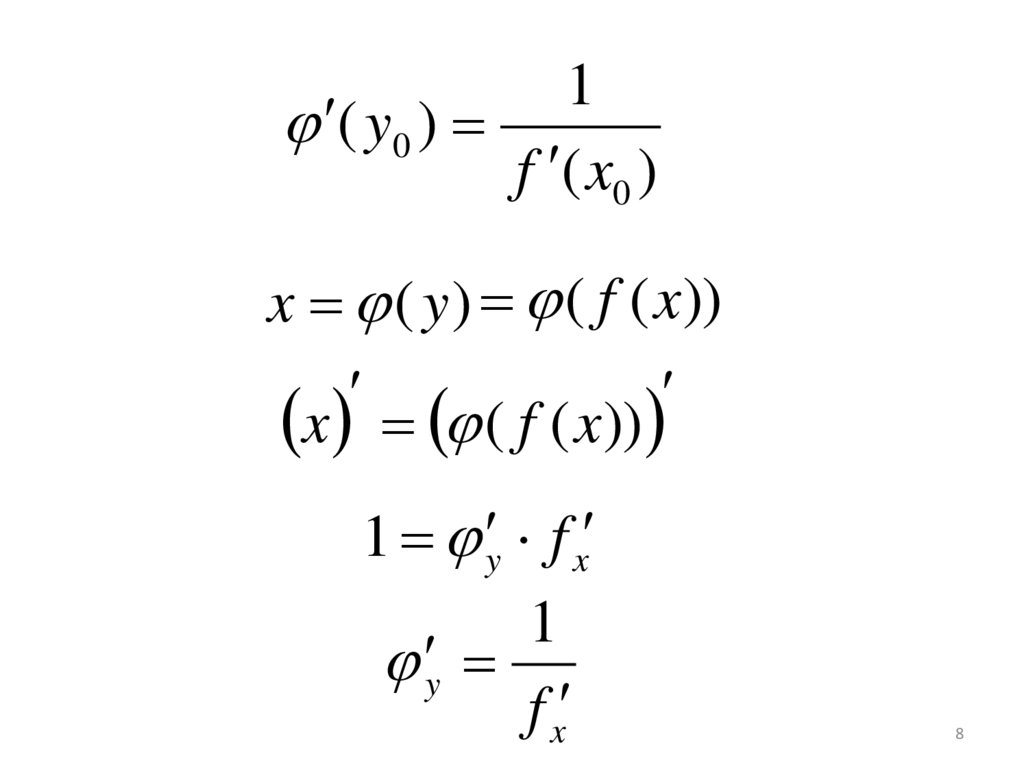
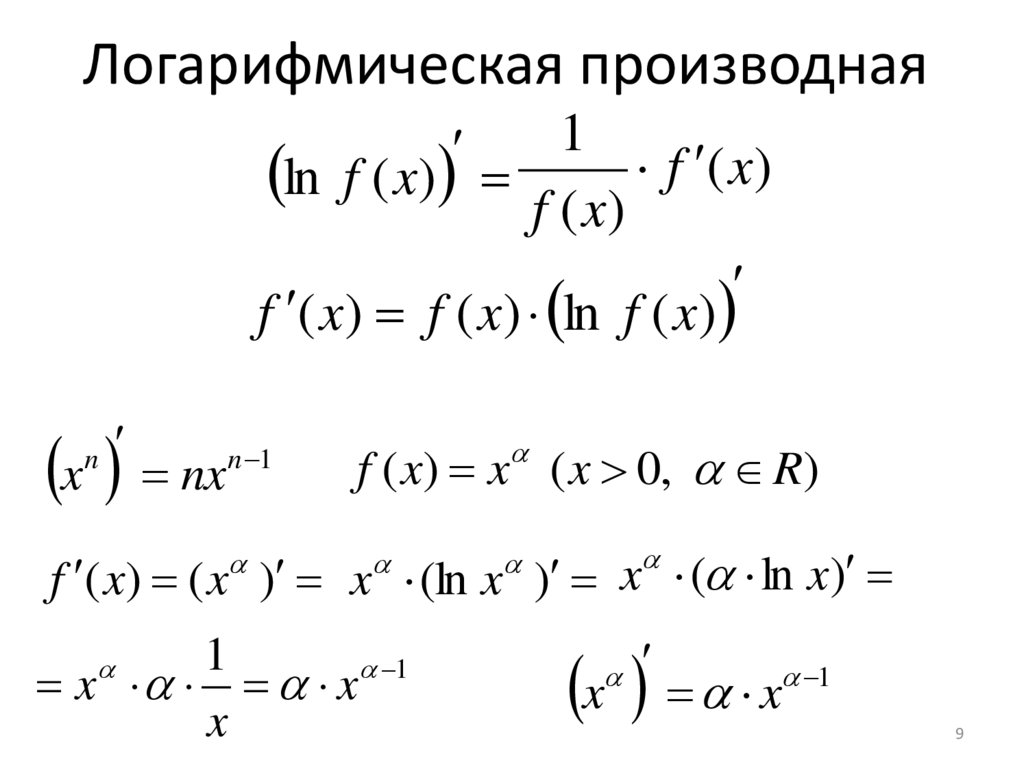







 Математика
Математика








