Похожие презентации:
Сумма углов треугольника
1.
2. Цели:
• сформулировать и доказатьтеорему о сумме углов
треугольника;
• рассмотреть задачи на
применение доказанной
теоремы.
3. Повторим изученное …
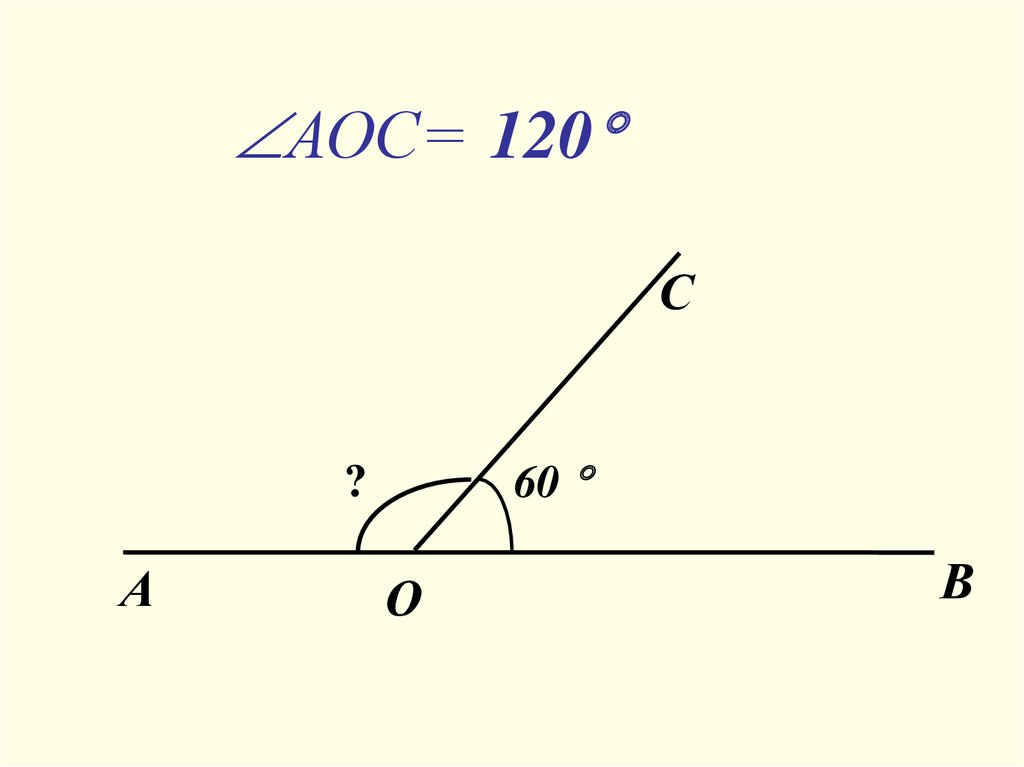
4.
АОС= 120С
60
?
А
О
В
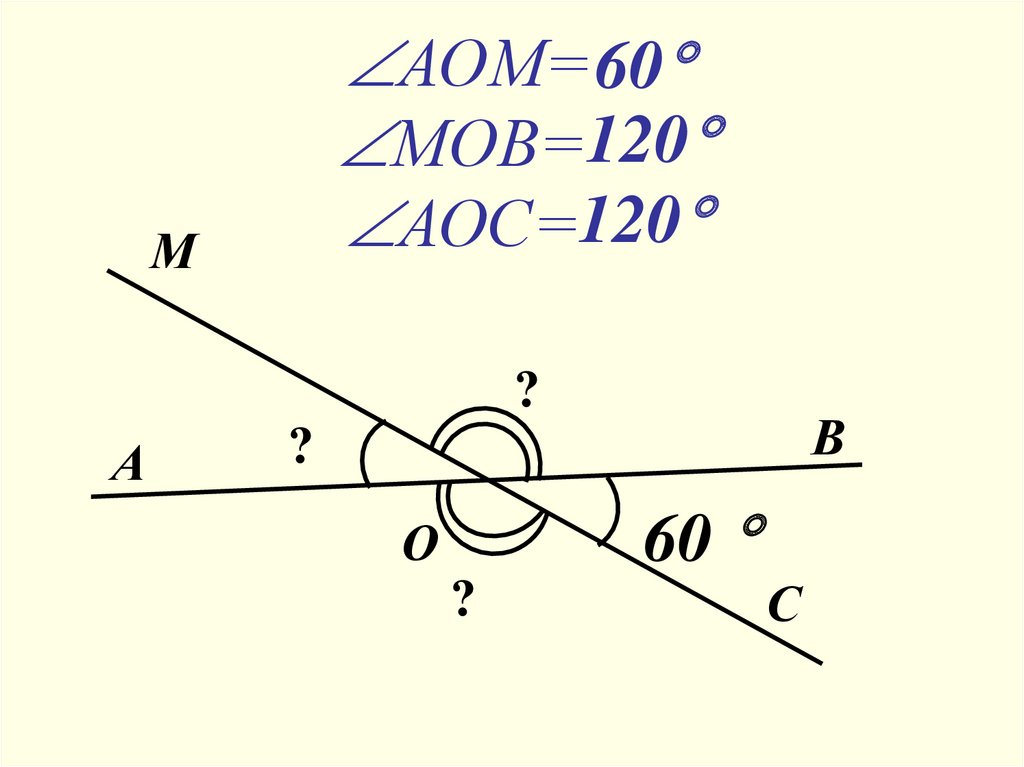
5.
АОМ= 60МОВ=120
АОС=120
М
?
А
В
?
60
О
?
С
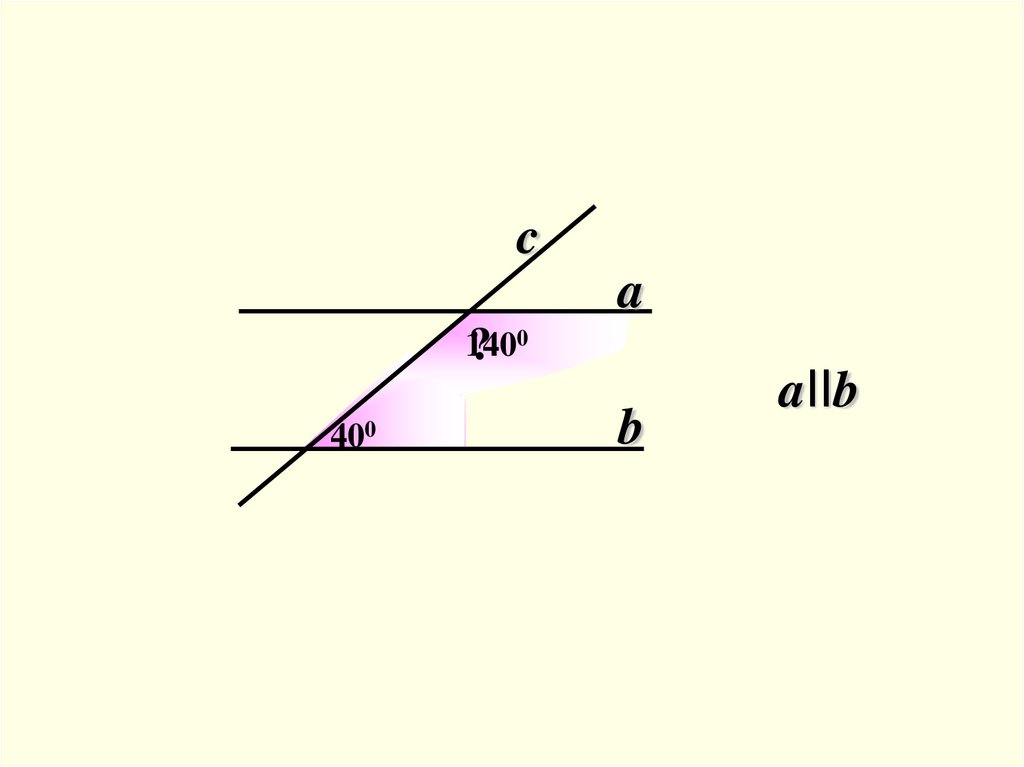
6.
ca
140
? 0
400
b
aIIb
7.
c45
?0
450
a
b
aIIb
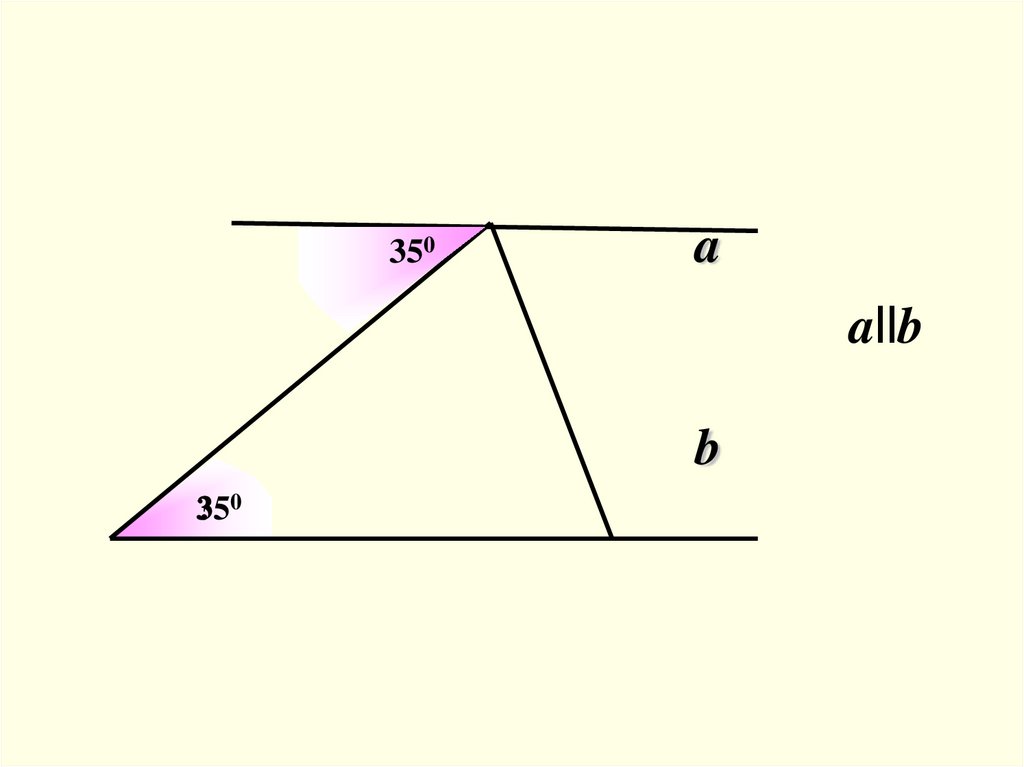
8.
350a
allb
b
?350
9.
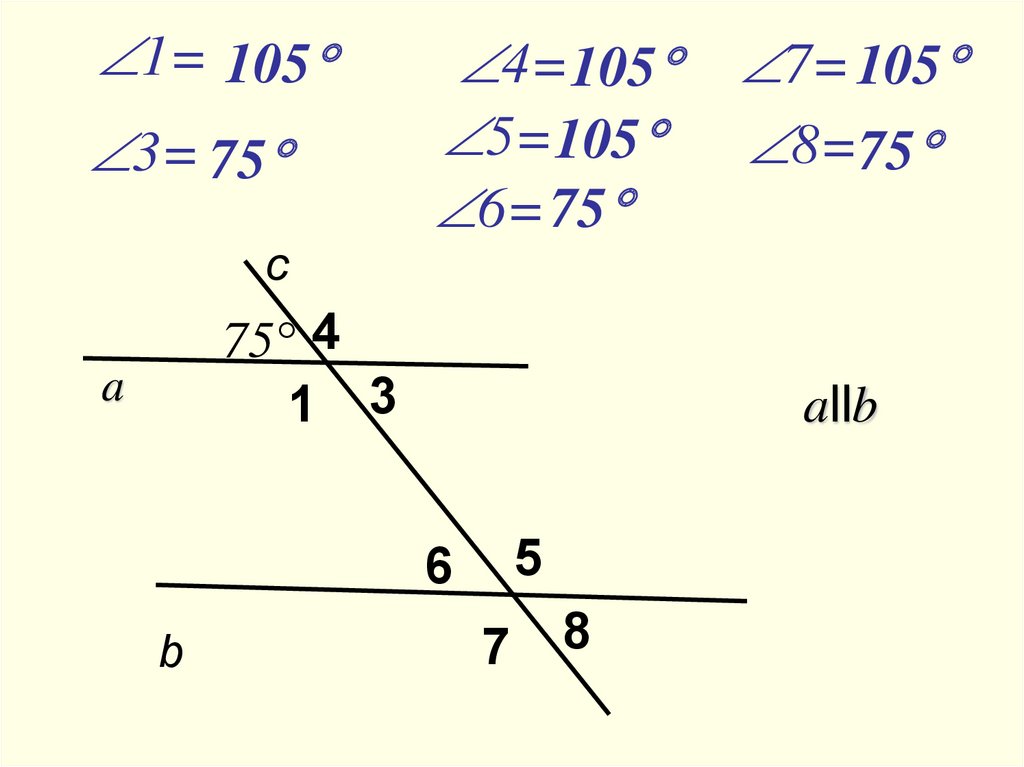
1= 1053= 75
4=105 7= 105
5=105 8=75
6= 75
c
75° 4
1 3
a
allb
5
6
b
7
8
10.
Теорема: Сумма угловтреугольника равна 180 .
11.
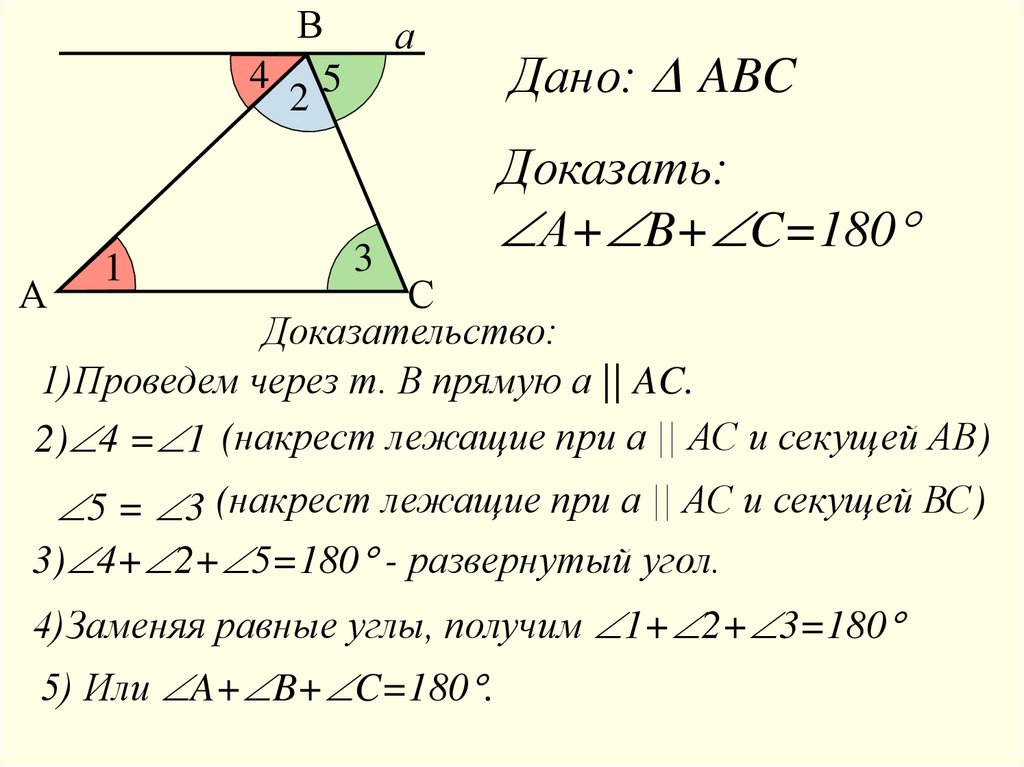
В4 5
2
А
1
а
3
Дано: ∆ ABC
Доказать:
А+ B+ C=180
С
Доказательство:
1)Проведем через т. В прямую а || AC.
2) 4 = 1 (накрест лежащие при а || АС и секущей АВ)
5 = 3 (накрест лежащие при а || АС и секущей ВС)
3) 4+ 2+ 5=180 - развернутый угол.
4)Заменяя равные углы, получим 1+ 2+ 3=180
5) Или A+ B+ C=180 .
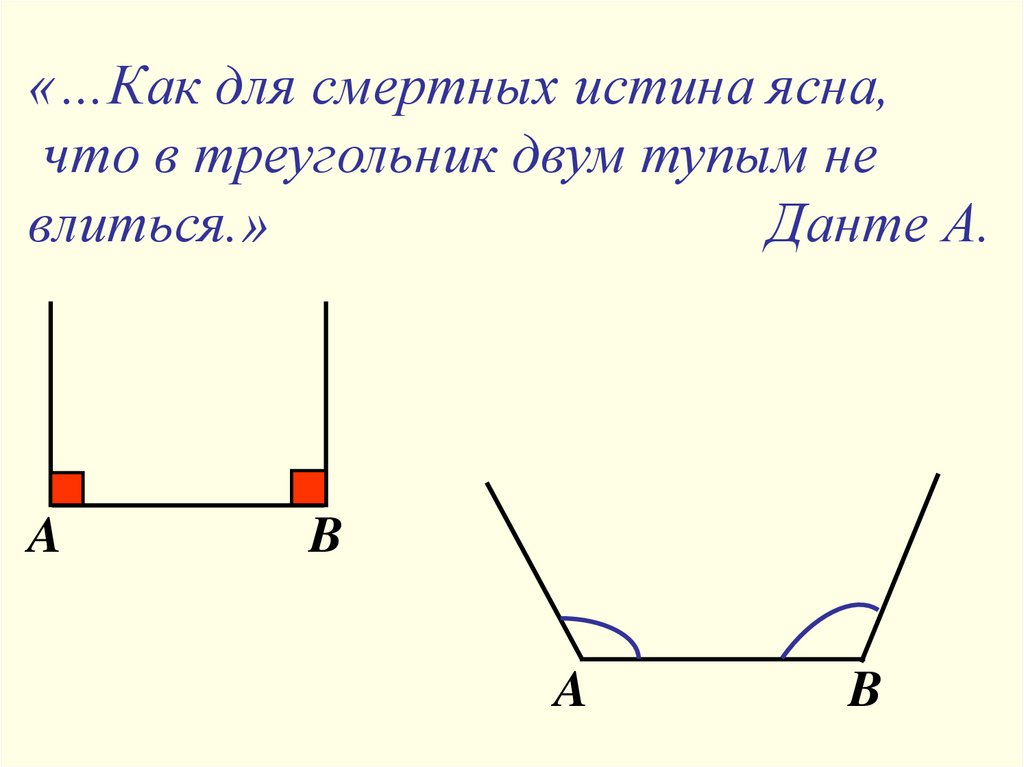
12.
«…Как для смертных истина ясна,что в треугольник двум тупым не
влиться.»
Данте А.
A
B
A
B
13. Пифагор
580 – 500 г.г. до н. э.Доказательство
теоремы о сумме углов
треугольника «Сумма
внутренних углов
треугольника равна
двум прямым»
приписывают
Пифагору .
14.
Евклид365 –300 г.г. до н.э.
В первой книге
«Начал» Евклид
излагает другое
доказательство
теоремы о сумме
углов треугольника,
которое легко
понять при помощи
чертежа.
15. Физкультминутка
Раз – согнуться, разогнуться,Два – нагнуться, подтянуться,
Три – в ладоши три хлопка,
Головою три кивка,
На четыре – руки шире,
На пять, шесть – тихо сесть,
На семь, восемь – лень отбросим,
И продолжим наш урок.
16. Задачи на готовых чертежах.
17.
Задача № 1В
350
А
750
C= 70
?
С
18.
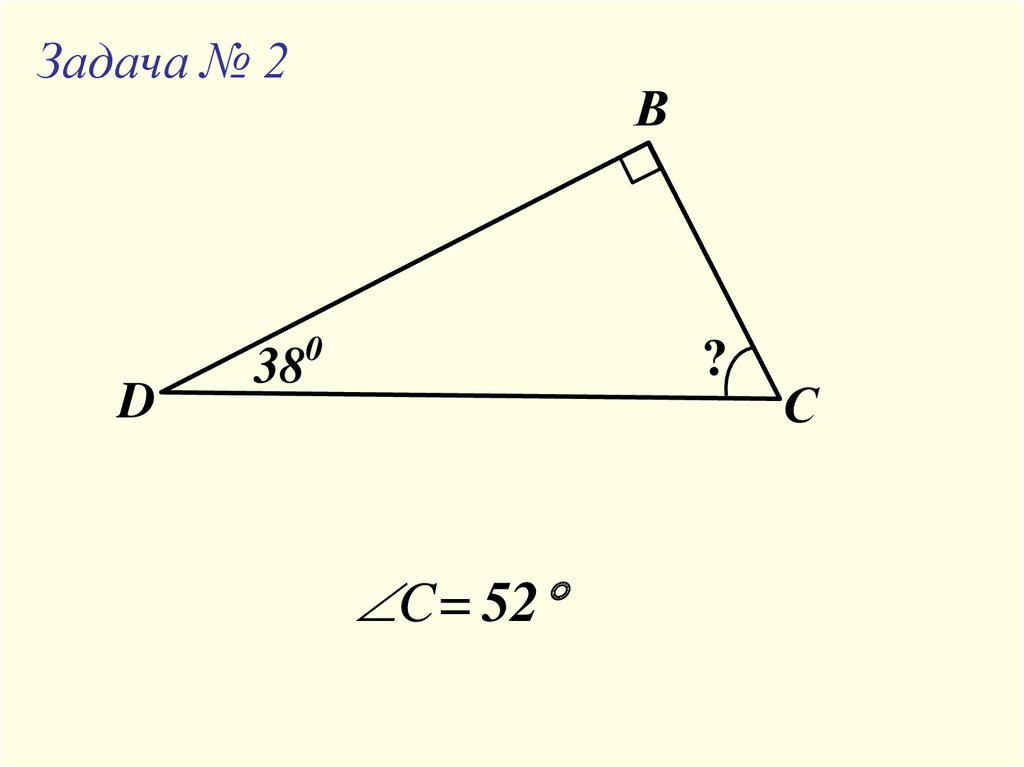
Задача № 2В
0
D
?
38
C= 52
С
19.
Задача № 3В
300
А
?
А= 80
1100
С
D
20.
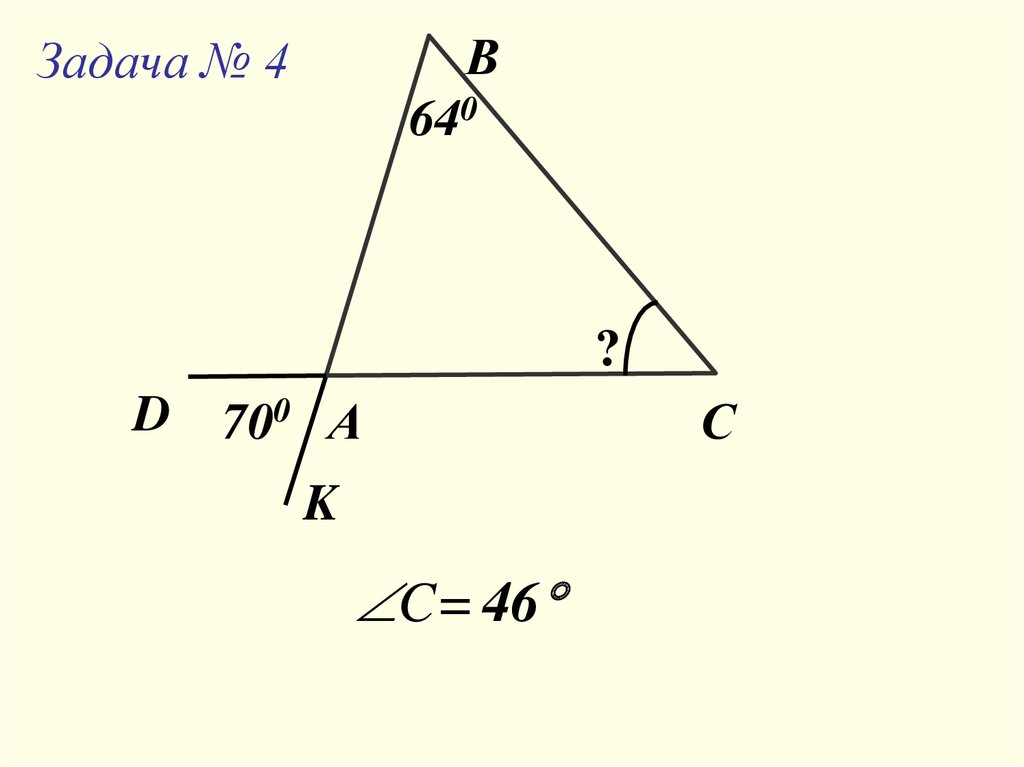
ВЗадача № 4
640
?
D
700 А
K
C= 46
С
21.
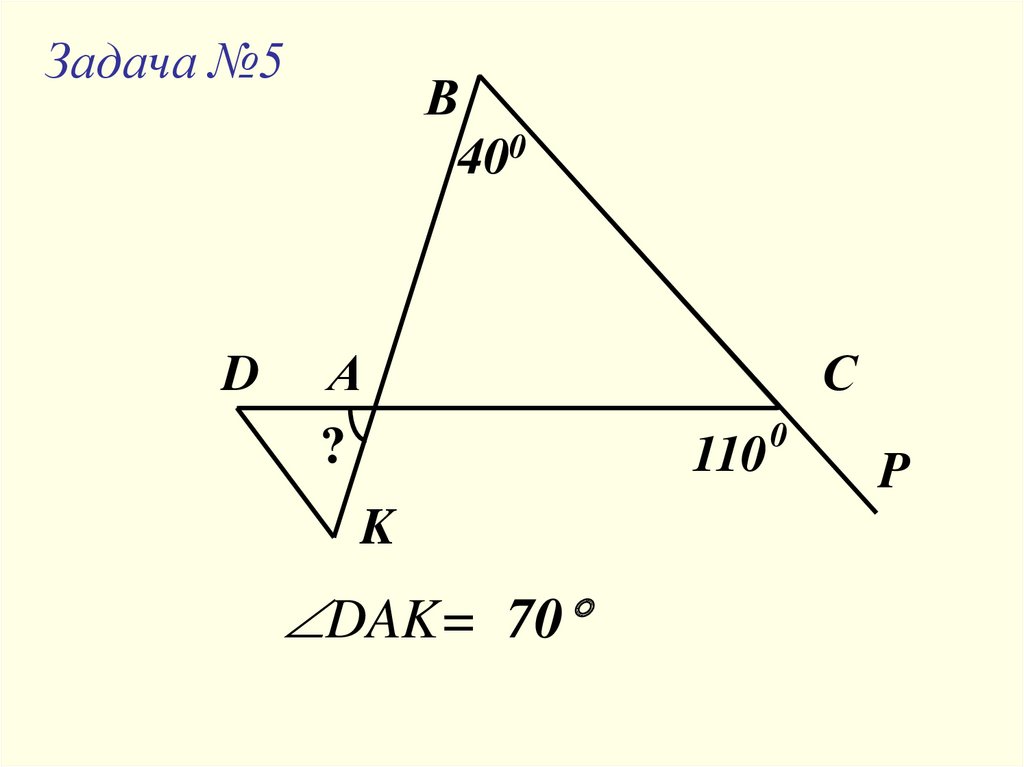
Задача №5D
В
400
А
?
K
DAK= 70
С
110
0
P
22.
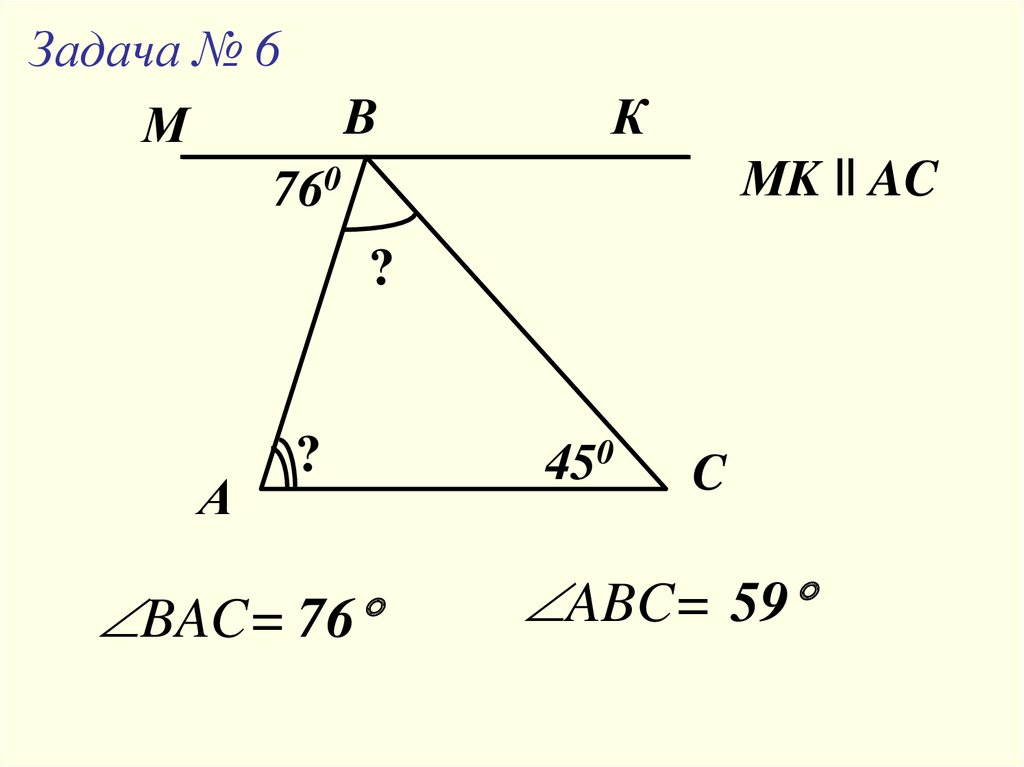
Задача № 6B
М
760
К
МK ll AC
?
А
?
BAC= 76
450
C
ABC= 59
23. Откроем учебник на странице 71, упражнение № 225
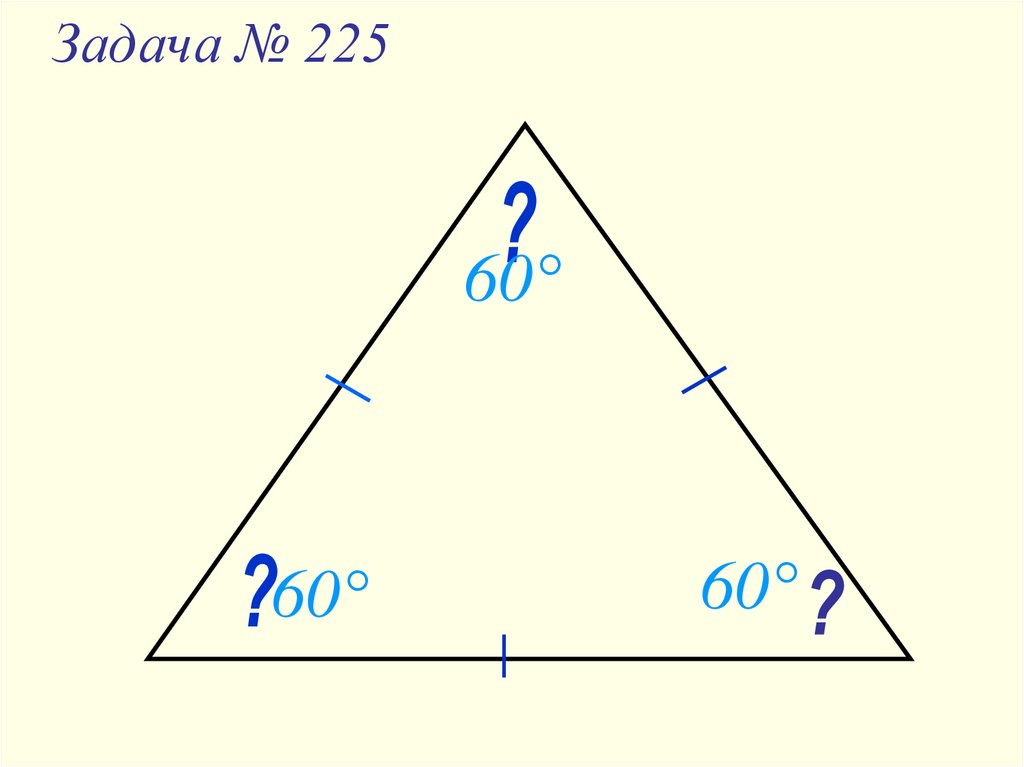
24. Задача № 225
60°60°
60°
25. Задача №228 (а)
1 случай2 случай
100
40
70
0
0
40
70
0
0
0
40
0
26. Подведем итог
• Какую мы сегодня изучали теорему?• Было ли на уроке легко, интересно?
• Оцените своё настроение на уроке:
хорошее равнодушное
плохое
27. Домашнее задание.
• § 30, 223(а, б), 228(в)• №229 (по желанию)
• Индивидуально карточки (по
желанию)
28.
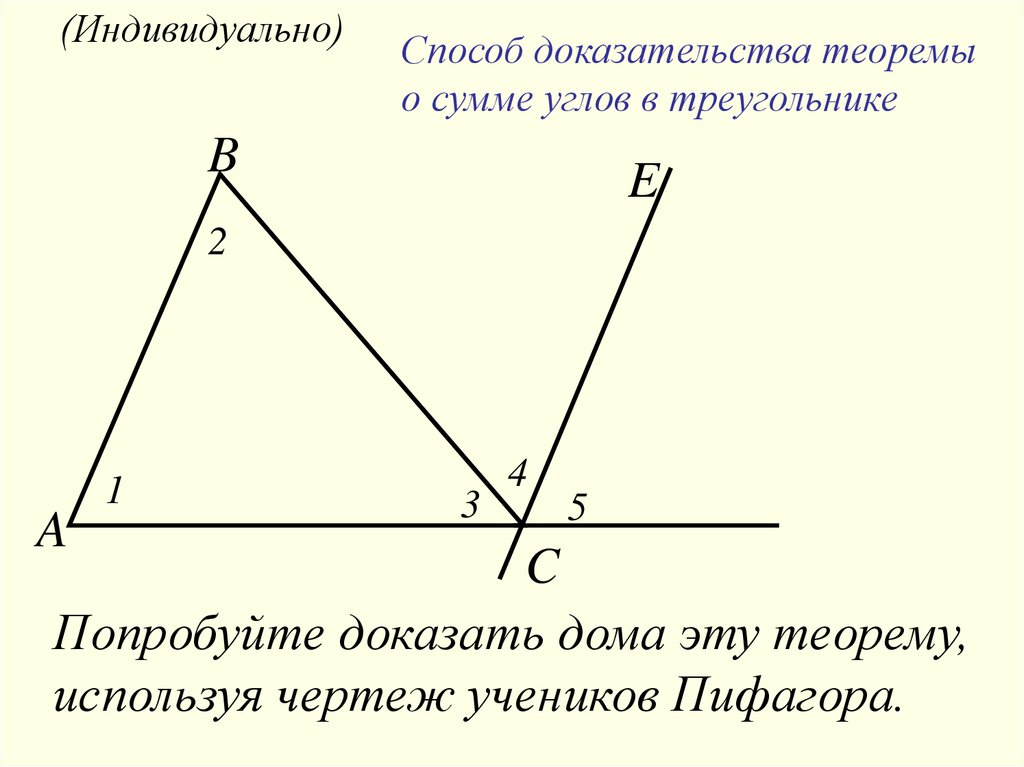
(Индивидуально)Способ доказательства теоремы
о сумме углов в треугольнике
B
E
2
A
1
3
4
5
C
Попробуйте доказать дома эту теорему,
используя чертеж учеников Пифагора.















 Математика
Математика








