Похожие презентации:
Радианная мера угла
1. Радианная мера угла
2.
π3
2
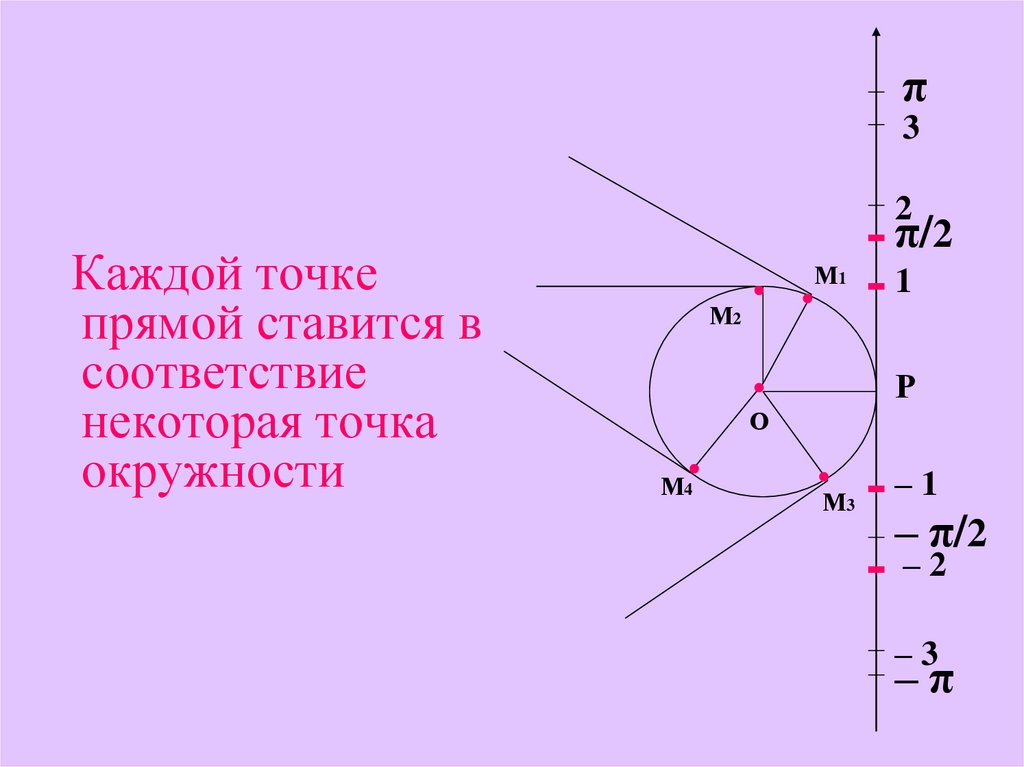
Каждой точке
прямой ставится в
соответствие
некоторая точка
окружности
π/2
М1
1
М2
Р
О
М4
М3
–1
– π/2
–2
–3
–π
3.
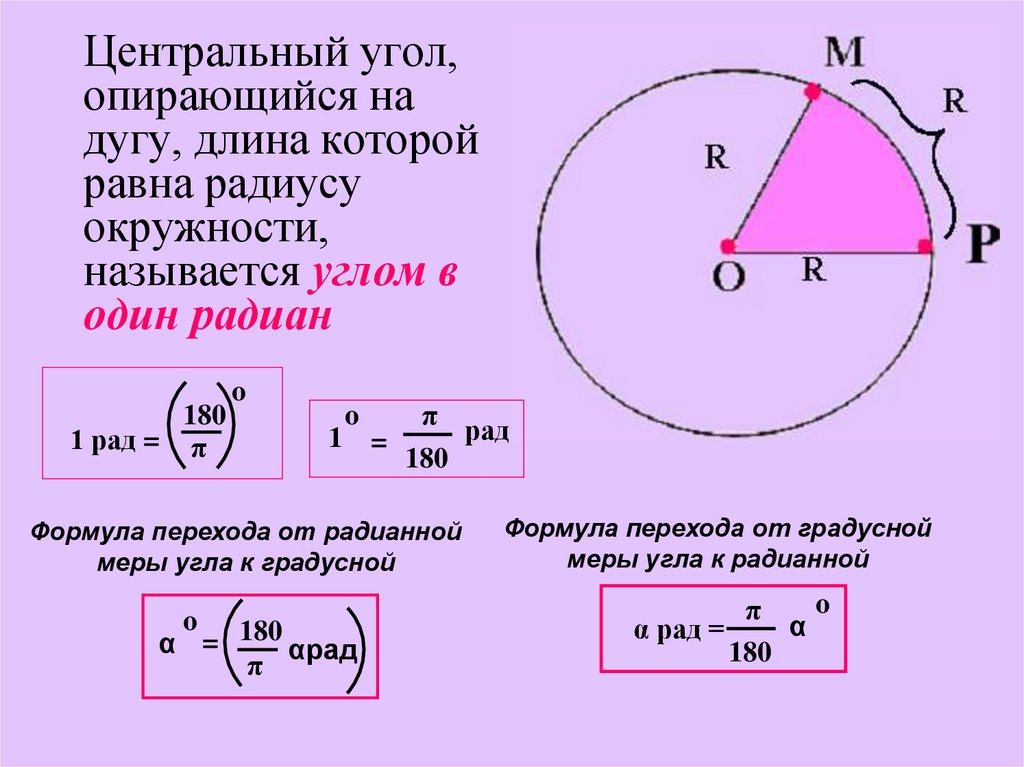
Центральный угол,опирающийся на
дугу, длина которой
равна радиусу
окружности,
называется углом в
один радиан
180
1 рад = π
o
π
рад
1 =
180
o
Формула перехода от радианной
меры угла к градусной
o
α = 180 αрад
π
Формула перехода от градусной
меры угла к радианной
o
π
α
α рад =
180
4.
Длина дуги:l = αR
Если α = 1 рад, то l = R
Площадь кругового сектора:
2
R α , где 0 < α < π
S=
2
5. Единичная окружность. Поворот точки вокруг начала координат
6.
Окружность с центром в начале координат и радиусомравным 1 называется единичной окружностью.
Уравнение единичной окружности имеет вид x2 + y2 =1
y
1
-1
1
0
x
-1
7.
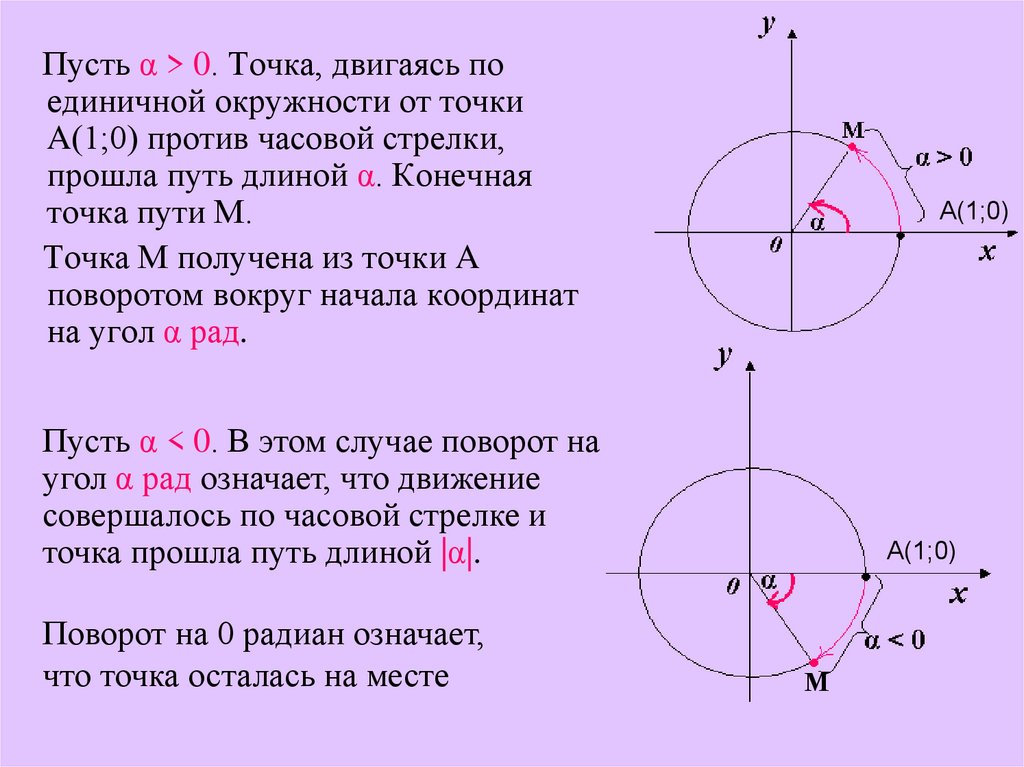
Пусть α > 0. Точка, двигаясь поединичной окружности от точки
A(1;0) против часовой стрелки,
прошла путь длиной α. Конечная
точка пути М.
Точка М получена из точки A
поворотом вокруг начала координат
на угол α рад.
A(1;0)
Пусть α < 0. В этом случае поворот на
угол α рад означает, что движение
совершалось по часовой стрелке и
точка прошла путь длиной |α|.
Поворот на 0 радиан означает,
что точка осталась на месте
A(1;0)
М
8. Четверти единичной окружности
I четвертьII четверть
III четверть
IV четверть
0<α<π/2
π/2<α<π
π<α<3π/2
3π/2<α<2π
y
π/2
II
I
π
0
III
0
IV
3π/2
2π
x
9.
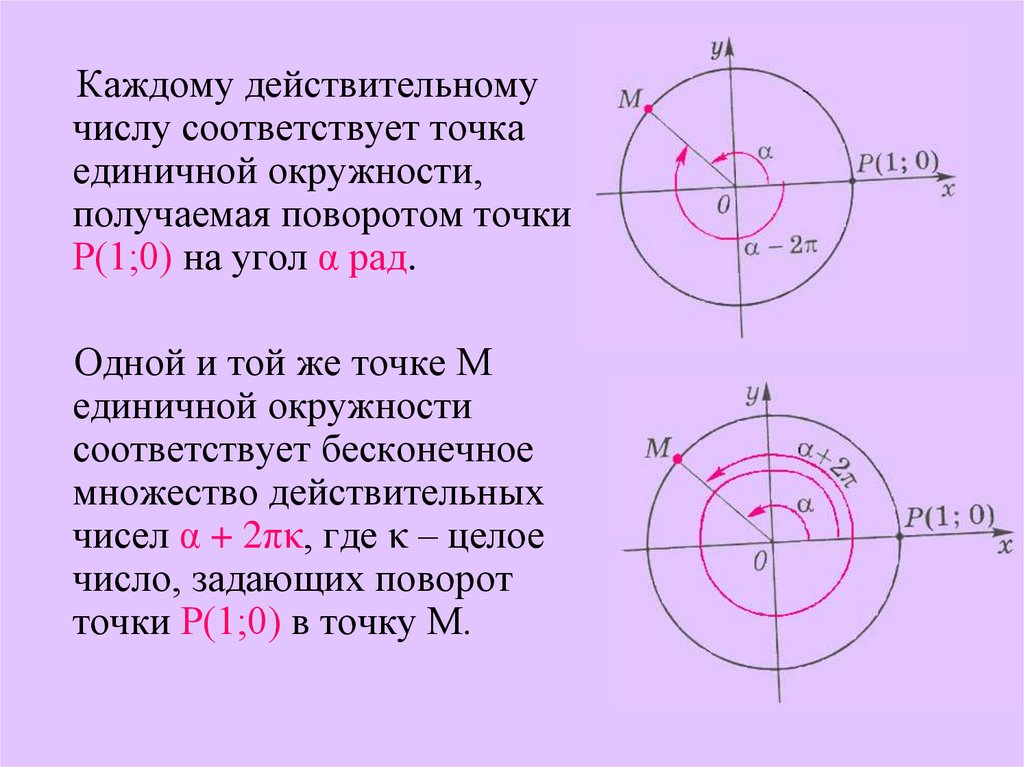
Каждому действительномучислу соответствует точка
единичной окружности,
получаемая поворотом точки
Р(1;0) на угол α рад.
Одной и той же точке М
единичной окружности
соответствует бесконечное
множество действительных
чисел α + 2πκ, где κ – целое
число, задающих поворот
точки Р(1;0) в точку М.
10. Определение синуса, косинуса и тангенса угла.
11.
Синусом угла α называется ордината точки, полученнаяповоротом точки (1;0) вокруг начала координат на угол α.
Обозначается sin α.
Косинусом угла α называется абсцисса точки, полученная
поворотом точки (1;0) вокруг начала координат на угол α.
Обозначается cos α.
Тангенсом угла α называется отношение синуса угла к его
косинусу. Обозначается tg α.
Котангенсом угла α называется отношение косинуса
угла к его синусу. Обозначается сtg α.
sin α
tg α =
cos α
cos α
ctg α = sin α
12.
Знаки синуса, косинуса,тангенса и котангенса
угла.
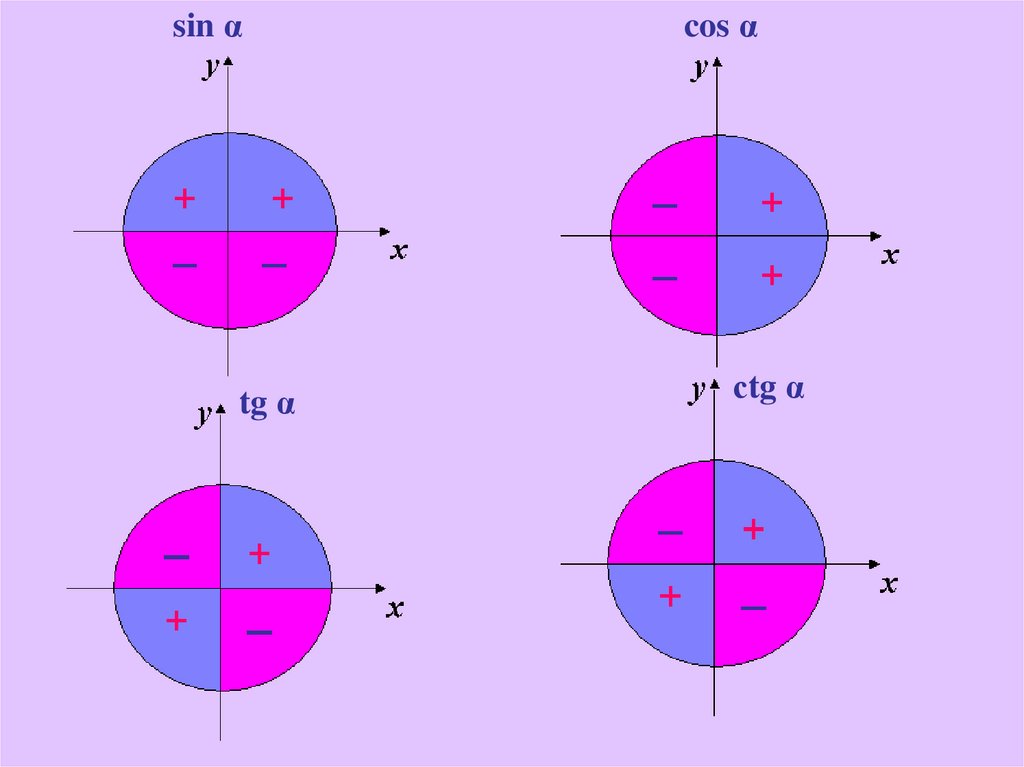
13.
sin αtg α
cos α
сtg α
14.
Синус, косинус,тангенс и котангенсуглов α и – α.
sin(– α) = – sin α
cos(– α) = cos α
tg(– α) = – tg α
ctg(– α) = – ctg α









 Математика
Математика








